基于物質點法的彈體侵徹靶板破甲特性數值模擬

秦業志，姚熊亮，王志凱，王瑩

哈爾濱工程大學 船舶工程學院，黑龍江哈爾濱150001

0 引 言

現代海戰中，艦船結構在遭受魚雷、反艦導彈等接觸攻擊時，在彈體的穿甲作用下易造成板殼結構的毀傷。艦船殼板穿甲過程是一個非線性、高瞬態的過程，它涉及到了材料大變形表現出的物理非線性、結構接觸、材料摩擦等問題，因此具有一定的復雜性［1］。艦船板殼結構穿甲研究的方法通常采用理論研究、實驗和數值模擬等方法。隨著計算機技術的飛速發展，計算成本日益降低，數值算法日臻成熟，使數值模擬成為研究穿甲問題時采用的主要方法。

目前，數值模擬船殼板結構穿甲過程的主要方法為有限元法和無網格法。基于拉格朗日描述的有限元方法是將網格附著在材料上，隨著材料的變形，網格也隨之變形，其基本思想是將函數定義在簡單的幾何形狀的單元域上，通過插值函數計算單元場內函數的近似解，從而得到整個求解域內的近似解。對于用有限元法處理彈體高速侵徹靶板的問題，材料發生大變形，單元容易產生嚴重的畸變，造成計算精度下降，甚至是導致計算中止。可見，對于極端大變形的問題，有限元法存在缺陷，特別是在模擬彈體侵徹靶板的過程中不能很好地模擬靶板破口的形態及動態形成過程。而無網格法在處理大變形問題時則體現出了優勢。

最初，人們普遍認為無網格方法是上世紀70年代提出的光滑粒子流體動力學（Smoothed Particle Hydrodynamic，SPH）方法。SPH方法當時主要用于研究天體物理學問題，經過幾十年的發展，已被廣泛應用于爆炸與沖擊動力學、水動力學、流體碰撞霧化等領域，且取得了顯著的研究成果［2］。此后，無網格法的研究得到了國內外學者的廣泛關注，提出了許多新的無網格法。典型的無網格法包括多種方法，如伽遼金型無網格法、配點型無網格法、基于局部弱形式和邊界積分方程的無網格法、最小二乘法和物質點法（Material Point Method，MPM）［3-4］。1994年，Sulsky等［5-6］將質點網格（Particle-in-cell）方法應用到了固體力學問題的研究中，并對數值方法進行了改進，由此提出MPM法。如今，該方法已成功應用于材料破壞、碰撞沖擊、生物力學等問題的研究，尤其是在處理材料破壞及材料大變形的問題時具有很大的優勢。MPM法是一種質點類無網格方法，它將連續體離散成一組攜帶有所有物質信息的物質點，通過物質點的運動表示物體的變形。同時，將物質點固聯到背景網格上，背景網格可以固定或自由布置，從而用于動量方程的求解和空間導數的計算。在求解過程中，物質點和網格點沒有相對運動，避免了歐拉法因非線性對流項產生的數值困難，并且極易跟蹤到物質界面。而在下一時間步中，仍采用未變形的背景網格，拋棄變形后的背景網格，因此避免了拉格朗日法因網格畸變而產生的數值困難。MPM法發揮了拉格朗日方法和歐拉方法各自的優點，非常適合用于分析超高速碰撞、侵徹等問題。例如，Lian等［7］運用MPM法成功模擬了鎢彈侵徹鋼靶等問題。Ma等［8］基于局部多重背景網格的物質點算法模擬了中、低速侵徹問題。馬上等［9］運用MPM法研究了彈丸高速碰撞板的一系列問題。

本文針對彈體侵徹船用鋼板的破甲特性，將重點研究靶板破壞形成的動態過程以及靶板的破壞形式，采用MPM法研究得到與實驗結果吻合較好的數值仿真結果，以驗證MPM法的有效性，從而為研究彈體侵徹船用鋼板材料的破甲問題提供新的研究途徑。

1 物質點算法

1.1 控制方程及物質點離散

本文不考慮熱效應，更新拉格朗日格式的控制方程如下［10-11］。

質量守恒方程：

式中：為現時構形物體的密度；為雅克比行列式；為物體初始時刻的密度。

動量守恒方程：

式中：σij為柯西應力張量，其中i，j為空間坐標的分量；ρ為當前時刻的密度；bi為作用在物體單位質量上的體力；為在i方向的加速度。

能量守恒方程：

式中：?為單位質量的內能；Dij為變形率張量。

本構關系：

式中：σ?為焦曼應力率。

幾何方程：

式中：為應變率；vi，j和vj，i為質點在空間坐標i，j方向的速度分量。

邊界條件：

式中:nj為材料邊界的單位法線方向；Γt和Γv分別為現時構形中指定的面力邊界和速度邊界為質點在i方向的速度；分別為指定的面力和速度。

初始條件：

式中為質點在i方向的位移；為質點在i方向的速度為質點在i方向的初始位移；為質點在i方向的初始速度。

MPM法將連續體離散成一組質點，如圖1所示。圖中，V為材料體積域，Vp為質點的體積域，Γ為構形中的指定邊界。每個質點代表一塊材料區域，同時攜帶物質信息，包括質量、速度、應力和應變等。物質點固連在背景網格內，背景網格用于計算空間導數及求解物體運動。

因此，離散連續體的密度ρ(xi)可以近似表示為

式中：np為質點總數；mp為質點p的質量；δ為Dirac Delta函數；xi為質量的坐標；xip為質點p的坐標。

在求解動量方程時，物質點和背景網格完全固連，并隨網格一起運動，因此，可建立背景網格結點上的有限元形函數NI(xi)來實現物質點和背景網格結點坐標之間信息的映射關系，如式（9）所示［12］。其中，帶下標I，J的量表示該網格結點變量，帶下標p的量表示質點攜帶的變量物質點和該網格結點坐標之間的映射關系，即

式中：為網絡結點I的形函數在質點處的值；uiI為結點I在i方向上的位移。

背景網格結點的運動方程為

背景網格結點I的內力為

式中：σijp為質點的柯西應力張量。

背景網格結點I的外力為

式中，h0為假想邊界層的厚度。

1.2 MPM求解方法

MPM法的求解有不同的實現格式，Sulsky和Bardenhagen等［5，13］討論了 2 種更新的應力求解格式 ，即 USF（Update Stress First）和 USL（Update Stress Last）格式。質點上的應變率是基于更新后的網格結點速度得到。此外，有人提出了一種改進的USL格式，即MUSL（Modified Update Stress Last）格式，并得到了廣泛應用，如下式［14］。

式中：NpI，i和NpI，j分別為網格節點I的形函數在質點處i，j方向的值；vIi，vIj分別為網格結點I在i，j方向的速度。上標n，n+1/2分別表示tn，tn+1/2時刻。

根據網格結點速度計算方法的不同，得到不同的求解格式如下：

1）USF格式。首先在每個時間步計算應變率，然后更新應變率，利用更新前的結點動量計算結點速度，最后代入式（15）得到應變率

2）USL格式。直接用網格結點動量來計算結點速度，即

式中，為網格結點I在i方向n時刻的動量。

3）MUSL格式。將更新后的網格結點動量映射到背景網格后再次計算結點的速度，

式中，vp i為質點在i方向的速度.

在本文研究中，采用MUSL格式的求解方法。

1.3 材料本構模型及物態方程

彈體和靶板的材料分別為D6A鋼和船用外殼921鋼，它們均采用Johnson-Cook本構模型，而狀態方程則采用Mie-Grunesien狀態方程。D6A鋼的層裂強度取為7.68 GPa，921鋼的層裂強度取為 6.24 GPa［15］。

Johnson-Cook本構模型屈服應力表達式為

式中：σ0為靜態屈服強度；B0和n為應變硬化參數；C為應變強化參數；m為熱軟化參數；εe為等效塑性應變；為等效塑性應變率；為參考應變率；T*為無量綱溫度，且，其中Tm為熔點溫度，Tr為室溫，e為內能，e0為高能炸藥單位質量的內能，CV為比熱。

Mie-Grunesien狀態方程表達式為

式中：γ為Gruneisen常數；PH為沖擊Hugoniot曲線上點的壓力；ξ為爆轟產物中的相對比容。

此刻，盜走尸體的這只山精，體型粗壯，比成人還要高著一頭，一身漆黑油亮的毛，蓬松而茂密，一看便是一只正處壯年的雄性山精。

彈體和靶板的具體參數［16］如表1所示。

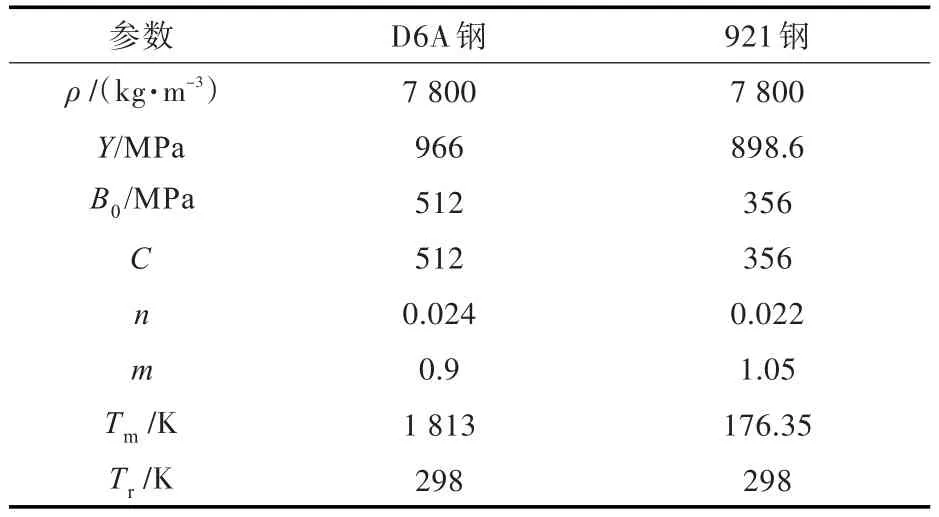
表1 材料模型參數Table 1 The parameters of material model

2 物質點法驗證

本文研究的彈體采用實心球頭，直徑為25 mm，球頭半徑為12.5 mm，彈體靶前速度V0=280 m/s，如圖2所示。彈體所用材料為硬度很高的D6A特種鋼，通常用于彈體的制造。靶板尺寸為400 mm×400 mm×5 mm，材料為應變率敏感的921鋼。

模擬中，彈體以V0=280 m/s的速度沖擊靶板，隨后靶板產生塑性大變形，彈體速度隨著時間的增加而減小，穿過靶板后，彈體以穩定的速度向前運動，并最終衰減為靶后速度V1=185 m/s，其與實驗結果相差不大。圖3所示為彈體侵徹靶板各時刻的破壞情況。圖4所示為彈體穿透靶板后的變形狀態。圖5所示為靶板背面的破口變形狀態。

由圖3～圖5可以看出，彈體以V0=280 m/s的速度沖擊靶板，靶板產生沖塞破壞，且隨著時間的增加，靶板產生的塑性變形增大，靶板材料受到嚴重的擠壓，產生大的變形，形成盤形凹陷。隨著彈體的繼續運動，靶板材料在運動方向上持續變形，當靶板材料隆起的塑性變形達到一定程度后，斷裂形成的沖塞體從靶體中飛離，沿著穿透方向繼續向前運動。當彈體穿透靶板后，靶板面上形成一個近似圓形的靶孔，其直徑與彈體直徑相近。表2所示為采用MPM法和實驗方法得到的彈體沖擊靶板過程中的結果，由表2可知兩種結果比較接近，相對誤差小于6%。

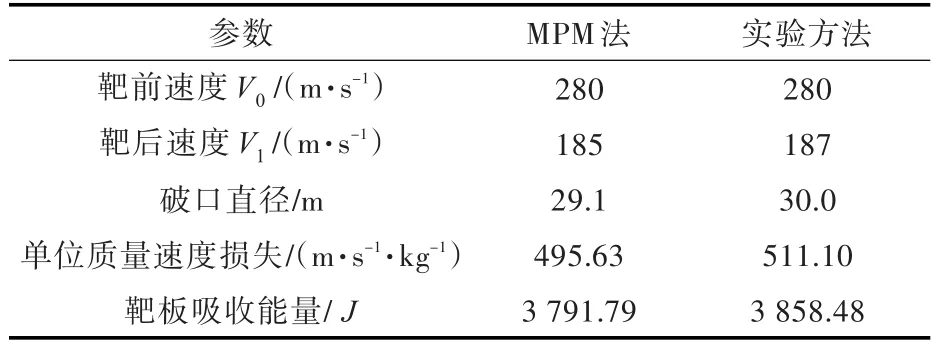
表2 彈體侵徹靶板的MPM法和實驗結果比較Table 2 Comparison of results acquired by MPM and experiment when the projectile penetrating target plate

3 彈體侵徹靶板數值模擬結果分析

本文基于建立的數值仿真模型，研究了彈體以不同靶前速度分別侵徹5和10 mm厚靶板時的破甲特性，并運用MPM法對彈體侵徹靶板的過程進行了仿真。彈體侵徹后靶板的破壞形態如圖6和圖7所示。

對于研究彈體侵徹靶板的問題，重點關注了靶板破口直徑和彈體剩余速度（即靶后速度）。由圖8、圖9以及表3可知：當彈體從中、高速和超高速狀態沖擊靶板時，靶板破口在26～35 mm之間；對于5 mm厚靶板的破壞形態，彈體速度越高，靶板破口直徑越小；在高速、超高速沖擊狀態下，靶板破口幾乎與彈體直徑相同，隨著彈體初速的增加，靶板沖塞破口隆起的高度也隨之增大，但彈體自身幾乎未發生變形；當靶板厚度為10 mm時，靶板破口直徑同樣略大于彈體直徑，隨著彈體速度的增加，靶板隆起高度的規律與薄板一樣，即隆起高度減小，但其明顯的區別是彈體頭部出現了變形。當撞擊厚板時，彈體頭部形狀發生變形，而侵徹靶板時彈體幾乎不發生變形。在同樣的侵徹速度下，侵徹厚板比侵徹薄板產生的破口隆起的高度要小，厚板的破口半徑略小于薄板，侵徹厚板的彈體變形比侵徹薄板的變形要大。對于彈體侵徹靶板，靶板越厚，彈體減小的速度幅度越大，消耗的能量就越多，故板厚影響了彈體最終的剩余速度，這一結論對于研究彈體侵徹多層靶板具有參考意義［17］。

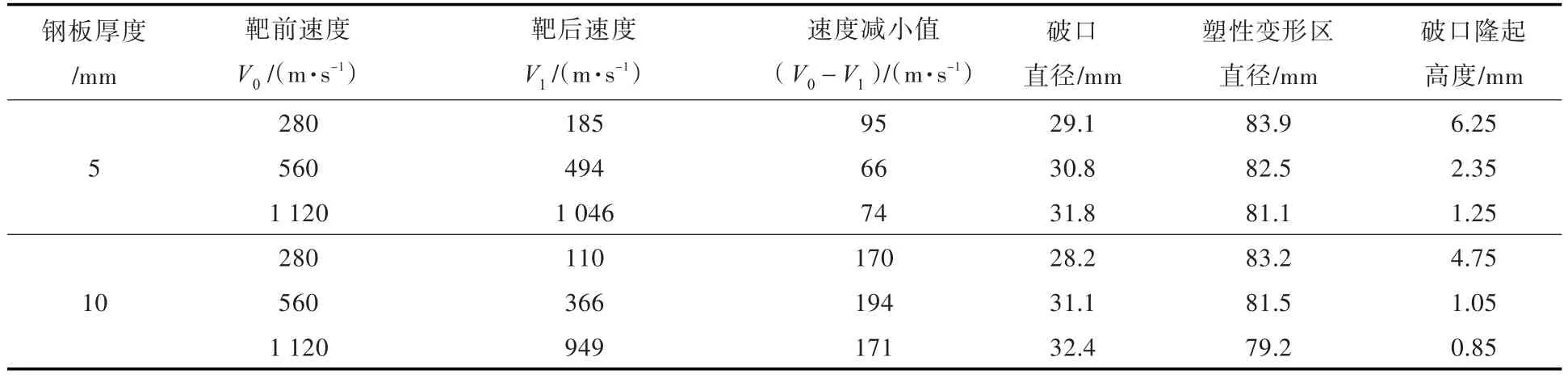
表3 彈體侵徹靶板的仿真結果比較Table3 Simulaiton results comparison of the projectile penetrating target plate

4 結 論

本文根據MPM法在模擬超高速碰撞方面的優勢，特別是能夠較好地模擬靶板破口的形成過程，建立了導彈侵徹艦船典型的板殼結構數值模型，仿真結果驗證了MPM法的有效性。在此基礎上，用該數值方法研究了彈體速度變化和靶板板厚變化下的破壞形態，得出如下結論：

1）MPM法數值模擬結果與實驗結果吻合較好，說明采用MPM法模擬船體板殼穿甲問題完全可行。對于艦船板殼結構受到彈體沖擊的大變形問題，MPM法不僅可以模擬靶板材料的破壞形式，還可以對材料的破壞程度進行評估，故是一種研究艦船板殼結構穿甲問題的新的有效方法。

2）以25 mm直徑彈體為例，模擬其以不同速度侵徹5和10 mm厚靶板，得到靶板破口直徑在26～29.5 mm之間，塑性變形區的范圍大小幾乎不變，約30 mm；彈體速度對靶板破口的影響很小，但對靶板沖塞破口隆起的高度影響較大；彈體速度越高，靶板越厚，彈體頭部更會產生變形。彈體侵徹靶板的破壞屬于沖塞穿甲形式，符合實驗研究的規律。

3）本文建立的數值模型能夠很好地模擬彈體侵徹靶板的破壞形成過程，相對誤差小于6%，模擬精確度高，所以本方法具有可行性，數值模擬結果可用于指導實驗設計，并為艦船橫艙壁防護設計提供參考。

［1］寧建國，王成，馬天寶.爆炸與沖擊動力學［M］.北京：國防工業出版社，2010.

［2］LUCY L B.A numerical approach to the testing of the fission hypothesis［J］.Astronomical Journal，1977，82（12）：1013-1024.

［3］張雄，劉巖.無網格法［M］.北京：清華大學出版社，2004：1-10.

［4］張雄，宋康祖，陸明萬.無網格法研究進展及其應用［J］.計算力學學報，2003，20（6）：730-741.ZHANG X，SONG K Z，LU M W.Research progress and application of meshless method［J］.Chinese Journal of Computational Mechanics， 2003， 20（6）：730-741（in Chinese）.

［5］SULSKY D，CHEN Z，SCHREYER H L.A particle method for history-dependent materials［J］.Computer Methodsin AppliedMechanicsandEngineering，1994，118（1/2）：179-196.

［6］SULSKY D，ZHOU S J，SCHREYER H L.Application of a particle-in-cell method to solid mechanics［J］.Computer Physics Communications，1995，87（1/2）：236-252.

［7］LIAN Y P，ZHANG X，LIU Y.Coupling of finite element method with material point method by local multi-mesh contact method［J］.Computer Methods in AppliedMechanicsandEngineering， 2011，200：3482-3494.

［8］MA Z T，ZHANG X，HUANG P.An object-oriented MPM framework for simulation of large deformation and contact of numerous grains［J］.CMES-Computer Modeling in Engineer&Science，2010，55（1）：61-87.

［9］馬上，張雄，邱信明.超高速碰撞問題的三維物質點法［J］.爆炸與沖擊，2006，26（3）：273-278.MA S，ZHANG X，QIU X M.Three-dimensional material point method for hypervelocity impact［J］.Explosion and Shock Waves，2006，26（3）：273-278（in Chinese）.

［10］周旭，張雄.物質點法數值仿真（軟件）系統及應用［M］.北京：國防工業出版社，2015：1-9.

［11］張雄，廉艷平，劉巖，等.物質點法［M］.北京：清華大學出版社，2003：15-27.

［12］馬上.沖擊爆炸問題的物質點無網格法研究［D］.北京：清華大學，2009.MA S.Material point meshfree methods for impact and explosion problems［D］.Beijing：Tsinghua University，2009（in Chinese）.

［13］BARDENHAGEN S G.Energy conservation error in the material point method for solid mechanics［J］.Journal of Comutational Physics，2002，180：383-403.

［14］廉艷平，張帆，劉巖，等.物質點法的理論和應用［J］. 力學進展，2013，43（2）：237-264.LIAN Y P，ZHANG F，LIU Y，et al.Material point method and its applications［J］.Advances in Mechanics，2013，43（2）：237-264（in Chinese）.

［15］張林，張祖根，秦曉云，等.D6A、921和45鋼的動態破壞與低壓沖擊特性［J］.高壓物理學報，2003，17（4）：305-310.ZHANG L，ZHANG Z G，QIN X Y，et al.Dynamic fracture and mechanical property of D6A，921 and 45 steels under low shock pressure［J］.Chinese Journal of High Pressure Physics，2003，17（4）：305-310（in Chinese）.

［16］許慶新.基于SPH方法的沖擊動力學若干問題研究［D］.上海：上海交通大學，2009.XU Q X.Study of some impact dynamics problems based on smoothed particle hydrodynamics method［D］. Shanghai： Shanghai Jiao Tong University，2009（in Chinese）.

［17］程素秋，陳高杰，趙紅光.聚能戰斗部對雙層靶板結構毀傷的數值模擬研究［J］.中國艦船研究，2013，8（2）：53-57.CHENG S Q，CHEN G J，ZHAO H G.Numerical damage analysis of shaped charge warheads on double-deck target plates［J］.Chinese Journal of Ship Research，2013，8（2）：53-57（in Chinese）.