改進的3階WENO-N3格式及其在內爆炸載荷計算中的應用

徐維錚 ，吳衛國

1武漢理工大學高性能艦船技術教育部重點實驗室，湖北 武漢 430063

2武漢理工大學交通學院，湖北 武漢 430063

0 引 言

高分辨率激波捕捉格式對含激波流場的數值模擬具有重要意義，其不但可以降低網格的規模，而且還能較好地分辨出流場中復雜的波系結構。Liu等［1］在本質無振蕩（ENO）概念［2］的基礎上提出WENO格式，將ENO格式改進為所有模板的加權平均，而權值則依據模板的光滑程度而定。Jiang等［3］通過引入新的光滑因子，構造了3階和5階WENO格式。

然而，Henrick等［4］指出傳統的 5階WENO格式在一階極值點處精度會降為3階。為了解決這個缺陷，采用映射函數法提出了5階精度的WENO-M格式。Borges等［5］則通過線性組合低階候選模板光滑因子構造全局高階光滑因子的方式，提出5階WENO-Z格式。之后，大量的研究［6-13］致力于改進高階WENO格式（主要集中在5階、7階和9階）在極值點處、間斷處附近的精度。針對3階WENO格式的改進，主要有以下幾種：Yamaleev等［14］提出的能量穩定 ESWENO，Wu等［15-16］提出的WENO-N3格式以及WENO-NP3格式。近期，Acker等［17］指出，增大非光滑模板所對應的非線性權重能夠改善格式的分辨率，并推導給出5階WENO-Z+格式，數值試驗表明，該格式具有比WENO-Z格式更小的耗散性。

本文將在文獻［15，17］所做工作的基礎上，提出改進格式WENO-N+3，并通過理論推導和數值算例的方式，驗證改進格式WENO-N+3相較WENO-JS3，WENO-Z3，WENO-N3格式所具有的特性。最后，將改進格式WENO-N+3應用于封閉空間內爆炸載荷的數值計算。

1 控制方程

含激波流場采用可壓縮歐拉方程進行描述，其三維形式［18］如下：

式中：ρ為密度；u，v，w為x，y，z方向上的速度分量；p為流體壓力；E為單位體積流體的總能量；e為比內能；γ為氣體的絕熱指數，在本文數值計算中取為1.4。

在式（1）的每個方向上均可以看成雙曲守恒律方程：

例如，針對x方向，式（5）的數值離散形式為

式 中 ：分別為單元（xi-1/2，xi+1/2）的左、右界面對流項數值通量；h為x方向的均勻網格間距，在本文的數值計算中，x，y，z方向的網格間距相同。控制方程的空間離散采用下述的數值方法，時間項離散采用3階TVD龍格庫塔格式［19］。

2 數值方法

2.1 3階WENO-JS格式數值重構過程

3階WENO格式（WENO-JS3）的數值離散和推導過程如下［3］，為了簡潔表述，僅給出了右界面通 量的重構過程，對于3階WENO格式，的2種重構方式分別為：

利用上述2種2階通量的加權組合計算最終具有3階精度的數值通量即

對于光滑情形，有式（8）給出的形式既適合光滑流場也適合含間斷流場，對于含激波的間斷流場，式中的非線性權函數ωk需要根據下式求得：

式中，參數ε取值為10-6。光滑因子βk(k=0，1)的表達式為

文獻［14，20］通過理論推導，給出3階WENO格式達到收斂精度的充分條件為

2.2 WENO-N3格式

3階 WENO-Z 格式［21］（WENO-Z3）的具體形式如下：

文獻［15］首先指出，傳統的3階WENO-Z格式在極值點處會降階，并提出了WENO-N3格式：

式中：τ，τN為高階全局光滑因子；β3表示3階WENO格式全局模板（xi-1，xi，xi+1）的光滑因子：

這里通過理論推導分析WENO-N3格式在1階極值點處的計算精度，當存在1階極值點時，β3在xi處泰勒級數展開為

式（10）中的光滑因子在xi處泰勒級數展開為

將式（17）～式（18）代入式（14）和式（15），可得

再根據加權法，則可得右界面通量所對應的權函數

同理，可得左界面通量所對應的權函數

式（21）和式（22）顯示，式（23）和式（24）顯示，均不滿足充分條件，因此，WENO-N3格式在光滑流場極值點處的精度將降低。文獻［15］中的極值點精度測試顯示，3階WENO-N3格式在1階極值點處將降低為1階精度。

2.3 改進的3階WENO-N3格式

文獻［17］表示，在相對稀疏的網格下，增大非光滑模板的非線性權重，相比單純提高格式在極值點處的精度，前者能給出分辨率更好的結果，在該構造思想的啟發下，直接給出了改進格式WENO-N+3：

式中，λ=h0=1，其取值依據3.2小節的算例分析。

2.3.1 構造原理證明

改進格式的構造思想是增大非光滑模板的非線性權重，從而降低格式的耗散性，提高格式的分辨率，以下給出基本證明［22］。

基本假定：3階WENO格式有2個子模板SC，SD，其中SC為光滑模板，SD為含間斷模板，意味著光滑因子βC＜βD。

證明：不考慮數值很小的參數ε，根據式（14）和式（25）可得

因為βD＞βC，令

將式（28）代入式（27），可得

根據式（27）和式（29），最終得證改進格式WENO-N+3相較WENO-N3格式增大了非光滑模板的非線性權重：

2.3.2 極值點處的精度

通過理論推導分析改進的WENO-N+3格式在1階極值點處的計算精度，通過系列推導，可得右界面通量所對應的權函數

同理，可得左界面通量所對應的權函數

根據式（31）～式（34）可知，不能滿足式（11）的充分條件，因此可以預知其在極值點處將降階。

3 數值驗證

為了進一步考察改進格式WENO-N+3的計算性能，選取線性精度測試、激波與熵波相互作用、雙爆轟波碰撞、瑞利—泰勒不穩定性等經典算例進行自主編程計算，并將該格式計算結果與格式WENO-JS3，WENO-Z3和WENO-N3進行對比分析。

3.1 精度測試

該算例選自文獻［4］，計算初始條件為

其包含2個1階極值點。表1給出了WENOJS3，WENO-Z3，WENO-N3和 WENO-N+3格式的L1范數來計算誤差和精度，其中N為網格數。可知，改進格式WENO-N+3，WENO-N3格式基本上具有相同的精度，在極值點處均沒有達到3階收斂精度，與2.2和2.3.1節的理論分析相一致。

3.2 激波與熵波相互作用

該算例初始條件［19］如式（36）所示，網格數為800，計算結束時間為1.8。圖1給出了計算結束時刻密度曲線圖及局部放大圖。

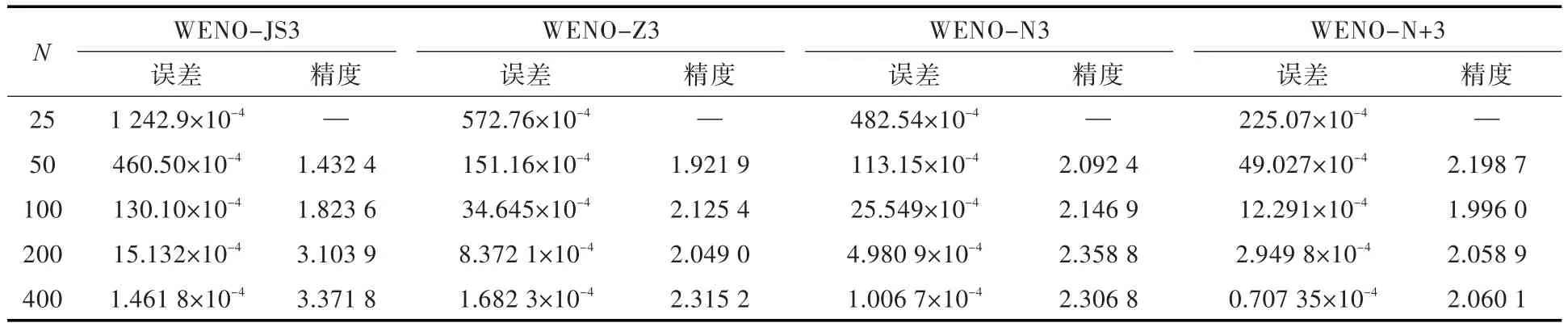
表1 針對初始條件，在結束時間為2時不同數值計算格式L1誤差和精度比較Table 1 A comparison study ofL1（error and order）for different schemes with initial condition at t=2

為了考察不同參數λ對改進格式WENO-N+3的影響規律，針對該算例，選用4個不同的數值：λ=h0，h1/2，h2/3，h3/3進行數值計算。圖2給出相應的計算結果。根據圖2發現，隨著參數λ的增大，格式給出了耗散更低的計算結果，其中參數λ=h0=1給出了較優的計算結果。由于WENO格式需要在激波附近具備一定的數值耗散以抑制數值振蕩，因此，過大的增加參數λ的數值將會造成一定的虛假振蕩。本文的數值計算結果表明，參數λ=h0=1是改進格式WENO-N+3綜合權衡耗散性和計算穩定性后較為折中的參數，這也是本文選取參數λ=h0=1的主要考慮。

3.3 爆轟波相互作用

該問題選自文獻［23］，其初始條件如式（37）所示：

計算網格數為800，計算結束時間為0.038，兩端邊界條件取為剛性反射邊界。

根據圖1和圖3中的一維算例結果可知，改進格式WENO-N+3相較于WENO-N3，WENO-Z3和WENO-JS3格式具有更低的耗散性。

3.4 瑞利—泰勒不穩定性

該問題主要描述重力場作用下，重流體加速進入輕流體界面失穩的過程。文獻［17，24-25］也采用該算例探討過數值方法的分辨率特性。計算域設置為［0，0.25］×［0，1］，計算初始條件如下所示：

該算例中，絕熱指數γ取值為5/3。在歐拉方程y方向的動量方程和能量方程右端分別加入ρ，ρv作為源項來考慮重力效應。左、右邊界設置成反射邊界條件，頂部和底部邊界條件分別為（ρ，u，v，p）=（1，0，0，2.5），（ρ，u，v，p）=（2，0，0，1）。網格數劃分為240×960，計算結束時間為1.95。

各格式（WENO-JS3，WENO-Z3，WENO-N3和WENO-N+3）的密度等值線圖如圖4所示，共繪制出15條等值線，其取值區間為［0.952 269，2.145 89］。改進格式WENO-N+3在接觸間斷附近具有更低的耗散性，能給出分辨率更清晰的計算結果。

4 三維封閉空間內爆炸

將改進格式WENO-N+3應用于正方體封閉空間內柱形炸藥爆炸載荷計算，并將計算結果與WENO-JS3，WENO-N3進行比較分析。

4.1 初始條件

封閉空間尺寸為800 mm×800 mm×800 mm，壁面上設置2個測點，分別編號為No.1和No.2，對爆炸超壓時間歷程進行輸出，如圖5（a）所示。

柱形炸藥位于中間，瞬時爆轟后的高壓、高密度氣體參數為：半徑50 mm，高度140 mm，密度1 630 kg/m3，壓力 3.057 9×109Pa。計算初始條件如圖5（b）所示，圖中P為爆炸壓力。網格數選取為40×40×40。壁面邊界條件設置為剛性反射邊界。

4.2 典型測點超壓對比

為了比較改進格式WENO-N+3與WENO-JS3，WENO-N3格式對于爆炸載荷計算的差異性，給出爆炸波演化過程（圖6），并對壁面2個典型測點No.1和No.2的超壓時間歷程曲線進行了對比分析。

三維封閉空間內部爆炸載荷由于爆炸波的壁面反射和疊加，呈現出不斷衰減的多峰值特點。從圖7的對比結果可以看出，改進格式WENO-N+3相較WENO-JS3和WENO-N3給出了較優的結果，尤其能以較低的耗散捕捉內爆炸載荷的前幾個峰值。

5 結 論

通過本文的研究，主要得到以下2點結論：

1）改進格式WENO-N+3相較其他格式（WENO-JS3，WENO-Z3，WENO-N3）具有較低的耗散，提高了對復雜流場結構的分辨率。

2）改進格式WENO-N+3在相同的計算網格下能給出較高的沖擊波峰值，其用于內爆炸載荷的數值計算具有一定的可行性。

［1］LIU X D，OSHER S，CHAN T.Weighted essentially non-oscillatory schemes［J］.Journal of Computational Physics，1994，115（1）：200-212.

［2］HARTEN A，ENGQUIST B，OSHER S，et al.Uniformly high order accurate essentially non-oscillatory schemes，III［J］.Journal of Computational Physics，1987，71（2）：231-303.

［3］JIANG G S，SHU C W.Efficient implementation of weighted ENO schemes［J］.Journal of Computational Physics，1995，126（1）：202-228.

［4］HENRICK A K，ASLAM T D，POWERS J M.Mapped weighted essentially non-oscillatory schemes：achieving optimal order near critical points［J］.Journal of Computational Physics，2005，207（2）：542-567.

［5］BORGES R，CARMONA M，COSTA B，et al.An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws［J］.Journal of Computational Physics，2008，227（6）：3191-3211.

［6］YAMALEEV N K，CARPENTER M H.A systematic methodology for constructing high-order energy stable WENO schemes［J］.Journal of Computational Physics，2009，228（1）：4248-4272.

［7］FAN P.High order weighted essentially nonoscillatory WENO-ηschemes for hyperbolic conservation laws［J］.Journal of Computational Physics，2014，269：355-385.

［8］FAN P，SHEN Y Q，TIAN B L，et al.A new smoothness indicator for improving the weighted essentially non-oscillatory scheme［J］.Journal of Computational Physics，2014，269：329-354.

［9］FENG H， HUANG C， WANG R.An improved mapped weighted essentially non-oscillatory scheme［J］.Applied Mathematics and Computation，2014，232：453-468.

［10］SHEN Y Q，ZHA G H.Improvement of weighted essentially non-oscillatory schemes near discontinuities［J］.Computers&Fluids，2014，96：1-9.

［11］KIM C H，HA Y，YOON J.Modified non-linear weights for fifth-order weighted essentially non-oscillatory schemes［J］.Journal of Scientific Computing，2016，67（1）：299-323.

［12］MA Y K，YAN Z G，ZHU H J.Improvement of multistep WENO scheme and its extension to higher orders of accuracy［J］.International Journal for Numerical Methods in Fluids，2016，82（12）：818-838.

［13］WANG R，FENG H，HUANG C.A New mapped weighted essentially non-oscillatory method using rational mapping function［J］.Journal of Scientific Computing，2016，67（2）：540-580.

［14］YAMALEEV N K，CARPENTER M H.Third-order energy stable WENO scheme［J］.Journal of Computational Physics，2013，228（8）：3025-3047.

［15］WU X S， ZHAO Y X.A high-resolution hybrid scheme for hyperbolic conservation laws［J］.International Journal for Numerical Methods in Fluids，2015，78（3）：162-187.

［16］WU X S，LIANG J H，ZHAO Y X.A new smoothness indicator for third-order WENO scheme［J］.International Journal for Numerical Methods in Fluids，2016，81（7）：451-459.

［17］ACKER F，DE R BORGES RB，COSTA B.An improved WENO-Z scheme［J］.Journal of Computational Physics，2016，313：726-753.

［18］TORO E F.Riemann solvers and numerical methods for fluid dynamics：a practical introduction［M］.Berlin Heidelberg：Springer，1999：87-114.

［19］SHU C W，OSHER S.Efficient implementation of essentially non-oscillatory shock-capturing schemes，II［J］.Journal of Computational Physics，1989，83（1）：32-78.

［20］GANDE N R，RATHOD Y，RATHAN S.Third-order WENO scheme with a new smoothness indicator［J］.International Journal for Numerical Methods in Fluids，2017，85（2）：90-112.

［21］DON W S，BORGES R.Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes［J］.Journal of Computational Physics，2013，250：347-372.

［22］XU W Z，WU W G.An improved third-order WENO-Z scheme［J］.Journal of Scientific Computing，2018，75：1808-1841.

［23］WOODWARD P，COLELLA P.The numerical simulation of two-dimensional fluid flow with strong shocks［J］.Journal of Computational Physics，1984，54（1）：115-173.

［24］SHI J，ZHANG Y T，SHU C W.Resolution of high order WENO schemes for complicated flow structures［J］.Journal of Computational Physics，2003，186（2）：690-696.

［25］HU X Y，WANG Q，ADAMS N A.An adaptive central-upwind weighted essentially non-oscillatory scheme［J］.Journal of Computational Physics，2010，229（23）：8952-8965.