聚焦算法多樣歸類追溯算理
——三年級《兩位數乘兩位數》思考與教學

吳恢鑾

【課前思考】

研究學情，可以幫助我們深入了解學生的“前狀態”和“潛狀態”。所謂“前狀態”，主要是研究學生在學習新知識前已有的個人經驗、學習新知識的需求和學生群體之間的差異；所謂“潛狀態”，主要是研究學生在新知識學習中的可能狀態，如學生在解決兩位數乘兩位數過程中可能出現的算法的豐富性程度，它們所反映出的學生思維可能存在的層次性差異，以及可能存在的困難和障礙。

三年級學生學習兩位數乘兩位數，我們可以追問這樣兩個核心問題：兩位數乘兩位數，學生已有的邏輯基礎在哪里？學生的現實困惑在哪里？設計問卷調查時，可以把核心問題細化為兩個具體問題：學生能獨立研究出幾種兩位數乘兩位數計算方法？學生對兩位數乘兩位數豎式計算困難在哪里？

按照正常的教學進度，筆者選取了使用浙教版新思維《數學》教材的三年級70名學生進行調查。需要強調，該教材是在學生學習了乘法結合律和分配律后，再借助長方形面積模型來學習兩位數乘兩位數的，而其它同時期的教材還沒有學習乘法結合律和分配律，它們是基于乘法意義來理解兩位數乘兩位數筆算算理的。還需要補充說明的是，本次調查的樣本來自于城市學校，該校教學質量在該城區名列前茅。

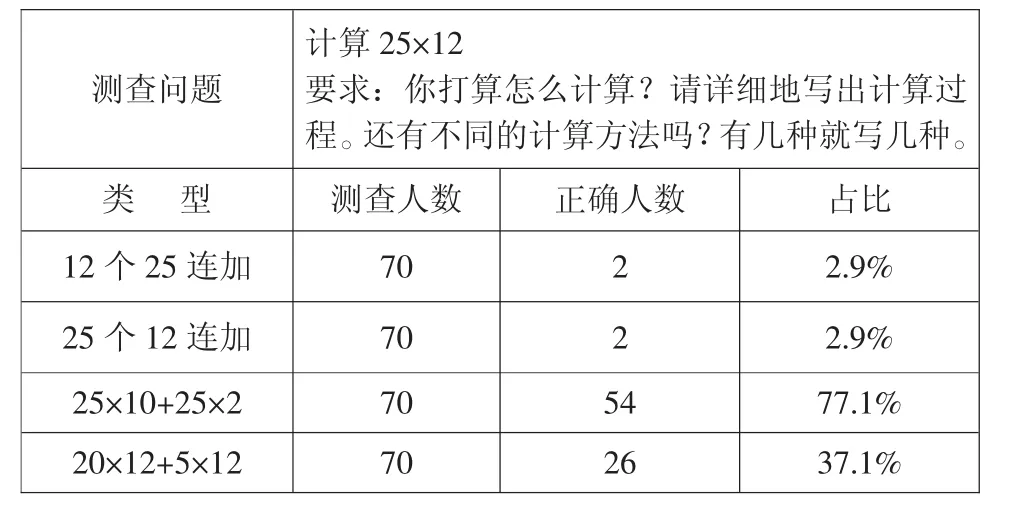
表1 學生解決兩位數乘兩位數的計算方法統計表

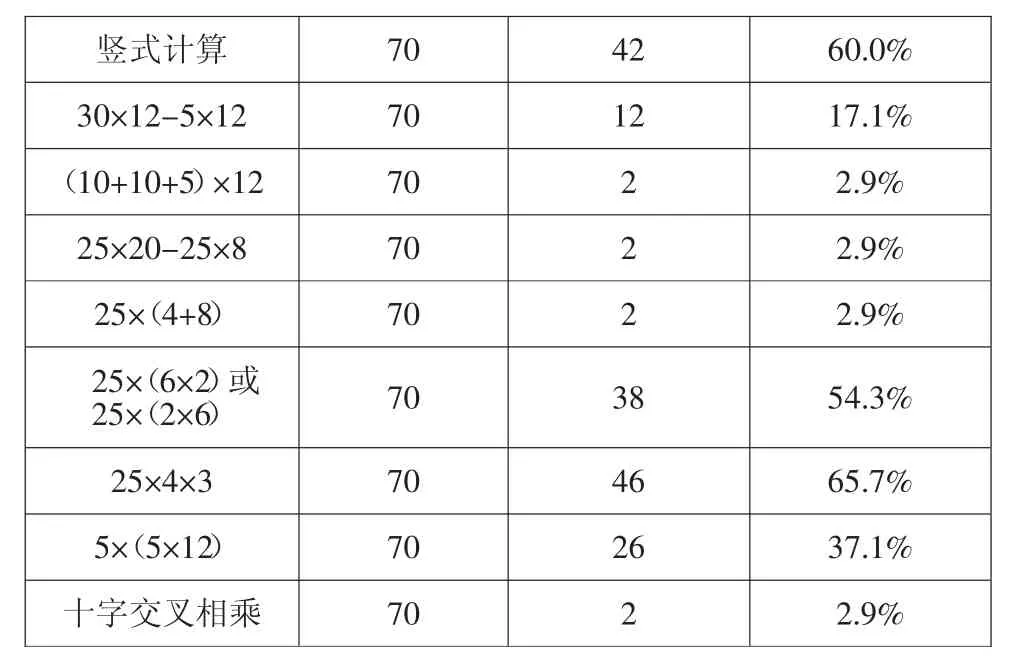
豎式計算 70 42 60.0%30×12-5×12 70 12 17.1%（10+10+5）×12 70 2 2.9%25×20-25×8 70 2 2.9%25×（4+8） 70 2 2.9%25×（6×2）或25×（2×6） 70 38 54.3%25×4×3 70 46 65.7%5×（5×12） 70 26 37.1%十字交叉相乘 70 2 2.9%

通過對上表分析可知學生已經具備了算法多樣化的基礎，教學重點在于梳理這些算法背后的算理；可以引領學生從乘法運算定律的角度對各種算法進行歸類分析，提高思維的深刻性和靈活性。

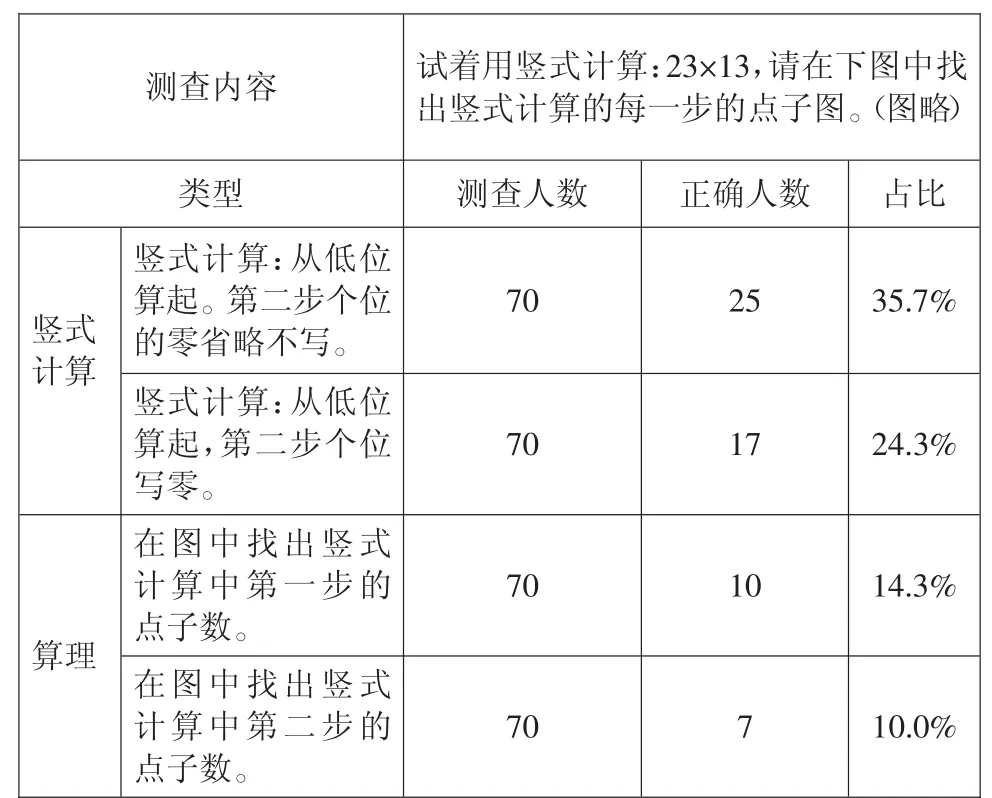
表2 學生兩位數乘兩位數豎式計算與算理理解統計表

上表給教學帶來的啟示是：要加強點子圖、橫式計算和豎式計算每步之間的溝通，從具象到抽象，再從抽象到具象，加深算法與算理之間的聯結性理解。

【教學內容】

一、研究前置，多元選擇

研究內容：25×12的計算方法。

研究要求：以下有兩張學習單，選擇一張最適合自己的學習單完成研究任務。

學習單 A：計算 25×12。

要求：你打算怎么計算，請詳細地寫出計算過程。還有不同的計算方法嗎？有幾種就寫幾種。

學習單B：學校舉行列隊表演，共有12行，每行25人，有多少人參加表演？

要求：可以先在圖上圈一圈，再寫出詳細的計算過程；也可以先寫出計算過程，再在圖上圈一圈每一步的含義。

收集全班學生的作品，并完成對學生作品質與量上的數據分析，為課中學習提供學情支撐。（具體數據見課前思考的表1、表2）

【設計意圖：研究前置，可以給學生充足的解決問題的時間和空間，同時又可以作為學情的“微調查”。待學生作品收集上來，可以全面地解讀每位學生個性化的計算方法，探尋學生的思維過程，為課中師生、生生開展深入交流奠定基礎。】

二、聚焦算法，追溯算理

1.呈現多樣算法。

任務一：你想出了幾種計算方法？分別用到了哪些知識？

任務二：哪些計算方法你沒有想到？現在你能看懂嗎？

2.全班交流算法。

第一類：拆分為兩數之積運用乘法結合律的計算方法。

生：（出示算法①）我把12拆分成4×3，然后先算出 25×4等于 100，再算 100×3等于 300。

師：把12拆分成4×3，組塊來計算，很不錯。你能從點子圖中找出25×4這部分嗎？100×3呢？（根據學生回答演示點子圖分割過程）

師：想一想，在這里用到了哪些知識？

生：在這里我用到了乘法結合律。

師：是的，在這個拆分過程中，用到了一個重要的思想方法：把兩位數乘兩位數轉化為兩位數乘一位數，也就是把新知識轉化為舊知識。大家再從剩下的七種計算方法中找一找，哪些方法也是用這種轉化思想的？

生：算法③和算法⑥。

第二類：拆分為兩數相加或相減運用乘法分配律計算的方法。

師：（出示算法⑧）同學們找出了與算法①計算方法相同的算法③和⑥，但我覺得算法⑧也很像，也出現了小括號，為什么不把它歸為一類呢？

生：這里不是把12拆成兩數相乘，而是把12拆成兩數相加的。

生：應用的是乘法分配律不是乘法結合律。

師：真有一雙會分析的數學眼光。你能從這點子圖中找出各部分的含義嗎？

生：（學生上臺指著點子圖）25乘10就是先算出每行25人，10行是250人；25乘2就是每行25人，2行是50人。

師：在這里把12拆成了兩數相加，然后運用乘法分配律，把兩位數乘兩位數轉化為兩位數乘整十數和兩位數乘一位數。你們為什么不把12拆分成9加3，而是10加2呢？

生：10加2計算時更加簡便一些。

師：在轉化新知的時候，還要考慮它的簡便性。

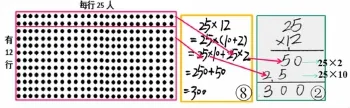
師：（出示算法②）有些同學是用豎式計算的，你覺得它和橫式有共同的地方嗎？誰愿意來先介紹一下豎式是怎么計算的？

生：堅式也是先算2乘25，得到50，再算10乘25，得到250，第二步只要把5寫在十位上就可以了，個位0可以不用寫，然后再把兩部分加起來。

生：我有一點補充，第二步的“25”的5一定要寫在十位上。

師：補充的很好，請大家一起思考：（1）豎式第一步中的“50”，代表點子圖多少行的人數？（2）豎式第二部中的“25”，代表點子圖多少行的人數？（3）這里的“50”和“25”誰大誰小？為什么？（學生回答略）

師：觀察點子圖、橫式和豎式計算，它們之間有什么聯系？

生：豎式中的50，在橫式中就是25×2，在圖中就是表示2行的人數，豎式中的“25”，在橫式中就是25×10，在圖中就是表示整10行的人數。

師：兩位數乘兩位數橫式計算和豎式計算有什么相同的地方？

生：它們都是把12拆成10加2，都用到了乘法分配律。方法一樣，只是形式不一樣。

師：找一找，和算法②、⑧計算方法類似的還有哪些？

生：算法④和算法⑤。

生：我覺得算法⑦也一樣的。這里也用到了乘法分配律。

師：我們回到點子圖去找一找各部分的含義，再判斷是不是用到了乘法分配律。誰能結合點子圖來說一說？

生：我是這樣想的，先假設每行是30人，那就是30乘12，因為每行多算了5人，所以要減去5乘12。（教師根據學生的敘述動態演示過程）

第二，通過雙學位聯合培養項目可以豐富學生的人生閱歷，開拓學術視野，優化知識結構，提高實踐能力，同時加深校際的交流與合作。

3.比較異同。

出示：第一類：①、③、⑥

第二類：②、④、⑤、⑦、⑧

師：我們把這八種計算方法，分成了兩類，大家觀察一下，每一類的計算方法有什么共同的地方？第一類和第二類有什么不同的地方？第二類五種方法又有什么不同的地方？

師：這八種方法，你喜歡哪一種？為什么？

生：我喜歡豎式計算，感覺它是萬能的。

生：我覺得如果能轉化25×4這樣的整百數，其實也是簡便的。

生：哪種方法好，還要看數據特點。

4.更一般的計算。

（出示：23×19）

師：剛才哪些方法還適合計算23×19？請你選擇合適的方法試一試。

生：這兩個數都不能拆成兩個數相乘了，所以我把19拆成了10+9再來計算。

生：第一類的方法都不合適了，可以用第二類的方法來計算。

生：用豎式方法肯定可以。

師：請大家用豎式計算23×19。

（分析錯例，鞏固豎式計算，進一步內化算理）

【設計意圖：展示八種典型的計算方法，然后選取最具代表性的兩種計算方法①和⑧，借助點子圖，讓學生自主分析每種算法的依據與策略，從拆分方法、運算律、轉化思想三個角度，進行了追溯分析，抓住了數學本質。然后安排學生尋覓與①和⑧相同的方法，引領學生對八種典型算法進行歸類討論，使學生認識到兩位數乘兩位數眾多的算法，其實就是兩類：一類拆成兩數相乘，用乘法結合律完成運算；一類拆成兩數相加或兩數相減，用乘法分配律完成運算，而豎式計算與橫式計算道理都是一樣的，只是形式上不同而已。最后通過算式23×19，聚焦豎式。至此，學生完成以兩位數乘法計算為載體，經歷了算法的分析、辨別和算理的反思、應用的過程，發展了運算能力。】

三、應用練習

師：我們班一位同學用這樣連線的方法計算出了25×12的結果。請問，你到底是怎么計算得到的呢？請向大家更加詳細的介紹一下。

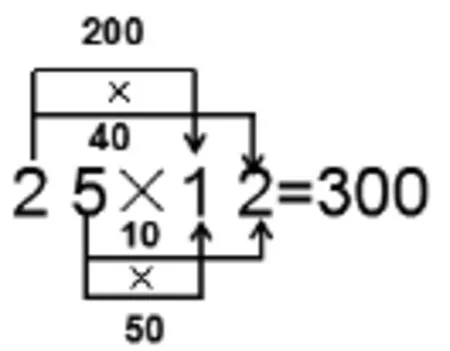
生：我是想用25的5和12的10相乘得50，然后5和2相乘得10；再用25的20和12的10相乘得200，然后20和2相乘得40，再加起來就是300。

師：我們借助點子圖來演示一下他剛才介紹的計算方法。

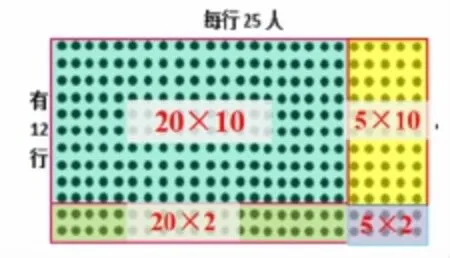
師：我們也可以借助表格來理解他的計算方法。

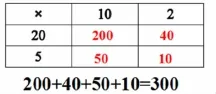
師：其實這位同學在計算中也是應用到了乘法分配律，這樣的乘法分配律在初中整式乘法中會經常用到，有興趣的同學課后可以再研究，當然也鼓勵大家課后去收集更多更有趣的兩位數乘兩位數的計算方法。

【設計意圖：展示一位學生的“十字交叉相乘法”，目的不在于讓每位學生都掌握，而是為了拓開學生的思維視野，引發學生探究興趣，也為今后乘法分配律在整式乘法中的應用積累一點基本經驗。】