應用GPS技術建立獨立坐標系的探討
張 宇
GPS技術在測繪工程領域有著廣泛的應用,目前在工程測量中采用GPS技術建立工程控制網已成為最主要的手段之一。工程控制網是直接服務于大比例尺測圖和施工測量的,其所提供的距離應盡可能的與實測距離保證一致。我國《工程測量規范》中,要求長度綜合變形不超過2.5 cm/km,這樣可以使國家統一坐標成果直接運用于工程建設中。但實際測量工作中,經常遇到測區長度綜合變形超過2.5 cm/km,在這些地區進行工程測量時,直接采用國家統一坐標系統成果,控制點間邊長往往與實測距離有較大差值,使國家統一坐標系統成果不能直接運用于工程建設。這種情況下,建立適合工程范圍的獨立坐標系使長度綜合變形在允許范圍內,保證控制點間邊長與實測距離盡可能的一致,使平面坐標成果可以直接服務于工程建設中,就顯得十分有必要了。
1 長度變形分析
地面觀測長度歸算到參考橢球面上產生的變形和參考橢球面上的邊長歸算到高斯投影面產生的變形,是長度變形產生的原因。
把高斯投影平面上的長度與地面觀測長度的差值,稱為長度綜合變形:

式(1)中,δ為長度綜合變形,ym為端點間平均橫坐標,R為測區中心的平均曲率半徑,Hm為長度所在高程面對于橢球面的高差,RA為邊長所在方向的橢球曲率半徑,s為地面觀測長度。
取 R≈RA≈6371 km,S≈s,則式(1)可寫成下式:

式中,y表示測區中心的橫坐標,H表示測區平均高程,y與H均以km為單位。
式(2)可以看出,長度綜合變形與測區中心橫坐標和測區平均高程有關。
2 獨立坐標系的建立方法
通常建立獨立坐標系有三種方法,分別為:選擇“抵償高程面”作為投影面;選擇“任意投影帶”;選擇通過測區中心的子午線作為新建獨立坐標系的中央子午線,平均高程面作為投影面。
2.1 選擇“抵償高程面”作為投影面
由公式(1)可以看出,將地面觀測值歸算至參考橢球面,長度是變小的;將參考橢球面上觀測值歸算至高斯投影面上時,長度是變大的。兩個歸算過程能夠相互抵消,若選擇一個最恰當的參考橢球參數,使得地面觀測值歸算至參考橢球面的減小的值與參考橢球面上觀測值歸算至高斯投影面上增加的值相等,那么長度綜合變形就能完全抵消。這個最恰當參考橢球面,就是抵償高程面。
為了完全抵消長度綜合變形,令δ=0,由式(1)可以得到:

取 R≈RA≈6371 km,S≈s,則:

利用式(4)可以計算出抵償高程面,確定新的參考橢球參數。
2.2 選擇“任意投影帶”
通過將中央子午線移動恰當位置,使得測區在新投影帶內,地面觀測值歸算至參考橢球面的變形與參考橢球面上觀測值歸算至高斯投影面上的變形相等,從而消除長度綜合變形在控制測量中的影響,使得高斯投影平面上控制點間邊長與實測值保持一致。
這種通過移動中央子午線重新建立坐標系,抵償長度綜合變形的投影帶就是任意投影帶。運用這種方法建立坐標系時,它的參考橢球與原參考橢球是相同的。
令 δ=0,由式(1),可以得到

式(5)可以看出,將中央子午線西移至距測區中心為ym的位置,可以消除測區中心的長度綜合變形。
2.3 選擇平均高程面作為投影面,通過測區中心的子午線作為中央子午線
這是前兩種方法的一種結合體,就是既移動中央子午線,又選擇投影面。與前兩者的區別在于,它將新建立坐標系的中央子午線選在了測區中心,將投影面選在了測區平均高程面。有時候也可以將測區平均高程面再下移一點作為投影面。
這種坐標系的建立方法因其簡單有效的特點,在工程測量中應用廣泛。其實質是保證測區中心y≈0處,H≈0,從而使δ=0。
令 ym=0,由式(1)可以得到:

因δ/S≤1/40000,則Hm最大為159 m,即平均高程面最大下移高度。
同理,因 δ/S≤1/40000,取 R=RA=6371 km,由式(1)得到

可以看出,選擇平均高程面作為投影面,通過測區中心的子午線作為中央子午線,建立的平面坐標系能夠滿足長度綜合變形的范圍為:2ym最大≈127 km。
由文獻[1]知道,第三種方法抵償范圍最大。
2.4 新橢球參數的求取及坐標轉換
采用第1種和第3種建立獨立坐標系的方法,都改變了參考橢球投影面高程,因此必須要重新計算新橢球參數。
計算新橢球參數時,新橢球與原橢球相似,長半徑a和短半徑b變化,但扁率f及偏心率e不變。原橢球面上控制點的大地坐標轉換到新的橢球面上,大地經度不變,但大地緯度改變[2]。
設測區平均緯度為Bm,對應的橢球測區平均半徑為Rm,新選橢球面至原橢球面高程為H,對應新選橢球測區平均半徑為Rx,新選橢球長、短半徑分別為ax、bx。參考文獻[2]有以下公式:


設控制點的大地坐標在原橢球上為(B,L),在新選橢球上為(Bx,Lx), 參考文獻[2]有下列公式:

式中,M為子午圈曲率半徑;N為卯酉圈曲率半徑,;W為第一基本緯度函數
3 工程實例數據分析
3.1 測區概況
渭河下游部分河段概略位置為東經 108°40′~110°18′,北緯34°19′~34°40′,東西長度約 208 km,海拔高程約 300~360 m。采用GPS技術建立該區域的平面控制網,坐標系統為2000國家大地坐標系。
3.2 長度變形分析
測區橫跨3°投影帶的36、37帶,在第36、37帶的邊緣處,長度綜合變形最大。以36、37帶的交界處經度109°30′、緯度34°30′、測區平均大地高330 m,計算測區中心的長度變形情況。由式(1)得,

可見,在測區中心(即3°投影帶的第36、37帶交界處)投影變形較大,無法滿足長度綜合變形的容許范圍,故不能直接采用國家3°帶統一坐標。由于測區較長,需要采用分區投影的方法建立獨立坐標系統。
3.3 獨立坐標系建立方法
測區基本在3°帶第36、37帶之間,且測區兩端距離第36帶中央子午線108°子午線、第37帶中央子午線111°子午線基本一致,將測區平均分為兩個分區。本文只說明36帶范圍內獨立坐標系的建立方法。
首先確定36帶范圍內測區中心位置為經度109°05′,緯度34°26′,測區平均大地高為 340 m。
由式(9),測區平均曲率半徑Rm=6370387.464 m。
由式(1),得:
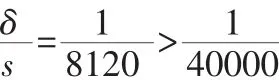
可以看出測區中心投影變形仍然較大,無法滿足長度綜合變形的容許范圍,不能直接采用國家統一坐標。
由上可知,采用選擇平均高程面作為投影面,通過測區中心的子午線作為中央子午線建立獨立坐標系時,平均高程面最大下移高度159 m時,獨立坐標系滿足投影變形的范圍最大,滿足中央子午線左右范圍內63.5 km的區域,合計范圍為127 km。故將投影面選為340 m-159 m=181 m。
綜上,以測區中心經度109°05′為中央子午線,投影高程面為181 m建立獨立坐標系。
3.4 新橢球的參數的計算
通過式(8)-(12)計算新橢球的參數:

3.5 將國家控制點從國家統一坐標成果轉換至獨立坐標系統成果
表1為測區附近的國家控制點平面坐標。國家控制點名稱及坐標均經過相關保密處理。

表1 國家等級控制點成果
通過高斯反算計算出原橢球下的大地坐標,再通過式(13)~(15)計算出國家控制點大地緯度的變化量及其新的大地緯度,最后計算出以上國家控制點在新建獨立坐標系下的平面直角坐標。表2為國家控制點在獨立坐標系中的平面坐標。
以國家控制點在獨立坐標系下的平面直角坐標為起算點,對外業觀測數據進行平差,得到獨立坐標系的平面坐標。表3為部分控制點平面坐標。

表2 國家控制點在獨立坐標系中的平面坐標(中央子午線為109°05′,投影高程面為181 m)

表3 部分控制點平面坐標(中央子午線為109°05′,投影高程面為181m)
為檢驗獨立坐標系是否滿足長度綜合變形容許數值要求,采用拓普康3002LNC全站儀(標稱精度±2 mm+2 ppm×D)對表3中控制點進行了邊長檢測,檢測結果見表4。

表4 實測邊長與平差結果對比情況
可以看出測區內控制點間實測邊長與平差成果邊長差值滿足長度綜合變形容許數值1/40000要求,建立的獨立坐標系能夠滿足實際工程建設需要。
4 結語
(1)建立工程控制網時,首先通過長度變形分析來確定是否需要建立獨立坐標系。若需要建立獨立坐標系時,要根據測區的實際情況來選擇最簡單、有效的減少長度綜合變形的方法來建立獨立坐標系。
(2)當改變參考橢球投影面高程時,必須要重新確定新橢球參數,這也是建立獨立坐標系的重點。
[1]馮林剛.GPS測量控制網納入獨立坐標系的方法[J].地礦測繪,2000(3):6-8.
[2]董鴻聞,李國智,陳士銀,等.地理空間定位基準及其應用[M].北京:測繪出版社,2004.
[3]銀志敏,王軍,馬全明,等.城市軌道交通工程平面控制測量坐標系統投影面轉換方法的應用研究[J].測繪通報,2015(5):109-112.
[4]張鳳舉,張華海,趙長勝,孟魯閩,盧秀山編著.控制測量學[M].北京:煤炭工業出版社,1999.
[5]楊國清主編.控制測量學(第2版)[M].鄭州:黃河水利出版社,2010.
[6]孔祥元,郭際明主編.控制測量學(第三版)[M].武漢:武漢大學出版社,2007.

