基于四元數法的航向修正算法分析

戚憲東,郭英,孫玉曦,姬現磊

(山東科技大學 測繪科學與 工程學院,山東 青島 266590)

0 引 言

捷聯慣導將陀螺儀和加速度計直接安裝在載體上,省掉了機電式導航平臺,利用計算機軟件建立一個“數學平臺”來代替機電平臺實體。由于其結構簡單且抗干擾能力強,目前已成為導航定位、無人機、智能交通等領域的研究熱點之一[1]。

姿態解算是捷聯式慣性導航系統的關鍵技術,通過姿態矩陣可以得到載體的姿態和導航參數計算需要的數據,是捷聯式慣導算法中的重要工作[1]。載體的姿態和航向體現了載體坐標系與導航坐標系之間的方位關系。用于描述載體坐標系與導航坐標系轉換關系的方法主要有歐拉角法、方向余弦法和四元數法等[2]。其中,歐拉角法在求解姿態時存在奇點,不能用于全姿態的解算[3];方向余弦法可用于全姿態的解算但計算量大,不能滿足實時性要求[4];四元數法算法簡單,易于操作,只需要求解四個參數,計算量小,可以在實現過程中修正漂移,應用比較廣泛[5]。而四元數微分方程的解算主要用到龍格-庫塔法[6],文獻[7]介紹了一階龍格-庫塔法,其存在解算精度和效率較低的問題;文獻[8]詳細敘述了四階龍格-庫塔法,在解算時收斂性較好,穩定性較高。因此,尋求一種收斂性好和穩定性高的高階計算方法,能夠高效、快速的解算四元數微分方程,保證四元數解算航向的精度。

在姿態解算過程中,除了優化解算方法外,還存在陀螺儀長時間工作的漂移誤差。消除由陀螺儀的漂移誤差導致的航向誤差一直是阻礙室內定位精度提升的難點[9],為了減少航向誤差,研究人員提出了幾種航向修正的方法:Borenstein等人[10]提出了基于腳踏式慣性測試單元(IMU)的啟發式偏移減少算法(HDR)和啟發式漂移消除算法(HDE)。樓喜中等人[11]在HDE的基礎上,將航向角作為直接修改的對象,消除了部分陀螺儀積分誤差。

本文利用行人在室內直線運動情況下的航向角偏差作為誤差反饋回系統,來修正陀螺儀的角速度輸出,從而抑制陀螺儀的漂移,進而修正四元數法解算的航向,并將其與參考航向對比以驗證四元數法的正確性和有效性,并分析不同采樣頻率下的二階龍格-庫塔法與四階龍格-庫塔法解算航向精度,得到提高采樣頻率能減少航向解算誤差,提高定位精度,對捷聯式慣性導航技術有一定的應用參考價值。

1 系統模型

1.1 姿態矩陣的描述

通常假定捷聯系統“數學平臺”模擬地理坐標系,即導航坐標系;而確定載體的姿態矩陣即為研究載體坐標系(b系)和導航坐標系(n系)的空間轉動關系,一般用載體坐標系相對導航坐標系的三次轉動角確定[1]。載體的姿態由橫滾角γ,俯仰角θ,航向角φ來描述。

1.2 四元數微分方程

隨著捷聯式慣性導航技術的發展,為了更簡便地描述剛體的角運動,采用了四元數這個數學工具,用它來彌補通常描述剛體角運動的3個歐拉角參數在設計控制系統時的不足[3]。

規定q為一個四元數向量,即:

(1)

則q滿足微分方程:

(2)

四元數姿態矩陣的微分方程只要解四個一階微分方程式即可,計算量小,容易實現,是導航解算中常用的方法。

2 基于四元數的航向解算

常用的姿態描述方法有:歐拉角法、方向余弦法和四元數法。由于相對比其他兩個方法,四元數方法具有計算簡單、易于操作、且能避免出現歐拉角所產生的“奇點”問題的優點,故本文選擇四元數法來解算姿態信息。

2.1 四元數法姿態矩陣計算的步驟如下:

第1步:初始化四元數。初始姿態信息設置:航向角為90°、俯仰角和橫滾角都設置為0°.初始化四元數(q0,q1,q2,q3)為

(3)

式中:φ0、θ0、γ0分別為初始的航向角、俯仰角和橫滾角。

第2步:四元數微分方程的實時解算。下面簡述二階龍格-庫塔法和四階龍格-庫塔法解算四元數微分方程的基本原理:

方法1:利用二階龍格-庫塔法實時更新四元數。

解算公式[6]:

(4)

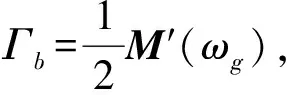
(5)

根據上述公式即可獲得用二階龍格-庫塔法實時更新的四元數。

方法2:利用四階龍格-庫塔法實時更新四元數。

解算公式[8]:

(6)

式中:T為步長;q(t)、q(t+T)分別為t、t+T時刻的四元數。根據上述公式即可獲得用四階龍格-庫塔法實時更新的四元數。

第3步:四元數歸一化

(7)

第4步:由四元數計算旋轉矩陣并計算航向角φ

(8)

(9)

通過以上步驟的解算,可以利用陀螺儀輸出的角速度數據得到行人航向,但由于陀螺儀的輸出會隨著時間的增長而產生漂移,從而影響航向解算精度。

2.2 航向修正的改進HDE算法

基于室內環境下,行人多為直線行走的情況,其航向角變化較小,利用航向角偏差作為誤差反饋回系統,來修正陀螺儀的角速度輸出,從而抑制陀螺儀的漂移,提高定位精度,具體算法步驟如下。

第1步:判別行人運動狀態

通常利用當前航向與歷史航向的變化幅值來判斷行人的運動軌跡是否為直線:

(10)

如果Δφi<10°時,則表示航向變化不明顯,判定行人沿著直線行走。

確定行人沿直線行走后,采用下式對航向進行修正:

(11)

第2步:設置主導航向

行人初始的主方向為0°,沿著順時針方向依次為45°、90°、135°、180°、225°、270°、315°,一共8個主方向,角度間隔δ為45°,當前航向與主航向的偏差可用下式計算:

(12)

式中:INT(x)為取整函數;φi為當前航向角。

利用改進的HDE航向修正算法,對行人在室內環境下的直線行走情況進行修正,抑制了陀螺儀的漂移,提高了定位精度。

2.3 行人運動軌跡推算

將經HDE算法修正過的航向角信息與加速度計分析所得的步長信息相結合,獲得精確的定位信息。基于慣性傳感器的行人室內定位的關鍵技術是行人航跡推算(PDR)。所謂航跡推算,即由上一位置的坐標結合當前一步的航向角信息與步長信息求解當前位置的坐標,公式為[11]

(13)

式中:x,y為位置坐標; S為步長。

3 實驗結果與分析

3.1 數據采集

實驗采用低成本的魅藍NOTE3手機作為行人導航數據采集模塊,進行測試實驗。本文利用安卓軟件“導航項目(AndroSensor)”為工具來獲取傳感器數據,該軟件簡單實用,可以滿足實驗的需求。為了達到較高的測量精度,在采集數據之前要對手機的內置傳感器進行校準,加速度計和陀螺儀要進行零偏校準。

實驗數據采集頻率分別設為100 Hz、200 Hz,實驗人員手持智能手機,平放于身前,以正常步速按設計的路線行走。行走路線以主導方向行走為主,實驗場地為山東科技大學測繪學院辦公樓的回型走廊,行走的矩形路線長為62 m、寬為42 m.

3.2 實驗分析

不同采樣頻率下,利用二階龍格-庫塔法和四階龍格庫塔法解算四元數微分方程,對解算的行人航向進行HDE算法修正后,推算行人航跡如圖1所示。

分析實驗結果如表1所示。

表1 實驗精度分析

注:TTD為路線閉合差與其總路線的比值

由圖1和表1分析可知:

1) 本算法的解算結果與參考路徑對比,驗證了四元數法解算航向的有效性和可行性。

2) 二階龍格-庫塔法與四階龍格-庫塔法解算四元數微分方程,用四元數表示歐拉角,并用HDE算法修正航向,推算行人軌跡,其在100 Hz采樣頻率下,軌跡閉合差分別為2.847 m和2.813 m;200 Hz采樣頻率下,軌跡閉合差分別為1.164 m和1.159 m,解算結果相差不大,主要是由于兩種方法解算的是更新后的四元數,其在轉換為歐拉角以及HDE算法修正航向的過程中,原始數據進行了處理,導致高階方法解算結果優勢并不是很明顯。

3) 當提高采樣頻率至200 Hz后,行人軌跡與參考路線較為吻合,且二階龍格-庫塔法解算行人軌跡閉合差減小了1.683 m,TTD誤差大大減小;四階龍格-庫塔法解算行人軌跡閉合差減小了1.654 m,TTD誤差也大幅減小。驗證了在傳感器一定工作范圍內,提高采樣頻率,可以減小航向解算誤差,提高定位精度。

4 結束語

本文以低成本智能手機為實驗對象,選用四元數法解算載體航向信息、二階龍格-庫塔法和四階龍格-庫塔法分別進行四元數更新,然后把經過四元數解算的航向信息通過改進的HDE算法修正后,與步長信息相結合,實現位置解算。實驗分析了不同采樣頻率下的二階龍格-庫塔法與四階龍格-庫塔法解算的航向精度,結果表明，提高采樣頻率能減少航向解算誤差,提高定位精度。本文工作對實際導航定位工作具有一定的指導意義。

[1] 張榮輝,賈宏光,陳濤,等. 基于四元數法的捷聯式慣性導航系統的姿態解算[J]. 光學精密工程, 2008, 16(10):1963-1970.

[2] 王立波. 捷聯慣導系統設計與數據處理技術研究[D]. 西安:西安電子科技大學, 2011.

[3] 黃國英. 微分方程初值問題的加權改進歐拉數值解法[J]. 成功:教育版, 2011(8):287-287.

[4] 李連仲,王小虎,蔡述江. 捷聯慣性導航、制導系統中方向余弦矩陣的遞推算法[J]. 宇航學報, 2006, 27(3):349-353.

[5] 王彤,馬建倉,秦濤,等. 基于旋轉四元數的姿態解算算法[J]. 彈箭與制導學報, 2014,34(3):15-16.

[6] 楊陽. 龍格庫塔法求模糊微分方程的數值解[D]. 哈爾濱:哈爾濱工業大學, 2015.

[7] 張麗娟,張翔,關天冶. 一階常微分方程初值問題的數值算法[J]. 通化師范學院學報, 2017, 38(8):22-24.

[8] 馮建強,孫詩一. 四階龍格——庫塔法的原理及其應用[J]. 數學學習與研究, 2017(17):3-5.

[9] 曾慶軍,劉慧婷,張明. 基于HDR的陀螺儀隨機漂移分析與處理[J]. 江蘇大學學報(自然科學版), 2016, 37(3): 332-336.

[10] BORENSTEIN J, OJEDA L. Heuristic drift elimination for personnel tracking systems[J]. Journal of Navigation, 2010, 63(4): 591-606.

[11] 樓喜中,周樂宇,葉敏展, 等. 基于角度的HDE算法在室內行人航跡定位中的研究[J]. 傳感技術學報, 2015,28(4): 598-602.