從數形結合角度解絕對值不等式

吳遠覺

絕對值不等式的常見解法有定義法、平方法、零點分區法，要點在于去掉絕對值。如果運用絕對值的幾何意義，或者運用絕對值函數圖像，從數形結合角度來解絕對值不等式，則顯得直觀、簡便。下面筆者結合實例加以說明。

例1（2017年全國卷Ⅲ）已知函數f（x）=|x+1|-|x-2|，求不等式f（x）≥1的解集。

解析：|x+1|-|x-2|表示x與-1的距離和x與2的距離之差，f（x）≥1表示這個差不小于1。結合數軸可知，x需位于1或者1的右邊（如圖1），故不等式的解集為{x|x≥1}。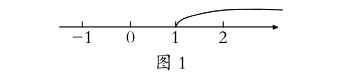

當然也可以通過零點分區討論求解，還可以作出函數f（x）與y=1的圖像，從圖像上發現f（x）的解是{x|x逸1}。

例2（2009年遼寧卷）設函數f（x）=|x-1|+|x-a|。

（1）若a=-1，解不等式f（x）≥3；

（2）如果x∈，f（x）≥2恒成立，求a的取值范圍。

解析：（1）a=-1時，f（x）=|x-1|+|x+1|表示x到-1的距離和到1的距離之和。如圖2，當x位于-1和1中間時，f（x）=2<3，顯然不成立，故x需位于-1左側或者1的右側。由線段長可知，x∈（-∞，-1.5]∪[1.5，+∞）。

（2）x∈，f（x）≥2恒成立表示f（x）的最小值大于等于2。而f（x）最小時x位于1和a的中間，故a應該在1的左邊或者右邊最少相距2的位置，故a∈（-∞，-1]∪[3，+∞）。

本題常規做法需要對a與1進行比較，分三種情況討論，顯得繁瑣。數形結合讓題目變得簡單直觀，方便快捷。

華羅庚先生說：“數缺形時少直觀，形缺數時難入微。”數形結合作為中學階段一種非常重要的數學思想方法，需要平時多滲透、訓練，才能切實提高學生的解題能力。

（作者單位：長沙麓山外國語實驗中學）