基于擴散動力模型的鋰離子蓄電池放電速率與放電容量相關性研究

雷 雨，李 銳，余佳玲

（陸軍工程大學通信士官學校，重慶400035）

自從20世紀90年代鋰離子電池出現以來，因其高比能量、高比功率、高效率、長循環壽命、低自放電率等優點而得到了廣泛應用。但由于諸多因素影響，如使用溫度、充放電速率、制造工藝等，對其狀態的精確評估一直是難點。電池容量是評價蓄電池性能優劣的重要指標之一。本文著眼于研究在恒流放電條件下，鋰離子電池的放電速率與放電容量之間復雜的非線性關系，以鋰離子電池擴散動力模型為基礎，建立電流放電速率與容量之間的對應關系，同時與現在被廣泛采納的Peukert經驗公式進行對比實驗驗證，證明其有效性。

1 Peukert方程恒流放電容量預測模型

電池的兩個最重要的特性是電壓和容量；這兩個量的乘積是儲存在電池里的能量的量度。對于理想電池來說，電壓保持恒定，直到它完全放電為止，然后電壓降到零。在理想情況下，電池在每一個負載條件（即不同的放電電流）下，放電容量是相同的。現實情況并不是這樣，在放電時，電壓會下降，在較高負荷（高放電電流）條件下，有效容量會降低。這種現象被稱為速率容量效應。

在理想情況下，很容易計算電池的使用時間。在恒定負載（恒流放電）情況下，放電持續時間L是容量(C)除以負載電流(I)：

由于各種非線性效應，這種關系不適用于實際電池。

1898年，Peukert在鉛酸蓄電池恒流放電試驗中發現恒流放電電流與持續放電時間／容量關系的經驗公式，稱作Peukert方程，其規律稱作Peukert定律。恒定負載（恒流放電）條件下，放電時間可以用Peukert定律進行簡單估計：

這里a ＞ 0,b ＞ 1，它們是常量，取決于電池本身。

2 擴散模型研究

2.1 菲克定律

菲克定律[1]包括兩個內容：

1）根據菲克第一定律，在單位時間內通過垂直于擴散方向的單位截面積的擴散物質流量（稱為擴散通量Diffusion flux,用J表示）與該截面處的濃度梯度成正比（比例系數為D）。

2）菲克第二定律是在第一定律的基礎上推導而來的。菲克第二定律指出，在非穩態擴散過程中，在距離一端x處，濃度隨時間的變化率等于該處擴散通量隨距離變化率的負值。

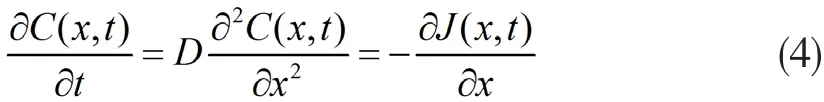
簡單概括，就是某液面與相鄰液面之間的流量正比于兩者之間的濃度差，而該液面濃度隨時間的變化率等于其分別與相鄰兩液面之間的流量差（流入流量－流出流量）。

2.2 擴散模型

假設電池內兩個電極的反應過程是對稱的，可以只考慮一個電極。

將電池電極內的電解液平均劃分，離散化為m等份（圖1），將第n等份（距離電極最近的為第1等份）的電荷量設為,設電極電解液寬度為w,根據菲克第一定律，可以得到每一時刻該部份流入、流出的流量：

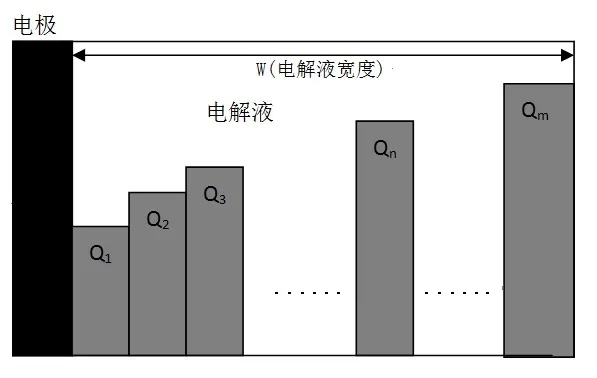
圖1 擴散模型

引入高度的定義，即令每一部分的高度等于電量除以該部分的標準化寬度（該部分寬度除以電極電解液的寬度w，即寬度/w），可以得到：

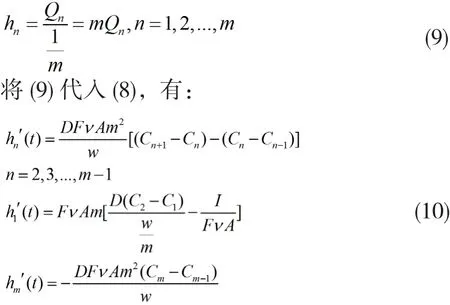
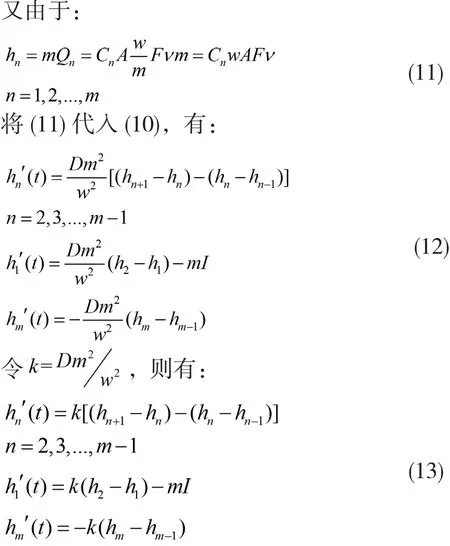
3 Kinetic Battery Model恒流放電模型

Kinetic Battery Model[2]由曼維爾和麥克格文在1993 年提出。最初，該模型是針對鉛酸蓄電池的，但是分析顯示，它也適用于其他種類電池的放電模型。

3.1 Kinetic Battery Model理論

在模型中，電池電量分為兩個部分：有效電荷部分(available-charge well)和束縛電荷部分(bound-charge well)，如圖2所示。

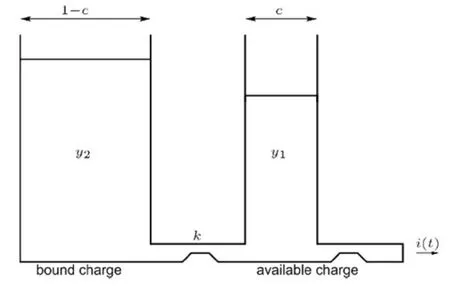
圖2 動力模型（Kinetic Battery Model）

引入比重系數c(0 ＜ c ＜ 1)來表示有效電荷部分（表示為表示束縛電荷部分（表示有效電荷部分可以直接提供負載使用而束縛電荷部分僅向有效電荷部分提供電荷。電荷由束縛部分向有效部分的流動通過一個固定的“閥門”，的量綱是1/時間，并制約了兩部分電荷（束縛電荷、有效電荷）之間流動的速率。在這個參數外，兩個部分之間的流動速率依賴于兩者之間的高度差。與電解液擴散過程研究中關于高度的定義（參見式(9)）相類似，定義兩個部分的高度如下：

初始條件：為電池的容量。如果電池的有效電荷部分無電荷剩余，即可以認為電池已經耗盡。

電池的放電過程可用圖3所示。

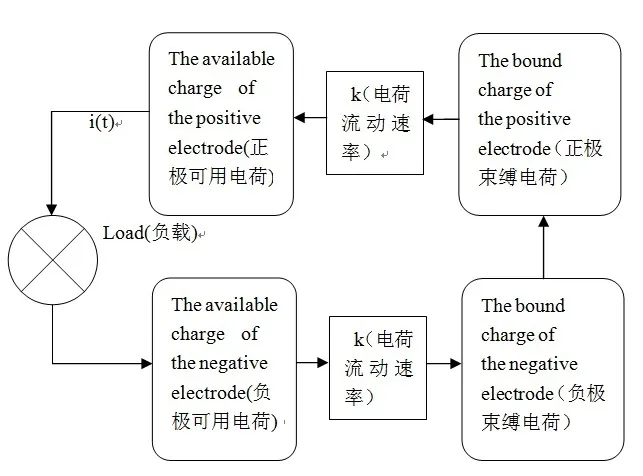
圖3 蓄電池放電過程示意圖

對比(13)-(17)，當m=2時，(13)即為Kinetic Battery Model（動力模型）取c=0.5的情形。當電解液不等分為兩部分時（m=2,n=1為有效電荷，寬度為c；n=2為束縛電荷，寬度為1-c）時，可由擴散模型的推導過程推出Kinetic Battery Model的系統微分方程(16)(17)。可見，Kinetic Battery Model是擴散模型的離散化近似。以上推導過程，從電池的電解液遵循菲克定律擴散的角度，為Kinetic Battery Model提供了依據。Kinetic Battery Model并不僅是數學公式的近似，而是具有物理含義。實際上，當時式(13)就是由Rakhmatov和Vrudhula于2001年提出的模型（Rakhmatov and Vrudhula’s diffusion model）[3]。

3.2 Kinetic Battery Model恒流放電模型

當考慮恒流放電時，,微分方程組很容易求解，根據電池耗盡的條件（有效電荷部分無電荷剩余），可以求出放電時間L。

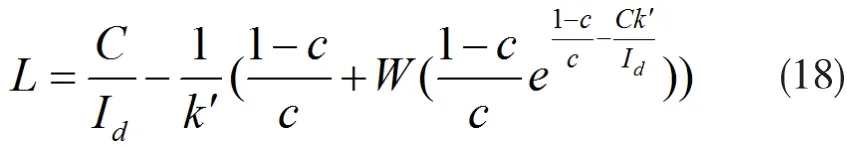
其中W(.)是蘭伯特W函數，蘭伯特W函數是的反函數。

由于是恒流放電，由(18)，可以得到放電容量

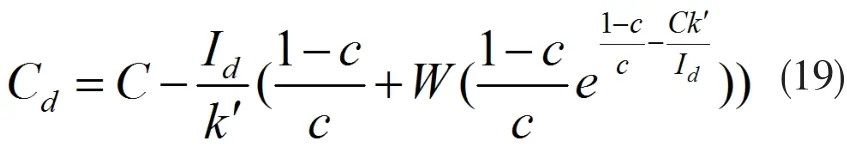
4 模型驗證與對比

實驗：額定容量為1500mAh的磷酸鐵鋰電池每經過一定次數（50至60次）的充放電循環（工步：300mA恒流充電至3.65V——3.65V恒壓充電至電流小于10mA——靜置1h——300mA恒流放電至2.5V）后，將電池充滿靜置（300mA恒流充電至3.65V——3.65V恒壓充電至電流小于10mA——靜置1h）,對實驗電池進行不同電流條件下（600mA、1000mA、1500mA、2000mA）的恒流放電實驗（放電終止電壓均為2.5V），然后繼續進行充放電循環，直到電池的容量小于額定容量的80%，認為電池壽命終止。

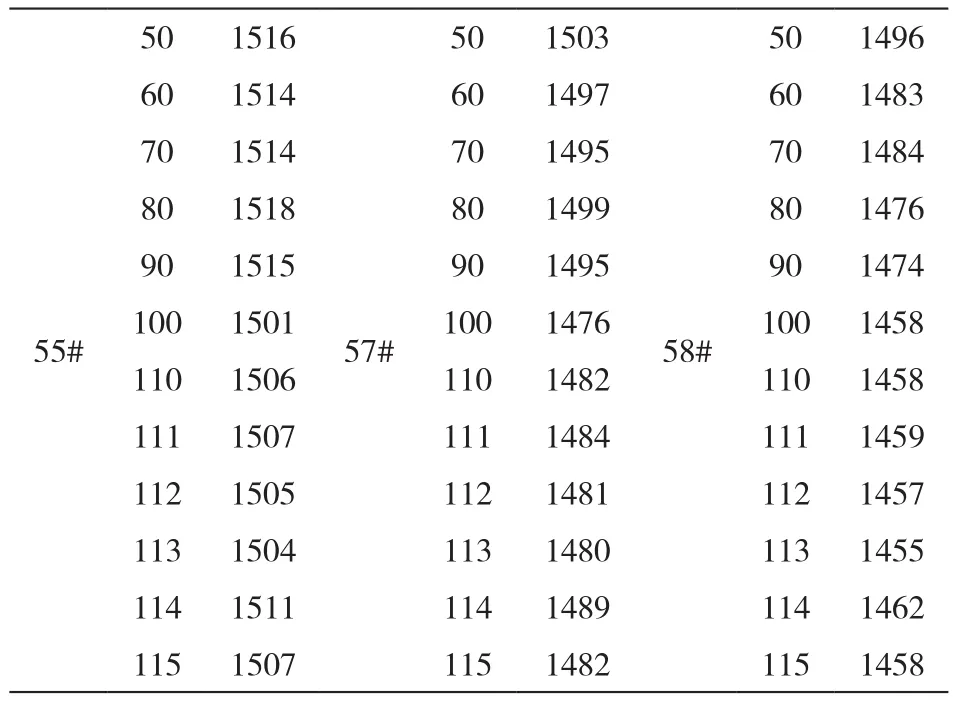
電池的部分充放電循環實驗結果如表1所示。

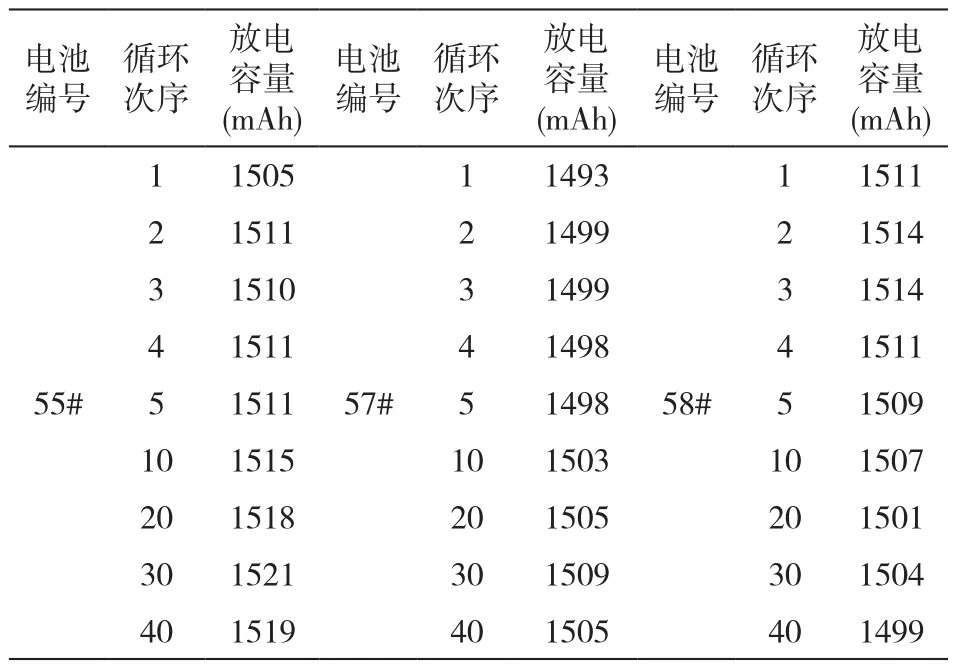
表1 部分充放電循環實驗結果

?

4.1 模型參數辨識

第115次充放電循環后，電池的恒流放電實驗數據如表2所示。

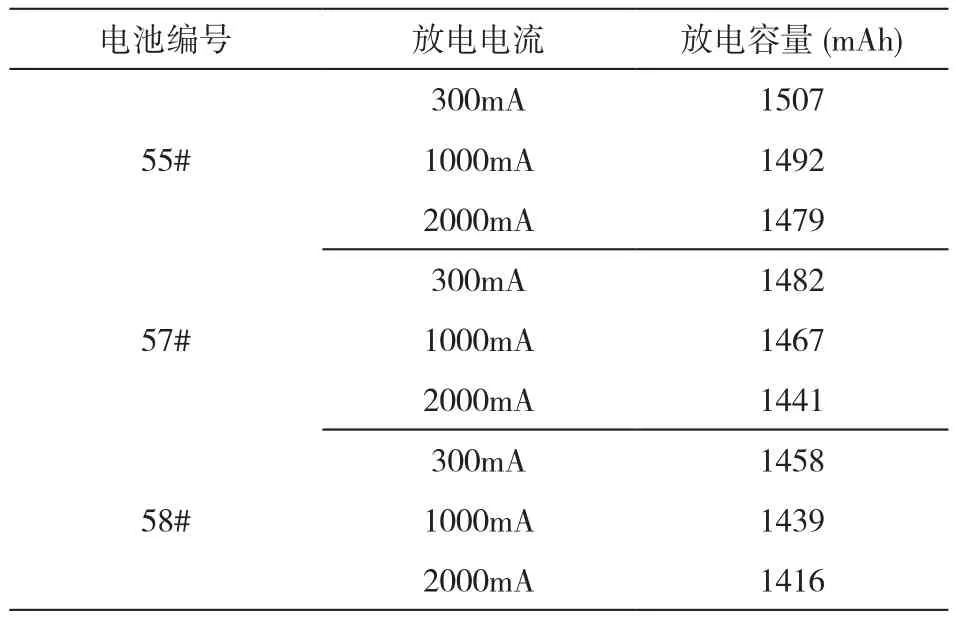
表2 第115次循環實驗后放電實驗數據

根據Peukert方程恒流放電容量預測模型，利用matlab的lsqcurvefit函數對上述實驗數據進行非線性擬合，得出表3。

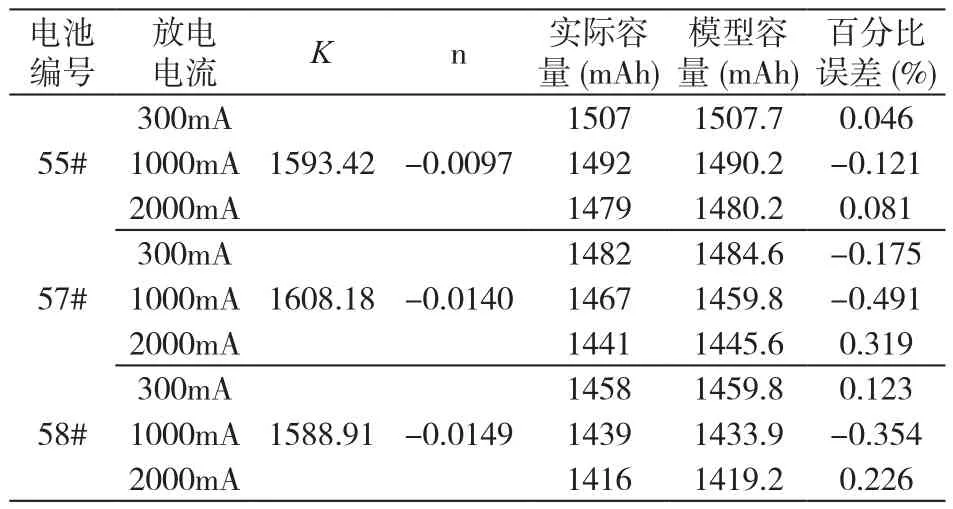
表3 Peukert方程擬合參數結果

根據Kinetic Battery Model（動力模型）容量預測方程(19)，同樣利用matlab的lsqcurvefit函數進行非線性擬合，得出表4。

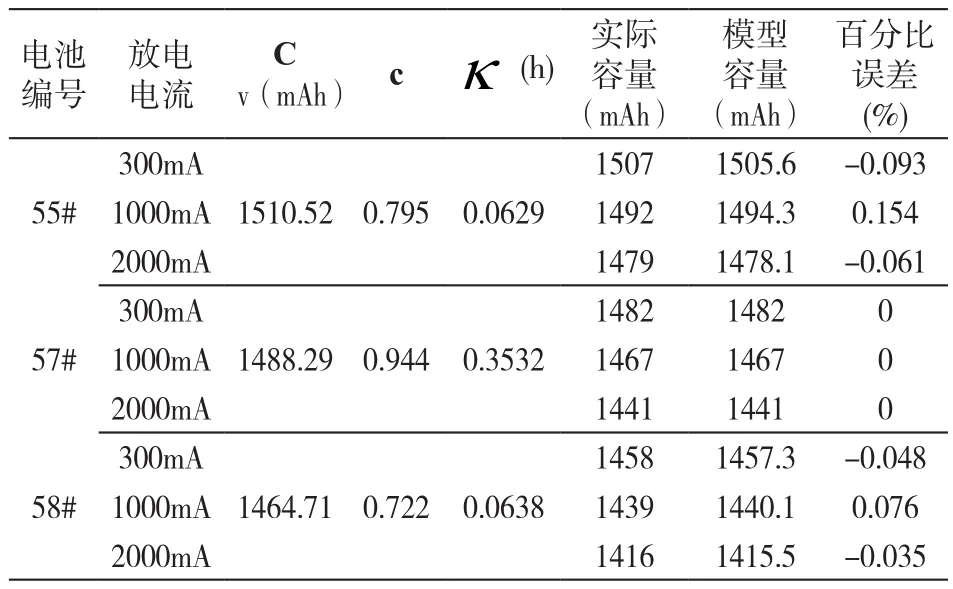
表4 Kinetic Battery Mode（動力模型）擬合參數

4.2 容量預測

根據參數辨識的結果，對充滿電靜置后（300mA恒流充電至3.65V——恒壓充電至電流小于10mA——靜置1h），不同電流恒流放電放出的容量進行預測，結果如表5所示。

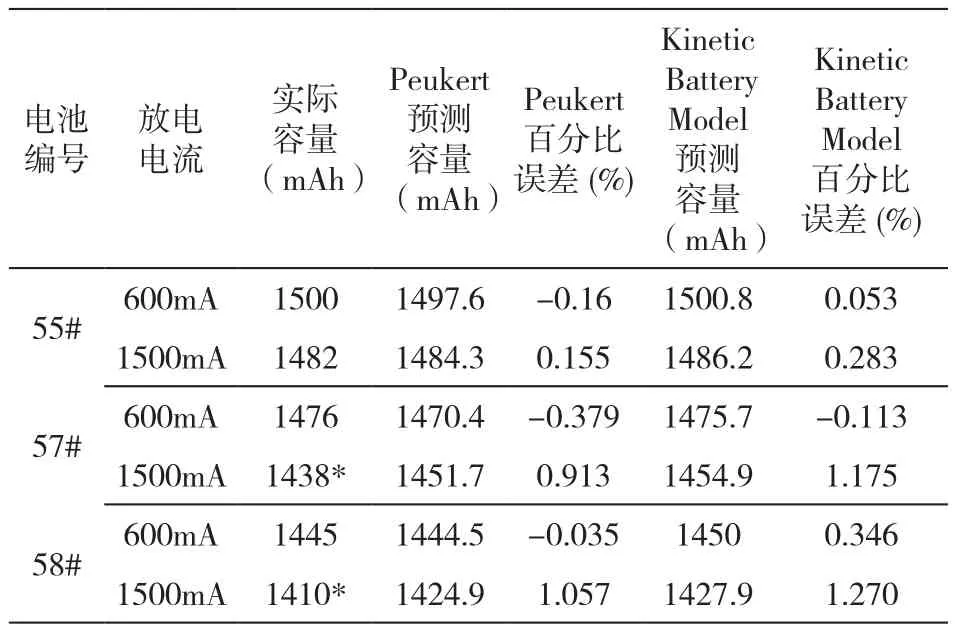
表5 Kinetic Battery Model與Peukert模型預測容量結果

5 結果分析

Peukert模型與Kinetic Battery Model（動力模型）對實驗數據的擬合與預測結果匯總如表6。

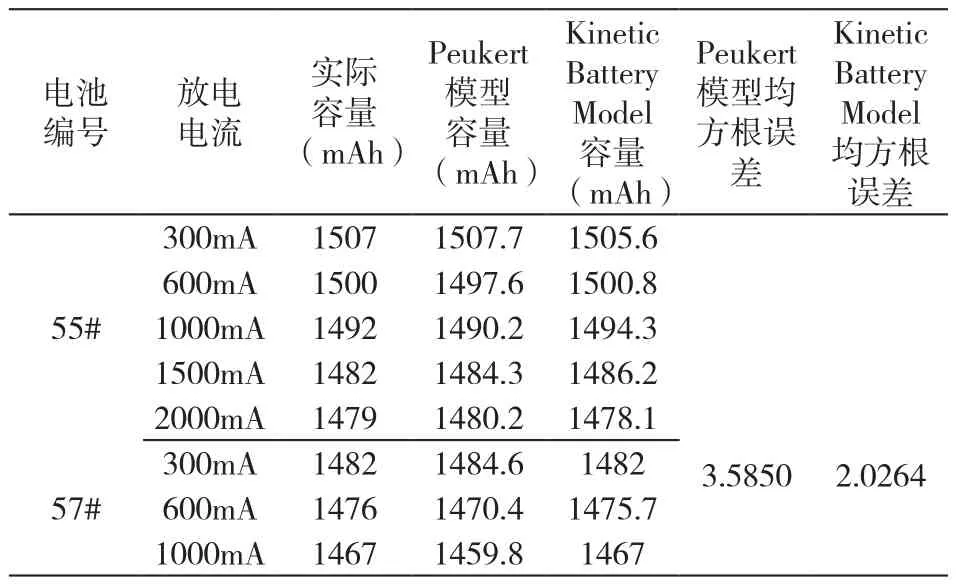
表6 Kinetic Battery Model與Peukert模型容量均方誤差比較

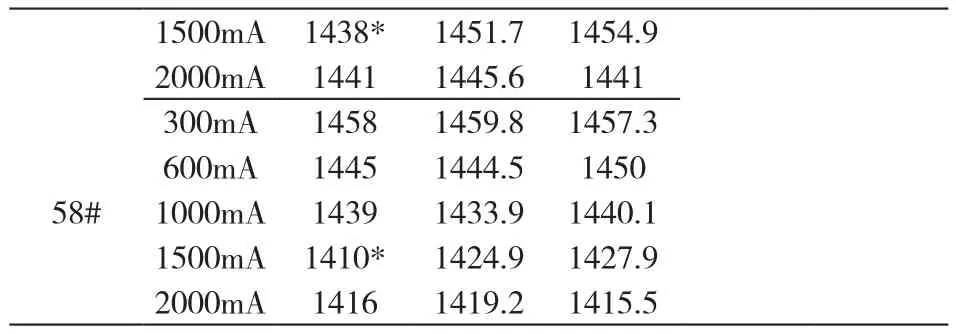
注：標“*”者為異常實驗值

表6中，57#、58#電池在1500mA恒流放電條件下的容量小于2000mA恒流放電條件下的容量，屬于異常值，出現異常實驗結果的原因可能與實驗結果的隨機性有關。根據表1顯示的部分充放電循環實驗結果，電池的放電容量并沒有表現出明顯的退化趨勢，而具有波動性（隨機性），每一次的放電容量可以看做一個隨機變量，歷次循環中電池的放電容量（隨機變量）的組合，就是一個隨機過程[4]，這些有待后續研究。如不考慮異常數據，通過表5對比，由Kinetic Battery Model（動力模型）做出的放電容量擬合、預測結果要優于Peukert模型的擬合、預測結果（均方根誤差較小）。

6 結論

本文利用Kinetic Battery Model動力模型對恒流放電條件下的電池容量做出了預測，并結合實驗數據，與Peukert經驗公式模型進行了對比，驗證了Kinetic Battery Model的可靠性。但本文尚未涉及模型參數隨循環使用次數增加而變化的規律。隨著實驗的深入， Kinetic Battery Model參數隨著電池循環使用的變化規律、Kinetic Battery Model參數與循環使用壽命的關系，將是下一步研究的目標。

[1] 王峰. 鋰離子電池電解液產業化進展[J].儲能科學與技術, 2016 , 5 (1) :1-8.

[2] Jongerden M. R. & B. R. Haverkort. Battery and the Kinetic battery model: A first exploration[J].International conference on anantitative Evaluation of Systems,2017,(4):88-103.

[3] Jongerden M. R. & B. R. Haverkort. Which battery model to use [C]. Applied Soft Computing，2011，11(2)：2556-2564．

[4] 顏景斌，王飛，夏賽.隱馬爾科夫模型預測電池健康度[J].哈爾濱理工大學學報, 2017, 22 (6) :33-38.