基于Shapley值修正的跨區域水電項目收益分配研究

曹文英，袁汝華

(河海大學商學院，江蘇 南京 211100)

2016年國務院發布了“十三五”攻堅扶貧計劃，強調可以通過水庫移民、修建水電工程等方式有效消除貧困，改善民生。在水電項目的開發過程中，跨區域水電項目的建設最為復雜，涉及眾多項目參與者。為了促進多方共同參與水電項目的開發，需對水電項目的收益進行合理劃分。本文根據“動態博弈”理論中的Shapley值模型，對水電項目跨區域建設過程中所得收益的合理分配進行研究，并結合實際情況，對模型進行修正，以確保各主體之間合作的順利進行。

目前，學者們對于收益分配理論的研究多聚焦于產學研、供應鏈和虛擬企業等領域。

a. 從產學研的角度對收益分配進行優化。劉云龍等[1]在研究如何對產學研領域中聯盟各方的收益進行分配時，提出先分析影響聯盟中收益分配方案的因素，再建模求出聯盟中各方的收益分配比例。梁喜等[2]引入多重系數，利用Shapley值法分析不同模式下的產學研聯盟收益分配狀況。李巍等[3]利用合作博弈的分析框架，建立初始狀態下的利益分配模型，對產學研協作共同體進行研究。張根明等[4]將控制權配置與再談判機制引入傳統產學研協同合作機制中，對技術價值不確定狀況下的利益分配進行最優化。陶丹等[5]在傳統博弈論模型中，加入縱向一體化、縱向合作和政府補貼優化路徑，對產學研收益分配進行對比分析。

b. 從供應鏈的角度對收益分配進行改進。Giannoccaro等[6]對供應鏈領域各企業之間的合作模式進行了分析，從中找出對該合作模式最終收益分配結果產生影響的各因素，并建立基于各因素基礎之上的方案模型。范德成等[7]探討了Shapley值法在造船供應鏈收益分配中的應用，并進行改進。房進軍等[8]基于文獻[7]，建立了Stackelberg博弈模型，對旅游供應鏈上不同企業的收益分配進行計算與協調。黃勇[9]利用Shapley值法對供應鏈上各合作者的貢獻度進行計算，提出并完善了目標價格制度與收益分配機制。常宏遠等[10]基于Shapley值法構建了供應鏈協同聯盟體的收益分配模型，降低了各主體間的不平等。

c. 從虛擬企業的角度對收益分配進行研究。王愚等[11]根據管理學和諧管理理論中的和諧度概念，利用Shapley值法改進了原有模型中無差異參與人的不足。包國憲等[12]基于“均衡性”與“功能性”原則，構建了適用于虛擬企業的收益分配指標體系。

綜上所述，有關跨區域水電項目領域中收益分配問題的研究較少，沒有形成一個主流、系統的收益分配方法。通過參考相關文獻，發現多數的收益分配方案考慮影響因素單一，建立的模型較為簡單，求解過程不夠嚴謹，不能廣泛應用在具體的項目案例中。基于以上情況，運用修正的Shapley值模型，擬定基于考慮眾多影響因素的跨區域水電項目收益分配方案，并用實例驗證，將理論與實際情況相結合，以期為相關研究提供理論參考，也為跨區域水電項目運行過程中涉及的收益分配問題提供解決方案。

1 影響跨區域水電項目收益分配的因素

在跨區域水電項目建設過程中，其項目的參與者包括多個政府部門以及社會企業，其中政府部門是主要的參與者，因此本文研究對象重點為兩個省市的政府部門。兩個省的政府部門既有合作的意愿又有利益方面的沖突。為了保證水電項目的順利運行實施，在對項目所獲收益進行分配時，有必要對影響收益分配的各主要因素進行分析。通過查閱相關的文獻，本著“風險與收益對稱”的原則，認為影響跨區域水電項目收益分配的主要有以下4個因素。

a. 投入比重。水電項目中的投入包括土地、水資源、資金、勞動力等要素。在項目實施過程中，各參與方的投入不僅影響項目整體的收益情況，也直接影響對各參與者最終利益和責任義務的分配。在其他影響因素不變的情況下，項目參與者在項目中獲得的收益應與其項目投入成正比[13]。

b. 風險分擔。跨區域水電項目建設周期較長，未知的風險也較復雜。結合跨區域水電項目在實際運營中遇到的風險并參考相關文獻，將風險分為五類，包括政治風險、市場風險等。在每一類風險下對應著多個細分的風險因素。分擔風險時，對于自身實力較強、能夠承受并把控風險的項目參與者，應多承擔一些項目的風險，相應地，也獲得更高的項目收益。

c. 價值貢獻。跨區域水電項目屬于大型公益工程，建設和使用跨區域水電項目過程中涉及諸多項目參與者，各項目參與者自身的能力和對項目運行實施的貢獻度不同。在項目周期內，水電項目可能產生發電、防洪、供水、航運、旅游等貢獻，有些貢獻僅針對特定的地區與人群(利益相關者)。為了確保項目的持續進行，有必要采用恰當的收益分配方法激勵各項目參與者做出必要的貢獻或犧牲，所以在擬定各項目參與者最終所能獲得的收益分配比例過程中，需要將價值貢獻度作為衡量標準之一。

d. 合同執行度。在跨區域水電項目的建設和運營期間，如果某一方不能很好地按照合同要求履行自身的義務，做出假公濟私等不道德行為，將使整個項目的收益受到影響，也會直接影響其他項目參與者最終所能分配的收益[14]。為了杜絕這種情況的發生，將參與者對合同的執行程度納入項目收益分配的考核指標中，激勵項目參與者在項目周期內采取積極有效的行為。

2 跨區域水電項目收益分配的Shapley值模型

Shapley值模型在博弈論中是一種普遍適用的、用于解決多個參與者之間合作問題的主流方法，依據貢獻度對各參與者的收益比例做出合理分配。本文主要研究跨區域水電項目中兩省通過合作所能獲得的最終收益分配比例，同樣適用于該模型。考慮到項目實際運行過程中其他影響收益分配的因素，對Shapley值模型進行補充完善，使其更貼合實際，可以有效地運用到跨區域水電項目的實踐中。

項目合作過程中，當各參與者采取的經濟活動沒有矛盾沖突時，參與者數目的增加也會帶來項目整體收益的增加。各參與者最終獲得的收益分配比例可以運用Shapley值模型根據各參與者對項目的價值貢獻度來確定[15]。定義如下：

a. 假設I={1,2，…，n}是項目中n個參與者的集合，I中任意一個子集s均有相對應的一個實值函數v(s)，符合以下條件：

v(φ)=0

(1)

v(s1∪s2)≥v(s1)+v(s2) (s1∩s2=φ,s1，s2?I)

(2)

b. 設v(i)為參與者i單干項目時所得的收益；φi(v)為參與者i選擇與其他參與者以合作方式開發項目所獲得的收益，滿足：

(3)

φi(v)≥v(i) (i=1,2,…,n)

(4)

則在集合I中各參與者最終獲得的收益為

φ(v)={φ1(v)，φ2(v)，…，φn(v)}

(5)

(6)

式中：si表示集合I中包含參與者i的所有子集；|s|表示子集s中的元素數量；v(s)表示子集s的整體收益。

3 Shapley值修正的跨區域水電項目收益分配模型

3.1 模型建立

運用Shapley值模型對項目收益進行分配是建立在考慮合作中各參與者對項目總收益的貢獻程度上的，在計算過程中，假設各參與者承擔的風險是一樣的，未考慮實際情況中風險等因素對收益分配比例的影響。將各參與者投入比重、風險分擔等因素納入收益分配方案的影響因素中，對Shapley值模型完善并修正，得到一個趨于合理、更符合實際的項目收益分配方案。

在對Shapley值模型進行修正過程中，影響收益方案的各因素構成集合L={j}，其中j=1,2,3,4，分別代表投入比重、風險分擔、價值貢獻、合同執行度等4個對項目收益產生直接影響的要素。假定在集合D中第i個參與者對第j個影響因素的修正測量值為aij，則4個因素經過修正后的測量值見表1。

表1 Shapley值修正的測量值

依據表1可知在跨區域水電項目中，對收益分配比例產生影響的4個因素測量值形成的系數矩陣A為

(7)

矩陣A歸一化之后，得到矩陣

(8)

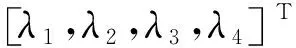
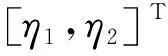
(9)

式中：η1，η2分別為4個影響因素對項目中兩省所能獲得收益份額的綜合影響系數。兩省分配到的最終收益為

(10)

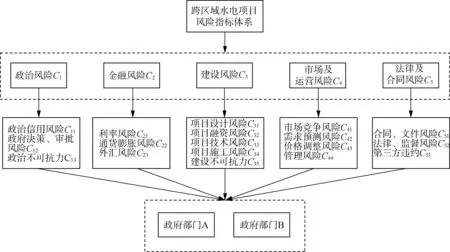
圖1 風險評價指標體系

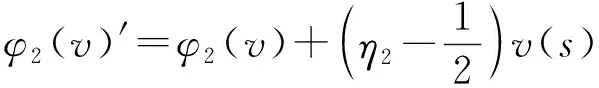
(11)

式中：v(s)為兩省合作開發跨區域水電項目所獲得的總收益。

3.2 參數的修訂過程

a. 投入比重向量的確定。計算兩省修建跨區域水電項目的投入不僅包括初始資金投入，還包含了修建過程中追加的資金，以及其他資本的投入，如人力、土地等。對于投入比重的確定，很難以準確的數值衡量，在雙方合作之初，需要通過協商來確定投入比重向量a11、a21。

b. 風險分擔向量的確定。構建風險評價指標體系，在體系構建過程中通過層次分析法對每一層指標確定權重，請相關專家對每層風險因素打分，從而得到跨區域水電項目中兩省政府部門對于項目風險的分擔向量，分別為a12，a22。風險評價指標體系構建見圖1。

計算過程中，將跨區域水電項目中兩省政府承擔的風險因素劃分為五類，列為二級指標，記為Ci(i=1,2,…,5)；再將每一類二級指標Ci細分為三級指標，列出每一類二級指標下的子風險因素，記為Cij(i,j=1,2,…,5)。構建指標體系后請專家兩兩比較每一層風險因素相對重要程度后打分，分值取為1～9，1代表該風險因素對項目影響極小，3代表影響較小，5代表影響一般，7代表影響較大，9代表影響極大。進而確定Ci所含低層風險因素相對于Ci的權重，以及Ci的權重向量，依此類推，最終得到跨區域水電項目中兩個政府部門的風險分擔向量。

c. 價值貢獻向量的確定。跨區域水電項目中兩省政府部門對該項目運行實施所貢獻的價值，也被納入項目收益分配方案的影響因素。價值貢獻度主要反映兩省政府部門對項目的積極性，價值貢獻指標的確定可以請專家打分。兩省的貢獻向量分別為a13，a23。

d. 合同執行度向量的確定。合同執行度的評判主要依據兩省政府部門按照合同規定完成任務的進度情況。可以邀請專家或獨立的第三方對項目的任務進度情況打分，進而確定兩者的合同執行度向量a14，a24。

e.λ的確定。鑒于每個項目的外在和內部環境不一樣，不同的收益分配影響因素對項目的影響程度也不一致。如在偏遠落后地區，投入比重對項目最終收益分配方案會產生更大的影響，因此，對于綜合影響系數矩陣λ的確定，需要因時、因地制宜。本文采用專家打分法確定λ。請相關人員對4個因素進行評分，再對打分表匯總整理以及歸納，最終確定λ。

4 實例應用

4.1 工程概況

黑山峽河段地處中國西部甘肅省和寧夏回族自治區的交界地帶，是最后一個可以在黃河上游地區建造峽谷高壩大庫的河段，在該河段修建水電項目可以響應國家2016年12月提出的“十三五”脫貧攻堅計劃，改善西北地區的貧困局面。因對河段開發的功能定位和收益分配方案的認識不完全統一，尚未對黑山峽河段的開發方案做出決策。河段目前的開發方案傾向一級開發方案。本文就一級開發方案對寧甘兩省(區)的收益分配問題進行有針對性的分析，以期為寧甘兩省(區)及有關部門對黑山峽河段開發達成共識提供基礎和支撐[16]。

在一級開發方案中，項目全生命周期為57年(建設期7年，生產期50年)。在第6年年底，項目逐漸投入使用。生命周期內累計稅后利潤，即兩省合作開發項目所獲得的總收益v(s)為357.76億元，若由寧夏單獨負責項目建設運行，需要補償甘肅因水庫淹沒帶來的損失，即v(1)為198.26億元。而由甘肅單獨負責項目建設運行所帶來的收益等于四級開發方案整體收益扣除方案中建設寧夏大柳樹低壩電站帶來的全部收益和小觀音低壩的一半收益，即v(2)為140.09億元。

4.2 運用Shapley值模型的收益分配方案

由式(6)可知寧甘兩省(區)在此次共同開發水電項目中所分配到的利潤分別為：φ1(v)=207.97億元；φ2(v)=149.80億元，即寧夏可以獲得利潤207.97億元，甘肅可以獲得利潤149.80億元。通過對比兩省合作前后各自獲得的收益，可以看出合作后收益均有一定幅度的增加，說明兩省合作開發該水電項目的必要性。

4.3 運用修正Shapley值模型的收益分配方案

考慮影響收益分配的各因素，對兩省獲得的初始收益數值進行補充完善，得到最終的收益分配數值。

投入比重向量的確定。根據兩省在合作過程中對資金、物力、人力等的投入，經雙方協商確定寧夏區所占投入比重a11為0.58，甘肅省所占投入比重a21為0.42。

風險分擔向量的確定。利用層次分析法以及請專家打分評價可得兩省在合作中的風險分擔向量a12、a22分別為0.55、0.45。

價值貢獻向量的確定。鑒于合作雙方在該水電項目建設過程中均需依據合同規定盡力完成項目建設，同時應對某些未知狀況的發生，所以無法精確衡量其貢獻度，假設兩省貢獻相同，a13、a23均為0.5。

合同執行度向量的確定。需要在該水電項目完工之后做出評價，檢查兩省是否嚴格依據合同規定完成相應的任務，暫定兩省在項目建設過程中均嚴格按照合同的各項規定，即a14、a24均為0.5。

λ的確定。依據各專家對4個因素的重要程度進行打分，結合在項目施工過程中的實踐經驗，最終確定各因素的重要程度，得出4個影響因素對該水電項目的影響向量λ=(0.4，0.25，0.15，0.2)T。

依據式(7)可知，跨區域水電項目中對項目的收益分配方案產生影響各因素構成的矩陣A為

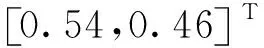
在確定η1，η2后，根據式(10)、(11)確定兩省分配的最終收益為：φ1(v)′=222.28億元；φ2(v)′=135.48億元。

5 結 論

跨區域水電項目的建設涉及多方利益博弈。為了保證項目順利實施，本文運用修正Shapley值模型對項目收益進行合理分配，實例驗證并得出以下結論：

a. 運用修正Shapley值模型的收益分配方案體現公平合理原則。根據Shapley值理論，收益分配主要依據各參與者對項目的貢獻，忽略了項目實際修建運營中各參與者對風險的承擔以及各種資金與非資金投入等。在項目實際建設運行中，合作雙方對于風險承擔的能力和比例不盡相同，對項目的投入和對合同的執行力度也不一樣，將投入比重等其他三方面因素列入收益分配方案的考核因素中，可以使分配方案趨于公平合理。

b. 運用修正Shapley值模型的收益分配方案可以有效促進各參與者采取積極措施投入項目建設中。通過案例可以看到，各參與者選擇合作開發水電項目可以增加項目整體收益，且采用Shapley值模型的收益分配方案可以使各自所獲項目收益比之前有顯著增加，這樣就會促使各參與者為了謀求自身和項目整體收益而尋求合作者，選擇最佳的合作方式；另外，在收益分配方案中考慮諸多因素的影響也可以激勵各參與者采取更積極的態度和方法來參與項目建設，促進各參與者加大對項目的資金和技術投入，管理手段更加多樣性，以更積極的態度和更好的解決方案應對項目過程中的風險。因此，筆者認為在跨區域水電項目的合作中運用修正Shapley值模型來制定項目最終的收益分配方案具有優越性。

參考文獻：

[1] 劉云龍，李世佼. 產學研聯盟中合作成員利益分配機制研究[J]. 科技進步與對策，2012，2(3)：23-25.

[2] 梁喜，馬春梅.合作創新與利益分配比例對產學研聯盟利潤的影響[J].科技進步與對策，2015，5(16)：21-28.

[3] 李巍，花冰倩.合作博弈框架下產學研協同創新的利益分配策略研究：社會網絡分析視角[J].商業研究，2016，62(9)：39-45.

[4] 張根明，楊思涵.技術入股型產學研合作創新的利益分配研究：基于技術價值不確定性的新視角[J].軟科學，2017(10)：1-5.

[5] 陶丹，朱德全. 產學研協同創新中產出分享利益分配方式的優化路徑[J].統計與決策，2017(7)：36-40.

[6] GIANNOCCARO I，PONTRANDOLFO P. Supply chain coordination by revenue sharing contracts[J].International Journal of Production Economics，2004，89(2)：131-139.

[7] 范德成，胡鈺.造船供應鏈利益分配問題的Shapley值法分析[J].哈爾濱工程大學學報，2014(5)：649-653.

[8] 房進軍，劉玲.基于Shapley值法的旅游供應鏈利益分配[J]. 物流技術，2015，34(16)：114-117.

[9] 黃勇.基于Shapley值法的豬肉供應鏈利益分配機制研究[J].農業技術經濟，2017(2)：122-128.

[10] 常宏遠，鄧蕾，涂志剛. 基于合作對策的三級逆向供應鏈利益分配[EB/OL].北京：中國科技論文在線[2017-04-07]. http：//www.paper.edu.cn/releasepaper/content/201704-71.

[11] 王愚，陳冬梅，張小敏.基于和諧度的虛擬企業利益分配策略研究[J]. 江蘇科技大學學報(自然科學版)，2010，24(3)：294-297.

[12] 包國憲，王學軍，柴國榮.虛擬企業的利益分配與協調研究[J]. 科技進步與對策，2012，29(24)：123-126.

[13] 白紅飛，王剛. PPP收益分配模型研究[J]. 合作經濟與科技，2015(10)：72-74.

[14] 方茜，陳菁，代小平，等. 基于合作收益的跨區域水源保護補償額測算方法研究[J]. 水利經濟，2011，29(2)：38-40.

[15] 樊亮. 基于Shapley值修正的PPP項目利益相關者收益分配研究[D]. 天津：天津大學，2014.

[16] 朱軍. 中國水力發電史：1904—2000 第3冊[M]. 北京：中國電力出版社，2007.