導葉數目對兩級動葉可調軸流風機葉片靜力結構及振動的影響

劉宏凱， 葉學民， 范福偉， 李春曦

(電站設備狀態監測與控制教育部重點實驗室 (華北電力大學)，河北 保定 071003)

0 引言

動葉可調軸流風機以其高效和易調節等優點已成為燃煤發電機組的送、引和一次風機的首選。葉片是軸流風機的核心部件，決定風機的性能；而導葉是軸流風機中重要的流通部件，其氣動設計直接影響上下游流通部件的特性。研究表明，葉輪機械內的流固耦合現象與流體機械各種故障的產生有直接關系[1～4]。因此借助流固耦合的方法對導葉數目變化后風機葉片的靜力結構及振動進行研究具有重要的現實意義和工程價值。

導葉結構、數目和安裝角度對提高流體機械的性能、降低噪聲和減輕振動具有明顯影響。李忠等[5]利用試驗對軸流泵有無導葉時的外特性進行測試，表明在最優工況下導葉可回收的旋轉動能約占葉輪出口總能量的15.7%，驗證了導葉對提高能量利用率的作用。張德勝等[6]模擬導葉數目不同時泵內的壓力脈動特征，指出導葉數變動對導葉區流域及其下游流域的壓力脈動具有一定影響,而對上游葉輪流域的流動影響則較小。石亞君等[7]利用數值模擬方法對導葉與葉輪匹配進行研究，表明導葉數目增加后模型壓力提高329 Pa，軸功率降低1.2 kW，效率提高6%。孟麗等[8]模擬了軸流風機后導葉改變對風機性能的影響，表明導葉數目減少4片后全壓提升5.4 Pa，效率提高0.8%。葉學民等[9]利用模擬方法分析了第一級導葉結構形式對某兩級動葉可調軸流風機性能的影響，表明長短復合導葉對提升軸流風機氣動性能方面好于單一長度葉片式導葉。

在流固耦合模擬研究方面，吳正人等[10]利用CFX和Ansys對離心風機葉輪的模擬表明，風機氣動性能基本不變，而最大變形量減少2.5%，最大等效應力增大3.6%。張磊等[11]研究了失速工況下葉輪的靜力特性，指出氣動力載荷對葉輪的總變形量有顯著的影響，對葉輪等效應力分布的影響較小。羅黎等[12]分析了軸流風機旋轉工作時的應力及總應變，驗證了在流固耦合作用下風機工作的強度要求。Dhopade[13]模擬了低周疲勞與高周疲勞聯合作用對燃氣輪機葉片結構與氣動性能的影響。毛軍等[14]在考慮葉片和流域相互耦合狀態下，對大型軸流風機葉片的氣動彈性的模擬表明，考慮氣動彈性的最大應力幾乎是不考慮氣動彈性的最大應力的兩倍，由此證明在葉片安全性評估方面考慮氣動彈性的必要性。

綜上所述，目前對于軸流風機的導葉數目改變研究只關注其氣動性能，而對于葉輪靜力結構和振動情況研究較少。因此，本文研究對象為某電廠660 MW機組配套的動葉可調軸流一次風機，借助Fluent軟件對其內部流場進行數值模擬，并借助Workbench流固耦合模塊對葉片進行靜力分析和預應力下的模態分析，對導葉數目改變前后的葉輪安全性進行評估，為風機生產和改造提供參考依據。

1 風機模型

1.1 物理模型

某600 MW機組配套的兩級動葉可調軸流一次風機，其內部結構如圖1所示。流體計算域包括從集流器到擴壓器的內部通道，固體計算部分為葉輪葉片部分。其主要參數如表1所示，原風機每級導葉數目為23片，改造方案圍繞導葉數目進行。風機動葉片和導葉片數目通常是互質的，可以減少上游氣流對下游的沖擊，減少氣流脈動及噪聲。改造方案成組減少或者增加導葉片，如表2所示，其中導葉數目減少為方案一至方案三，導葉數目增加為方案四至方案六。

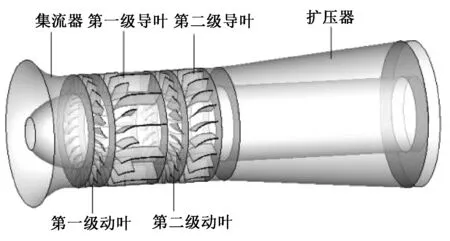
圖1 軸流風機模型圖

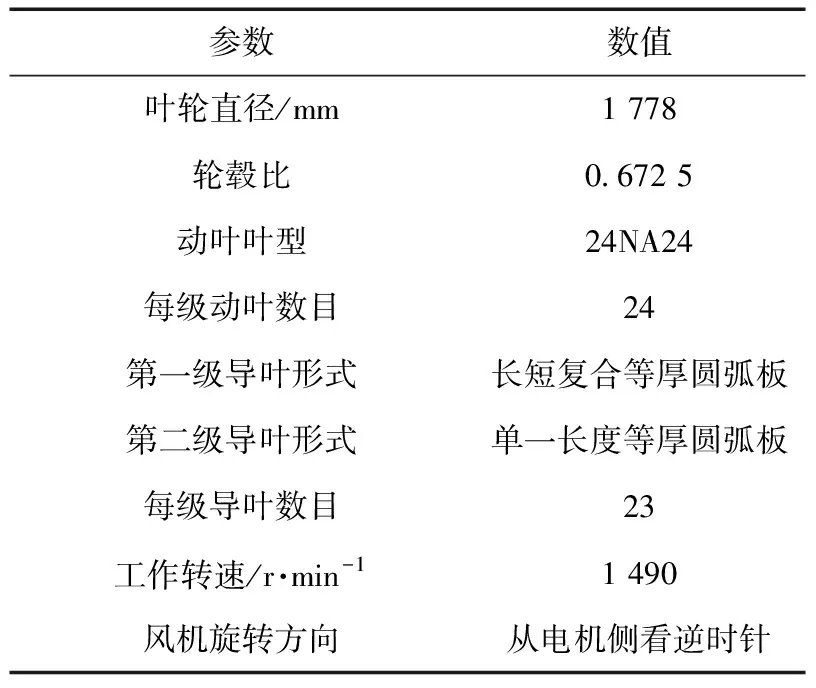
參數數值葉輪直徑/mm1 778輪轂比0.672 5動葉葉型24NA24每級動葉數目24第一級導葉形式長短復合等厚圓弧板 第二級導葉形式單一長度等厚圓弧板每級導葉數目23工作轉速/r·min-11 490風機旋轉方向從電機側看逆時針

表2 導葉數目改造方案

1.2 網格劃分和邊界條件設置

1.2.1 流域邊界條件設置

基于軸流風機軸向可以分區的結構特點，采用分區法將流體計算區域劃分為集流器區、第一級動葉區、第一級導葉區、第二級動葉區、第二級導葉區和擴壓器等6個部分，因為動葉區內流動最為復雜，故采用尺寸函數對動葉區進行加密，而其他區域采用較為稀疏的網格。在模擬中進行了網格無關性驗證，分別采用260萬、380萬、560萬和820萬等網格數對風機氣動性能進行計算，在保證較好的計算精度和計算成本的前提下，確定網格數為560萬，在此網格數下時間成本和模擬精度最好。運動方程為三維定常雷諾時均N-S方程，采用可有效解決旋轉運動和二次流的Realizablek-?湍流模型[15]，動葉區采用多重參考系模型。在數值模擬中，以集流器入口和擴壓器的出口作為整個計算域進出口，邊界條件為進口速度和自由流出。進出口流量殘差小于10-5，各方向的速度及k、?等參數的殘差小于10-4，認為當前計算達到收斂要求。

1.2.2 葉片結構模型

圖2為軸流風機動葉輪及動葉片模型，其材料力學性能如表3所示。

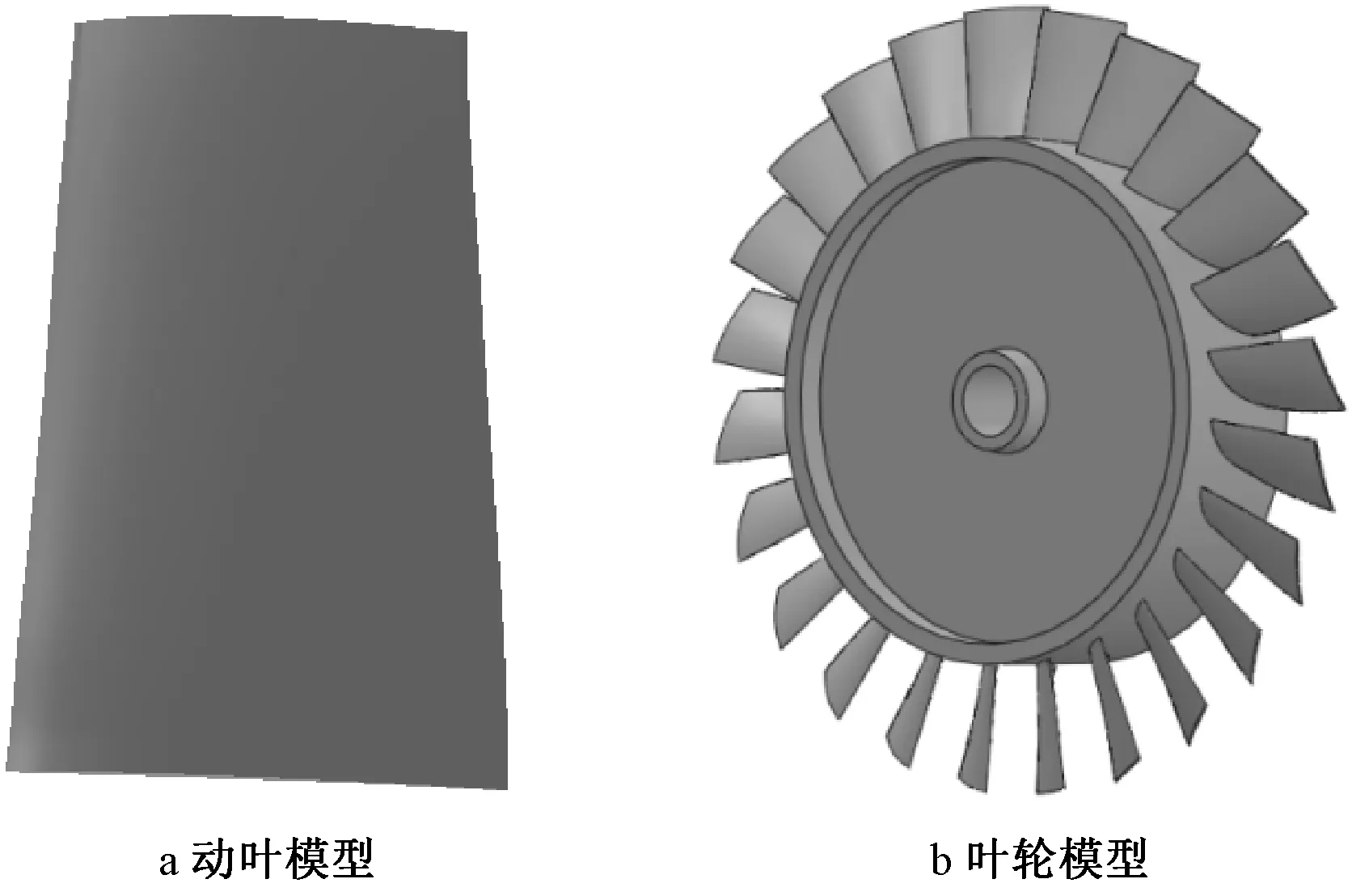
圖2 動葉輪及動葉片模型

名稱 密度/(g/cm3)彈性模量泊松比屈服強度/MPa ZL1012.66 6.9×10100.31180

由于動葉片是扭曲葉片，網格單元選用帶含有10個中間節點的四面體實體單元Solid187。分別采用20萬、30萬、55萬和60萬網格計算后，選擇設定單元大小15 mm，生成網格單元數量為30萬、節點數量45萬，在計算時間和計算精度上最為合適。對葉片葉根部位施加固定約束，葉片整體施加離心力慣性載荷，對葉片表面施加氣動壓力載荷，其中氣動壓力載荷是流體計算得到的壓力數據，采用流固弱耦合的方式加載到葉片表面，其加載流程圖如圖3。

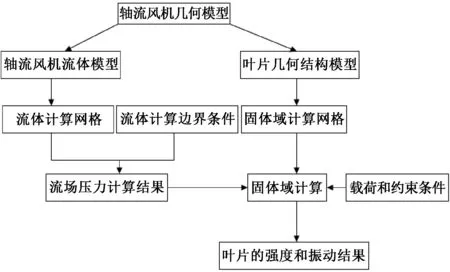
圖3 弱耦合計算流程

1.3 數值模擬的準確性

為驗證模擬結果的準確性，圖4將模擬結果與試驗樣本值進行對比。圖4中P表示風機全壓，η表示風機效率。結果顯示，在模擬風機運行范圍內，模擬所得全壓、效率與試驗樣本值的平均偏差分別為4.2%、 1.8%，特別是在設計流量下為3.4%和2.2%，由此可確保數值模擬的真實可靠性，模擬結果可反映該風機的實際運行狀況，并且可以用于進一步固體域的流固耦合模擬計算。

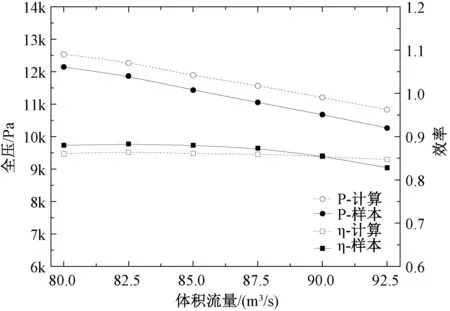
圖4 模擬結果與樣本曲線對比

2 計算結果和分析

2.1 性能影響

表4是導葉數目變化后的風機性能。導葉數目改變后整體上不影響風機性能的變化趨勢，全壓隨流量增大而減小，效率呈現先增后減的變化。如表4所示，qv表示風機體積流量，導葉數目減少時，在qv<90 m3/s時全壓均得到提高，在高于此流量時僅方案二全壓低于原風機，其中在導葉數目減少后，流量越小提升作用越明顯，方案三在qv=80 m3/s時，全壓提升效果最明顯，提升數值為141 Pa。導葉數目增加時，在qv<85 m3/s時，方案四至六全壓得到有效提升，而qv>85 m3/s時，僅有方案四全壓得到提升。導葉數目減少時風機效率明顯高于導葉數目增加時的風機效率；在導葉數目減少的方案中，在qv<87.5 m3/s時全壓全部高于原風機，在高于此流量時提升效果僅方案二比原風機效率稍高，其余方案略低于原風機，在設計流量82.5 m3/s時，方案三的效率提升效果最好，提升比例為0.46個百分點；在流量低于設計流量時，方案四至六效率高于原風機，高于設計流量時風機效率低于原風機，且隨流量增大，效率下降速度加快。從性能比較上可以看出，方案三表現出優于原風機的性能，所以下文主要針對方案三和原風機進行流固耦合模擬研究。

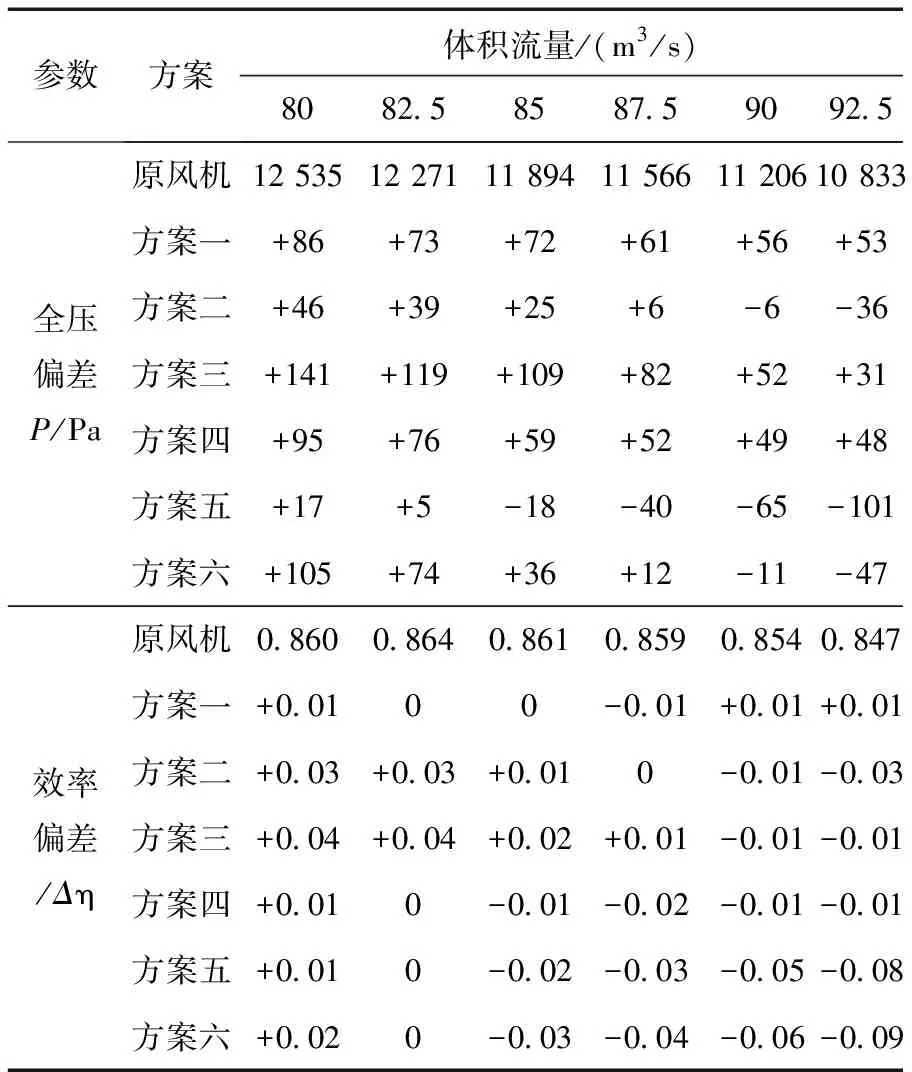
表4 改造后風機的性能對比

軸功率Psh定義為單位時間內原動機傳遞給風機軸上的能量，其大小可反映風機的能耗[16]。因此導葉數目改造對于經濟性的影響可通過軸功率來考察，圖5為原風機和方案三軸功率比較。從圖可以看出方案三比原風機軸功率有少許增加且變化不大，這也與方案三全壓提升做功能力增強有密切關系。

圖5 原風機和方案三軸功率

2.2 靜力結構特性

在旋轉機械中，葉片結構強度和振動直接關系到其安全運行，其取決于葉片表面的氣動載荷和本身固有的力學性能。而僅對流體域進行研究還不能完全確定導葉數目變化是否對風機固體域產生影響，為此利用ANSYS Workbench軟件將流場壓力數據加載到動葉片表面，對風機動葉進行了單向流固弱耦合，來研究導葉數目變動后動葉等效應力、總變形及振動的變化。

加載氣動力、離心力后計算得到導葉數目變化后動葉的應力基本沒有影響，動葉吸力面的近葉頂部位等值線沿葉高方向近似呈倒S分布且應力較小；葉根部分布應力較為復雜，最大值位于葉根中部與輪轂接觸位置，此處是由于承受較大的徑向離心力、垂直于葉片表面的氣動力和扭曲的葉型結構共同作用造成；第一級等效應力稍微高于第二級等效應力，這是由于離心力沿徑向，而氣動力垂直于葉片表面，氣動力的作用效果抑制離心力作用效果造成的，但氣動力作用效果影響較小；總變形近似沿對角線方向由小到大發生變化，葉根處變形基本為零，最大值變形位于葉頂后緣。由此可知導葉數目變化后，對葉片總變形基本沒有影響。圖6和圖7給出了改造前后風機葉片應力及總變形。

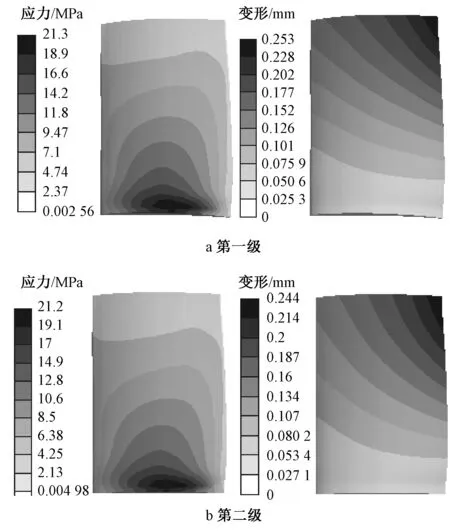
圖6 原風機動葉片應力及總變形

在靜應力強度分析中，通常選取材料的屈服極限作為極限應力，基于第四強度理論對葉片進行強度校核[17]。塑性材料的許用應力[σ]=σs/ns,其中σs是材料的屈服極限，ns為材料的安全系數，一般對于彈性結構材料加載靜力載荷的情況下，ns=1.5～2。葉片材料為ZL101，其屈服強度σs=180 MPa,ns=2，計算葉片的許用應力為90 MPa，而葉片最大等效應力的峰值為21.3 MPa，遠小于葉片許用應力，因此改型后方案三強度仍滿足要求。在葉片剛度方面，前面分析知，氣動力作用效果對離心力效果有抑制作用[18]，方案三全壓相對于原風機有所增大，最大變形有所降低，這與圖6和圖7一致，剛度更能滿足目前的使用要求。

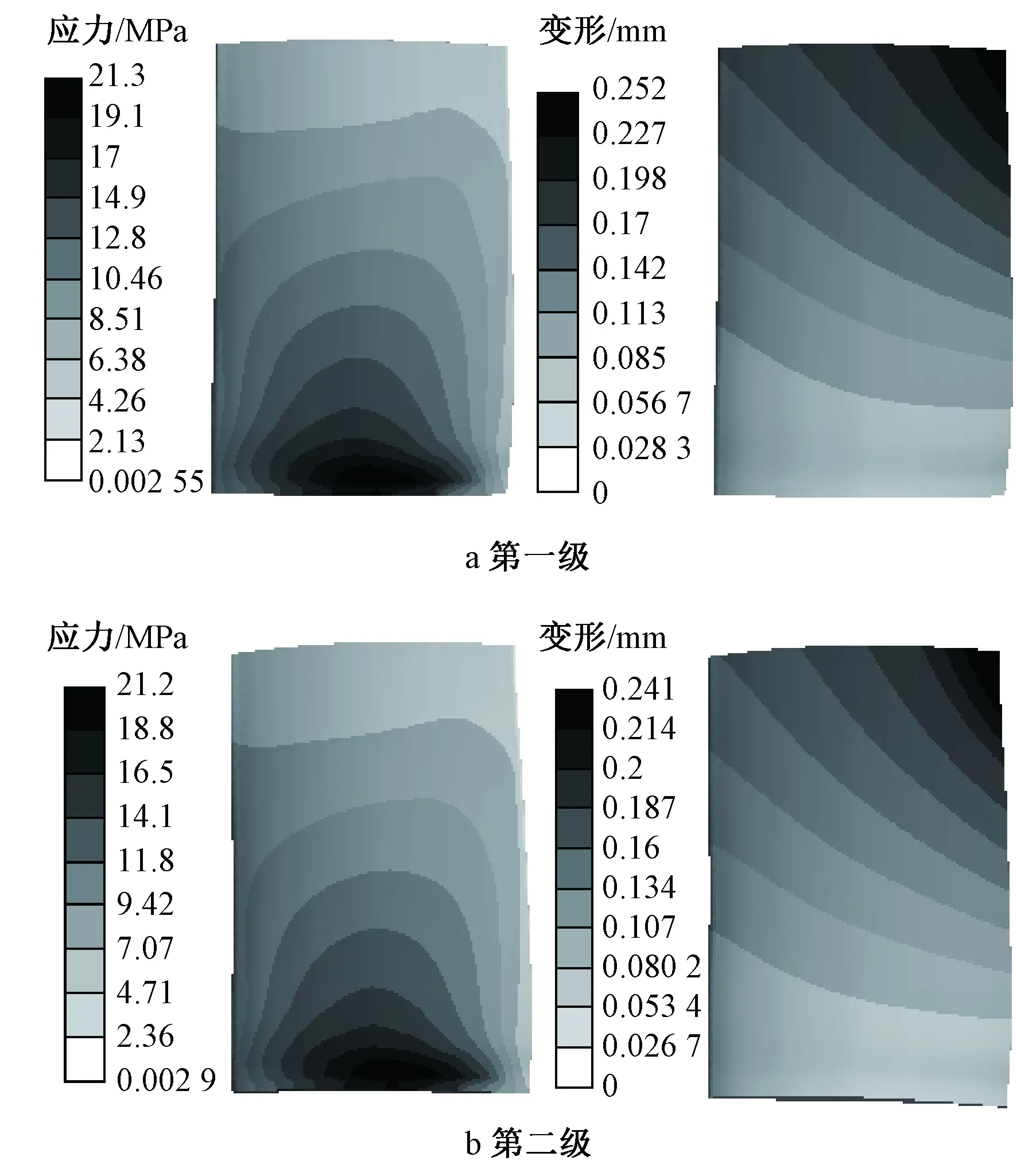
圖7 方案三動葉片應力及總變形

2.3 模態分析

葉片是軸流風機的最核心部件，在振動作用下容易發生破損或斷裂，對葉片進行振動分析具有重要的工程意義。模態分析主要是分析結構的振動屬性，葉片的固有特性包括頻率和模態振型，與葉片的質量和剛度分布有關。

表5列出了葉片在預應力下的前六階振動頻率。第二級動葉區的全壓數值上基本是第一級的兩倍且流體流動更加復雜，兩者離心力慣性力相同，在同等條件下第二張動葉區更容易發生損壞，而第一級與第二級各階的固有頻率基本一致，所以離心力對固有頻率起決定性作用，氣動力對固有頻率影響較小。葉輪各階模態的臨界轉速為n=60f,可得到各階模態的臨界轉速。通常情況下，一階臨界轉速下的振動最為激烈，葉片的一階臨界轉速為16 860 r/min，而工作轉速為1 490 r/min，遠比一階臨界轉速低，因此不會產生共振，滿足風機的設計使用要求，同時方案三風機振動頻率基本沒有發生變化，也滿足使用要求。

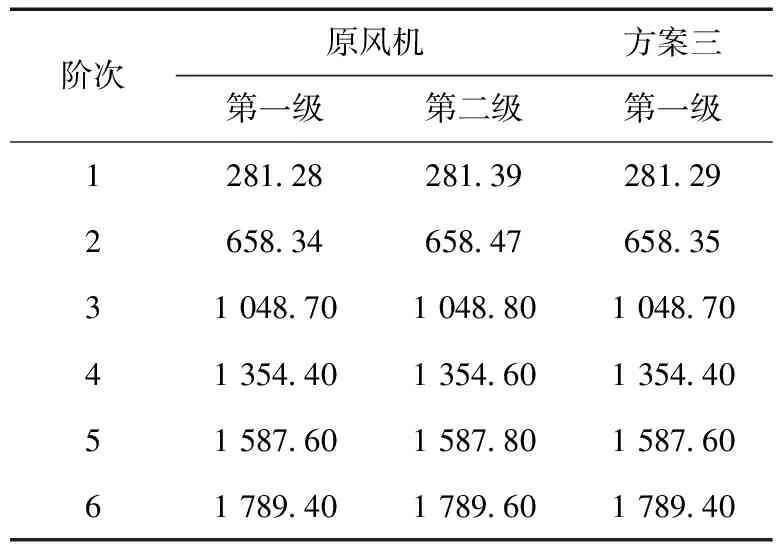
表5 改造前后動葉片前六階固有頻率 Hz

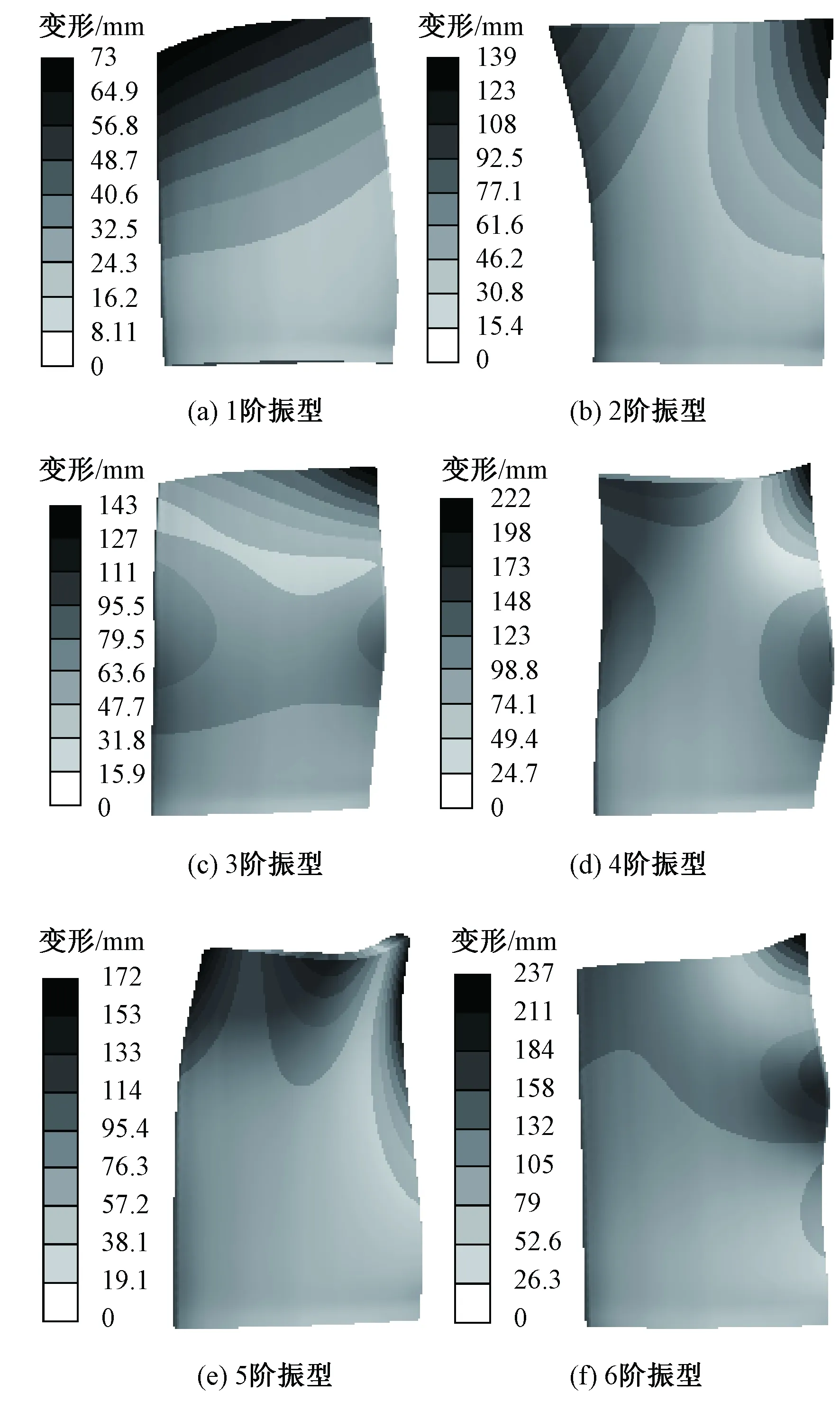
圖8 原風機第二級動葉片前六階振型

圖8和9為第二級葉片前六階振型圖。

由圖可知，導葉數目改變前后葉片振型基本沒有發生變化，在葉片的前緣或者后緣點處現振動最大位移，葉根部位振動位移較小。第1階振型為葉片前緣點繞軸向的彎曲振動，第2階振型為葉片前、后緣點繞軸向的扭轉振動，第3階振型為葉片后緣點繞軸向的扭轉振動與一階彎曲振動的復合運動，第4階振型為葉片后緣點繞軸向扭轉與一階彎曲振動的復合振動，第5階振型為扭轉與一階彎曲振動的復合振動，第6階振型為葉片后緣點繞軸向的二階彎曲振動。圖9可以看出，隨模態階數的依次增加，葉片各階振型變得更加復雜，葉片的高階次振型變為葉片復雜彎曲與繞軸扭轉的復合振動。

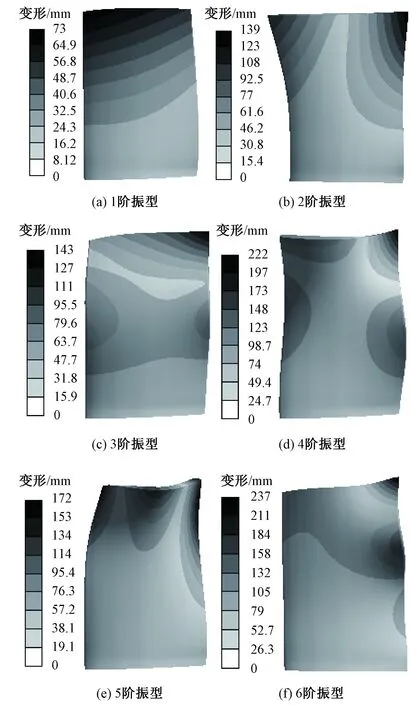
圖9 方案三第二級葉片前六階振型

3 結論

(1) 導葉數目減少后風機性能明顯優于導葉數目增加后風機性能，其中兩級導葉數目均為21片的方案三性能最佳，全壓效率均得到有效提高，同時改型后軸功率小幅度增加，方案三耗電量有所增加。

(2) 將流場計算數據加載到固體域表面后，應力、總變形和固有頻率基本不變，離心力對葉片的強度和振動起決定性作用，而氣動力對其影響較小；葉片的工作轉速遠低于一階臨界轉速，不會發生共振。

(3) 綜合考慮方案三的風機性能、軸功率、強度和振動分析結果，以及減少一組導葉也可降低設計制造成本，可知減少導葉的方案三對實際生產和改造具有一定參考意義。

參考文獻：

[1] 張磊, 楊維波, 梁守方, 等. 葉輪機械流固耦合問題研究進展[J]. 熱力發電, 2014,43 (12): 1-8.

[2] 張同桐, 何奕為, 黨冰潔, 等. 基于Solidworks軟件的閉式葉輪強度分析[J]. 風機技術, 2017, 59(2): 43-47.

[3] 楊夢迪, 施康. 某高轉速地鐵風機強度、振動數值分析和優化設計[J]. 風機技術, 2016, 58(6): 40-44.

[4] 王松嶺, 孫哲, 吳正人, 等. 基于流固耦合的離心通風機葉輪強度研究[J]. 華北電力大學學報(自然科學版), 2011, 38(4): 81-85.

[5] 李忠, 楊敏官, 王曉坤. 導葉對軸流泵性能影響的試驗[J]. 排灌機械, 2009, 27(1): 15-18.

[6] 張德勝, 施衛東, 王川, 等. 斜流泵葉輪和導葉葉片數對壓力脈動的影響[J]. 排灌機械工程學報, 2012, 30(2): 167-170.

[7] 石亞君, 葛愛香, 付艷霞, 等. 基于CFD方法的離心風機葉輪和導葉的改型分析[J]. 風機技術, 2017, 59(6): 27-31.

[8] 孟麗, 林麗華, 吳海英, 等. 軸流風機后導葉三維數值優化設計方法及其應用[J]. 風機技術, 2014, 56(3): 48-52.

[9] 葉學民, 李新穎, 李春曦. 第一級導葉改進對兩級動葉可調軸流風機性能的影響[J]. 動力工程學報, 2014, 34(3): 228-235.

[10] 吳正人, 王松嶺, 戎瑞, 等. 基于流固耦合的離心風機葉輪動力特性分析[J]. 動力工程學報, 2013, 33(1): 53-60.

[11] 張磊, 郎進花, 王松嶺. 電站軸流風機旋轉失速工況下的葉輪靜力特性研究[J]. 動力工程學報, 2015, 35(5): 387-393.

[12] 羅黎, 王琪, 袁明新, 等. 基于流固耦合的軸流風機結構分析與優化[J]. 江蘇科技大學學報(自然科學版), 2017, 31(1):61-65.

[13] DHOPADE P, NEELY A J, YOUNG J. Fluid-structure interaction of gas turbine blades[C]// Australasian Fluid Mechanics Conference, Auckland, New Zealand, 2010: 477-480.

[14] 毛軍, 楊立國, 郗艷紅. 大型軸流風機葉片的氣動彈性數值分析研究[J]. 機械工程學報, 2009, 45(11): 133-139.

[15] 李春曦, 尹攀, 葉學民, 等. 軸流風機動葉異常對風機內熵產影響的數值模擬[J]. 動力工程學報, 2012, 32(12): 947-953.

[16] 昌澤舟. 軸流式通風機實用技術[M]. 北京： 機械工業出版社, 2005: 43-44.

[17] 李鵬敏, 葉學民, 李春曦. 雙凹槽葉頂軸流風機噪聲預估及葉片靜力結構分析[J]. 電力科學與工程, 2015, 31(3): 7-12.

[18] 張磊, 郎進花, 梁守方, 等. 電站動葉可調式軸流風機葉輪動力特性研究[J]. 中國電機工程學報, 2014, 34(24): 4118-4128