基于GPS定位系統的巡線員所巡電纜確定方法

劉 均， 張 怡， 劉 炯， 陸軼祺， 解 大

(1. 國家電網上海市電力公司 市北供電公司，上海 200072；2. 上海交通大學 電氣工程系，上海 200240)

0 引言

隨著電力系統規模的不斷擴大，人們對其安全性、穩定性、可靠性等方面的要求也在不斷地提高。然而，再精準的保護措施也無法確保電纜的穩定運行，總是會發生監測范圍外的一些人為或自然因素，對電纜產生一定程度的危害，并進一步引發停電等事故。常見的有道路施工誤挖電纜、車輛撞擊、風箏或鳥獸造成短路等[1,2]。為了避免這一類事故的發生，需要定期地對輸配電線路進行巡檢，也就是開展定期的巡線工作。通過巡線往往能提前發現輸配電線路中的隱患，并提前將其解決，降低事故的發生率。因此，在目前的電力系統中，巡線仍舊是不可或缺的一個環節[3,4]。

自20世紀90年代起，GIS地理信息系統逐漸開始在我國的電力領域中嶄露頭角。基于GIS的電力巡檢技術對地理信息的描述是采用一個圖形引擎與對屬性文件進行管理，集合可視化與綜合性于一體，可以很好地整合企業資源和客戶關系的優勢，因此在國外電力行業中已經有了較為廣泛的應用[5]。GIS系統能夠真實反映輸電線路的實際位置走向以及沿線設備的地理位置等各種信息，巡視人員與管理人員通過調用視化系統能夠了解線路狀況，及時處理線路及設備故障。基于GIS的電力巡線系統使得輸電線路信息更直觀形象、有利于管理人員對線路的運行管理[6]。

通過調用巡線員攜帶的智能巡線設備中GPS模塊，便能實時獲取巡線員在工作中所處的具體位置[7]。本文基于定位所得的經緯度坐標及其轉換方式，提出了一種巡線員與電纜位置匹配的算法。首先，通過巡線員的初始位置，將其與預期所巡電纜相匹配。然后對其工作中的位置進行監測，判斷其是否偏離巡線路徑[8]。最后，在巡線完成后依據坐標點列擬合其路徑并計算誤差。通過該算法可以實時監測巡線員工作狀態并準確評估巡線工作的完成程度及巡線員工作情況。

1 巡線員巡線初始位置與電纜的匹配

限制巡線技術發展的一個重要因素就是巡線員具體巡線位置的確定。在提高巡線效率，輔助巡線員工作之前，如何保證巡線員巡檢完畢系統所指定的那條電纜，是所有巡線管理系統所要解決的首要問題。隨著通信行業的迅猛發展，衛星導航技術逐漸成為各國競相發展的重點，而其中最為突出的就是美國GPS系統。該系統對于用戶接收機的精準定位，解決了巡線位置的確定問題。在對巡線圖劃分的增強型網格基礎之上，巡線員在工作時攜帶的智能巡線裝置將會每5～10 s上傳一次巡線員所處位置的經緯度坐標至巡線管理系統[9]。系統將會依據巡線員的前進方向自動將巡線員匹配到最近的一條電纜段上，視為巡線員正在巡檢這一條電纜段。每次巡檢完一條電纜段后，系統還將計算巡線員工作效率等數據，進行后期的分析處理工作。由智能巡線裝置提供的巡線員具體坐標，將先判斷該坐標所處的網格。確定了巡線員所處網格后，便需要進行類似于汽車導航的路徑及電纜段的匹配工作。

Map matching功能是導航中必不可少的一項功能，它不需要定位達到非常高的精確度就能實現用戶接收機位置與當前行駛道路的匹配[10]。這點對于巡線管理系統也是一樣，因為巡線員在巡檢時勢必會沿著一條電纜徑直前進而不會有很大的偏移。巡線員位置判斷與車載導航的區別就是巡線員在沒有巡檢時可能在網格內的任意位置移動。

對巡線員實時位置的具體匹配過程如下：當巡線員要開始巡檢一條電纜段時，由于電纜交匯或分差，系統將會自動為其匹配最近的某條或多條電纜段。巡線員實時位置匹配示意圖如圖1所示。

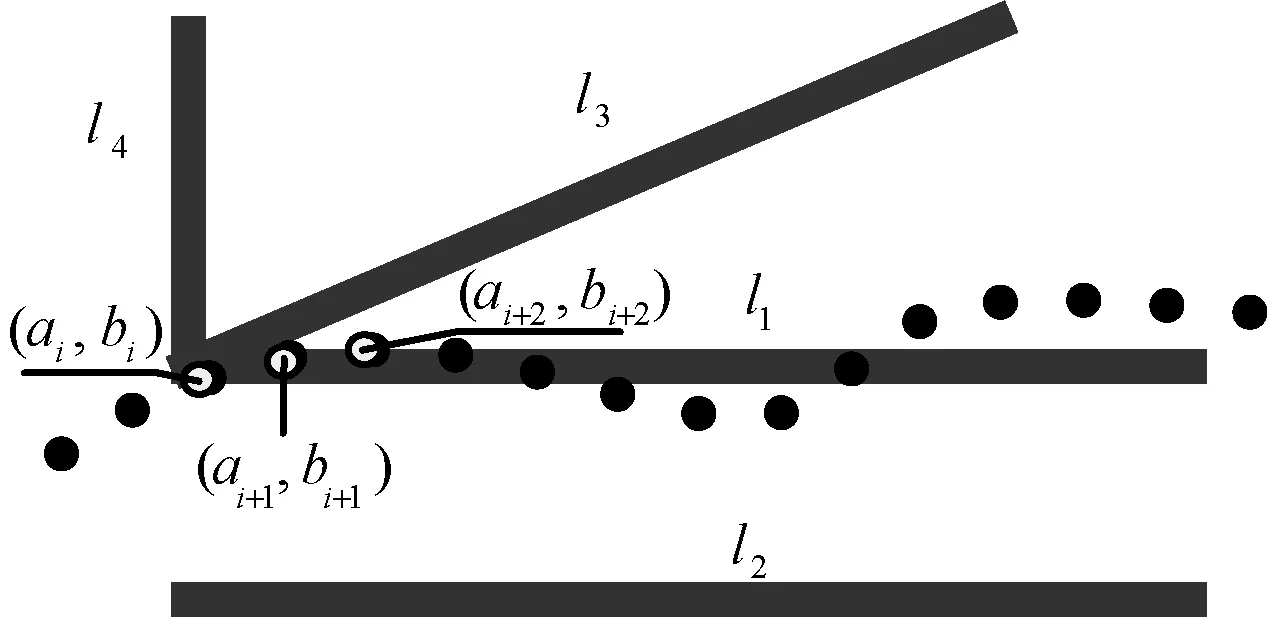
圖1 巡線員與電纜段初始位置匹配示意圖

記lj所在直線方程為b-klja-clj=0，巡線員實時位置的坐標為(ai,bi)，此處的坐標為平面的城市坐標，可與經緯度坐標相互轉換[11]。將網格內所有的電纜段置入備選電纜段集合L，再運用點到直線距離公式計算該初始位置與L內各條可能電纜段的距離dij：

(1)

由此便能選擇可能的電纜段，若其間距離滿足：

0≤dij≤1.5dsup

(2)

式中：dsup為系統認為巡線員在巡查這條電纜段時，其與電纜段之間可能的最大距離。用這些電纜段替換備選電纜段集合L。當L中只有一個元素時，該電纜段即為巡線員所巡查的線段。當L中包含多個元素時，先暫時以與巡線員距離最小的電纜段作為最大可能在巡電纜段。然后等待智能巡線裝置之后5～10 s再次上傳其坐標。

當巡線管理系統獲取新的巡線員GPS坐標(ai+1,bi+1)后，便對L內所有電纜段再次計算巡線員與電纜段的距離：

(3)

同樣進行比較：

0≤di+1,j≤1.5dsup

(4)

在此基礎上還需將第一次的距離計算結果再次納入考慮范圍：

(5)

計算完成后，用符合條件的電纜段再次替換L中的所有元素，若L中元素多于1個，則再次等待巡線員下一次上傳的坐標數據，并重復上述如(ai+1,bi+1)求解過程的步驟，此時的判斷條件變為：

(6)

實際上，對于巡線員所巡電纜段的確定往往不會超過20 s，也即3點的巡線員路徑坐標即可確定巡線員所巡的電纜段。

2 巡線員實時位置與電纜的匹配

巡線員位置與電纜段匹配完成之后，巡線員可能由于各種原因向其他方向運動，這時巡線員可以選擇通過智能巡線裝置暫停巡線工作，那么巡線管理系統則會將其工作時間暫停，并停止對其的監控，直至巡線員再度手動開啟巡線工作。若巡線員并沒有選擇暫停，巡線管理系統則能判斷出該巡線員終止了對該條電纜段的巡線工作。

巡線管理系統在巡線員巡查某一電纜段的任意時刻，均會利用式(1)計算巡線員所處位置與其所巡電纜段的垂直距離，如圖2所示，一旦該距離超出了允許范圍，也即：

dij≥dsup

(7)

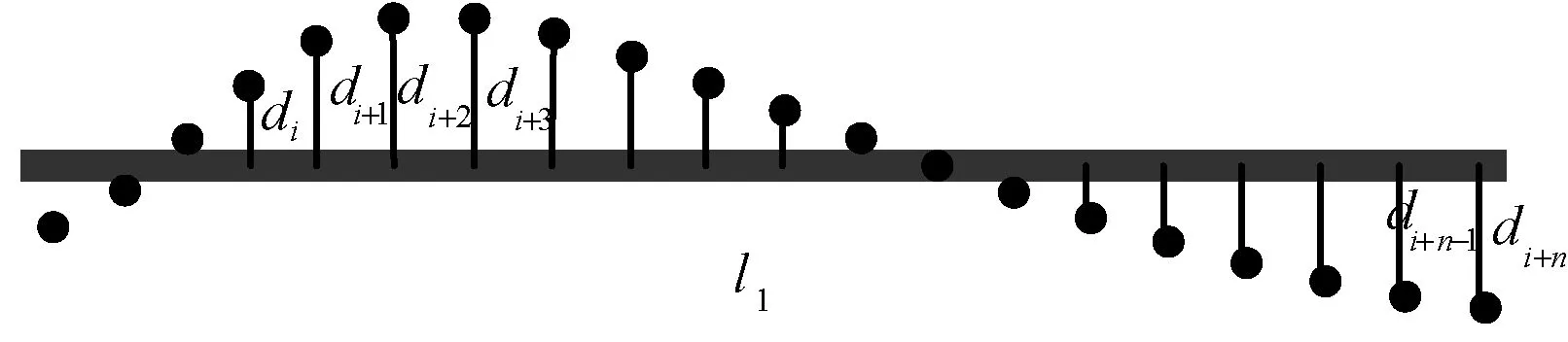
圖2 巡線員與電纜段實時位置匹配示意圖

則系統判定巡線員不再繼續巡查該電纜段。當巡線員完成一條電纜段的巡檢任務后，他便能通過智能巡檢裝置上傳該電纜段的巡檢信息，并通過巡線管理系統統一分析管理。

巡線員實時位置與電纜段的匹配工作是一種對于巡線員工作實時的數據處理方式，除此以外，巡線員上傳的數據均將存儲于數據庫中。同時，巡線員在巡檢每一條電纜段(l1)時，所上傳的經緯度坐標(a1,b1),(a2,b2),(a3,b3)，…，(an,bn)均會保存于該電纜段的集合L1中，而該集合則包含于網格集合G中。

3 巡線路徑擬合及誤差分析

巡線員巡線路徑的擬合以及誤差分析均是基于最小二乘法的原理實現的。在工程技術和科學實驗中，常常得到兩個有函數關系觀測量的一系列有序對，如何根據這些有序對來確定它們的函數曲線，這就是實驗數據處理中的曲線擬合問題。為了解決這一類問題，最小二乘法應運而生，其基本思想是：給定一組實驗數據，這些數據往往是有序數對，根據誤差平方和最小化原則，找出這些數據的最佳函數匹配[12]。在利用最小二乘法實現曲線擬合時，雖然能夠很好地擬合有序對，但是需要進行大量復雜的計算，而且得到的擬合函數往往是高次的，這進一步增加了復雜性。

將最小二乘法運用在巡線員的坐標位置變化上，便能大致擬合出巡線員所選擇的巡線路徑。在確保誤差很小的前提下，為了有效利用巡線圖增強型網格的特點，對于巡線員的最短路徑擬合采取分段線性擬合的方式。巡線員每巡檢一條電纜段，便視為一條擬合路徑。因此，可以將該分段線性擬合的方式分為電纜段路徑及非電纜段路徑2類。

3.1 電纜段路徑擬合

對于某一條選定的電纜段(l1)，從其集合L1中調出其中的所有巡線員坐標元素(a1,b1),(a2,b2),(a3,b3)…(an,bn)，對其的線性擬合將以電纜段l1所在直線方程b-kl1a-cl1=0為參照。設待求擬合直線為：

b-kl1a-cl1+Δcm=0

(8)

由于巡線員在巡檢某電纜段時，其位置與該電纜段的相對位置偏差不會很大，因此直線方程(8)中唯一的待求量Δcm也會很小。使用最小二乘法的原理，選定一個足夠小的循環步長ε，以及范圍(mmin,mmax)內的整數循環步數m。這樣一來，所要求的變量就成為了循環步數m。據此，便可以將擬合直線方程改寫為：

b-kl1a-cl1+mε=0

(9)

計算(a1,b1),(a2,b2),(a3,b3)，…，(an,bn)與其的距離平方均根，也即為巡線員路徑相對于電纜段的誤差值，根據式(1)可求得每點與電纜段的距離d11,d21,d31，…，dn1，并據此求得誤差值：

(10)

對范圍(mmin,mmax)內的整數m進行遍歷，計算其Em的值，然后比較這些Em，其中最小的那個值對應的m0即為所要求的參數。

(11)

將其回代入式(9)，便能得到通過最小二乘法所求得的電纜段路徑擬合直線：

b-kl1a-cl1+m0ε=0

(12)

m的上限mmax和下限mmin分別是直線l1兩側距離其最遠的兩坐標點決定，若這兩條直線分別為：

b-kl1a-cl1+Δcm1=0

(13)

以及：

b-kl1a-cl1+Δcm2=0

(14)

則易得mmax與mmin分別為：

(15)

(16)

巡線員在巡線時經過絕大多數均為電纜段路徑，因此采取的近似電纜段所在直線的線性擬合算法將大大節省普通最小二乘法的計算復雜度，而其誤差也并不會有太大的增加，這是巡線圖增強型網格的一大優勢。

3.2 非電纜段路徑擬合

網格中的電纜段并不一定是全部鄰接的，如圖3所示的巡線員實時位置坐標集合、系統擬合路徑以及電纜段之間將產生部分誤差，巡線員也將勢必在某兩條電纜段的端點間自由移動。巡線員在這些位置移動時的坐標將被記錄在L的補集CUL中，對于選定的某兩條電纜段間的自由移動區域，不是一般性地同樣以(a1,b1),(a2,b2),(a3,b3)，…，(an,bn)來表示它們，通過一般的最小二乘法來擬合非電纜段路徑。

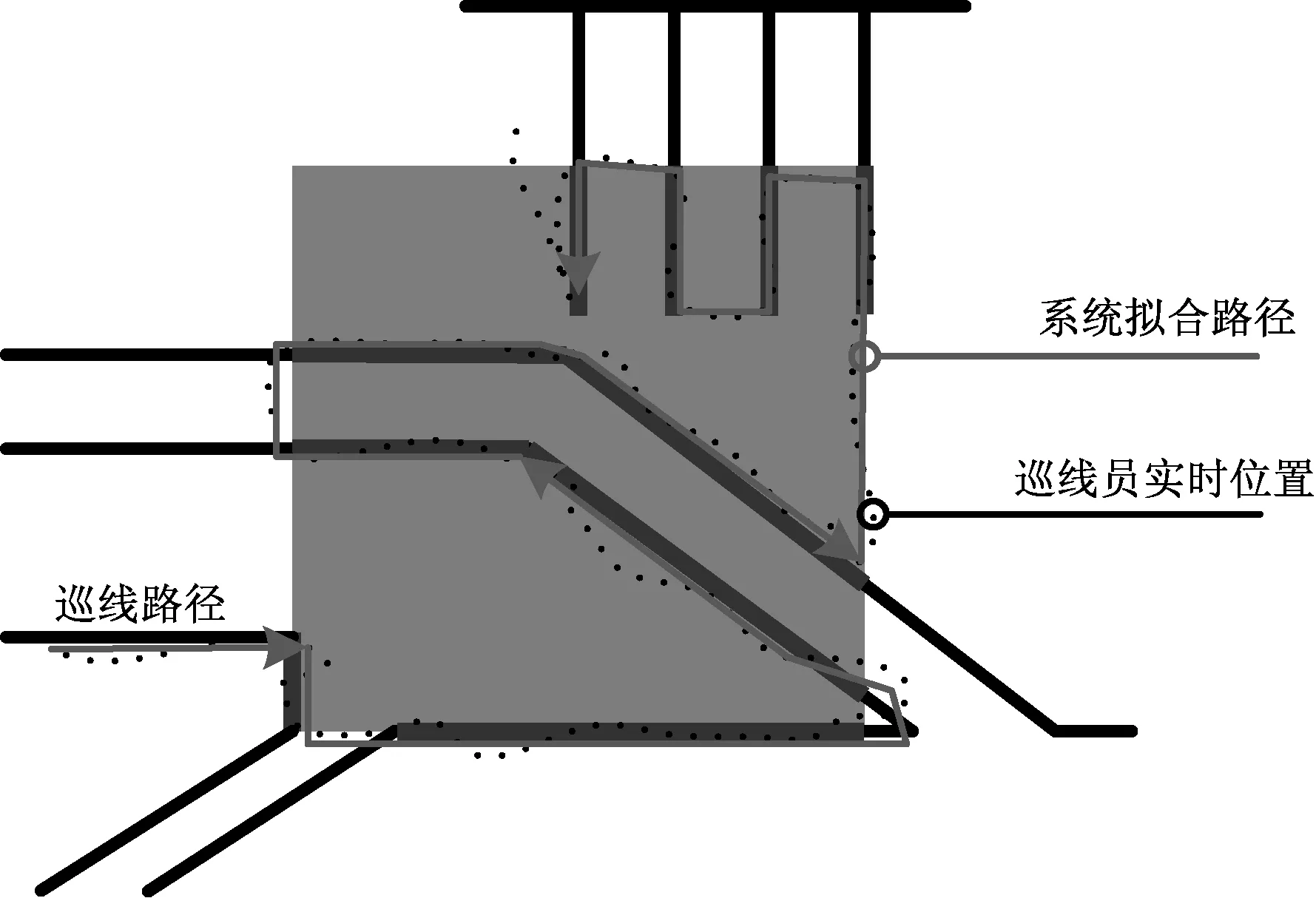
圖3 模擬巡線路徑擬合圖

設所求擬合直線方程為

b-ka-c=0

(17)

待估參數為k及c，令

k=k0+Δk

(18)

c=c0+Δc

(19)

式中：k0及c0為k及c的初始值，一般選為巡線員之前或之后巡查電纜段的k及c值。

據此，便可以得到誤差方程為：

(20)

將所有n個點的坐標代入，便能得到向量:

(21)

依據最小二乘法判別準則：

VTV=min

(22)

對應于VTV的最小值，便能得到所要求的k值及c值。

非電纜段路徑在巡線管理系統中處于相對次要的地位，因為實際上只需要記錄巡線員不在巡線時所消耗的時間即可。

3.3 誤差分析

誤差分析同樣是針對巡線員在巡檢電纜段時的路徑而言的，對于某一選定的電纜段l1而言，巡線員所經過的坐標點為(a1,b1),(a2,b2),(a3,b3)，…，(an,bn)，則定義其巡線過程中的絕對誤差為：

(23)

其相對誤差為：

(24)

不難發現，e*的求解公式與式(10)相似。此類相對誤差的提出是為了避免由于巡線員在不同電纜段巡線所花時間不同而造成的絕對誤差差距。此相對誤差在計算巡線效率及權重時有很重要的作用。

巡線員所攜帶的智能巡線裝置也存在著定位精度的問題，因此在巡線員所處位置與電纜段匹配后的巡線過程中，系統認為巡線員在巡查這條電纜段時，其與電纜段之間可能的最大距離dsup一般定為5～10米，也即緯度經度相差0.1 s左右的距離偏差。

4 算例分析

為了檢測巡線員與電纜匹配算法的實際效果，上海市市北塊區域的電纜被選為試點區域，并安排進行實地測試。由于電纜段十分復雜，所以展示測試的一部分結果如圖4所示，圖中的黑點即為實驗時所獲取的巡線坐標點。巡線員攜帶著帶有GPS定位功能的巡線設備正常工作，后臺軟件便能獲取其實時坐標并記錄下來與事先完成的電纜段擬合線段相比較，執行匹配算法，便能成功實現路徑的匹配以及擬合。可以看出，在電纜段本身長度較短的情況下，由于獲取坐標點的數量很少，因此對路徑的匹配可能出現偏差。但由于其本身路徑就短，所以實際效果并沒有出現很大的誤差。

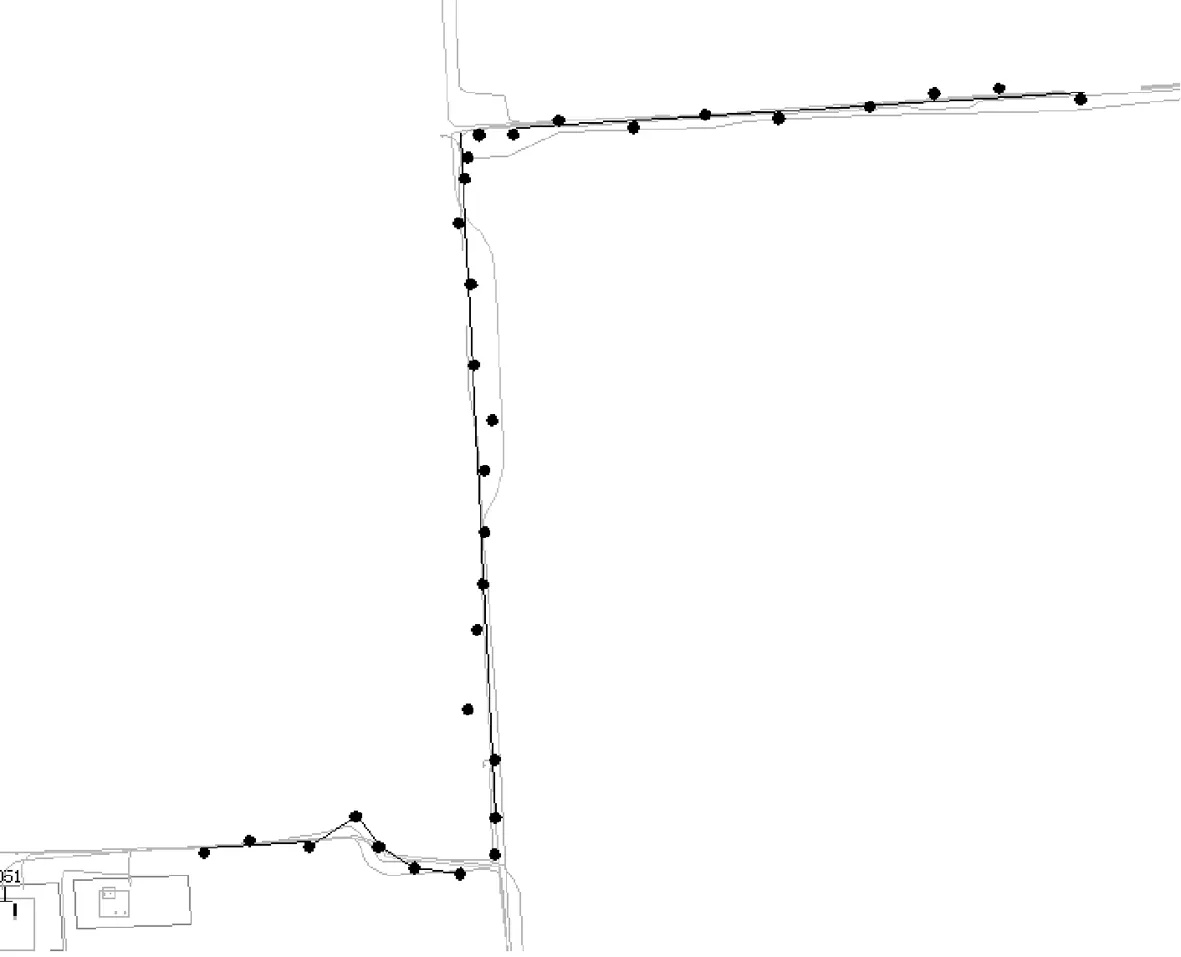
圖4 模擬巡線路徑擬合圖

試驗區域的某條路徑取點情況如表1所示，該段路徑自己電纜段近似直線方程為0.051 814x-y+338.988 65=0，而實際擬合直線方程為0.074 2x-y+493.494 7=0，兩者在相同的區間[-6 925.289 6,-6 854.837 9]內偏差距離最大處僅1.05365。由于巡線員的配合，坐標偏差均質只有0.842。

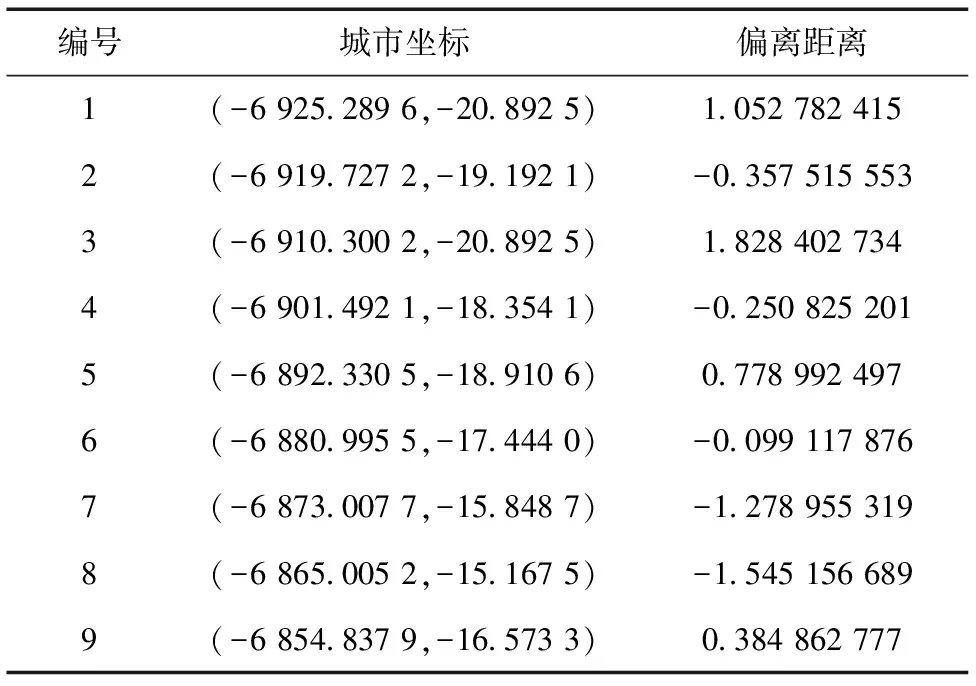
表1 單條路徑數據表

在這次測試中，結果符合預期，主要的誤差并不來源于路徑匹配及擬合算法，而是來自電纜段向直線的近似。

5 結論

(1)提出了巡線員坐標散點與電纜段路徑的匹配算法，能夠有效地確定巡線工作時巡線員所巡路徑，當電纜段路徑較短時可根據需求手動改變坐標獲取速率或允許偏差，實現具體目標。

(2)通過匹配算法得出屬于同一路徑的點列，并依據最小二乘法實現對于巡線路徑的擬合及誤差分析，從而為巡線工作的考核提供數據參照。

(3)具體巡線工作實踐中，能夠實現需求，與巡線管理軟件及智能巡線設備契合度高，總體完成度也較高。

參考文獻：

[1] 胡毅, 劉凱, 吳田,等. 輸電線路運行安全影響因素分析及防治措施[J]. 高電壓技術, 2014, 40(11):3491-3499.

[2] 蔡澤祥, 王星華, 任曉娜. 復雜網絡理論及其在電力系統中的應用研究綜述[J]. 電網技術, 2012, 36(11):114-121.

[3] 許金凱, 張立中, 金珈成,等. 高寒區機載電力巡線光電穩定吊艙系統設計及應用[J]. 中國電機工程學報, 2012, 32(31):200-208.

[4] 王鵬, 劉鋒, 梅生偉,等. 高壓輸電線巡線機器人控制體系構建及動作控制器設計[J]. 清華大學學報(自然科學版), 2011，51(7):921-927.

[5] 閭國年, 袁林旺, 俞肇元. GIS技術發展與社會化的困境與挑戰[J]. 地球信息科學學報, 2013, 15(4):483-490.

[6] 宋小冬, 鈕心毅. 城市規劃中GIS應用歷程與趨勢——中美差異及展望[J]. 城市規劃, 2010,34 (10):23-29.

[7] 田雪竹, 初永良, 范永存,等. 基于農村電網的GPS巡線系統管理軟件的設計[J]. 東北農業大學學報, 2009, 40(2):111-113.

[8] 韓小濤, 張哲. 基于智能手持機的高壓巡線管理系統開發[J]. 電力自動化設備, 2003, 23(4):47-48.

[9] 陳得民, 張元. 基于網格劃分的傳感器網絡定位方法的研究[J]. 計算機應用研究, 2009, 26(5):1685-1686.

[10] TONG X H, CHUN W U, QING W U, et al. A novel vehicle navigation map matching algorithm based on fuzzy logic and its application[J]. Journal of Central South University of Technology, 2005, 12(2):214-219.

[11] 謝鳴宇, 姚宜斌. 三維空間與二維空間七參數轉換參數求解新方法[J]. 大地測量與地球動力學, 2008, 28(2):104-109.

[12] 田垅, 劉宗田. 最小二乘法分段直線擬合[J]. 計算機科學, 2012, 39(s1):482-484.