PMSM帶前饋控制的模型參考自適應矢量控制系統的研究

周 陽， 馬立新， 袁滄虎

(上海理工大學 光電信息與計算機工程學院，上海 200093)

0 引言

因永磁同步電機(Permanent Magnet Synchronous Motor, PMSM)擁有價格低廉、速度調節的范圍寬以及動態響應快等優勢，應用前景很廣。在傳統的磁極定向控制系統中，PMSM的精確控制基本依賴于準確的轉子速度以及轉子位置的測量，然而安裝位置傳感器，如光電編碼器和旋轉變壓器，會使控制系統成本、體積增加，在某些場合受限，如溫度較高的場所，限制了PMSM的應用推廣[1～2]。無位置傳感器控制為解決該問題提出了很好的方法。PMSM的無位置傳感器技術無需安裝位置傳感器，利用檢測到的電機繞組中的有關電信號，以及再利用一定的控制算法，從而對轉速以及轉子位置進行計算。

因此，越來越多的研究人員開始專注于無位置傳感器控制系統的研究。目前已有許多控制方法可以對電機的轉速進行估計，主要有基于基波數學模型的三相永磁同步電機無傳感器控制和基于高頻信號注入的三相永磁同步電機無傳感器控制這兩大類。其中基于基波數學模型的三相PMSM五傳感器控制技術依賴三相PMSM基波激勵數學模型中與轉速有關的量(如產生的反電動勢)進行轉子位置和速度估算，由于電動機在零速和極低速時，有用的信噪比很低，通常難以提取。從根本上說，對基波激勵的依賴性最終導致了相關方法在零速和極低速運行時對轉子位置和速度的檢測失效。因此，基于基波數學模型的三相PMSM無傳感器控制技術主要應用于中高速場合，常用的控制算法有：滑模觀測器算法(SMO)、模型參考自適應算法(MRAS)、擴展卡爾曼濾波算法(EKF)等[3，4]。

本文首先闡述了PMSM帶有前饋控制的模型參考自適應矢量控制系統的原理，再設計合理的自適應律來對電機參數進行識別，再結合電壓前饋解耦的控制方法，然后采用MATLAB建立系統的仿真模型，以此來驗證該方法[5]。

1 算法原理

1.1 模型參考自適應算法原理

MRAS算法是一種自適應控制系統的算法。從結構上分MRAS算法可以分為可調模型、參考模型和自適應律3部分。MRAS的基本理論是：期望模型選取為不包含待定系數的表達式，可調節的模型選取為包含待定系數的表達式，此外，兩個模型輸出量要有一樣的物理含義，然后再利用它們輸出量的差值，利用選定適宜的自適應律對PMSM未知系數進行識別[6]。

1.1.1 參考模型與可調模型的確定

對于表貼式三相PMSM，同步旋轉坐標系下的電壓方程表達式[7～9]：

(1)

為了獲得可調模型，對上式作變換，可得：

(2)

定義

(3)

則式(2)變為

(4)

再將(4)改寫為狀態空間形式：

(5)

其中：

從公式(5)可以得出，狀態矩陣A中包含了轉子轉速，因此可以將該式當作可調模型，ωe為有待確定的可調系數，而三相PMSM的本體就選作參考模型。

1.1.2 參考自適應律的確定

將上式(4)用估計值形式來表示，可得[10]：

(6)

可簡寫為：

(7)

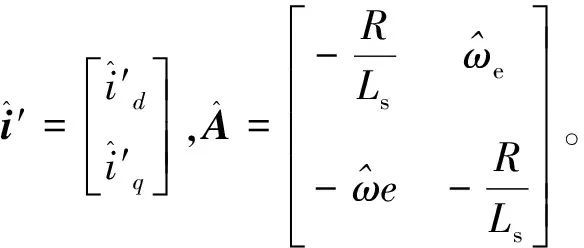
(8)

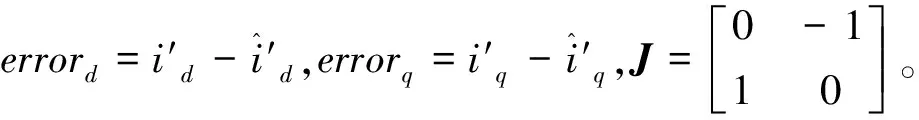
將公式(8)簡寫成以下形式：

(9)

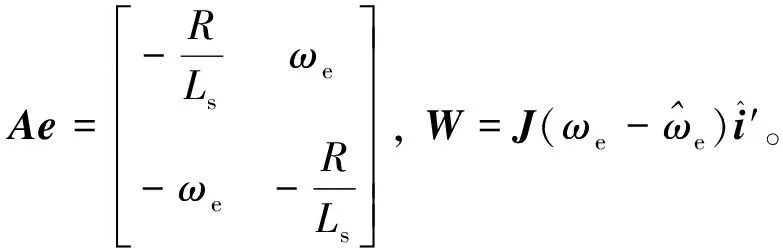
根據Popov超穩定理論，若想要讓該控制系統處于穩定狀態，得滿足以下2個要求[11]：

1)傳遞矩陣H(s)=(sI-Ae)-1為嚴格正定矩陣；

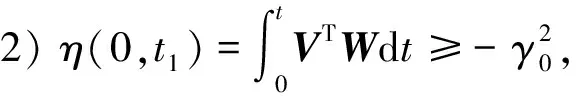
對Popov不等式進行反向計算可得所需的自適應律，且結果：

(10)

將式(10)改寫為如下表達式：

(11)

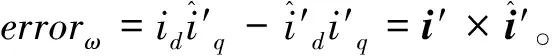
將公式(3)代入公式(10)，可得：

(12)

對公式(11)求積分，便可求得所需的轉子的位置估算值：

(13)

MRAS的實現框圖如圖1所示。

圖1 MRAS的實現框圖

1.2 電壓前饋控制

由公式(1)定子電流id、iq分別在q軸和d軸方向產生交叉耦合電動勢。

若id、iq完全解耦，式(1)變為[12～15]：

(14)

式中：ud0和uq0分別為電流解耦后的d軸和q軸電壓。

將式(14)拉普拉斯變換后，可得

Y(s)=G(s)U(s)

(15)

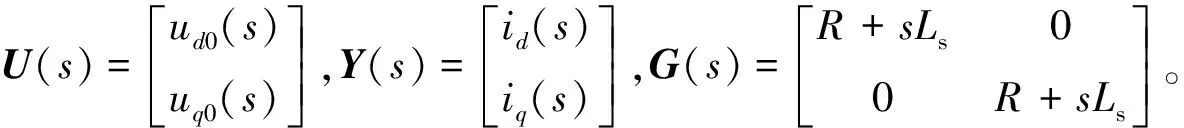
利用常規的PI控制器并結合電壓前饋解耦控制方法，可得到d-q軸電壓分量為：

(16)

式中：Kpd和Kpq為PI調節器比例增益，Kid和Kiq為PI調節器積分增益。

電壓前饋解耦單元的電流環PI控制器的系統結構框圖，如圖2所示。

圖2 前饋解耦單元系統結構方框圖

2 MATLAB仿真驗證及結果分析

根據圖1所示的MRAS實現框圖，采用MATLAB/SIMULINK構建系統仿真模型。MRAS的MATLAB仿真模型如圖3所示。帶有前饋解耦控制單元的MRAS三相PMSM無傳感器矢量控制系統結構框圖，如圖4所示。

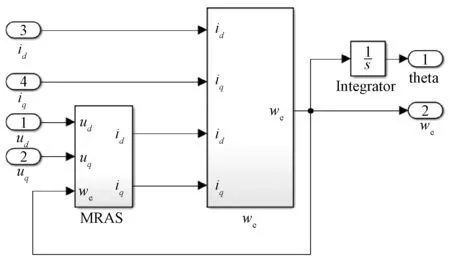
圖3 MRAS仿真模型

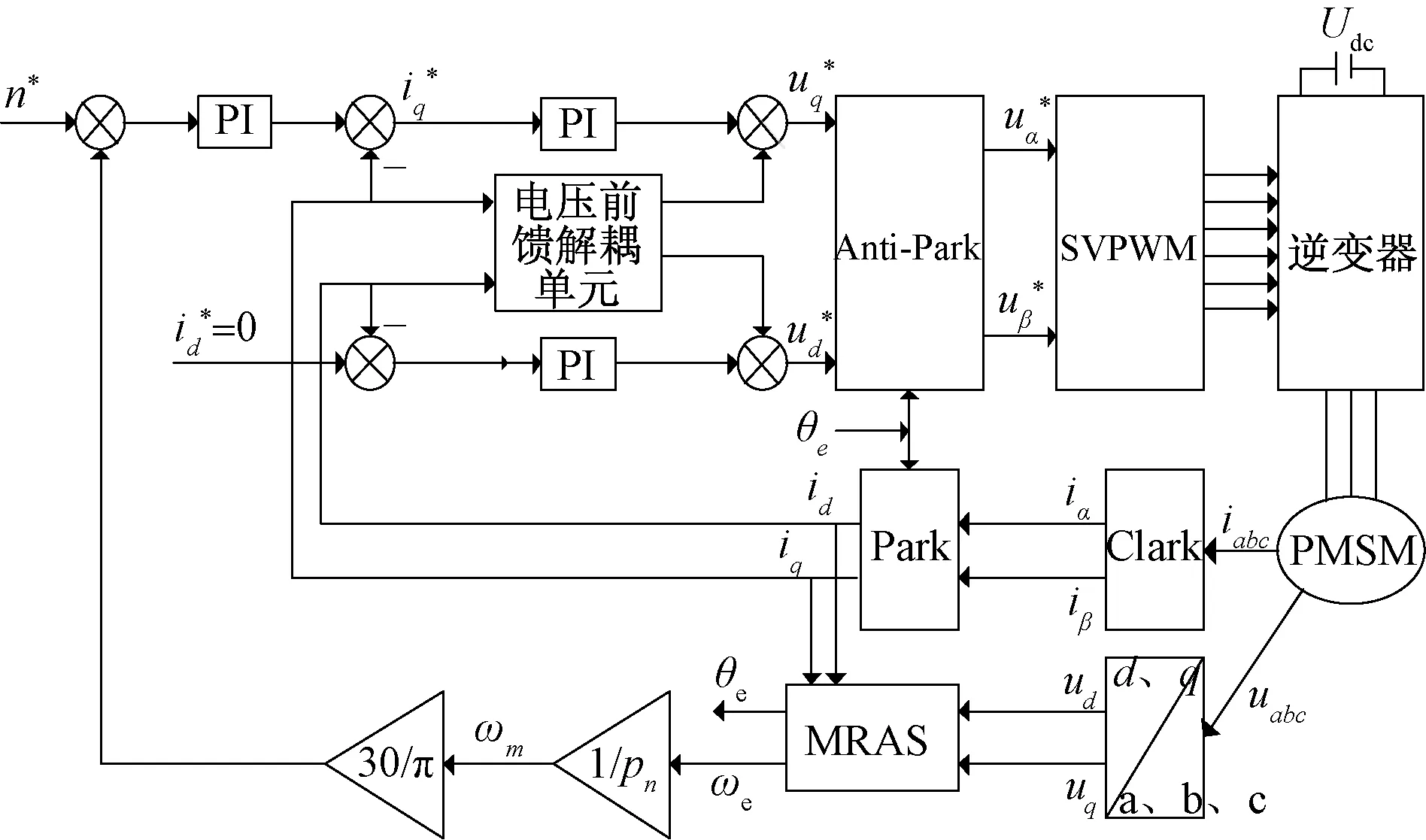
圖4 帶有前饋控制的MRAS的三相PMSM 矢量控制系統結構框圖

根據圖4的帶有前饋解耦控制單元的MRAS三相PMSM無傳感器控制結構框圖，搭建MATLAB/SIMULINK仿真模型。其中，PWM周期為0.000 1 s。仿真中電機參數為：極對數Pn=4，定子電感Ls=8.5 mH,定子電阻R=2.875 Ω，磁鏈Flux=0.175 Wb，轉動慣量J=4.8×10-6kg·m2。

傳統控制系統中PI電流控制器分別對d軸和q軸的電流實行閉環控制，但是這種方法忽視了它們之間的相互耦合影響，降低了控制系統的動靜態特性，所以本文又設計了結合常規PI調節器與電壓前饋解耦單元的方法，以此來改善系統的動靜態特性。

給定轉速設置為600 r/min，空載和負載條件下的MATLAB仿真結果及分析如下所示：圖5～圖8為空載運行，圖9和圖10為運行在0.1 s時的加負載10 N·m。

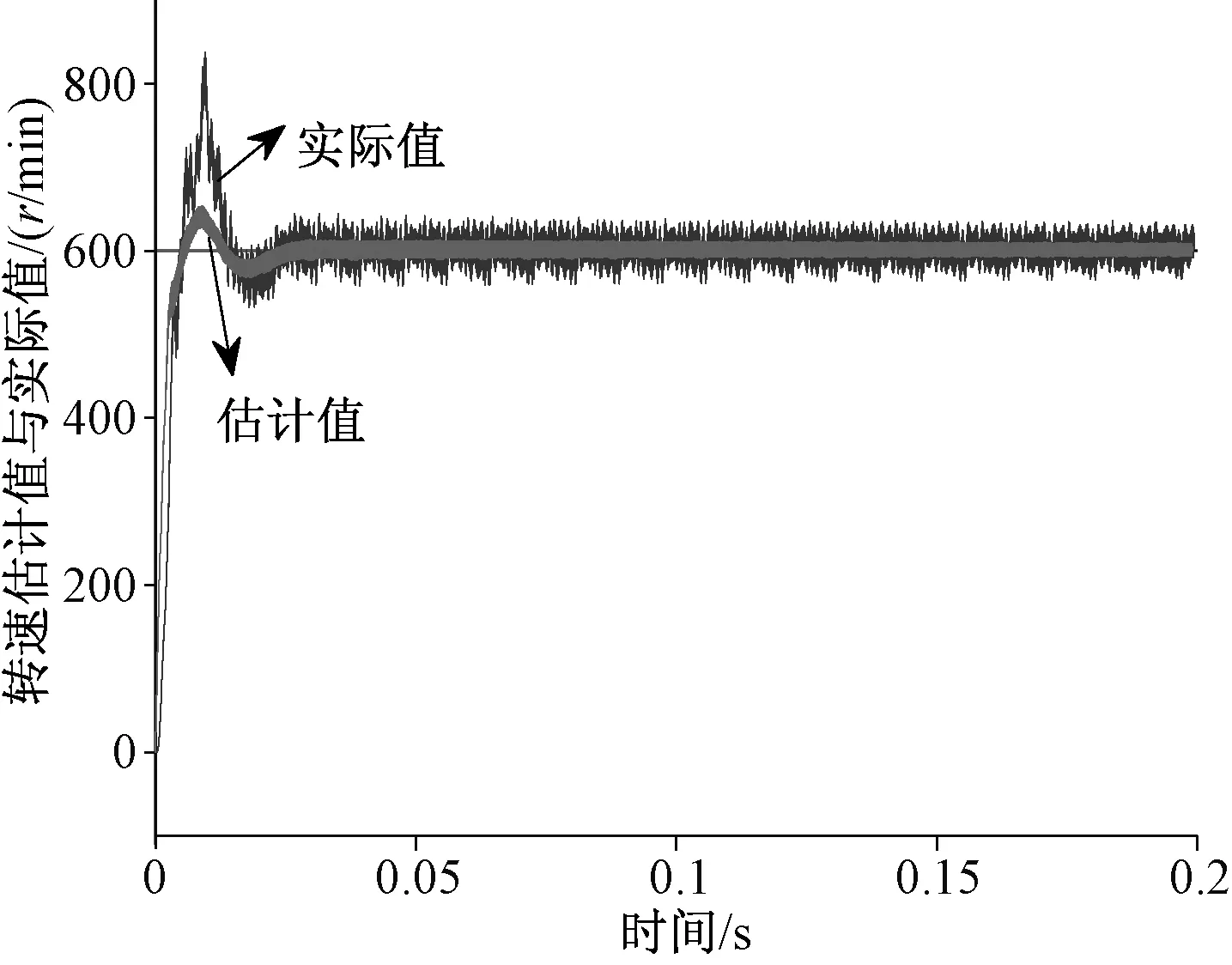
圖5 轉速估計值與實際值

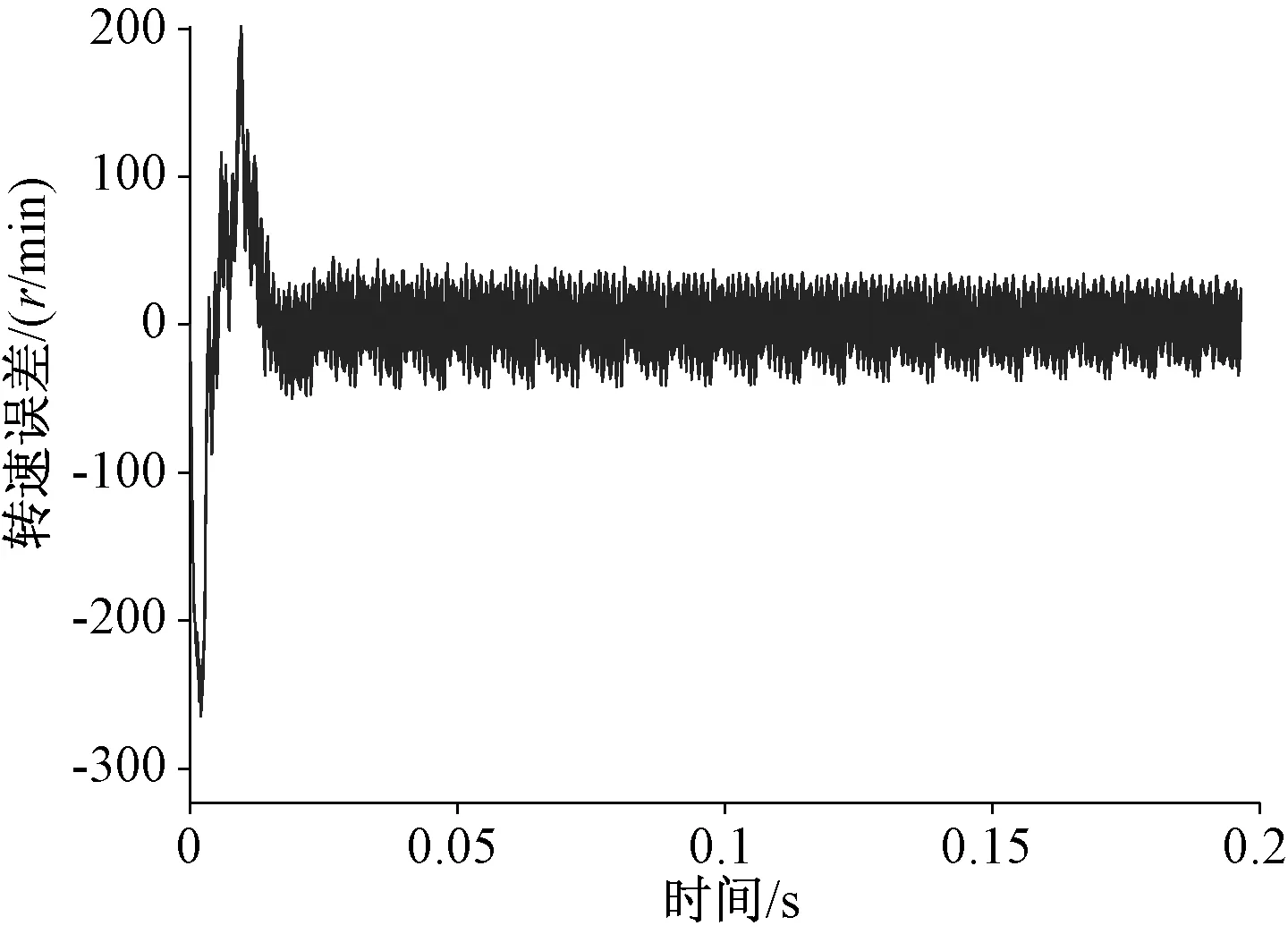
圖6 轉速誤差

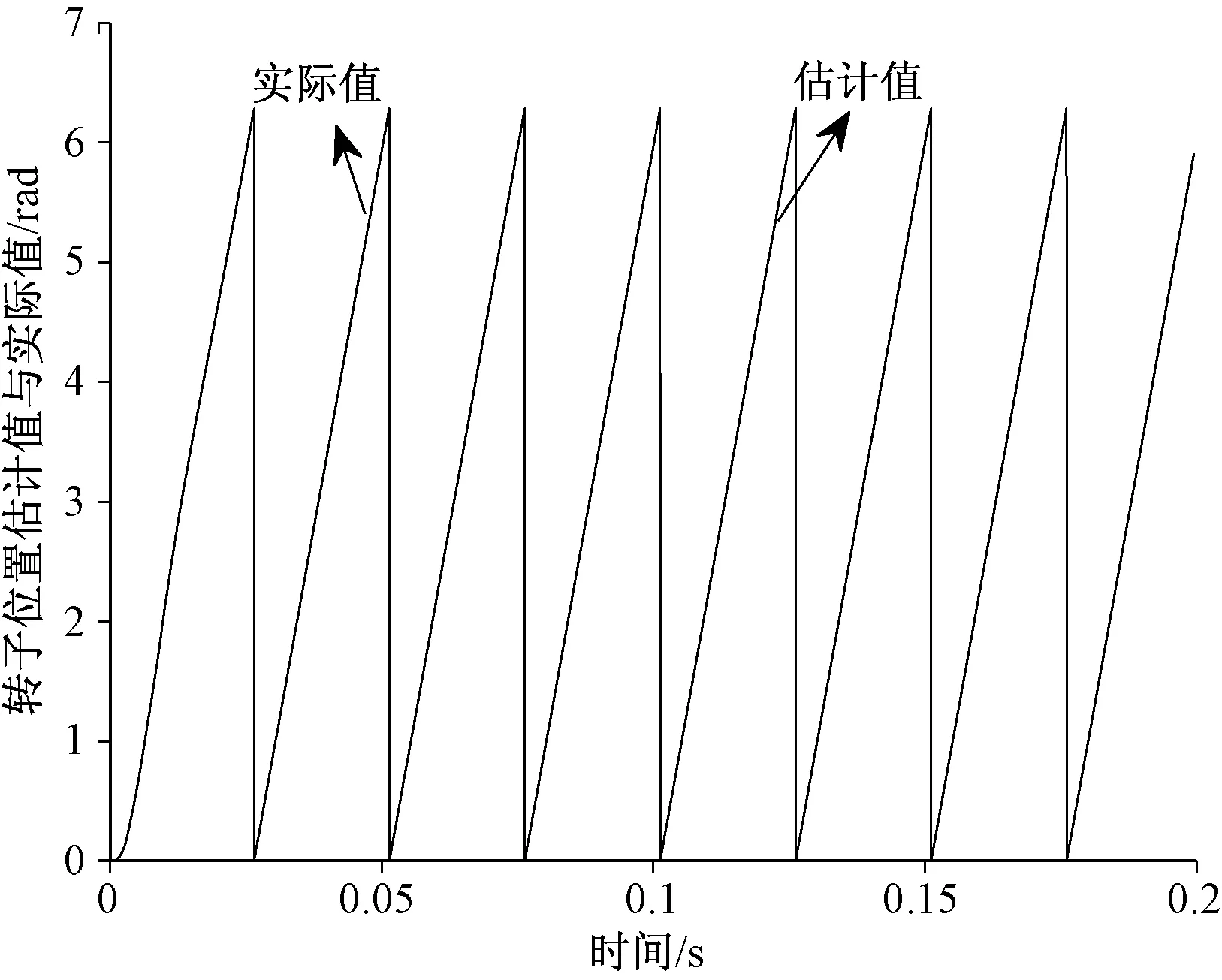
圖7 轉子位置的估算值與實測值

圖5為PMSM轉速估算值與實測值的變化曲線，圖6為PMSM轉速估算誤差變化曲線。從圖中可以看出，電機速度從零速上升到參考轉速600 r/min過程中，轉速估計值的變化趨勢與轉速實際值變化趨勢基本一致。在電機轉速上升階段，轉速的估算誤差較大，但當轉速上升到參考值并穩定運行后，轉速估算誤差開始漸漸減小，直至保持穩定。

圖7為PMSM轉子位置估算值與實測值的變化曲線，圖8為PMSM轉子位置估算誤差的變化曲線。從仿真的結果圖可以看出，電機轉子的位置估算值一直緊隨轉子的位置實際測量值，在電機速度上升階段，電機轉子位置估計誤差較大，在 -0.26 rad到0.02 rad之間，隨著電機轉速上升且穩定運行后，轉子位置的估算誤差逐漸減小，接近于零，且保持穩定。

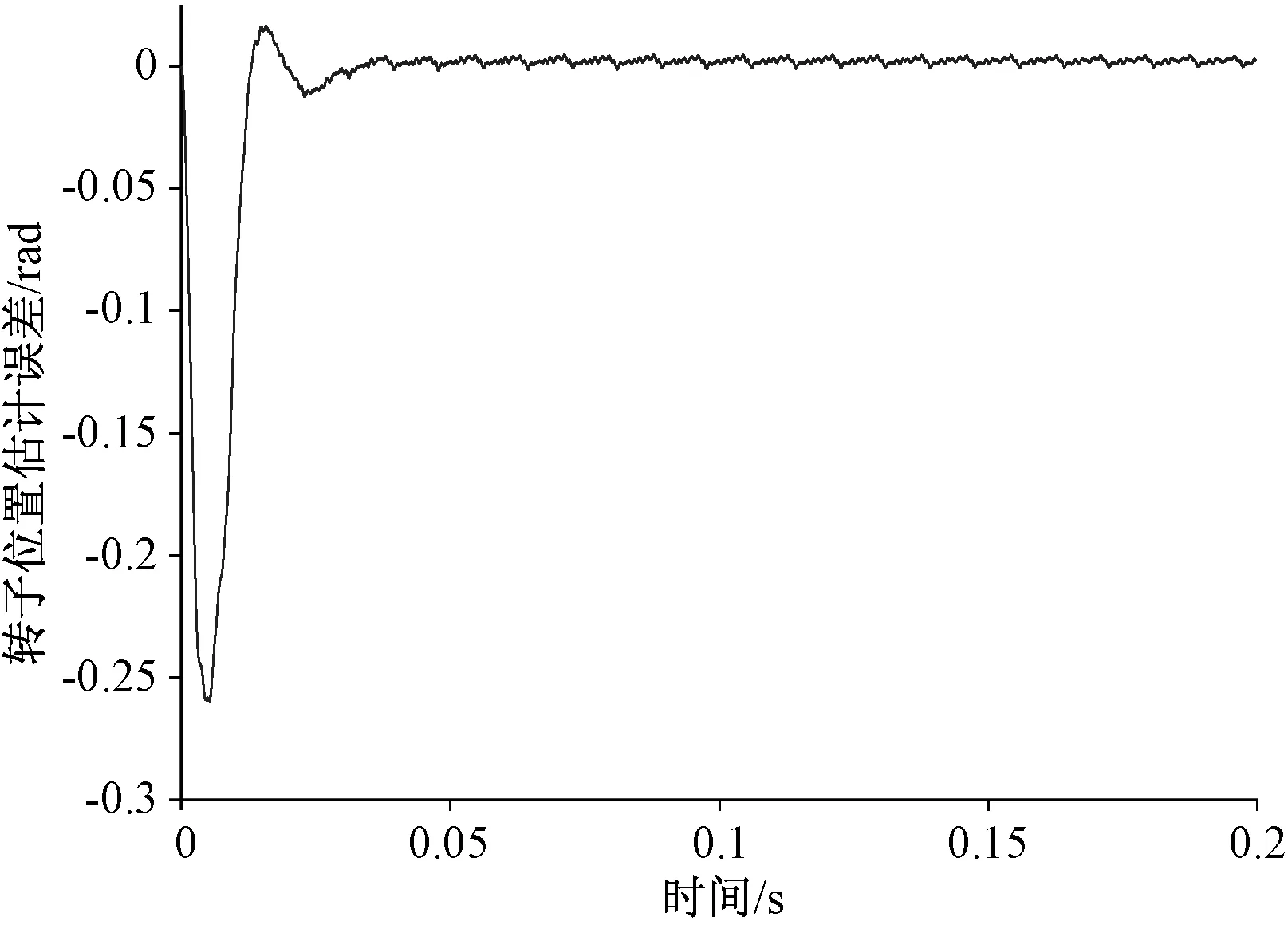
圖8 轉子位置估計誤差

圖9為負載條件下PMSM轉速估算誤差變化曲線。圖10為負載條件下PMSM轉子位置估算誤差的變化曲線。從仿真結果可以看出，在剛加負載時，轉速估算誤差和電機轉子位置估計誤差都有一些波動，但是系統調節較快，兩個誤差都逐漸減小，直至保持穩定。

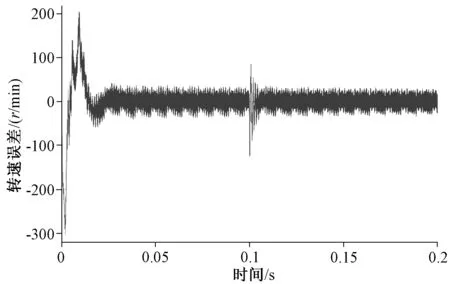
圖9 轉速誤差(負載)

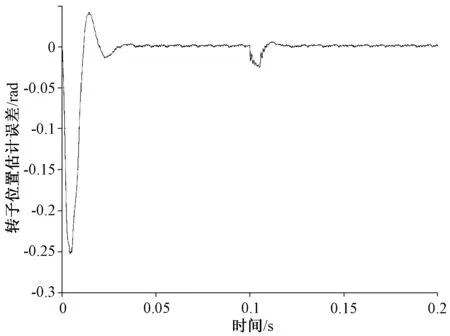
圖10 轉子位置估計誤差(負載)

從以上的仿真結果可以表明，帶有前饋解耦控制單元的MRAS無傳感器的矢量控制技術能夠滿足實際電機控制性能的要求。

3 結論

由原理推導及仿真結果分析可知，本文提出的把MRAS和前饋解耦控制單元結合起來，應用于PMSM矢量控制系統中，再通過設計適宜的自適應律來對電機的未知參數進行識別，獲得有關的轉子位置和速度是可行的。通過電壓前饋解耦控制單元，并利用交直軸電流調節器對其進行補償，達到d-q軸電流的解耦的目的，并以此改善控制系統的動靜態特性。經過仿真模型的驗證，也最終證實了本文所提出的方法的轉子位置及轉速的計算精度高，系統穩定性好，響應快，能夠滿足實際電機控制的需求，可以替代光電編碼器。

參考文獻：

[1] 王鑫，李偉力，程樹康.永磁同步電動機發展展望[J].微電機，2007，40(5)：69-72.

[2] LIANG YAN，LI YONGDONG. Sensorless control of PM synchronous motors based on MRAS method and initial position estimation[J]. Electrical Machine sand Systems,2003,(1)：96-9.

[3] 敬華兵，廖力清.基于模型參考自適應方法的無速度傳感器永磁同步電機控制.機車電傳動[J]，2007，4(1)：33-36.

[4] 尚喆，趙榮祥，竇汝振.基于自適應滑模觀測器的永磁同步電機無位置傳感器控制研究[J].中國電機工程學報，2007,22(4)：17-23.

[5] 齊放，鄧智泉，仇志堅，等. 基于 MRAS 的永磁同步電機無速度傳感器[J].電工技術學報，2007(22)：53-57.

[6] 李崇堅. 交流同步電機調速系統 [M]. 北京：科學出版社,2013.

[7] 李永東，張猛，肖曦，等．永磁同步電機模型參考自適應無速度傳感器控制方法[J]. 電氣傳動, 2004,34: 302-306.

[8] 王子輝,陸凱元,葉云岳.基于改進的脈沖電壓注入永磁同步電機轉子初始位置檢測方法[J].中國電機工程學報,2011,31(36):95-101.

[9] 李冉.永磁同步電機無位置傳感器運行控制技術研究[D].杭州:浙江大學, 2012.

[10] 谷善茂,何鳳有,譚國俊,等.永磁同步電動機無傳感器控制技術現狀與發展[J].電工技術學報,2009,24(11):14-20.

[11] 馬立新,范洪成,黃陽龍.永磁伺服電機模糊PID自整定SVPWM控制研究[J].電子測量技術,2016,39(6):20-23.

[12] 王飛宇,田井呈,卓克瓊，等.基于改進模型參考自適應算法的永磁同步電機轉動慣量辨識[J].電機與控制應用,2016,43(8):63-67.

[13] 樊英杰, 張開如, 馬慧,等. 基于模糊PI永磁同步電機優化矢量控制系統的研究[J]. 電氣傳動, 2016, 46(3):15-19.

[14] 卞延慶, 莊海, 張穎杰. 基于模糊PI的永磁同步電機矢量控制研究[J]. 微電機, 2015, 48(11):62-66.

[15] 張洪帥, 王平, 韓邦成. 基于模糊PI模型參考自適應的高速永磁同步電機轉子位置檢測[J]. 中國電機工程學報, 2014, 34(12):1889-1896.