基于Delta調節器的微網逆變器控制策略研究
朱 輝, 黃瀟瀟, 楊海興
(1. 國網天津市電力公司 城西供電分公司,天津 300113; 2. 國網天津市電力公司 電力科學研究院,天津 300384; 3. 河北省送變電有限公司,河北 石家莊 050000)
0 引言
隨著功率半導體器件開關速度和額定容量的提高,在光伏發電、電動汽車充電和和分布式儲能裝置等領域,電壓源型逆變器受到了越來越多的關注[1~3]。傳統的控制負載輸出電流或者輸出功率的方法是利用晶閘管可控整流器和開關頻率恒定的逆變器實現這一過程的。但是整流器中的開關器件通常工作在硬開關狀態,進一步增加了功率損耗以及設備的體積和重量[4]。
電壓源型串聯諧振逆變器工作在零電流開關狀態,逆變器控制方法包括閉環控制、無差拍控制和重復控制等。單閉環電壓控制方法雖然控制結構簡單易于實現,但是動態響應性能差[5]。電壓和電流雙閉環控制盡管動態響應特性快,但是控制參數設定取值復雜[6]。而無差拍控制與重復控制雖然控制誤差值低,但依賴于復雜數學模型的建立[7,8]。綜上所述,提出了一種應用于串聯諧振逆變器的電流可調Delta調節器CRDM(Current Regulated Delta Modulator),控制脈沖序列的產生,這種方法采用高增益的bang-bang調節器,因而具有較強的魯棒性和響應速率[9]。但是CRDM控制輸出電流常伴隨有非零穩態誤差和偏置,導致輸出功率性能惡化。本文通過對工作在零電流開關狀態下的串聯諧振逆變器進行動態電流模型分析[10],提出一種改進的帶有積分復位功能的CRDM調節器,通過引入積分復位環節,減小直流側電流偏置,提高電網側功率因數,通過仿真分析和實驗驗證了提出的控制策略。
1 零電流開關串聯諧振逆變器動態電流模型
為了對電流可調Delta調節器進行簡化并進行有效地分析,首先提出了一個基于串聯諧振逆變器的離散時間動態模型,其原理如圖1所示,其中負載電路由等效電抗Leq、電阻Req和電容Cc串聯連接。
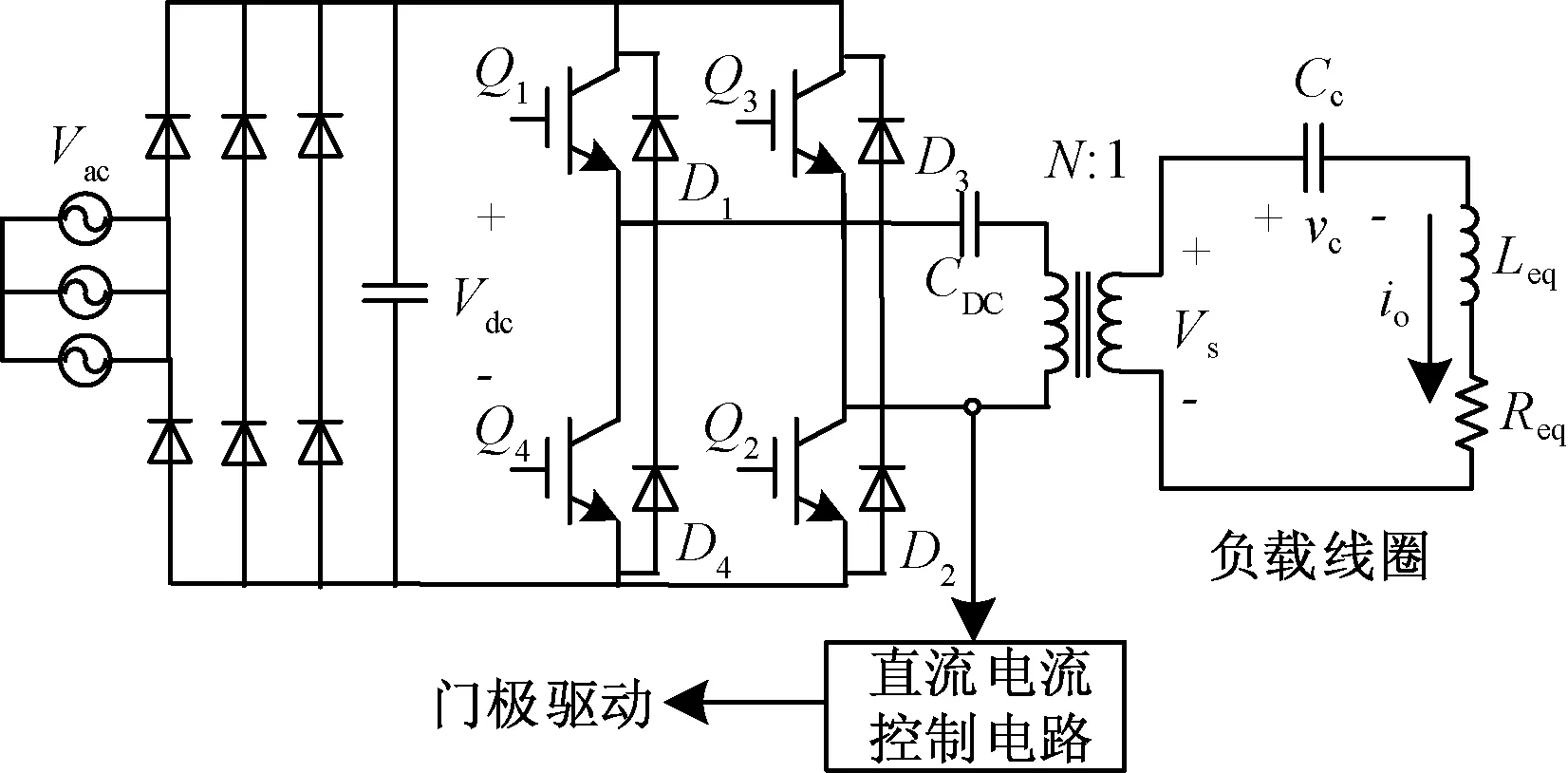
圖1 串聯諧振電路原理圖
已知匹配變壓器二次側輸出電壓初始值為Vs,對應時刻t=0,輸出電流io。槽路電容電壓vc的簡化表達式可以表示為公式(1)和(2):
(1)
(2)
式中:α為衰減系數;Q為品質因數;ωr為固定角頻率;ωd為時域角頻率;φ為相位。
式中:vc為等效負載電容電壓;Vs為輸出電壓初始值;io為輸出電流;Leq為等效電抗;Req為等效電阻;Cc為等效電容。
由于每一個功率開關器件總是在電流過零點時刻改變其開關狀態,因而開關器件的開關頻率總是等于負載諧振頻率。串聯諧振電路輸入端電壓值由逆變器開關狀態決定,如公式(3)所示。
(3)
式中:Vdc為輸入端電壓值。
定義一個離散變量M(k)來描述逆變器的運行模式,如公式(4)所示,
(4)
結合公式(3)和(4)可以寫成:
vs(t)=VdcM(k)sign(io(t)),
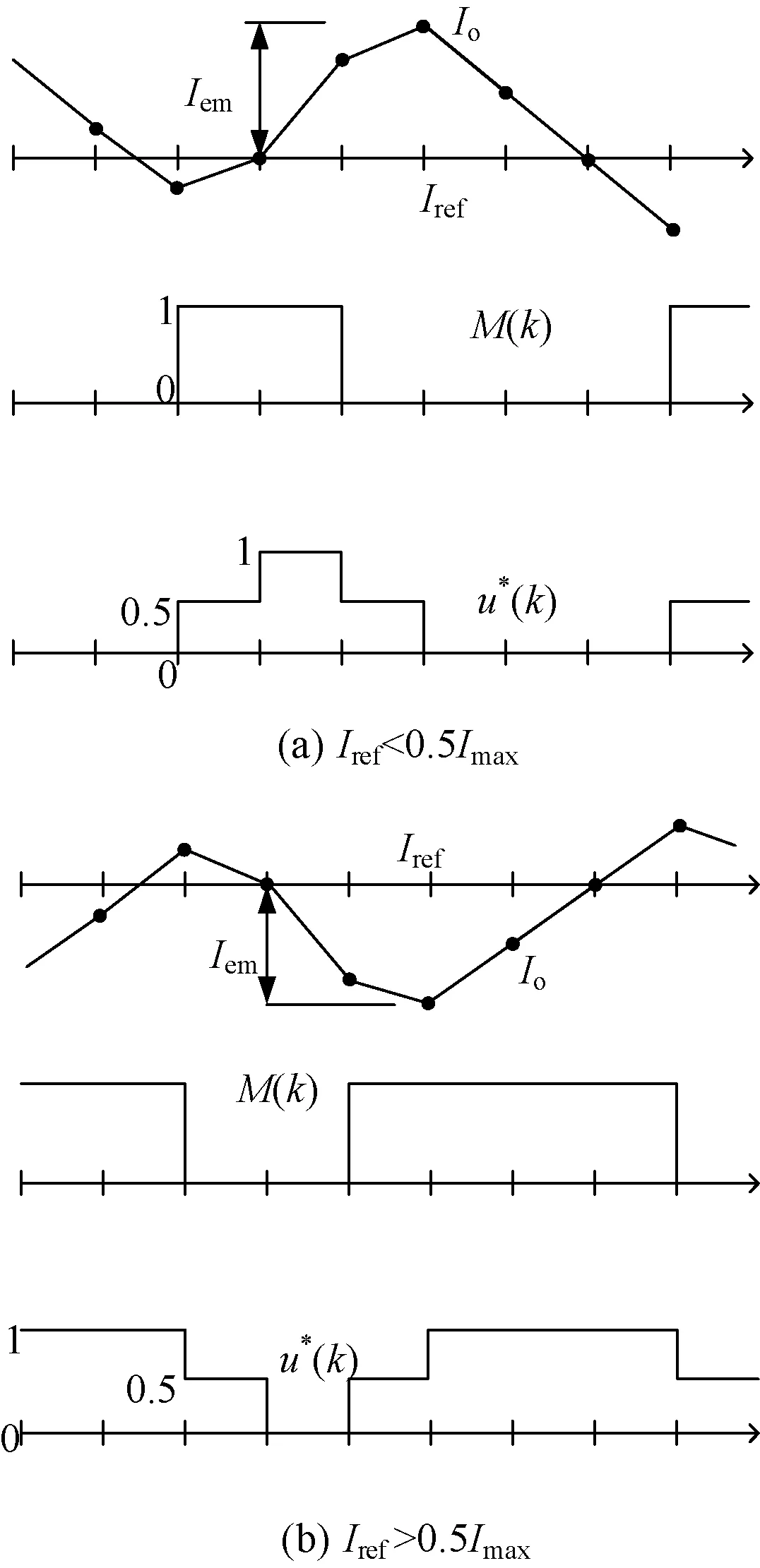
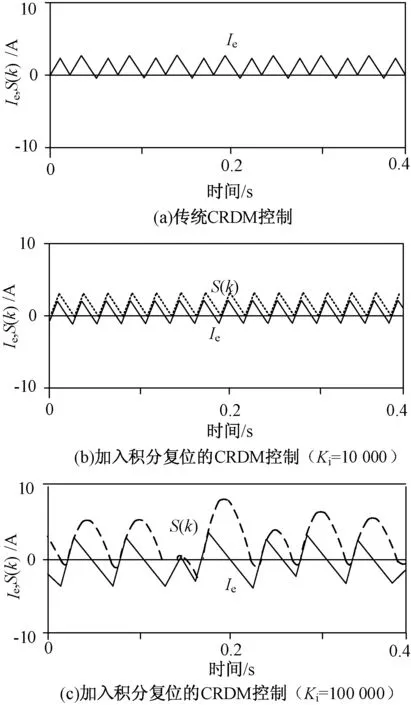
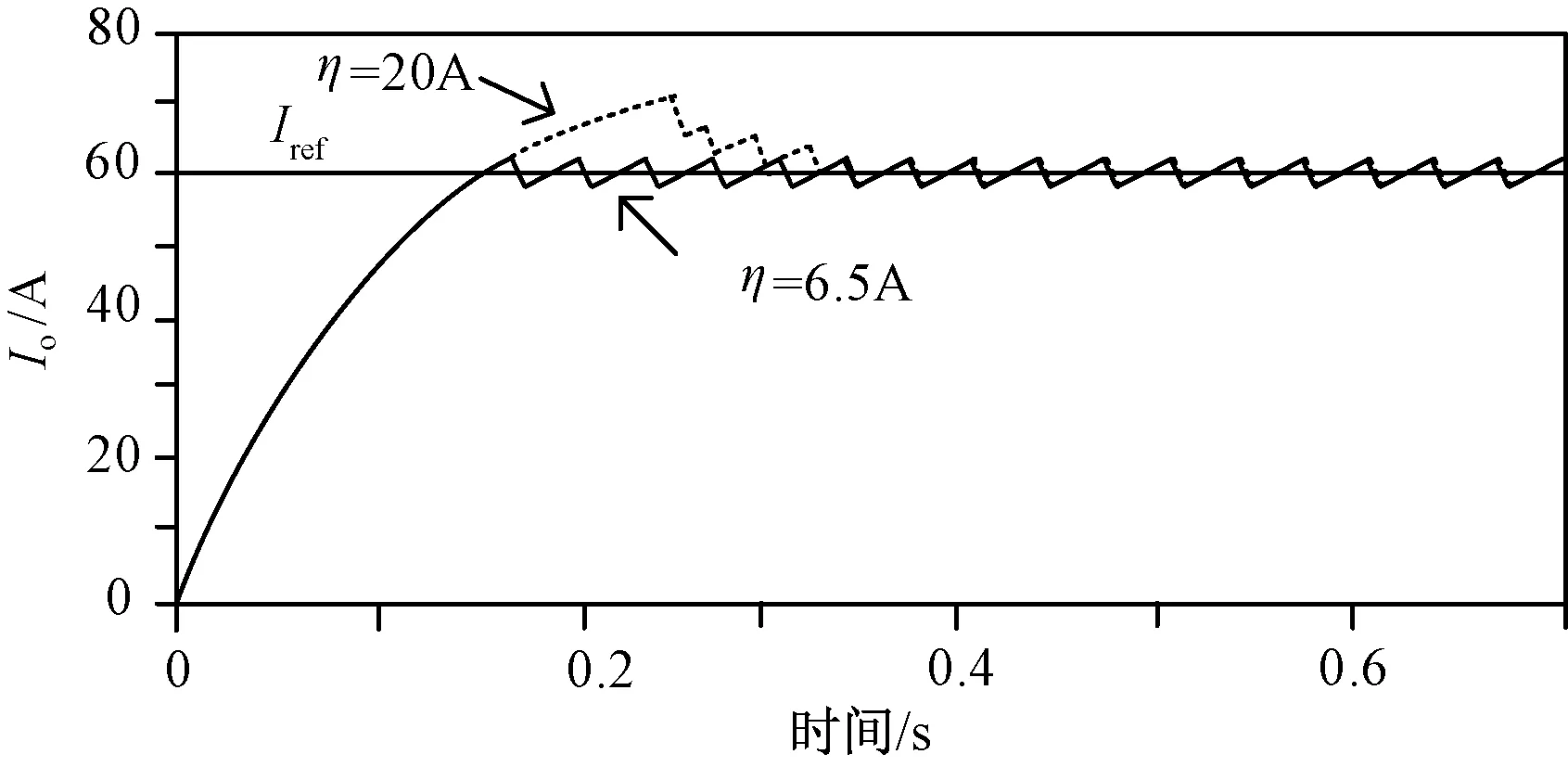
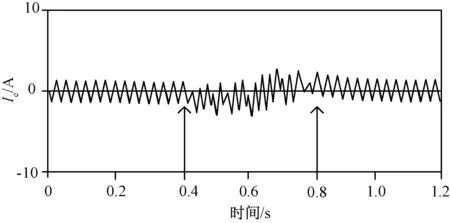
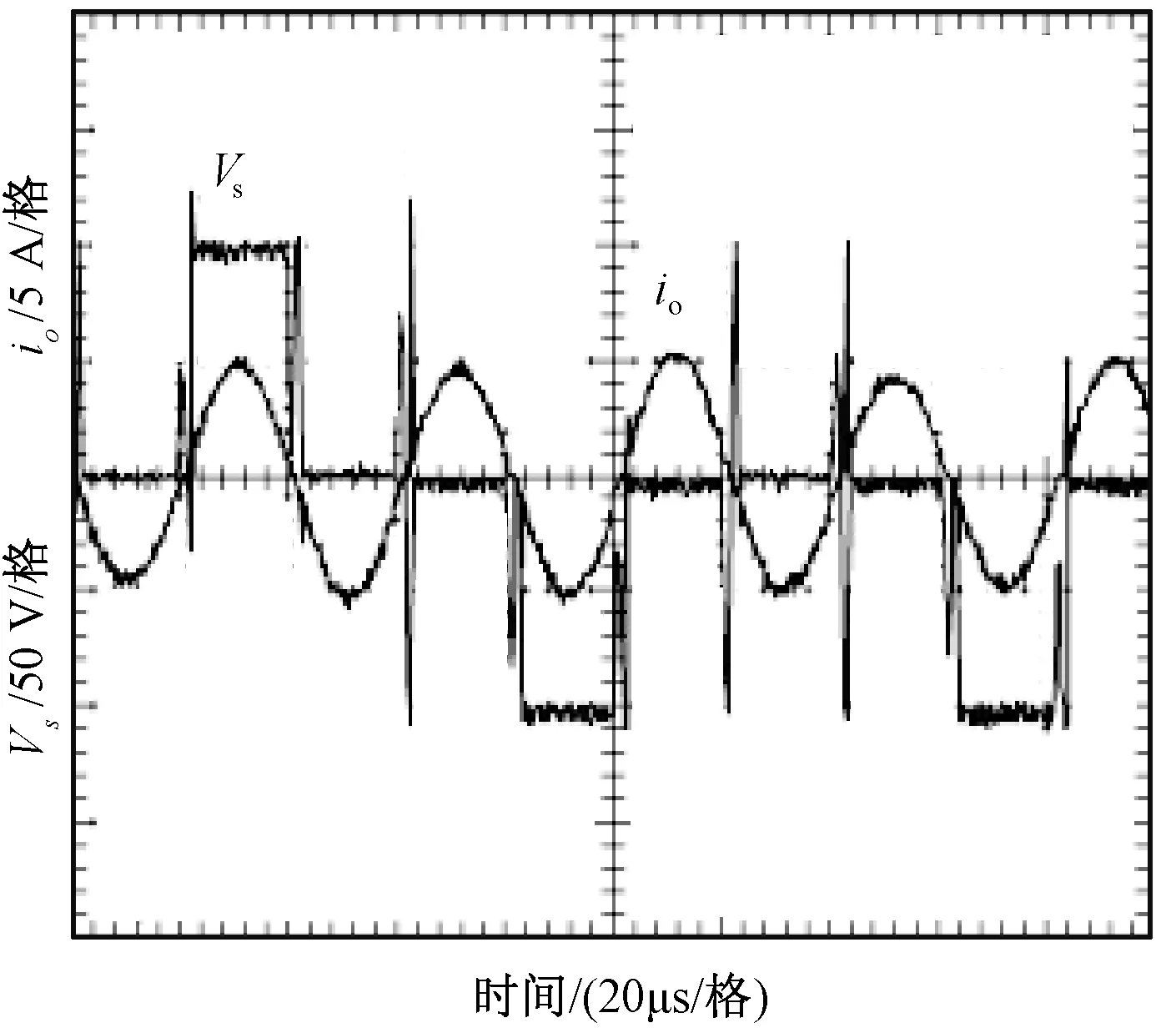
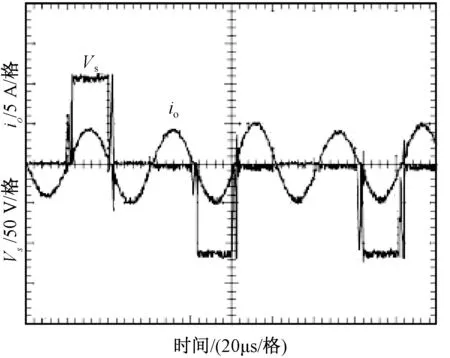
kT (5) 式中:T=π/ωd,代表半個諧振周期;sign(io(t))為輸出電流符號函數。 由式(1)(2)和(5)可得: (6) Vc(k+1)=|vc(kT+T)|= (7) 式中:Io(k)為負載輸出電流狀態量;Vc(k)為電容電壓狀態量;負載品質因數Q?1,ωd≈ωr,φ≈0。 將公式(7)代入(6),可以得出離散時間下的電流Io(k+1): Io(k+1)=ΦIo(k)+Γu*(k+1) (8) 式中:Io(k)為輸出電流離散狀態量;u*(k)為等效控制輸入量;Φ和Γ為調節系數。 (9) (10) (11) 式(11)的等效控制輸入u*(k+1)取值范圍為{1,0.5,0,-0.5,-1},則流過負載線圈的輸出電流最大值可以由式(8)(9)和(10)得出: (12) 式中:Imax為輸出電流最大值。 在一個采樣周期內,負載電流的變化決定了電流紋波的幅值,關系表達式為: (13) 式中:ΔI(k)為電流紋波幅值狀態量。 對于階躍輸入指令,電流控制器的瞬時響應速率快,超調量小。由式(8)可知,零電流開關串聯諧振逆變器工作在常規采樣系統下,圖2(a)顯示了電流可調Delta調節器的控制原理圖。由式(13)可知,在這種情況下,控制輸入值只有0和1兩個狀態,輸出狀態切換速度或者電流變化速率不能被恰當地調整,導致直流側電流紋波含量高,電流偏置大。因此,為了減小偏置值,在傳統的CRDM調節器的前饋通道上加入了一個積分器,控制原理如圖2(b)所示。 圖2 電流可調Delta調節器(CRDM) 變結構控制理論常被用于分析具有開關性質的系統[11,12]。基于滑模變結構控制的開關狀態可以表示為: S(k)=Ie(k)+Kiz(k) (14) 式中:S(k)為滑模變結構控制開關狀態量;Ie(k)為誤差電流狀態量;Ki為積分器增益;z(k)為積分增益系數。 z(k+1)=z(k)+TIe(k) (15) 對應的M(k+1)的值為: (16) 為了滿足滑模變結構控制要求,需要滿足以下條件: S(k){S(k+1)-S(k)}<0 (17) 則平均誤差的動態特性可以由S(k)=0這一時刻對應的誤差值決定如下: Ie(k)=e-KiTIe(0) (18) 由式(18)可知,適當增大積分增益Ki可以更好地減小直流偏置。為了進一步擴大Ki的上限值,當直流側電流誤差值大于預設的誤差帶寬η時,積分器被強迫復位,控制原理如圖3。每半個諧振周期內,采集逆變電路直流側電流值Io,與參考電流值Iref進行比較,產生誤差信號Ie。PI控制器的輸出信號經過bang-bang調節器的調節決定下一時刻逆變器的運行模式[13]。借助這種控制方法,通過合理地設計積分器增益Ki和誤差帶寬η,可以有效地減少直流電流偏置,避免較大超調量的產生,同時也可以保證負載輸出電流的連續性。 圖3 加入積分復位的電流可調Delta調節器控制原理圖 首先,確定積分增益Ki的最大值,考慮式(14)中的積分增益系數z(k),當z(k)=1時,直流側電流誤差的幅值Ie(k)等于S(k)。為了滿足式(17)滑模控制的要求,可以聯立式(8)(14)和(15),得出S(k): S(k+1)-S(k)=(1-Φ)Io(k)-Γu*(k+1)+ KiTIe(k)=-ΔI(k+1)+KiTIe(k) (19) 當S(k+1)-S(k)=0,解得Ki: (20) 式中:Iref為電流參考值。 當控制輸入信號M(k+1)=1時,u*(k+1)可能的取值為{1,0.5}。當u*(k+1)=1時,Ki滿足: 0 (21) 式中:K1為在u*(k+1)=1且Ie(k)>0時對應的Ki值。 當控制輸入信號M(k+1)=0時,u*(k+1)可能的取值為{0,0.5}。當u*(k+1)=0時,Ki滿足: 0 (22) 式中:Ko為在u*(k+1)=0且Ie(k)<0時式(20)對應的Ki值。 當u*(k+1)=0或1時,由式(21)(22)可得Ki滿足: (23) 但是,當u*(k+1)=0.5時,Ki無法解出,此時對應S(k)<0,Io(k)<0.5或者S(k)>0,Io(k)>0.5兩種情況,為了減少這種情況下的電流紋波,下一時刻S(k+2)的值應滿足: S(k){S(k+2)-S(k+1)}<0 (24) 此時,u*(k+2)的可能取值為{1,0},并同時滿足M(k+2)=M(k+1)。借助上述式(23),當滿足Iref=Imax或者Iref=0時,可以得出: (25) 然后確定誤差帶寬η的最小值。為了減小超調量,需要選取一個較小的η值,同時滿足在穩態情況下最大電流誤差值不使積分器復位。圖4(a)顯示了當Iref<0.5Imax情況下誤差帶寬η值,圖4(b)顯示了當Iref>0.5Imax情況下誤差帶寬η值,再結合式(23)(24)和(25),得出誤差帶寬η最小值為: ηmin=max{|ΔI(u*=0.5)|+|ΔI(u*=1)|, (26) 圖4 不同Iref下對應的電流誤差和控制輸入值 為了驗證提出的電流可調Delta調節器的控制性能,使用一個額定功率5 kW、工作頻率100 kHz的逆變器系統,主要參數為:Vdc=120 V,Req=0.5 Ω,Leq=20.0 μH,Cc=0.12 μF,N=3,Q=26,Imax=72 A。 圖5顯示了當參考電流值為60 A時的電流誤差Ie穩態響應波形。其中圖5(a)對應的是在傳統CRDM控制下的穩態電流誤差波形,誤差值基本維持在2 A左右,對應誤差率為3.3%。圖5(b)中加入了復位積分器,穩態偏置進一步減小,由式(25)中計算可得積分增益最大值為 12 000。當Ki值過大會導致直流側電流紋波含量增加,波形對應圖5(c),其中Ki=100 000。 圖5 直流側電流穩態誤差仿真波形 圖6中的(a)(b)兩條曲線分別表達了不同誤差帶寬值對應的階躍輸入信號下的輸出電流Io響應波形,其中積分增益Ki=10 000。由圖6可知,當誤差η=6.5 A,滿足最小誤差帶寬時,直流側電流響應超調量幾乎為零;而當η=20 A時,超調量較大。 圖6 當參考電流值Iref=60 A階躍響應波形 圖7顯示了當0.4 ms時,負載由Req=0.5 Ω到0.25 Ω變化和當0.8 ms時,負載由Req=0.25 Ω到0.5 Ω變化控制器的輸出響應波形。在此過程中,本文提出的電流控制器表現出了較強的電流調節性能,誤差值維持在允許的范圍內。 圖7 當t=0.4 ms和0.8 ms時負載變化時電流波形 為了驗證上述理論分析與仿真過程,設計了一臺單相逆變器實驗樣機,其主要參數為:額定功率25 kW,額定輸出電壓200 V,開關頻率為22 kHz;主電路開關器件選用IGBT雙管結構;積分增益Ki= 10 000,誤差帶寬η=8.2 A。 圖8為加入積分復位器前的Delta調制諧振逆變器負載輸出電壓和電流波形。加入積分復位器前,諧振逆變器在換流過程中開關損耗大,負載輸出電壓和電流尖峰明顯。 圖8 未加入積分復位器時的負載輸出波形 圖9為加入積分復位器后Delta調制諧振逆變器負載輸出電壓和電流波形。開關損耗明顯減小,負載電壓和電流波形尖峰消失。 圖9 加入積分復位器之后的負載輸出波形 本文研究了一種基于零電流開關串聯諧振逆變器的微網逆變器結構及控制策略,通過在傳統的電流可調Delta調節器中加入具有復位功能的積分器,進一步減小了輸出電流的穩態偏置值,同時保持紋波電流含量在一個較低的水平,瞬時響應超調量幾乎可以忽略。通過仿真分析和研制25 kW單相實驗樣機驗證了電流控制器的調節性能。 參考文獻: [1]李嘯驄,任子熠,袁輝,等.基于多指標非線性控制方法的微網逆變器控制設計[J].電力自動化設備,2017,37(9):18-23. [2]余暢舟,張興,劉芳,等.組串式LC型光伏逆變器并網諧波環流及其抑制策略分析[J].電力系統自動化,2016,40(13):77-84. [3]劉東奇,鐘慶昌,王耀南,等.基于同步逆變器的電動汽車V2G智能充放電控制技術[J].中國電機工程學報,2017,37(2):544-557. [4]姚廣平,張永盈,林康紅.一種適應電源頻變的晶閘管三相全控整流橋α角控制器[J].電測與儀表,2015,52(21):102-105. [5]陳堃,周友斌,徐華安,等.基于電壓控制的逆變器無互聯線并聯控制研究[J].電力電子技術,2017,51(1):82-85. [6]李燕青,王子睿.dq0坐標系下微網電壓電流雙閉環下垂控制方法及其逆變器設計[J].華北電力大學學報(自然科學版),2017,44(1):39-45. [7]王堅,王毅,胡燦,等.MMC型光伏并網逆變器無差拍控制策略[J].電力科學與工程,2017,33(9):8-14. [8]張學廣,馬彥,李瑞,等.兩相靜止坐標系下并網逆變器的重復控制策略[J].電工技術學報,2016,31(9):85-91. [9]甄文超. 基于Delta逆變器式三相串聯補償交流穩壓源的研究[D].內蒙古:內蒙古科技大學,2014. [10]李春來,劉衛亮,王印松,等.基于FPGA的微網儲能逆變器電壓逆控制方案實現[J].電力科學與工程,2016,32(2):43-49. [11]樊英,周曉飛,張向陽,等.基于新型趨近律和混合速度控制器的IPMSM調速系統滑模變結構控制[J].電工技術學報,2017,32(5):9-18. [12]嚴廣,蔡世冠,張旭,等.電網不平衡下PWM整流器滑模變結構控制[J].電力電子技術,2017,51(1):1-3. [13]陸翔,謝運祥,桂存兵,等.基于多滑模變結構控制的三相PWM整流器非線性控制[J].電工技術學報,2016,31(4):79-87.2 采用積分復位的電流可調Delta調節器
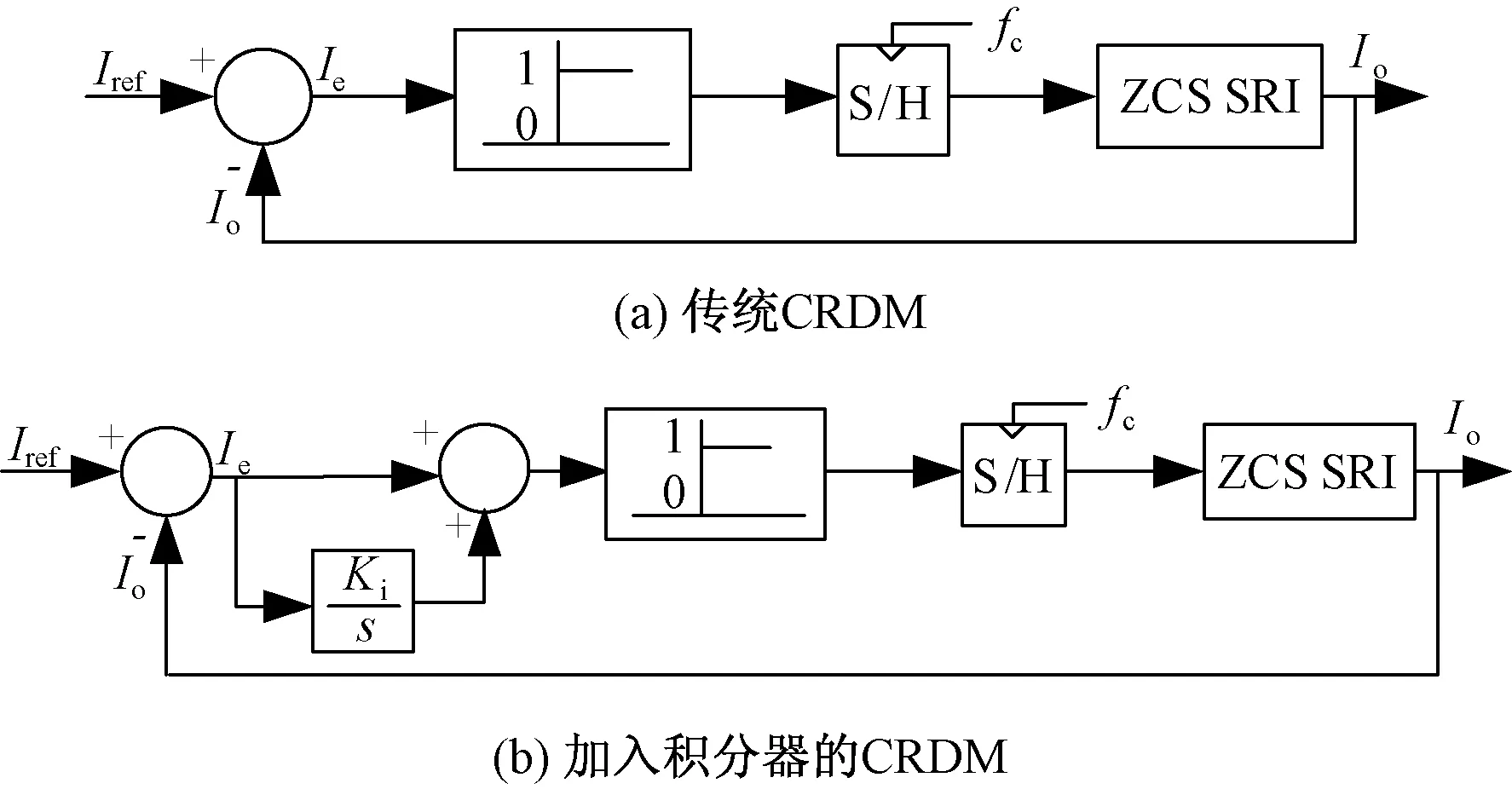
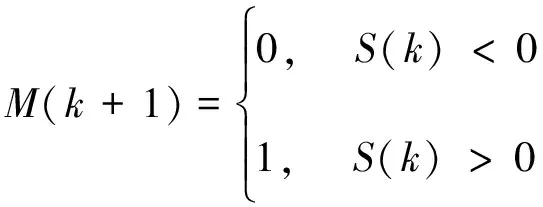
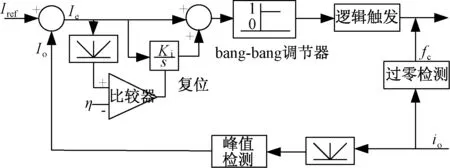
3 帶有復位功能的積分器設計
4 仿真過程分析
5 實驗結果
6 結論

