多變量過程閉環辨識在穩壓器中的應用

胡云波， 張 偉

(上海理工大學 光電信息與計算機工程學院，上海 200093)

0 引言

穩壓器是核電場反應堆里十分重要的裝置之一，其穩定運行對整個核電站有著特別重大的意義。在對核電站的仿真控制中，準確建立穩壓器的數學模型是獲得理想控制效果的必要條件。實際情況中，穩壓器并不是單一的輸入輸出系統，其壓力與液位之間存在著復雜的耦合關系[1]，這也為穩壓器的模型辨識帶來了許多阻礙。在過去的幾十年里，陸續涌現了許多相關的辨識方法，并逐漸形成了使用帶噪聲的觀測數據對模型的未知參數實現建模優化的形式[2]，比如遞推最小二乘法[3,4]、人工神經網絡[5]、常微分方程法[6]、以及在輸出信號加以處理后建立基于偏差補償系統的建模方法。這些方法雖然能實現模型的辨識，但需要外加測試信號，勢必對原模型造成干擾，導致過程輸出超出約束范圍。本文提到的閉環辨識方法[7]，不用額外加入測試信號，只要系統能夠穩定運行，通過系統的輸入、輸出數據就可以將模型辨識出來。

1 穩壓器系統

1.1 穩壓器工作原理

壓水堆核電站中穩壓器在一回路的具體位置[8]如圖1所示。

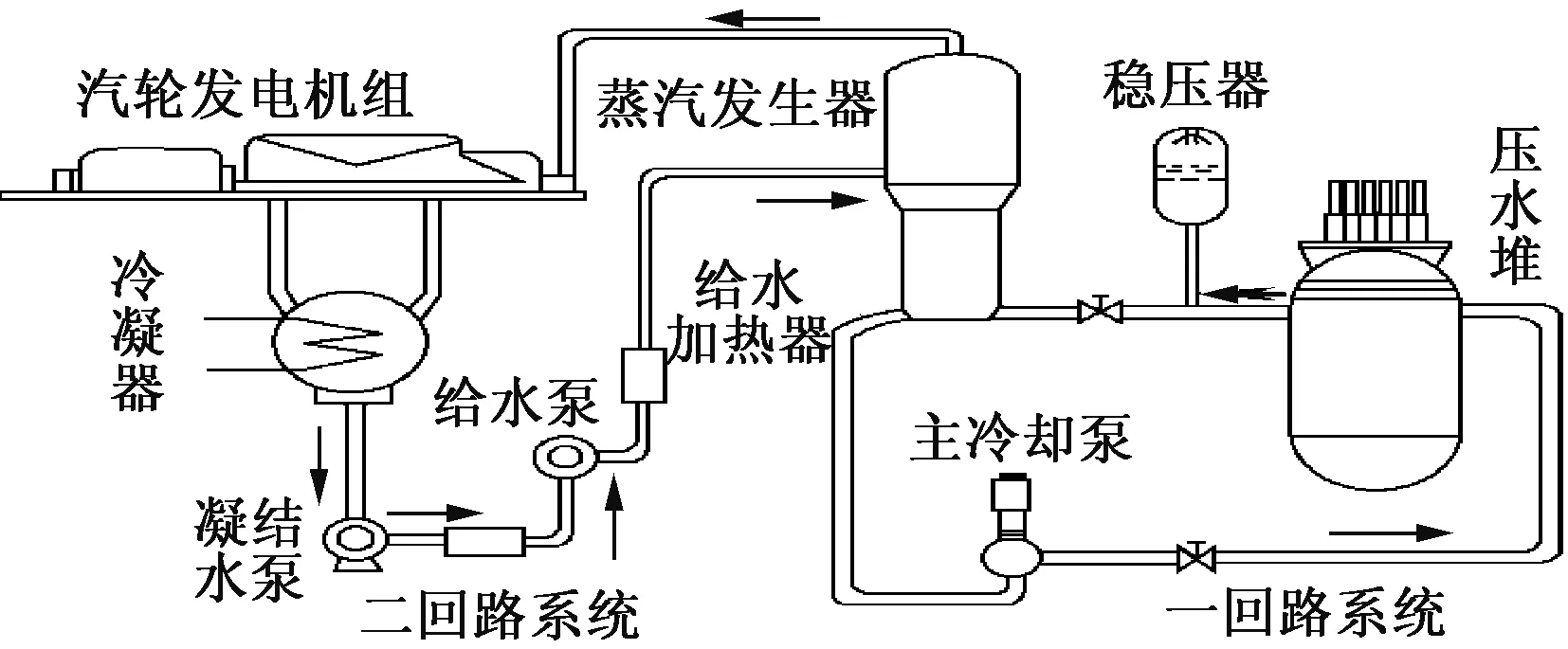
圖1 壓水堆核電站工藝流程圖

一回路中設備的壓力由穩壓器內的蒸汽壓力來表示。穩壓器的功能主要是調節整個系統中冷凝劑的壓力,確保核電站在穩定運行時整個回路中的壓力值在設定值附近浮動,防止回路中因為壓力太高致使核電廠設備損壞,或者壓力太低導致穩壓器中液體沸騰,致使反應堆堆芯散熱故障，發生重大安全事故[9]；當穩壓器的壓力值大于預先設定的值，系統將會自動將安全閥門打開，使穩壓器內的壓力值降低，使其穩定在安全閾值內。穩壓器的控制系統由兩個獨立的控制系統組成。系統的壓力主要由噴淋閥加熱器以及氣體釋放閥來控制。當系統正常穩定運作時,穩壓器中的液體與氣體維持在某個平衡狀態。當噴淋閥中噴淋出冷水時,穩壓器上方的蒸汽因為噴淋的冷水而凝結成液體，沿著穩壓器內壁向下流入液體部分,穩壓器內蒸汽的壓力由此減小;而當加熱器工作后,穩壓器下方液體空間的部分液體受熱變為蒸汽蒸發到穩壓器內部上方的蒸汽空間,此時穩壓器內的壓力上升。而穩壓器液位則主要由上充閥門和下瀉閥門開合度來控制。

1.2 穩壓器耦合被控對象簡化模型

將該系統簡化為雙輸入雙輸出模型[10]，搭建穩壓器耦合控制系統的數學模型如圖2所示，兩個輸出變量是：上充閥門和下泄閥門的流量差值、電加熱器的功率值。通常假設下泄閥門的值保持不變，那么電加熱器功率值、上充閥的流量即為系統的兩個輸入變量，而系統的輸出變量則分別是穩壓器的壓力與水位。

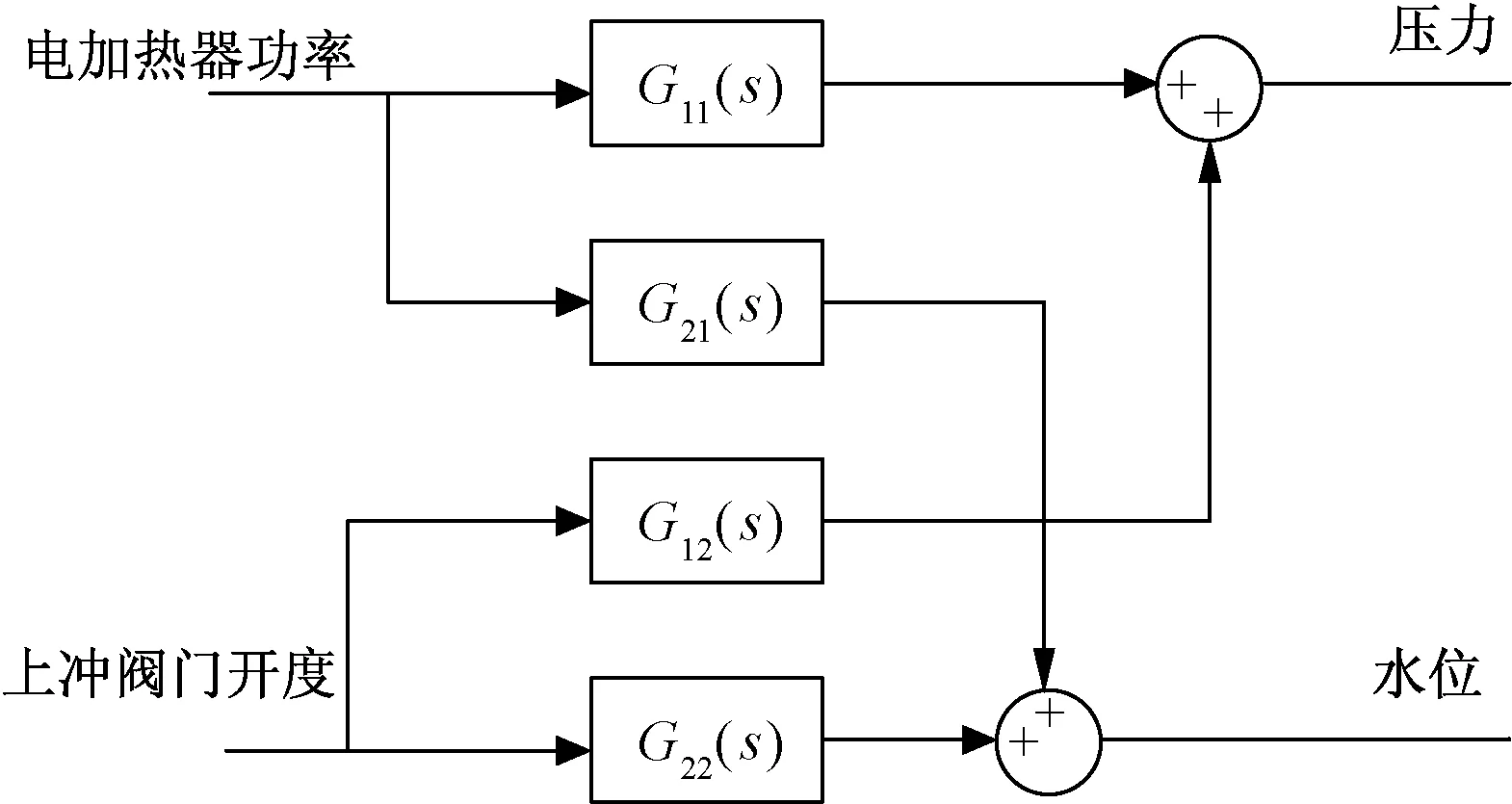
圖2 穩壓器的數學模型結構圖

穩壓器壓力降低時，電加熱器會加大功率，使穩壓器內的水受熱蒸發為水蒸汽，增加穩壓器內部蒸汽部分的壓力。相反，壓力過高時，加熱器功率降低，噴淋閥的噴淋量會增加，促使穩壓器內部的蒸汽凝結成水，降低穩壓器內的壓力值；當穩壓器內的水位出現偏差時，穩壓器會及時地調整上充閥門和下泄閥門的流量，確保水位在閾值范圍內。

2 多變量過程模型辨識方法

2.1 過程對象頻率響應矩陣

假設一個n輸入n輸出的多輸入多輸出系統，如圖3所示，圖中ri(i=1,2,…,n)是系統設定值，ui(i=1,2,…,n)是控制量，yi(i=1,2,…,n)是被控變量，K(s)、G(s)分別為控制器和被控對象。

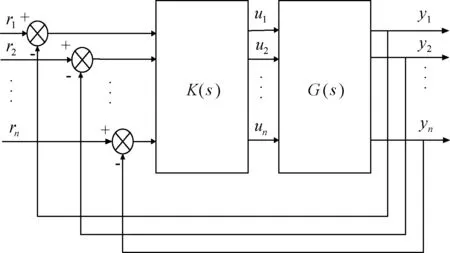
圖3 多變量控制系統框圖

(1)

當系統設定值ri發生變化時, 那么被控量yi和控制量ui都會從之前已經穩定的狀態逐漸過渡，達到新的穩態。這些信號都可分解為

yi(t)=Δyi(t)+ysi

(2)

ui(t)=Δui(t)+usi

(3)

式中: Δyi(t),ysi與Δui(t)，usi分別為yi和ui的瞬態及穩態部分。假設設定值r1先發生變化,并維持其它值不變;記錄所有控制量ui(t)和被控量yi(t)的變化過程,直到它們達到新的穩態狀態。這樣,Y1(s)和U1(s)滿足如下關系：

Y1(s)=G(s)U1(s)

(4)

接著改變設定值r2，并保持其余設定值不變，重復前面步驟，直至n個設定值全部發生變化，即可得到下面的表達式：

[Y1(s)，…，Yn(s)]=G(s)[U1(s)，…，Un(s)

(5)

由于Uk(s)(k=1,2,…,n)線性無關，所以傳遞函數G(s)可以表示為：

G(s)=[Y1(s)，…，Yn(s)]×

[U1(s)，…，Un(s)]-1

(6)

經過拉氏變換、替換和化簡，用jω替換式(6)中的s，可以得到G(jω)表達式。

2.2 傳遞函數矩陣模型

由多變量過程對象的頻率響應，可以得到傳遞函數矩陣中的各個元素，傳遞函數矩陣中的每個元素采用二階加純滯后模型：

(7)

式中：系數a,b,c以及L的值可由下列表達式計算得出：

|G(jωl)|2c2=1

(8)

(9)

將式(8)(9)改寫成矩陣形式，即：

φθ=Γ

(10)

其中

式中：θ可以通過最小二乘法得到，即

θ=(φTφ)-1φTΓ

(11)

那么模型的參數就可以從θ中獲得

(12)

上文提到的辨識方法能夠用于多輸入、多輸出系統的PID控制以及復雜控制系統解耦控制中，并達到很好的效果。在系統里，系統的輸入、輸出變量一一對應。該辨識方法也能在預測控制系統中使用，輸入輸出變量根據個數不同可以分為不同的系統。如果輸入變量的個數少而輸出變量的個數多時，此時系統成為瘦系統，系統已知的數目將比控制變量的個數多，改變已知量能確保變量Uk(s)(k=1,2,…,n)不是線性相關的，則該變量組成的矩陣一定是可逆的；而當控制變量的個數大于已知數目，系統變為胖系統，變量Uk(s) 的相關性就不能確定，則由Uk(s)組成的矩陣是否可逆便不確定。但是在現場，對于胖系統而言，控制系統的預測通常是將多余控制量的值保持固定為最優解，則已知數目等于控制變量的個數，也可將其視為瘦系統，符合本文使用該辨識方法的前提。

3 模型辨識驗證

模型辨識精度可以由辨識誤差來量化：

(13)

為了驗證本文中提到的方法的可行性，引入一壓水堆核電站穩壓器的數學模型[11]加以驗證。一壓水堆核電站穩壓器的數學模型傳遞函數如下：

辨識結果顯示其參數誤差E=4.1%。

本文中提到的方法在穩壓器系統辨識中有很好的辨識度，利用這種辨識方法得出的模型能直接用于多變量控制器的設計，比如穩壓器模型的解耦控制器設計等。

4 結論

本文針對穩壓器模型辨識中耦合系統辨識精度低，魯棒性不高的問題，引入了一種多變量過程閉環辨識方法。首先得到穩壓器的水位和壓力的被控特性，并搭建耦合數學模型，通過對運行中的系統產生的信號加以頻譜分析，獲得穩壓器模型的頻譜響應矩陣，最終通過遞推最小二乘法擬合出系統參數。實驗表明，這種方法能有效的辨識出穩壓器的模型，在工程上具有可行性，為核電站的控制仿真提供了便利，提高了運行的安全性。

參考文獻：

[1] 錢虹,周蕾,房振魯.壓水堆核電站穩壓器壓力和水位的解耦控制研究[J].核科學與工程,2017,37(1):5-11.

[2] 毛曉芳,侯力,馬登秋,等.燃氣輪機載荷動力系統優化建模仿真[J].計算機仿真,2017,34(10):49-54.

[3] 張海寧.基于遞推最小二乘算法的逆變器參數辨識[J].電力科學與工程,2017,33(2):21-27.

[4] 丁鋒,汪菲菲.損失數據線性參數系統的遞推最小二乘辨識方法[J].控制與決策,2016,31(12):2261-2266.

[5] 蘇一新,馬彥會,石倩,等.基于BP神經網絡模型的磁懸浮水泵PID參數優化[J].流體機械,2018,46(1):20-24.

[6] 邱舒婷,張志祥.解常微分方程程序的蛻變測試方法[J].艦船電子工程,2016,36(12):29-33.

[7] 王亞剛,許曉鳴.復雜多變量過程模型的閉環頻域辨識[J].控制與決策,2010,25(6):825-830.

[8] 馬進,劉長良,李淑娜.穩壓器壓力水位控制系統建模與仿真[J].核科學與工程,2010,30(1):9-14.

[9] 許志斌. 核電站穩壓器機理建模分析及控制研究[D].廣州:華南理工大學,2016.

[10] 董化平,張倬,孫啟航,等.壓水堆核電廠穩壓器壓力和水位控制系統仿真研究[J].自動化與儀器儀表,2017(1):138-141.

[11] 張國鐸. 基于智能控制理論的壓水堆穩壓器控制系統的研究[D].上海:上海電力學院,2013.