無線電調頻引信諧波提取改進算法

劉非凡，劉忙龍，曹少珺

(機電動態控制重點實驗室， 西安 710065)

在無線電調頻引信的定距算法中，諧波提取是整個算法不可或缺的一部分[1]，諧波提取的處理精度和實時性直接影響定距算法最終的定距性能，因此對諧波提取算法的設計顯得至關重要[2-3]。

目前的研究中，ARM芯片已成功替代傳統模擬電路結構，在引信的信號處理、信號采集領域得到了應用[4]。由于ARM芯片自身屬于馮諾依曼結構，只能對數據進行串行處理，因此處理時間相對較長[5]。文獻[6]通過短時傅里葉變換對信號時域進行分段諧波提取，又利用重疊采樣的方法減小的采樣間隔，保證了諧波提取的處理精度。由于采樣樣本的重疊，大大增加了需要處理的數據總量，因此降低了諧波提取算法的實時性。為了解決實時性不足的問題，文獻[7]采取了簡便算法，即只對信號的頻率進行大致的估算，以此來推導引信與目標的相對距離。該方法有效提升了實時性，但算法的簡化卻降低了處理精度。若能在保證處理精度的前提下提升實時性，會使諧波提取算法的處理能力明顯提升。本文針對ARM芯片在無線電引信高處理精度的定距算法中處理速度不足的問題，提出了諧波快速提取改進算法。

1 諧波提取算法及重疊采樣方法

1.1 基于短時傅里葉變換的諧波提取算法

根據無線電調頻引信的原理，炮彈與目標的相對距離與發射信號和回波信號的差頻頻率有關[8]。但由于差頻信號不規則區的存在，導致差頻頻率無法直接反應距離的變化。要想得到炮彈與目標的相對距離，需對差頻信號進行時頻域轉換，在頻域得到其各次諧波的幅值，并通過對諧波的幅值進行連續的觀察，最終得到彈目相對距離隨時間的變化關系[9]。為得到諧波幅值隨時間的連續變化關系，通常采用短時傅里葉變換對差頻信號進行處理。即利用相同的窗函數在時域上連續對采樣信號進行截取，將采樣信號分為若干個采樣段，再對各采樣段分別進行傅里葉變換得到其各自的頻域波形。

但短時傅里葉變換的采樣方法自身存在缺陷，每個短時變換的窗函數過窄，窗內的信號采樣點數量不夠，會導致頻率分析不夠精準，頻率分辨率差。窗函數過寬，時域上又不夠精細，時間分辨率低[10]。

1.2 重疊采樣方法

如前文所述，傳統采樣方法中各次傅里葉變換之間時間間隔較大，由此造成了信號處理的精度較低，現有的改進方法中，保持采樣點數為 1 024點不變，每組傅里葉變換的起始點之間間隔32個采樣點，而非之前間隔 1 024點進行采樣(如圖1所示)。此種采樣方法中的采樣點會在不同的傅里葉變換中重復利用，各采樣段的窗函數會在時域上發生重疊，增加運算量。但因為減小了起始點與起始點之間的采樣間隔，提高了短時傅里葉變換的等效采樣頻率。等效采樣頻率由之前的1 kHz提升到了32 kHz，隨著等效采樣頻率的提高，處理精度也得到了提升。

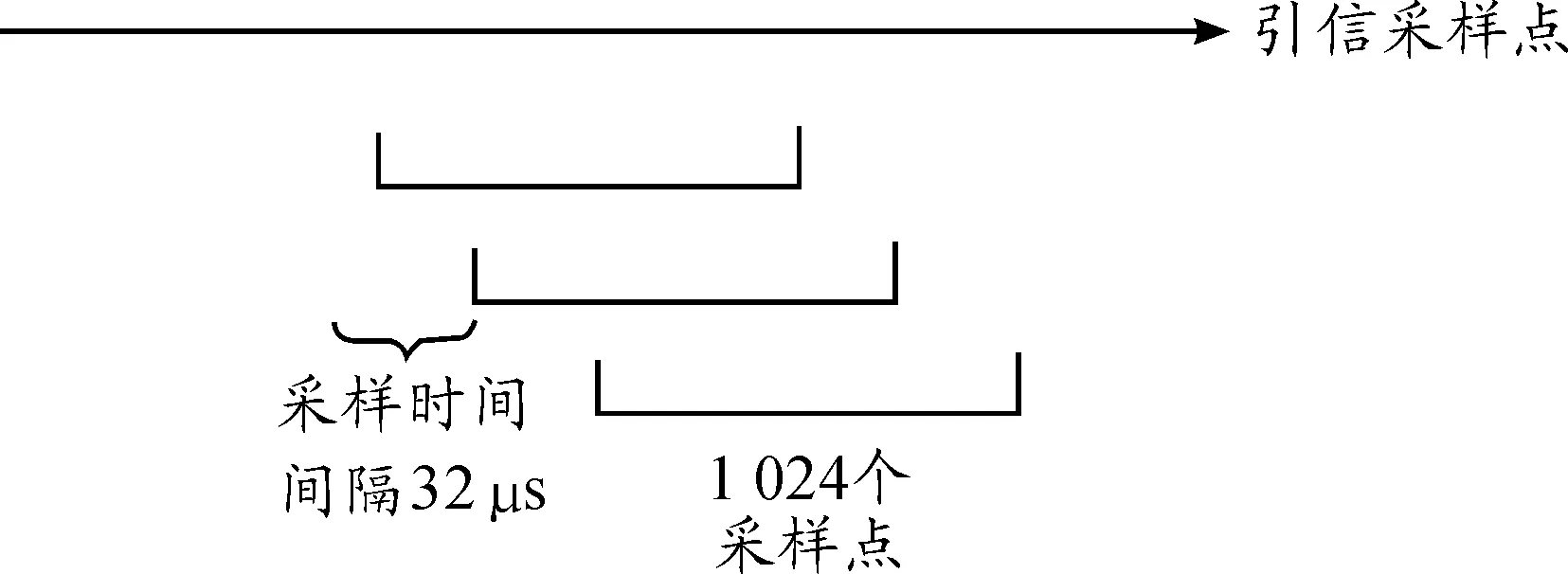
圖1 重疊采樣方法示意圖

1.3 重疊采樣對實時性的影響

通常情況下，處理短時傅里葉變換各段數據最有效的手段是對其分別進行快速傅里葉變換(FFT)。但快速傅里葉變換耗費系統資源較多，加之重疊采樣方法數據量過大，若按重疊采樣方法進行采樣，雖然處理精度得到了滿足，但處理實時性嚴重降低。以本文選用的STM32F407芯片為例，該芯片以ARM cortex M4作為內核，并自帶DSP模塊。STM32F407芯片可以使用自身DSP庫中的快速傅里葉變換函數進行1 024點的快速傅里葉變換。該函數由芯片生產廠家提供，內部程序已經過反復優化。因此可以認為該函數處理時間為STM32F407芯片快速傅里葉變換所能達到的最快速度。該函數進行一次快速傅里葉變換平均需耗時0.58 ms。若按前文所述的重疊采樣的方法進行采樣，一秒鐘的采樣時間內共獲得了31 969個采樣段，每個采樣段都包含 1 024個采樣點。對每個采樣段分別進行快速傅里葉變換提取諧波，共需處理時間18 542.02 s。此處理時間遠大于采樣時間一秒鐘，完全不能滿足信號實時處理的需要。因此，需要對快速傅里葉變換算法進行進一步的改進。

2 無線電調頻引信諧波快速提取改進算法

前文提到的重疊采樣算法已可以滿足諧波提取算法的精度要求，為了在不降低處理精度的前提下提高實時性，需要從理論層面對算法運用的公式進行等效代換，削減不必要的計算量。本文利用離散傅里葉變換(DFT)和復數運算的性質對原有算法進行改進。

離散傅里葉變換的公式為：

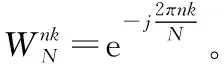
(1)

根據前文所述的采樣方案，需后移M個點(M

(2)

現保留式(1)中第M項到第N項的復數乘法運算結果，用x(N+1)—x(N+M)替換掉式(1)中x(1)—x(M-1)，得到如下等式：

(3)

對式(3)進行進一步整理,得：

(4)

因為最終求得的是對應點的幅值，因此要對X(k)進行取模運算。對向量相加后的和向量求模時，運算結果只與相加前各向量的長度以及向量之間的相對夾角度數有關，而與向量自身的角度無關。式(2)與式(4)中各項復數的模值均相等，各項間的夾角亦為定值且相等，因此對式(2)與式(4)整體取模后|X2(k)|=|X3(k)|。

而式(4)中，x(M+1)—x(N)對應項的值均與式(1)中的對應項相等，需要進行復數乘法計算的只有x(N+1)—x(N+M)的對應項，即只需進行M次復數乘法就可完成新一輪DFT運算。因此應用式(4)計算方法代替式(2)后，可大大減小程序整體的運算量，提高運算速度。

綜上，該算法利用離散傅里葉變換和復數運算的性質，對重疊采樣中重復元素的計算結果進行反復利用，即不再對未處理采樣段中重復元素進行二次計算，而是直接使用已處理采樣段中重復元素的計算，避免了重復計算，以此提升諧波提取算法的運算速度。

3 實驗驗證

3.1 Matlab仿真驗證

第一節介紹的基于重疊采樣的短時傅里葉變換已可以滿足諧波提取的精度要求。利用Matlab軟件進行仿真，分別運行改進前的諧波提取算法和改進后的算法，若改進后的算法對諧波的提取結果與改進前一致，則可以說明改進后的算法能夠滿足諧波提取算法處理精度的要求。

本仿真實驗選取采樣頻率為1 MHz的無線電調頻引信推板實驗數據，數據共5 632 000個采樣點。兩種算法均采用短時傅里葉變換進行信號四次諧波的提取，改進前的算法采用快速傅里葉變換對各采樣段進行處理，改進后的算法利用第二節所述的方法對各采樣段進行處理，每個采樣段均為1 024個點。實驗結果如圖2、圖3所示。

從圖2及圖3可以看出，兩種算法計算出的差頻信號四次諧波的宏觀走勢完全一致，改進算法的細節分辨率也不低于改進前的算法，兩組實驗對信號的處理結果相同，說明改進算法確實不會降低諧波提取的處理精度。

3.2 引信芯片實測

使用C語言編寫改進算法，利用以ARM為內核的STM32F407芯片運行該程序。統計程序運行時間，并與Matlab的處理結果進行比較。STM32F407芯片利用DSP庫中自帶的基4快速傅里葉變換函數arm_cfft_radix4_f32()，對上述數據進行一次1 024點的快速傅里葉變換共需耗時 0.58 ms，而改進算法的單次傅里葉變換僅耗時0.019 ms，完成全部176 000次傅里葉變換共耗時3.283 s。按前文所述，數字信號處理芯片在一秒中的時間內最少需要完成 31 969次運算才能滿足實時性的最低需求，而改進算法平均一秒鐘可完成53 610次運算，完全符合實時性的要求。

將STM32F407芯片的處理結果導入Matlab，生成與時間的關系圖，處理結果如圖4所示。將圖4與圖2及圖3對比可以看出，在使用相同算法的情況下，STM32芯片的處理結果與Matlab的處理結果完全一致，數據實際處理結果與理論仿真結果相符。改進算法在保證了處理精度前提下有效提升了信號處理的實時性。

圖2 FFT與改進算法的時間與幅值關系

圖3 FFT與改進算法的時間與幅值局部關系

圖4 STM32處理結果

4 結論

本文提出的無線電調頻引信諧波快速提取改進算法，是指利用離散傅里葉變換和復數的運算性質，對重疊采樣中重復元素的計算結果進行反復利用，即不在未處理的采樣段中對重復元素進行二次計算，而是直接使用已處理采樣段中重復元素的計算結果，在不改變信號最終處理結果的前提下削減了計算量，減少了短時傅里葉變換即諧波提取算法的運算量。通過仿真及實驗驗證表明：進行一次1 024點的快速傅里葉變換處理耗時0.58 ms，而改進算法的單次傅里葉變換僅耗時0.019 ms。改進算法的實際性能與理論分析結果一致，與以前的算法相比運算效率得到了提升，可在不降低信號處理精度的前提下縮短信號處理所需的時間，解決了在處理精度過高時，以ARM為信號處理芯片的引信諧波提取算法實時性不足的問題。

[1] 彭業凌.線性調頻引信信號的分選和識別[D].北京：北京理工大學,2015.

[2] 盧新棟,李艷萍.調頻引信信號處理器模塊化改進[J].制導與引信,2014,35(2):14-17.

[3] 張偉.基于ARM的雷達信號處理系統的研究[D].南京：南京理工大學,2008.

[4] 張晨.基于ARM微處理器的引信數據采集系統設計[D].南京：南京理工大學,2014.

[5] STM32F40x和STM32F41x產品手冊[Z].意法半導體,2012.

[6] 高磊.寬帶雷達中頻回波長脈沖壓縮采樣重構中的分段重疊處理及其機理分析[J].信號處理,2011,27(7):967-974.

[7] 鞏艷華.基于STM32的連續波線性調頻引信系統設計與實現[J].科技信息,2014(9):71.

[8] 崔占忠,宋世和.近炸引信原理[M].北京：北京理工大學出版社,2009.

[9] 趙慧昌.無線電引信設計原理與方法[M].北京：國防工業出版社,2012.

[10] 盧廣闊.基于短時分數階傅里葉變換的譜分割算法[J].電波科學學報,2017,32(4):474-481.