基于TR MIMO雷達的相干目標DOA估計*

劉夢波，胡國平，師俊朋，周 豪

(空軍工程大學防空反導學院，西安 710051)

0 引言

時間反轉(zhuǎn)技術[1-4]是基于靜態(tài)媒質(zhì)中波動方程的空間互易性和時間對稱性，在復雜多散射環(huán)境下，利用多徑分量進行相干疊加，對其他雜波信號進行非相干疊加，從而獲得良好的空-時聚集性能。目前，時間反轉(zhuǎn)技術應用較多的領域為MIMO通信系統(tǒng)。

近年來，越來越多的學者將TR技術應用到雷達系統(tǒng)中，其中文獻[5-8]將TR技術應用到雷達中，顯示其獨特的性能優(yōu)勢。相比于傳統(tǒng)的MIMO雷達[9-10]，TR MIMO雷達應用傳輸波形到多徑的環(huán)境中，從而產(chǎn)生一種相對簡單的自適應編碼方法[11],并且改善信道的信噪比(SNR)和提高DOA估計的速率。因此，可以改善克拉美-羅界，提高DOA估計的性能[12]。在許多的應用場合中，特別是在MIMO雷達的應用中，相干目標的DOA估計問題都是一個重要的問題。為了克服目標的相干問題，已經(jīng)提出了很多種方法，例如：RD-ESPRIT(reduced dimensional ESPRIT)算法[13]，F(xiàn)BSS-MUSIC(forward-backward spatial smoothing-MUSIC)算法，ESPRIT-like算法[14]和Toeplitz矩陣算法[15]。然而，之前的算法過于復雜并且應用于低空環(huán)境時估計性能并不理想。

文中提出一種新的解相干方法，根據(jù)TR MIMO雷達接收信號模型構造Toeplitz矩陣，利用優(yōu)化迭代的方法進行相干目標的DOA估計，提高了估計的精度，降低了計算復雜度。仿真結果證明了此種方法的優(yōu)越性。

1 MIMO雷達信號模型

假設收發(fā)分置MIMO雷達的發(fā)射端為M個，接收端為N個，陣元間距為d(波長的一半)，陣列為垂直均勻線陣。假設空間中存在K個目標，目標滿足遠場條件，此時發(fā)射波與反射波的俯仰角近似相等設為θk(k=1，2，…，K)。則MIMO雷達接收回波時接收到的信號矩陣為：

(1)

式中:βk是目標散射系數(shù);fk為多普勒頻移；at(θk)=[1,…,e-jπ(M-1)sinθk]T為發(fā)射波的導向矢量;ar(θk)=[1,… ,e-jπ(N-1)sinθk]T為反射波的導向矢量；s(t)=[s1(l) ,s2(l),…,sM(l)]T為M個陣元的發(fā)射信號矩陣，其中，l=0,…,L表示快拍數(shù)；W(t)為N個陣元接收到的噪聲矢量，設該噪聲矢量是均值為0，方差為σ2的高斯白噪聲，且各陣元接收到的噪聲互不相關。

2 TR MIMO雷達信號模型

根據(jù)時間反轉(zhuǎn)的原理，將式(1)中接收端信號矩陣取共軛并且時間反轉(zhuǎn)，進行能量歸一化，再次發(fā)射出去。發(fā)射信號模型為εX*(-t)，則TR MIMO接收端的信號矩陣為：

(2)

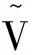
(3)

(4)

(5)

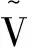
對接收信號Y(t)進行匹配濾波：

(6)

將信號矩陣Z(t)向量化，則Z(t)可改寫為：

(7)

式中:vec(·)是將一個矩陣向量化，“°”表示Khatri-Rao積。其中，

噪聲通過匹配濾波器的統(tǒng)計特性為：

(8)

(9)

所以式(7)可以改寫為：

(10)

3 構造Toeplitz 矩陣

由于相干目標使接收信號的協(xié)方差矩陣的秩小于目標數(shù)，從而使基于特征值結構的算法不能直接做相干源的DOA估計。為了去除目標間的相干性，根據(jù)TR MIMO接收信號模型，采用Toeplitz 矩陣重構的方法構造無秩虧的矩陣，達到解相干的效果。定義：

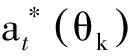
(11)

C(2M-1)×(2M-1)

其中，diag(·)表示對角矩陣。

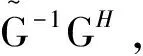
(12)

根據(jù)式(12)，可以構建一個Toeplitz矩陣，該矩陣可以表示為：

(13)

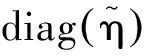
4 DOA估計

對式(13)進行特征值分解，可以得到：

(14)

式中：Σs是一個對角線上元素為K個最大的特征值的對角矩陣；Σn是一個對角線上的元素為剩下的(M-K)個最小的特征值的對角矩陣；Us和Un分別是信號子空間和噪聲子空間。因為信號子空間與噪聲子空間是正交的關系，則：

(15)

根據(jù)Q的最小值，從而獲得DOA估計：

(16)

下面，使用一種迭代的方法來提高估計的性能：

步驟1根據(jù)式(16)得到初始值為θ0。

步驟2根據(jù)一階近似理論來遞推估計量θ(i)，根據(jù)文獻[16]有：

(17)

(18)

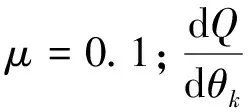
步驟3重復上述的過程，直到兩次迭代值之差小于一個門限為止：

Q(i+1)-Q(i)≤ν

(19)

式中ν=0.001Q(i)為一個合理的門限值。

5 仿真實驗

仿真實驗中，收發(fā)分置的MIMO雷達為垂直均勻線陣，陣元間距為發(fā)射信號波長的0.5倍，且各個陣元發(fā)射相互正交的信號。為了分析算法的統(tǒng)計性能進行300次Monte Carlo仿真。

圖1為M=8，N=10，目標數(shù)為3，信噪比SNR=10 dB的仿真圖。圖中，當快拍數(shù)較高時，文中的算法比其他幾種算法有較低的計算復雜度。其中，文獻[17]為信號矩陣進行降維轉(zhuǎn)化處理的算法和文中算法計算復雜度相當，明顯優(yōu)于FBSS-MUSIC和文獻[14]中的ESPRIT-like算法。在快拍數(shù)較低的情況下，文獻[17]中的算法甚至優(yōu)于文中的算法。

圖2為使用文中算法進行的30次DOA估計，其中陣元數(shù)M=8，N=10，目標數(shù)為3，信噪比SNR=10 dB。從圖中可以看出，文中算法可以準確地估計出相干目標的DOA。

圖3為在不同的信噪比條件下，采用迭代算法的TR MIMO雷達與傳統(tǒng)MIMO雷達和不使用迭代方法的TR MIMO雷達的均方根誤差的比較。其中，陣元數(shù)M=8，N=10，目標數(shù)為3，快拍數(shù)為100。從中可以看出，TR MIMO雷達可以提高DOA估計的性能，具有較小的均方根誤差。使用迭代的方法可以降低均方根誤差，進一步提高估計精度。

圖4表明在快拍數(shù)為100，目標數(shù)為3的條件下，均方根誤差隨著發(fā)射和接收陣元的增加而不斷減小，即系統(tǒng)的DOA估計性能不斷地加強。

圖5為在不同信噪比條件下，4種算法的均方根誤差的比較。其中，陣元數(shù)M=8，N=10，目標數(shù)為3，快拍數(shù)為150。可以看出，在信噪比較低的情況下，文中的算法均方根誤差明顯更低，即有更好的估計精度。

6 結論

文中介紹了一種新的TR MIMO雷達相干目標的DOA算法。算法根據(jù)MIMO雷達接收信號模型，利用時間反轉(zhuǎn)理論，導出了TR MIMO雷達的接收信號模型。基于導出的信號模型，采用Toeplitz矩陣重構算法，從而解決了目標的相干問題。在角度估計時采取了基于一階近似理論的優(yōu)化迭代方法，進一步提高了雷達DOA估計精度，同時降低了計算復雜度。仿真實驗表明，文中提出的算法能夠克服目標間相干性，實現(xiàn)精確的DOA估計，且算法復雜度更低。