基于模型參考自適應的天線罩誤差斜率估計*

金鵬飛，于劍橋，艾曉琳，馬安鵬

(1 北京理工大學宇航學院，北京 100081； 2 淮海工業集團有限公司，山西長治 046012)

0 引言

對于雷達制導體制的自尋的導彈，雷達反射信號經過導引頭天線罩會產生折射，進而產生瞄準線誤差角。瞄準線誤差角會降低制導回路的穩定性，增大導彈脫靶量[1]。對天線罩誤差進行估計和補償，消除其帶來的不利影響已成為熱點問題。

研究人員采用了多種方法來補償天線罩誤差。內廓面修磨法[2]，對天線罩內廓面進行修磨，但這種方法往往受限于工藝水平。文獻[3]利用粒子群優化算法來優化修磨方案，降低了對修磨經驗的要求。建立補償表的方法是在地面測試中預先標定天線罩誤差，在導彈飛行中進行插值補償[4]。這種方法雖然簡單，但導彈飛行時的環境與地面不同，使得該方法適應性不強[5]。文獻[6]利用擴展卡爾曼濾波來估計天線罩誤差斜率。文獻[7]在制導回路中引入抖動信號，可以估計出天線罩誤差斜率，但高頻抖動信號會影響彈體穩定性。

文中建立天線罩寄生回路的離散模型，將其作為參考模型，估計模型作為可調系統，利用模型參考自適應估計出被控對象的參數，進而估計出天線罩誤差斜率。針對參數自適應律中參數難以選取的問題，改進自適應算法，提高了在線估計方案的可行性。

1 天線罩寄生回路建模

雷達反射信號經過天線罩發生折射，導致真實目標視線偏移到了虛假目標視線位置。圖1給出了天線罩誤差作用下的彈目視線幾何關系[8]。其中，真實彈目視線角為qt，天線罩造成的虛假彈目視線角為q*，真實目標視線與虛假目標視線的夾角Δq稱為天線罩的瞄準線誤差角，簡稱為天線罩誤差。導引頭指向角為qs，導引頭指向與真實彈目視線之間的誤差角為ε，導引頭指向與虛假彈目視線之間的夾角為ε*，彈體姿態角為?，導引頭框架角為φr，水平線為xI。

天線罩誤差隨導引頭框架角的變化曲線為天線罩瞄準曲線，表達式為Δq=f(φr)。曲線的斜率為天線罩誤差斜率，記為R，即：

(1)

由圖1可知，測得的虛假視線角為：

q*=qt+(qs-?)R

(2)

在穩定跟蹤的前提下，導引頭的指向角與虛假彈目視線角之間的跟蹤誤差較小，可以認為qs≈q*，簡化式(2)可得：

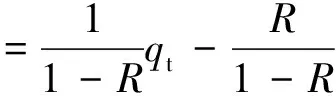
(3)

由式(3)可知，在制導回路中，彈體姿態角速度通過天線罩誤差斜率反饋到了導引頭處，形成了包含導引頭、制導濾波器和駕駛儀在內的天線罩寄生回路。圖2為基于比例導引制導律的天線罩寄生回路簡化模型。

圖2中，N為導航比，vc為彈目相對速度，vm為導彈速度，Tg為制導控制系統時間常數，Tα為攻角滯后時間常數，n為系統動力學階數。取n=4，天線罩寄生回路的閉環傳遞函數為：

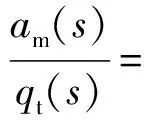
(4)

由式(4)知，天線罩誤差斜率改變了閉環系統特征方程的一次項和常數項系數，使得系統的極點發生了變化。天線罩誤差斜率會對制導回路的穩定性產生影響，從而影響導彈的無量綱脫靶量[9]。給定一組系統參數如表1所示。

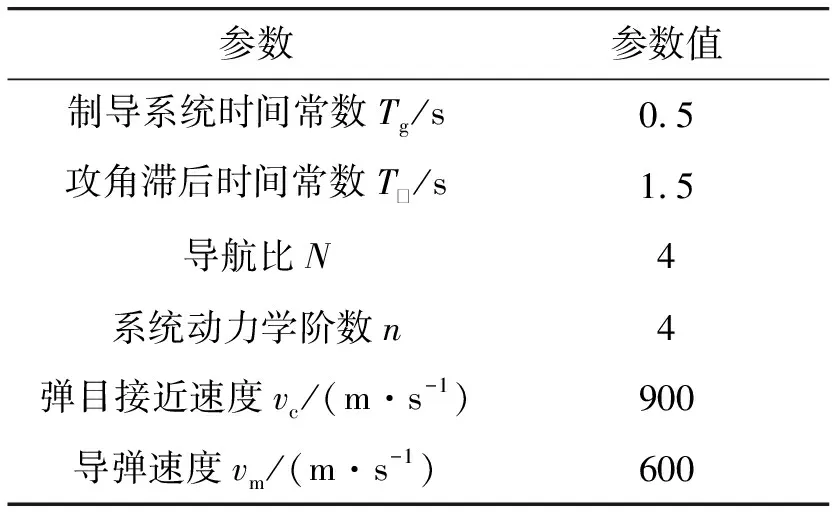
表1 制導系統參數

考慮實際過程，取采樣時間T=0.01 s，R=-0.1，對式(4)進行帶零階保持器的Z變換，得到被控對象的離散模型：

(5)

根據被控對象分子分母的階次，設被控對象的估計模型為：

(6)

式中：a1,a2,a3,a4,b0,b1,b2,b3為模型參數估計值。

2 在線估計方案

2.1 模型參考自適應理論

模型參考自適應控制系統一般含有三部分：參考模型、可調系統和自適應機構。在控制系統設計中，參考模型一般是理想模型，可調系統是被控對象。如果把被控對象作為參考模型，并聯估計模型作為可調系統，則可以得到圖3的結構，這種結構可用于系統參數辨識。

文中采用基于Popov超穩定性理論的模型參考自適應控制系統設計方法。設參考模型為：

(7)

式中：θm=[am1,…,amn,bm0,…,bmm]T，xm=[ym(k-1),…,ym(k-n),yr(k),…,yr(k-m)]T，分別為參考模型的參數向量和輸入輸出數據向量；ym(k)和yr(k)分別為參考模型的輸出和輸入。

可調系統為:

(8)

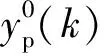
(9)

自適應機構包含一個產生信號υ(k)的線性補償器，即:

(10)

對應的自適應調節律為[10]：

(11)

其中，式(10)和式(11)中的di(i=1,2,…,n)的選擇應使得離散傳遞函數。

(12)

為嚴格正實函數。當系統階次較高時，di需要較繁雜的計算。并且，將模型參考自適應算法應用于系統參數辨識時，參考模型的am是未知的辨識參數，di的選取將無法進行。在這種情況下，對自適應算法進行改進。

2.2 算法改進

將可調參數向量和觀測數據向量進行擴展：θpe(k)=[ap1(k),…,apn(k),bp0(k),…,bpm(k),-d1(k),…,-dn(k)]T,xp(k-1)=[yp(k-1),…,yp(k-n),yr(k),…,yr(k-m),ε(k-1)，…,ε(k-n)]T。這樣，需要設計者選取的di包含在自適應調節的參數里面。得到改進算法的參數自適應調節律為：

(13)

式中:λ為大于0.5的常數;H矩陣需保證初始值為正定對稱矩陣。

2.3 在線估計方案

以R=-0.1為例，將被控對象式(5)作為參考模型，式(6)為并聯可調系統。在線估計方案具體為：對兩個系統給予相同輸入，獲取輸出信號，并得到誤差信號。誤差信號輸入自適應調節律，調節可調系統的參數，當誤差收斂時，可調系統的參數也將收斂于參考模型的系統參數。最后，由系統參數辨識結果得到天線罩誤差斜率的估計值。

3 仿真驗證

取自適應調節律中λ=1，H=I9×9，θpe(0)=0，輸入信號為均值是0、方差是1.5的白噪聲。應用改進的模型參考自適應算法對被控對象模型參數進行辨識，圖4和圖5是參數辨識結果，圖6和圖7是參數辨識誤差曲線。

可以看到，隨著時間進行，參數辨識結果趨向真值附近穩定，誤差曲線收斂到零，辨識的效果良好。

由于R的存在改變了傳遞函數中的一些系數值，可以根據對應關系計算出R的值，這里選取b3的值來進行換算，其值始終保持與R=0時b3的值成1/(1-R)倍的關系。估計結果和誤差分別如圖8和圖9。

可以看到，R的估計值接近真值，估計誤差很快收斂到零。

下面考察R為方波變化時，本方案的估計效果。取R=-0.12+0.02(-1)k，k=t/4，k取整。此時的參考模型為每一時刻的被控對象，取λ=80，其他參數不變。R的估計結果和估計誤差分別如圖10和圖11。

在R突變的時刻，R的估計值和估計誤差會有較大偏差，但隨后估計誤差可以較快收斂到零，仍然可以準確估計R。仿真結果驗證了將模型參考自適應算法應用于天線罩誤差斜率的在線估計這一方案的可行性。

4 結論

文中的研究表明，將模型參考自適應算法應用于天線罩誤差斜率的估計是有效和可行的。將導彈制導回路作為參考模型，并聯估計模型作為可調系統，通過模型參考自適應辨識出被控對象系統參數，進一步得到天線罩誤差斜率的估計值。同時，改進的自適應算法很好的避免了參數自適應調節律中參數的預選取問題，極大簡化了設計過程，更易于實現，為天線罩誤差斜率的在線估計提供了新的思路，但對于快時變誤差斜率的估計效果還需要作進一步的優化。