兩步自適應快速濾波算法測量火箭彈滾轉角*

閆小龍，陳國光，田曉麗, 董曉芬，趙福春

(1 中北大學，太原 030051； 2 山東特種工業集團有限公司，山東淄博 255201)

0 引言

在制導火箭彈的飛行過程中，為了準確對火箭彈的飛行軌跡進行控制，姿態角的獲取是非常重要的。如今使用陀螺儀、星敏傳感器、GPS以及磁強計來測量滾轉姿態角[1]。磁強計以成本低，受外界干擾小而被廣泛應用。然而，這種傳感器測姿時存在較多的誤差因素，限制了滾轉角測量的精度。因此，在正確測量火箭彈滾轉角前，必須對磁強計及測量電路進行校準補償。目前，研究人員已經提出了很多的解決方案。黃琳等人使用UKF濾波方法離線校準磁傳感器的靈敏度偏差，從而給出每個磁傳感器對應的補償值[2]。Da Forno等人分別使用UKF與EKF對磁強計的靈敏度和基線偏移進行在線校準[3]。盧兆興等人提出使用自適應遺傳算法校準磁強計的靈敏度[4]。文中提出的算法對雙軸磁強計的測量幅值、雙軸基線偏移、靈敏度、非正交角進行在線校準。磁強計五個參數的校準使測量值更為準確；兩步快速算法使得在線快速校準成為可能。

1 滾轉姿態角測量模型

使用雙軸磁強計測量制導火箭彈滾轉角時，在火箭彈橫截面上安裝了雙軸磁強計測量組件。通過角度關系的轉換，可以得到火箭彈的滾轉姿態角。

圖1是基于磁強計的角度測量模型。紅色方塊代表雙軸磁強計測量組件。其中，O-xynz為測量坐標系，OX為彈軸矢量，Oy和Oz是磁強計的兩個理論正交的敏感軸。δ是非正交誤差角，OZm為載體零位參考軸，OZ為慣性空間零位參考軸，Hyz是火箭彈當地地磁場矢量在Oyz上的投影，由全球地磁場模型給出，γ為載體旋轉姿態角。φ0是磁強計的安裝誤差角，φ是制導火箭彈的滾轉姿態角。

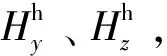
(1)

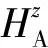
記φs=φ-φ0，則

(2)

火箭彈的滾轉姿態角可得

γ=αH-φ0-φs

(3)

通過濾波方法估計參數實際上是將參數估計的問題轉化為狀態估計的問題，可以將濾波過程中關注的參數增加到狀態向量中，在濾波過程中實時估計，根據濾波的狀態向量與設定真值進行對比，從而判斷濾波過程及結果的正確性。

濾波的系統狀態方程與量測方程如式(4)和式(5)所示：

Xk+1=f(Xk,uk)+Wk

(4)

Hk+1=h(Xk+1)+Vk+1

(5)

式中：Xk+1為狀態向量，Hk+1為量測向量。f為線性向量函數，h為非線性向量函數，Wk為系統方程噪聲向量，Vk+1為量測方程噪聲向量，uk為確定性控制項[5]。

濾波過程中被估計的參數向量為：

(6)

為了準確而精簡地描述火箭彈的滾轉運動，考慮到火箭彈在飛行過程中所需要的飛行參數以及在飛行過程中的加速度變化很小，所以這里假設火箭彈的滾轉運動為加速度緩慢變化的加速運動。

(7)

在公式(7)中，Φ,Φ′,Φ″分別代表火箭彈的滾轉角位移，角速度和角加速度，下標“i”表示第i個采樣周期對應的數據。

2 濾波器初值的兩步快速自適應調整

在卡爾曼濾波算法中，狀態向量初值的準確性決定著濾波器的收斂速度[6]。然而，由于不同的磁強計，不同的安裝方法及安裝工藝導致狀態向量中的參數具有不同的真值，所以狀態向量的初值是不確定的。為了加快濾波器的收斂速度，需要將濾波器的初值盡可能快的精確到一個較小的范圍內。

2.1 第一步：磁強計校準參數的快速調整

捷聯在彈體截面上的雙軸磁強計在火箭彈飛行時，Y軸和Z軸的軌跡方程為：

(8)

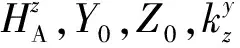
在這一步驟中，校正參數擬合的精度越高，意味著UKF收斂速度越快，但是擬合精度的提高與擬合時間的消耗并非成正比關系。因此，當擬合精度提高的速度接近濾波器收斂的速度時需要適當的判斷條件來終止這一過程。

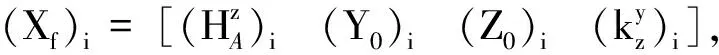
(Λf)i=(Xf)i-(Xf)i-1

(9)

擬合參數的協方差矩陣為:

(10)

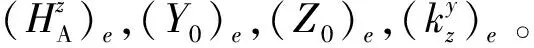
2.2 第二步：滾轉運動的快速調整

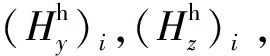
(11)

結合式(7)有下列關系：

(12)

同樣，在考慮解算速度要求高于解算精度要求的前提下，當滾轉角參數殘差最小時取為濾波初值，對Φ,Φ′,Φ″進行參數擬合，定義殘差為：

(13)

當ε取到最小值時，火箭彈的滾轉參數Φ,Φ′,Φ″取得最優值。

與第一步相同，在第二步中，參數擬合的精度與擬合的時間并非成正比。當擬合精度提高的速度接近濾波收斂的速度時需要一個類似的停止策略。

(Λs)i=(Xs)i-(Xs)i-1

(14)

擬合參數的協方差為：

(15)

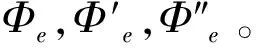
3 具有加性噪聲的增強無跡卡爾曼濾波算法

為了提高現有濾波算法的性能，文中提出了快速收斂噪聲隱含的擴維無跡卡爾曼濾波算法。文中提出新的TAUKF算法，該算法在UKF中包含模型誤差預測，增加了系統狀態下的驅動噪聲，以擴大系統狀態的輸入信息。所提出的算法克服了傳統UKF系統模型誤差對濾波性能的影響，增強了濾波過程的魯棒性。擴展系統狀態，增加了UKF模型中狀態向量的維數。考慮到驅動噪聲對系統運動模型的影響，噪聲被加到系統狀態中。因此，擴展狀態向量和協方差矩陣可以表示為：

(16)

(17)

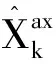
(18)

(19)

(20)

時間傳播方程為：

(21)

(22)

狀態估計方程為：

(23)

(24)

量測估計方程為：

(25)

(26)

互協方差矩陣為：

(27)

計算UKF增益：

(28)

最后，更新狀態矩陣和協方差矩陣：

(29)

4 算法模擬仿真

測量火箭彈的滾轉運動，對磁強計和測量電路進行仿真建模。火箭彈在實際飛行過程中，磁強計和測量電路的工作參數不能準確的獲取。而在模擬過程中，這些誤差參數都可以進行人為調整。只有這樣才能將最終的數據處理結果與正確的數據進行對比，用來評估算法的優勢。

分別使用傳統UKF方法和文中提出的TAUKF算法對磁場測量組件進行參數校準和火箭彈的角度測量。

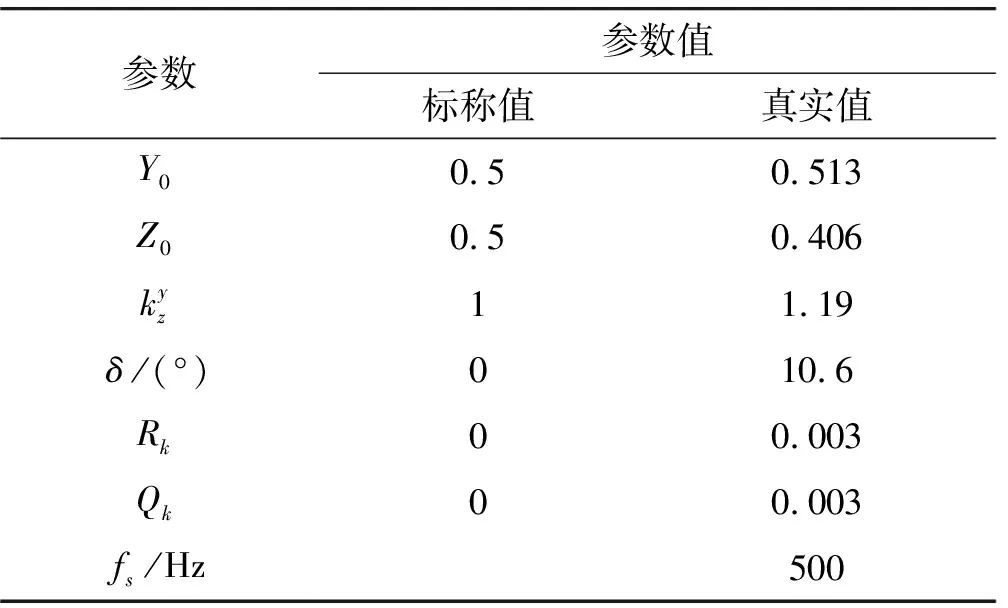
參數參數值標稱值真實值Y00.50.513Z00.50.406kyz11.19δ/(°)010.6Rk00.003Qk00.003fs/Hz500

由圖2(圖中FS為“Full Scale”的縮寫，代表滿量程)我們可以看到，TAUKF在0.11 s左右完成了濾波算法的初值擬合，并將濾波算法的初值調整到非常接近真值的精度。在后續濾波階段大約0.15 s左右，濾波器狀態向量中校正參數接近真值，校正參數值設為最優恒定值。開始小計算量的UKF濾波。通過對比可以看出，TAUKF較UKF在收斂速度上有著較明顯的優勢。

在滾轉角信息的輸出結果看來，提出的TAUKF算法同樣在收斂速度上要遠遠的高于現有的UKF算法。并且在500 Hz采樣頻率的前提下，提出的TAUKF算法可以在接收數據0.17 s左右就可以提供0.023 rad精度的角位移，0.07 rad/s精度的角速度，以及0.08 rad/s2精度的角加速度。而傳統的UKF算法想要提供該精度下的滾轉角信息則需要49 s左右的信號處理時間。

5 結論

在該研究中，提出了一種TAUKF濾波算法，用于在線快速估計火箭彈的滾轉姿態角。有效地解決了旋轉導彈在發射后不能及時獲取滾轉姿態而無法機動的問題。該算法通過對磁場測量組件的校正參數的確定，以及實時的量測結果，計算火箭彈的滾轉姿態角。在滾轉姿態角的實時處理過程中，該算法對濾波器的初值進行自適應獲取，極大的加快了濾波器的收斂速度與精度。并且在磁場測量組件的校正參數確定后，對濾波器的狀態向量的校正參數賦予確定值，在很大程度上減少了彈載計算機的運算量，為彈上其他信息的計算留出空間。