隨機競爭Lotka-Volterra系統的正周期研究

蒲曉琴

(中國民航飛行學院 計算機學院, 四川 廣漢 618307)

1 基礎知識

經典的Lotka-Volterra系統是通過下面的n維微分方程來描述物種間的相互制約的,

n≥1,i=1,2,…,n,

(1)

其中,bi(t)、aij(t)(i,j=1,2,…,n)都是連續函數.環境噪聲存在于人口系統中.事實上,許多學者已經研究了人口系統受白噪聲干擾的問題[1-17].對于確定性的人口系統,有許多文獻對周期解的存在性進行了研究.然而對隨機微分方程周期解的研究[17]還非常的少.

文獻[17]考慮了如下n-維隨機人口系統:

n≥1,i=1,2,…,n,

(2)

其中，bi(t)、aij(t)和cij(t)(i,j=1,2,…,n)是周期為T>0的連續函數.令(Ω,F,{Ft}t≥0,P)是一完全概率空間{Ft}t≥0≥0,

ω(t)=(ω1(t),…,ωn(t))T

是定義在(Ω,F,{Ft}t≥0≥0,P)上的n-維Brownian運動.他們得到了對方程(2)漸進穩定周期解存在性的一些有趣結果.然而,文獻[18]所提出的一些結論是錯的.下面列出一些例子.首先,文獻[18]中定理2.1的證明,把‖(u1,…,un)‖→∞對每個i有ui→∞或ui→-∞.因此,文獻[18]中定理2.1的條件并不能推出Lv→-∞,其中

其次,文獻[18]中定理2.2的證明,有

Lv=

但是作者把公式弄錯了，應該是：

Lv=

因此,對方程(2)漸進穩定周期解存在性問題依然未得到解決.本文得到了方程(2)周期解存在性和全局吸引性的充分條件.即使在特殊情況下,也改進了文獻[9]中的結果.

注1.1隨機過程ξ(t)=ξ(t,ω),t∈R,如果其有限維分布是T周期性的,那么Rn也被認為是T周期性的,對任意正整數m和任意時刻t1,…,tm,隨機變量ξ(t1+kT),…,ξ(tm+kT)的聯合分布與k(k=±1,±2,…)無關.顯然,如果ξ(t)是周期為T的隨機過程,則其時刻也是以T為周期的.

2 正解的存在性和唯一性

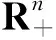
Rn={x∈Rn:xi>0,1≤i≤n},

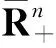
令R+=[0,+∞),E[f]是指f的期望.

為了方便起見,記:

其中f(t)為周期為T的連續函數.對任意的常序列{δij}(1≤i≤n,1≤j≤n)定義

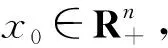
假設(A) 設

aii(t)>0,aij(t)≥0,

i≠j,t≥0,i,j=1,2,…,n.

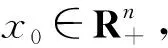
證明首先考慮方程:

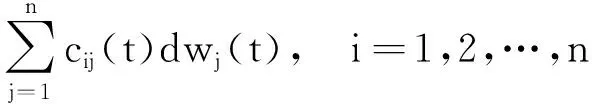
(3)

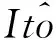
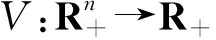
它的非負性可以由下面的式子得到:

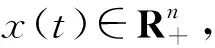
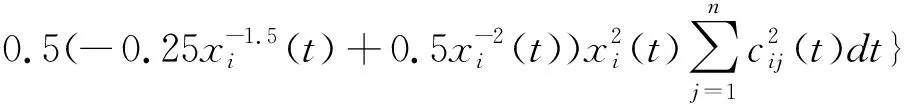
由假設(A)可得:

故

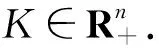
因此有

ELV(x)≤K.

從上面和文獻[20]中的推論4可得τe=∞,證畢.

3 正周期解的存在性

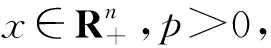
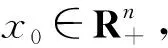
E‖x(t,x0)‖p≤K,t≥0,

其中p為某個正常數.

證明為了方便,記x(t)=x(t,x0).定義

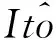
dV(x(t))=LV(x(t))dt+

計算

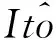
d(etV(x))=et(V(x(t))dt+dV(x(t))).

因此可以得到:

etEV(x(t))≤V(x0)+

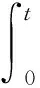
V(x0)+K(et-1),t≥0.

這意味著

EV(x(t))≤V(x0)e-t+K,t≥0.

由引理3.1有

E(‖x(t)‖p)≤

證畢.

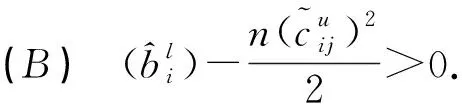
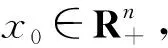
其中θ為正常數且滿足

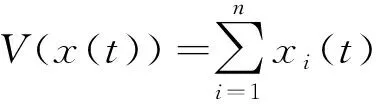
d[(1+U(t))θ]=θ(1+U(t))θ-2J(t)dt-

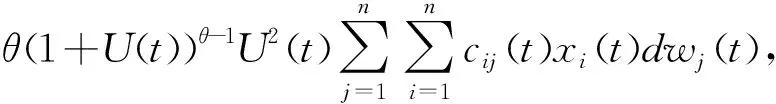
(4)

其中

不難估計

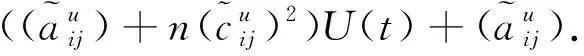
(5)

從(4)和(5)式可得

d[eηt(1+U(t))θ]=ηeηt(1+U(t))θdt

+eηtd[(1+U(t))θ]≤

eηt(1+U(t))θ-2{η(1+U(t))2-

eηtG(U)dt-θ(1+U(t))θ-1U2(t)×

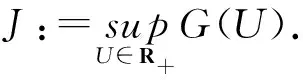
E[eηt(1+U(t))θ]=(1+U(0))θ+

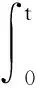
然后有

E[Uθ(t)]≤E[(1+U(t))θ]≤

設

因此

證明完畢.

引理3.4[22]如果μn,n=1,2,…,n,μ是Rn上的測度,那么以下條件是等價的：

(i) 測度μn序列弱收斂于μ;

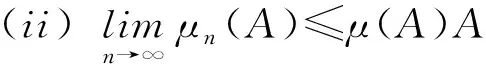
令

p(0,x0,x(t),A)=P(x(t)∈A|x(0)=x0),

定理3.1在假設(A)和(B)下,方程(2)有一個正周期解.

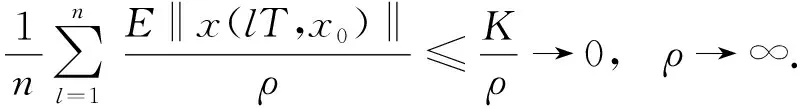
(6)

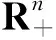
由(6)式知,這個序列是弱收斂的.令Pnk為其子序列弱收斂于某一測度P0.如文獻[24]中的定理3.2.2,證明了測度P0滿足方程:

因此定義了周期過程的初始分布.由引理3.3和Chebyshev不等式知道對任意0<ε<1,存在

使得

Pn(‖x(t,x0)‖≤δ)=

引理3.4暗示P0(‖x(t,x0)‖≤δ)≤ε.因此,這個周期解是非平凡的.

注3.1定理3.1意味著如果方程(2)具有至少一個有界解,則對于一些(通常是隨機的)的初始條件,方程(2)有周期解.對于n=1,也遵循Massera定理.當然,這個結果不能保證方程(1)對應的確定性方程周期解的存在性,因為周期性隨機過程不需要具有周期性的樣本函數.

4 正周期解的全局吸引性

本節將獲得方程(2)的周期解的全局吸引性的充分條件.

令x(p)(t)為方程(2)的一個正-T周期解.

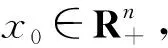
說x(p)(t)是全局吸引的.

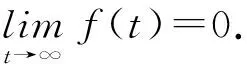
引理4.2在假設(A)下,方程(2)的解x(t),t≥0,是一致連續的.

證明記

σij(t,x(t))=cij(t)xi(t),i,j=1,2,…,n,

和

f(t,x(t))=(f1(t,x(t)),…,fn(t,x(t)))T,

σ(t,x(t))=(σij(t,x(t)))n×n.

計算

從這個式子和引理3.2

E(‖f(t,x(t)‖)p)≤K, ?p>0,

(7)

E(‖ρ(t,x(t))‖p)≤K, ?p>0.

(8)

結合(7)、(8)式和文獻[26]中的引理3.4,知道方程(2)的解是一致隨機連續的.

注4.1文獻[26]中引理3.4的證明,若p=4,我們得到下面的不等式

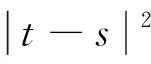
(9)

換句話說,對指數γ,幾乎所有的樣本路徑都是局部的,但都是一致H?lder連續的.因此x(t)的幾乎每一個樣本路徑在t≥0時都是一致連續的.

對任意常數v1,…,vn,令

很容易看出hi(i=1,2,…,n)都是周期為T的函數.

介紹下面這個假設:

假設(C) 存在正常數v1,…,vn使得函數hi(i=1,2,…,n)在[0,T]為正的.

定理4.1在假設(A)、(B)和(C)下,方程(2)的正T-周期解x(p)(t)是全局吸引的.

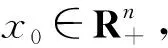
因此,直接計算出函數V(t)的右上導數d+V(t)有

將(10)式從0到t積分,得到

V(0)<∞,

這使得

因此,從引理4.1和注4.1可得,

這就完成了定理4.1的證明.

文獻[8-9]考慮了隨機非自主邏輯方程

dN(t)=N(t)[a(t)-b(t)N(t)]dt+

α(t)N(t)dB(t),

(11)

其中B(t)為1-維標準Brownian運動,a(t)、b(t)和α(t)是周期為T的連續函數,a(t)>0,b(t)>0.

很容易從定理4.1中得到以下推論.

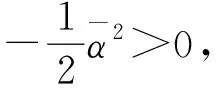
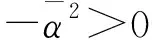
這就是注1.1中1/N*(t)或E[1/N*(t)]與周期T的關系.很明顯推論4.1改進了文獻[9]中的結果.

[1]BAHARA,MAOX.StochasticdelayLotka-Volterramodel[J].JMathAnalAppl,2004,292(2):364-380.

[2]BAHARA,MAOX.Stochastichybriddelaypopulationdynamics[J].IntJPureApplMath,2006,11(4):377-399.

[3]MAOX.Delaypopulationdynamicsandenvironmentalnoise[J].StochDynam,2005,5(2): 149-162.

[4]MAOX,MARIONG,RENSHAWE.EnvironmentalBrowniannoisesuppressesexplosionsinpopulationdynamics[J].StochasticProcessAppl,2002,97(1):95-110.

[5]MAOX,MARIONG,RENSHAWE.AsymptoticbehaviorofthestochasticLotka-Volterramodel[J].JMathAnalAppl,2003,287(1):141-156.

[6]PANGS,DENGF,MAOX.Asymptoticpropertyofstochasticpopulationdynamics[J].DynamContinDiscreteImpulsSystSerAMathAnal,2008,15(5):603-620.

[7]JIC,JIANGD,SHIN,O’REGAND.Existence,uniqueness,stochasticpersistenceandglobalstabilityofpositivesolutionsofthelogisticequationwithrandomperturbation[J].MathMethodsApplSci,2007,30(1):77-89.

[8]JIANGD,SHIN.Anoteonnonautonomouslogisticequationwithrandomperturbation[J].JMathAnalAppl,2005,303(1):164-172.

[9]JIANGD,SHIN,LIX.Globalstabilityandstochasticpermanenceofanon-autonomouslogisticequationwithrandomperturbation[J].JMathAnalAppl,2008,340(1):588-597.

[10]KHASMINSKIIRZ,KLEBANERFC.LongtermbehaviorofsolutionsoftheLotka-Volterrasystemundersmallrandomperturbations[J].AnnApplProbab,2001,11(3):952-963.

[11]ZHUC,YING.OnhybridcompetitiveLotka-Volterraecosystems[J].NonlinearAnal,2009,71(2):1370-1379.

[12]ZHUC,YING.OncompetitiveLotka-Volterramodelinrandomenvironments[J].JMathAnalAppl,2009,357(1):154-170.

[13]LIX,MAOX.Populationdynamicalbehaviorofnon-autonomousLotka-Volterracompetitivesystemwithrandomperturbation[J].DiscreteContinDynSyst,2009,24(2):523-545.

[14]LIX,GRAYA,JIANGD,MAOX.Sufficientandnecessaryconditionsofstochasticpermanenceandextinctionforstochasticlogisticpopulationsunderregimeswitching[J].JMathAnalAppl,2011,376(1):11-28.

[15]LIUM,WANGK.Persistenceandextinctioninstochasticnon-autonomouslogisticsystems[J].JMathAnalAppl,2011,375(2):443-457.

[16]LIUM,WANGK.Extinctionandpermanenceinastochasticnonautonomouspopulationsystem[J].ApplMathLett,2010,23(12):1464-1467.

[17]ZHANGB,GOPALSAMYK.Ontheperiodicsolutionofn-dimensionalstochasticpopulationmodels[J].StochAnalAppl,2000,18(2):323-331.

[18]YAGIA,TONT.Dynamicofastochasticpredator-preypopulation[J].ApplMathComput,2011,218(7):3100-3109.

[19]MAOX.StochasticDifferentialEquationsandApplications[M].Chichester:HorwoodPress,1997.

[20]XUD,YANGZ,HUANGY.Existence-uniquenessandcontinuationtheoremsforstochasticfunctionaldifferentialequations[J].JDiffEqns,2008,245:1681-1703.

[21]WUF,HUS,LIUY.PositivesolutionanditsasymptoticbehaviourofstochasticfunctionalKolmogorov-typesystem[J].JMathAnalAppl,2010,364(1):104-118.

[22]LEADBETTERMR,CAMBANISS.MeasureandProbabilityTheory:ABasicCourse[M].Carolina:UniversityofNorthPress,2002.

[23]BAINOVDD,KOLMANOVSKIIVB.Periodicsolutionofstochasticfunctionaldifferentialequations[J].MathJToyamaUniv,1991,14:1-39.

[24]HASMINSKIIRZ.StochasticStabilityofDifferentialEquations[M].Maryland:SijthoffandNoordhoff,1980.

[25]BARBALATI.Systemsd’equationsdifferentiald’oscillationsnonlineairies[J].RevRoumaineMathPuresAppl,1959(4):267-270.

[26]XUD,HUANGY,YANGZ.ExistencetheoremsforperiodicMarkovprocessandstochasticfunctionaldifferentialequations[J].DiscreteContinDynSyst,2009,24(3):1005-1023.