具有不變直線的可積非Hamilton系統的極限環分支

閆曉芳, 尚華輝, 楊紀華

(1. 永城職業學院 基礎部, 河南 永城 476600; 2. 寧夏師范學院 數學與計算機科學學院, 寧夏 固原 756000)

1 引言和主要結果

對于一個擾動可積非Hamilton系統

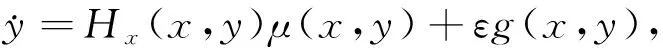
(1)

其中,0<|ε|?1,Hy(x,y)μ(x,y)和Hx(x,y)μ(x,y)是關于x、y的m次多項式,f(x,y)和g(x,y)是關于x、y的n次多項式,H(x,y)稱為系統(1)(ε=0)具有積分因子1/μ(x,y)的首次積分.假設未擾動系統(1)(ε=0)至少有一個中心,確定系統(1)極限環的個數和分布稱為Hilbert16問題[1],通過擾動一個系統的中心得到極限環是一種經典的方式.一般來說,研究從一個系統的中心周期環域分支出極限環的個數問題,共有4種方法:第一種是Poincare回歸映射法[2-3],第二種是Poincare-Pontryagin-Melnikov法(或稱為Abelian積分法)[4-7],第三種是可逆積分因子法[8-9],第四種是平均法[10-13].在平面上,第二種和第四種方法等價,見文獻[11].應用平均法研究系統(1)的極限環分支問題,由于需要做極坐標變換,所以目前文獻要求H(x,y)=x2+y2,例如文獻[10]研究了μ(x,y)=x+1的情形,文獻[11]研究了μ(x,y)是平面二次圓錐曲線的情形,文獻[12]研究了μ(x,y)=(x+a)(y+b)的情形.

本文研究如下擾動可積非Hamilton系統

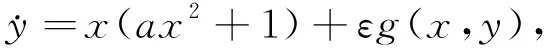
(2)

其中

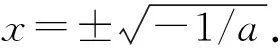
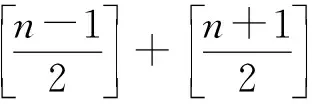
2 平均法和平均函數

首先介紹微分方程的平均法,更詳細的介紹參考文獻[6].

定理2考慮一個微分方程的初值問題

(3)

其中,F0(x,t)和G0(x,t,ε)是關于t的T-周期函數,x,x0∈U,T是不依賴于ε的常數,U是R中的開區間.定義平均函數

再考慮平均方程的初值問題

(4)

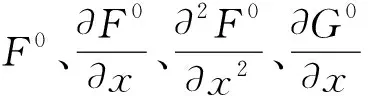
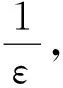
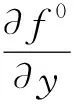
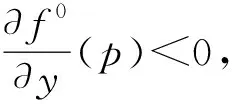
注1由定理2可知,如果方程(3)滿足定理中的條件,則平均函數f0(y)的一個簡單零點對應方程(3)的一個極限環.所以計算出平均函數f0(y)至關重要.

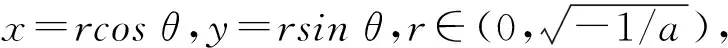
所以

ε2G0(r,θ,ε).

(5)

容易驗證,方程(5)滿足定理2中的條件.根據定理2,與方程(5)相對應的平均函數為

下面化簡平均函數f0(r),計算可得

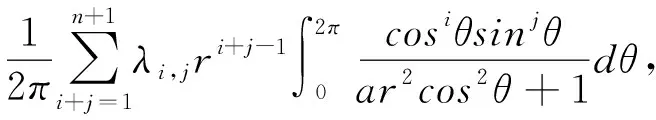
(7)

其中λi,j=ai-1,j+bi,j-1,這里假設λ0,0=a-1,j=bi,-1=0.因為ai,j和bi,j是任意的,所以λi,j也是任意的.定義

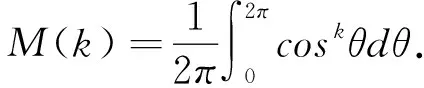
(8)

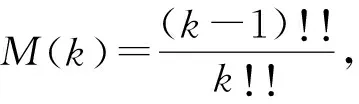
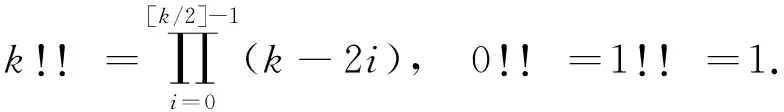
引理1下列關系式成立：

(i)Ii,2j+1(r)=0,

(ii)r2iI2i,0(r)=(-1/a)iI0,0(r)-

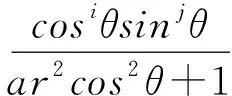
(ii)由

(ar2cos2θ)i-(-1)i=(ar2cos2θ+1)×

得

把上式兩端同時關于θ從0到π積分即可得(ii)成立.引理1證畢.

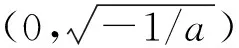
(9)

其中

因為λi,j是任意的,所以Ai,j也是任意的.又λ0,0=0,所以A0,0=0.再由(9)式和引理1中(ii)可得

其中

i=1,2,…,n-1.

(10)

注意到,當k是奇數時,M(k)=0,即β2k+1=0,所以

F(r)=α0[I0,0(r)+α/α0]+

(11)

注2由(9)式可知

所以

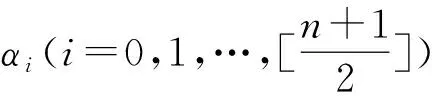
3 定理1的證明

首先把函數F(r)表示成若干個線性無關函數的線性組合.

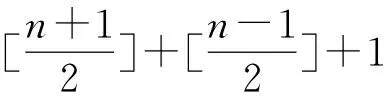
I0,0(r)+α/α0,r2I0,0(r),r4I0,0(r),…,

(12)

證明由(11)式知F(r)可以由(12)式中函數線性表出.所以只需證明它們是線性無關的即可.對于它們的任意線性組合

δ0(I0,0(r)+α/α0)+(δ1r2+δ2r4+…+

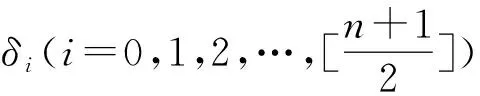
(δ0+δ1r2+δ2r4+…+

(13)

δ0+δ1(-1/a)+δ2a-2+…+

所以(13)式變為

為了證明本文中定理1,還需要下面引理,見文獻[14].

引理3考慮n+1個線性無關的解析函數hi:U→R,i=1,2,…,n+1,其中U?R是開區間.假設存在j∈{1,…,n+1}使得hj不變號,則存在n+1個常數ci,i=1,…,n+1,使得

在U中至少有n個孤立零點.

I0,0(r)+α/α0,r2I0,0(r),r4I0,0(r),…,

4 結論和展望

[1]ARNOLDVI.Tenproblemsin:theoryofsingularitiesanditsapplications[J].AdvSovietMath,1990,1:1-8.

[2]CHICONEC,JACOBSM.Bifurcationoflimitcyclesfromquadraticisochrones[J].JDiffEqns,1991,91(2):268-326.

[3]LICZ,LLIBREJ,ZHANGZF.Weakfocus,limitcyclesandbifurcationsforboundedquadraticsystems[J].JDiffEqns,1995,115(1):193-223.

[4]ATABAIGIA,NYAMORADIN,ZANGENEHH.Thenumberoflimitcyclesofaquinticpolynomialsystemwithacenter[J].NonlinearAnalysis,2009,71(7):3008-3017.

[5]YAOHY,HANMA.Thenumberoflimitcyclesofaclassofpolynomialdifferentialsystems[J].NonlinearAnalysis,2012,75(1):341-357.

[6]GASULLA,LICZ,TORREGROSAJ.Limitcyclesappearingfromtheperturbationofasystemwithamultiplelineofcriticalpoints[J].NonlinearAnalysis,2012,75(1):278-285.

[7]XIONGYQ.Thenumberoflimitcyclesinperturbationsofpolynomialsystemswithmultiplecirclesofcriticalpoints[J].JMathAnalAppl,2016,440(1):220-239.

[8]GIACOMINIH,LLIBREJ,VIANOM.Ontheshapeoflimitcyclesthatbifurcatefromnon-Hamiltoniancenters[J].NonlinearAnalysis,2001,43(7):837-59.

[9]VIANOM,LLIBREJ,GIACOMINIH.ArbitraryorderbifurcationsforperturbedHamiltonianplanarsystemsviathereciprocalofanintegratingfactor[J].NonlinearAnalysis,2002,48(1):117-36.

[10]LLIBREJ,RIOJ,RODRIGUEZJ.Averaginganalysisofaperturbatedquadraticcenter[J].NonlinearAnalysis,2001,46(1):45-51.

[11]GINEJ,LLIBREJ.Limitcyclesofcubicpolynomialvectorfieldsviatheaveragingtheory[J].NonlinearAnalysis,2007,66(8):1707-1721.

[12]BUICAA,LLIBREJ.Limitcyclesofaperturbedcubicpolynomialdifferentialcenter[J].Chaos,Solitons&Fractals,2007,32(3):1059-1069.

[13]COLLB,LLIBREJ,PROHENSR.Limitcyclesbifurcatingfromaperturbedquarticcenter[J].Chaos,Solitons&Fractals,2011,44(4):317-334.

[14]COLLB,GASULLA,PROHENSR.Bifurcationoflimitcyclesfromtwofamiliesofcenters[J].DynContinDiscreteImpulsSyst:MathAnal,2005,12(2):275-287.

[15]VERHULSTF.NonlinearDifferentialEquationsandDynamicalSystems[M].Berlin:Springer-Verlag,1996.