有限交換環上的Chowla定理

馬 寧， 彭國華

(四川大學 數學學院, 四川 成都 610064)

1948年,Vijayaraghavan等[1]證明了一個關于整數環上的完全剩余系的定理：設整數q>2，r1,r2,…,rn和s1,s2,…,sn分別是模q的兩組完全剩余系，則r1s1,r2s2,…,rnsn不是模q的完全剩余系．1954年，Coles等[2]利用數學歸納法又給出這一定理的一個簡單證明．1987年，孫琦等[3]將這一定理推廣到了Dedekind整環中．本文將Chowla定理推廣到一般有限含幺交換環．為此，定義了M-環，還討論了這類有限交換環的基本性質及判定的充要條件．

設R={r0,r1,…,rn-1}是一個有限含幺交換環，始終假定r0=0，相應地r1,r2,…,rn-1是R中的全體非零元素．若s0,s1,…,sn-1是r0,r2,…,rn-1的任意一個排列且s0≠0, 則存在k≥1使得sk=0.此時r0s0=rksk=0，集合S={risi|0≤i≤n-1}至多含有n-1個元素，從而S≠R．這表明，只要R不是零環[4]，則總存在r0,r1,…,rn-1的一個排列s0,s1,…,sn-1，使得S≠R．對于集合

S={risi|0≤i≤n-1}，

是否總有S≠R成立？

定義一個有限含幺交換環R為M-環，如果對于R中全體元素的任意一個排列s0,s1,…,sn-1，總有

{risi|0≤i≤n-1}≠R．

假設s0=0且R=Fq是q元有限域，q為一個素數的方冪，那么環R的乘法群

注意到方程Xq-1-1=0的解集為R×，有

所以q必為偶數．

若q為2的方冪，即R=F2m，m是正整數，則Frobenius映射σ(x)=x2是R上的自同構．取si=ri，i=0,1,…,q-1，則有

這表明R不是M-環．

定理1有限域是M-環的充要條件是它的特征為奇數．

設R=R1⊕R2⊕…⊕Rm是有限含幺交換環R的一個直和分解．對0≤i≤n-1，可以令

ri=(ri1,ri2,…,rim)，si=(si1,si2,…,sim)，

其中,rij,sij∈Rj，1≤j≤m．所以S=R當且僅當

Sj={rijsij|0≤i≤n-1}=Rj

對每個1≤j≤m均成立．于是，有

定理2設R為有限含幺交換環，則R是M-環的充要條件是其直和因子中至少有一個是M-環．

如下的結構性質保障了可以將一般的有限交換環分解成一些小的環的直和．

引理1任意有限含幺交換環可分解為有限交換局部環的直和．

Pi∩Pj=PiPj．

另一方面，R的冪零根

所以R的Jacobson根

但Nil(R)中的每個元素均為冪零元，J(R)是冪零理想．因此存在正整數t使得

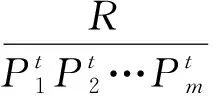
根據定理2和引理1，只需要討論有限局部交換環何時是M-環．

引理2若一個有限局部交換環不是域，則它是M-環．

證明設R={r1,r2,…,rn}是有限局部交換環．若R不是M-環，則存在r1,r2,…,rn的一個排列s1,s2,…,sn使得

S={risi|0≤i≤n}=R．

設P是R的唯一極大理想且|P|=k，則R恰有k個不可逆元，且Jacobson根J(R)=P為冪零理想．因此存在正整數n0使得Pn0=(0)．不失一般性，可設

r1,r2,…,rk∈P, rk+1,rk+2,…,rn∈R×,

則必有s1,s2,…,sk∈P且sk+1,sk+2,…,sn∈R×．否則，若存在j0>k，sj0∈P，則有

r1s1,r2s2,…,rksk,rj0sj0∈P

且這些元素兩兩不同.這與R恰有k個不可逆元的假設矛盾．于是

P={r1s1,…,rksk}?P2，

從而P=P2，故P=Pn0=(0)．這表明零理想是極大理想，R必為域，與假設矛盾．

定理3設R為有限含幺交換環，則R是M-環的充要條件是R不能分解為特征為2的有限域的直和．

證明由引理1，R=R1⊕R2⊕…⊕Rm，其中Ri(1≤i≤m)是有限交換局部環．若R不能被分解為特征為2的有限域的直和，則存在1≤i0≤m，使得Ri0不是域或者Ri0是奇特征的有限域．根據定理1和引理2，Ri0是M-環．再由定理2可知，R是M-環．

反之，若R是特征為2的有限域的直和，則由定理1和定理2可知，R不是M-環．

下面考慮定理3在置換多項式方面的應用．環R上的多項式f(X)∈R[X]稱為R的置換多項式，如果對應的多項式函數f:R→R誘導出R中元素的一個置換．有關有限交換環上的置換多項式及其應用的討論，可參考文獻[5-10]．因為一個置換多項式可以產生環中元素的一個置換，所以立即得到以下推論.

推論1M-環上的兩個置換多項式的乘積不再是置換多項式．

[1] VIJAYARAGHAVAN T, CHOWLA S. On complete residue sets[J]. Q J Math,1948,19(1)：193-199.

[2] COLES W, OLSON F. A note on complete residue systems[J]. Am Math Monthly,1954,61(9)：662-622.

[3] 孫琦，曠京華. 關于代數數域中的完全剩余系[J]. 數學學報,1987,30(2)：226-228.

[4] ATIYAH M, MACDONALD I. Introduction to commutative algebra[M]. New Jersey:Addison-Wesley,1969.

[5] BINI G, FLAMINI F. Finite commutative rings and their applications[M]. New York: Spring Science and Business Media,LLC,2002.

[6] 孫琦,萬大慶. 置換多項式及其應用[M]. 沈陽:遼寧教育出版社,1987.

[7] LIDL R, NIEDERREITER H. Finite Fields[M]. Encyclopedia Math Appl 20.Cambridge:Cambridge Univ Press,1997.

[8] COHEN S D. Permutation Group Theory and Permution Polynomials in Algebras and Combintorics[M]. Hong Kong:Springer-Verlag,1997.

[9] FRISCH S. Polynomial functions on finite commutative rings[M]. Lecture Notes in Pure and Appl Mathematics 205.New York:Dekker,1999.

[10] ZHANG Q. Polynomial functions and permutation polynomials over some finite commutative rings[J]. J Number Theory,2004,105(1):192-202.