平面向量常見典型考題賞析

■余智敏 何春玲

題型1：平面向量的基本概念

求解與平面向量的概念有關的命題的真假判定問題，關鍵在于理解平面向量的概念，還應注意零向量的特殊性以及兩個向量相等必須滿足:模相等且方向相同。向量與數(shù)量不同，數(shù)量可以比較大小，向量不能比較大小，但向量的模是非負實數(shù)，可以比較大小。

例 1給出下列四個命題:

①若|a|=|b|，則a=b；②若A，B，C，D是不共線的四點，則是四邊形ABCD為平行四邊形的等價條件；③若a=b，b=c，則a=c；④a=b 的等價條件是|a|=|b|且a∥b。

其中正確命題的序號是( )。

A.②③ B.①②

C.③④ D.①④

解：兩個向量的長度相等，但它們的方向不一定相同，①不正確。由，可得，又A，B，C，D是不共線的四點，可知四邊形ABCD為平行四邊形；反之，若四邊形ABCD為平行四邊形，則，②正確。由a=b，可得a，b的長度相等且方向相同，由b=c，可得b，c的長度相等且方向相同，所以a，c的長度相等且方向相同，即a=c，③正確。當a∥b且方向相反時，即使|a|=|b|，也不能得到a=b，故|a|=|b|且a∥b不是a=b的等價條件，④不正確。應選A。

跟蹤訓練1：給出下列四個命題:

①兩個具有公共終點的向量，一定是共線向量；②兩個向量不能比較大小，但它們的模能比較大小；③λ a=0(λ為實數(shù))，則λ必為零；④已知λ，μ為實數(shù)，若λ a=μb，則a與b共線。

其中錯誤的命題個數(shù)為( )。

A.1 B.2

C.3 D.4

提示：兩向量共線要看其方向而不是起點或終點，①錯誤。因為向量既有大小，又有方向，故它們不能比較大小，但它們的模均為非負實數(shù)，可以比較大小，②正確。當a=0時，不論λ為何值，λ a=0，③錯誤。當λ=μ=0時，λ a=μb=0，此時，a與b可以是任意向量，④錯誤。應選C。

題型2：共線向量定理及其應用

(1)利用共線向量定理可以證明向量共線，也可以由向量共線求參數(shù)的值。(2)若a，b不共線，則λ a+μb=0的等價條件是λ=μ=0，這一結論結合待定系數(shù)法應用非常廣泛。(3)證明三點共線的方法:若存在實數(shù)λ，使得，則A，B，C三點共線。

例 2設兩個非零向量a和b不共線。

(1)若3(a-b)，求證:A，B，D三點共線。

(2)試確定實數(shù)k的值，使k a+b與a+k b共線。

解：(1)因為=2a+8b，=2a+8b+3(a-b)=5(a+b)=5，由此可知共線。

又有公共點B，所以A，B，D三點共線。

(2)因為k a+b與a+k b共線，所以存在實數(shù)λ，使得k a+b=λ(a+k b)，即得解得k=±1。故當k=±1時，k a+b與a+k b共線。

跟蹤訓練2：已知a，b是兩個不共線的非零向量，且a與b起點相同。若a，t b，(a+b)這三個向量的終點在同一條直線上，則t=____。

題型3：平面向量基本定理的應用

平面向量基本定理表示向量的實質(zhì)是利用平行四邊形法則或三角形法則進行向量的加、減或數(shù)乘運算。利用平面向量基本定理解決向量問題的一般思路是:先選擇一組基底，并運用該基底將條件和結論表示成向量的形式，再通過向量的運算來解決問題。

例3如圖1，在△ABC中，設=a，=b，AP的中點為Q，BQ的中點為R，CR的中點恰為P，則=( )。

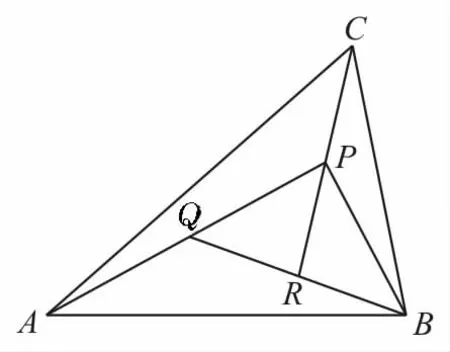
圖1

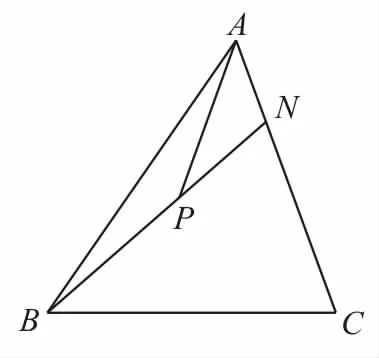
圖2

題型4：平面向量的數(shù)量積

向量數(shù)量積的兩種運算方法:①當已知向量的模和夾角時，可利用定義法求解，即a·b=|a||b|cos〈a，b〉；②當已知向量的坐標時，可利用坐標法求解，即若a=(x1，y1)，b=(x2，y2)，則a·b=x1x2+y1y2。

向量數(shù)量積的運算要注意兩點:①若a·b=a·c(a≠0)，則不一定得到b=c；②向量數(shù)量積的運算不滿足乘法結合律，即(a·b)·c不一定等于a·(b·c)。

例 4如圖3，在△ABC中，D是BC的中點，E，F(xiàn)是AD上的兩個三等分點，____。

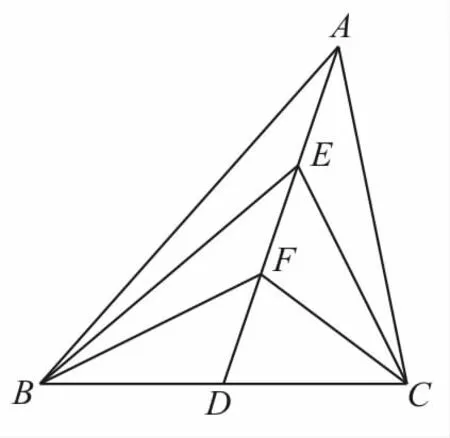
圖3

解：(方法1)以D為坐標原點，BC所在的直線為x軸，線段BC的中垂線為y軸，建立平面直角坐標系x Dy(圖略)。

跟蹤訓練4：如圖4，正方形ABCD的邊長為1，點E是AB邊上的動點，則的值為____，的最大值為____。

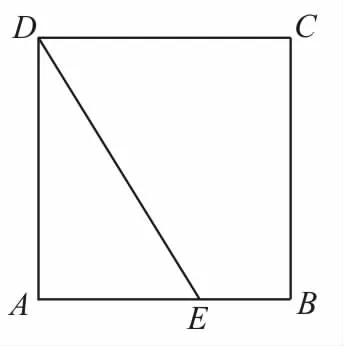
圖4

(方法2)以A為坐標原點，AB，AD分別為x軸，y軸，建立平面直角坐標系x Ay(如圖5)。

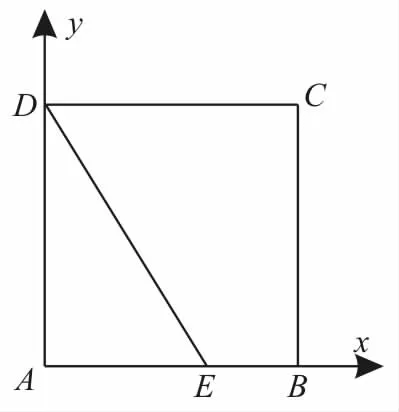
圖5

則 A(0，0)，B(1，0)，C(1，1)，D(0，1)。

設E(t，0)，t∈[0，1]，則=(t，-1)，=(0，-1)，可得=(t，-1)·(0，-1)=1。

由DC→=(1，0)，得=(t，-1)·(1，0)=t≤1，即的最大值為1。

(方法3)如圖6，無論點E在哪個位置，方向上的投影都是||=1，可得|·1=1。

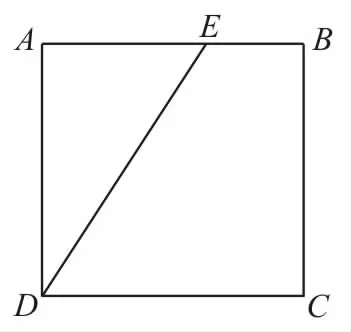
圖6

當點E運動到點B時，方向上的投影最大，其最大值為||=1，可得|·1=1。

題型5：平面向量的夾角

求向量的夾角的常見題型:①依據(jù)條件等式求兩向量的夾角，此類問題求解過程中應關注夾角的取值范圍；②依據(jù)已知圖形求兩向量的夾角，此類問題求解過程中應抓住“兩向量共起點”的特點。

求兩個非零向量的夾角要注意:①數(shù)量積大于0，說明不共線的兩個向量的夾角為銳角；②數(shù)量積等于0，說明兩個向量的夾角為直角；③數(shù)量積小于0且兩個向量不共線時，兩向量的夾角是鈍角。

例 5若向量a，b的夾角為，且|a|=2，|b|=1，則a與a+2b的夾角為( )。

解：設向量a與a+2b的夾角為α。

跟蹤訓練5：已知兩個單位向量a，b的夾角為60°，c=t a+(1-t)b。若b·c=0，則t=。

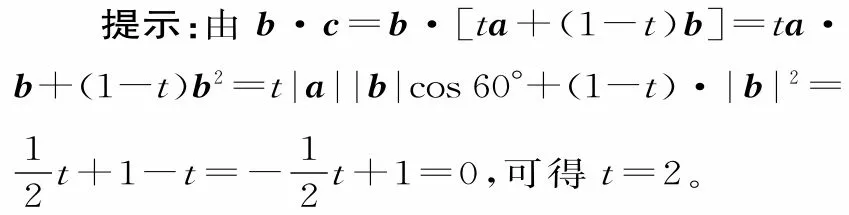
題型6：平面向量的模

把向量放在適當?shù)淖鴺讼抵校o有關向量賦予具體坐標求向量的模，如向量a=(x，y)，則|a|=。不把向量放在坐標系中，求向量的模，這時可利用公式|a|=及(a±b)2=|a|2±2a·b+|b|2轉(zhuǎn)化求解。

解：由題意可得|e1|=1，|e2|=1。由得〈e1，e2〉=60°。

由b·e1=b·e2=1＞0，可得〈b，e1〉=〈b，e2〉=30°。

由b·e1=1，可得|b||e1|cos 30°=1，故

題型7：平面向量的共線與垂直問題

平面向量的坐標表示可使平面向量的運算完全代數(shù)化，于是可利用“方程的思想”求解向量的共線與垂直問題。

跟蹤訓練7：已知向量a=(3，1)，b=(1，3)，c=(k，-2)，若(a-c)∥b，則向量a與c的夾角的余弦值是( )。

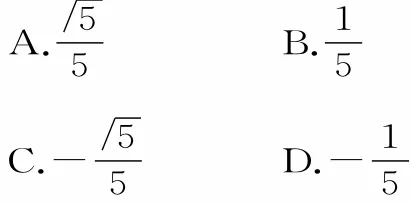
提示：由已知得a-c=(3-k，3)。

由(a-c)∥b，可得3(3-k)-3=0，解得k=2，這時c=(2，-2)。

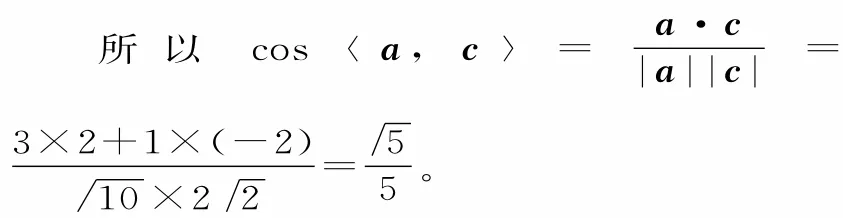
題型8：向量在解析幾何中的應用

向量在解析幾何中的作用:①載體作用，向量在解析幾何問題中出現(xiàn)，多用于“包裝”，解決此類問題的關鍵是利用向量的意義、運算，脫去“向量外衣”。②工具作用，利用a⊥b?a·b=0，a∥b?a=λ b(b≠0)，可解決垂直、平行問題。

例8(1)已知向量(4，5)，=(10，k)，且A，B，C三點共線，當k＜0時，若k為直線的斜率，則過點(2，-1)的直線方程為____。

(2)設O為坐標原點，C為圓(x-2)2+y2=3的圓心，且圓上有一點M(x，y)滿足=____。

解：(1)由=(4-k，-7)，=(6，k-5)，且，可得(4-k)(k-5)+6×7=0，解得k=-2或k=11。

由k＜0，可知k=-2，則過點(2，-1)且斜率為-2的直線方程為y+1=-2(x-2)，即2x+y-3=0。

(2)由=0，可得OM⊥CM，可知OM是圓的切線。

設OM的方程為y=k x。

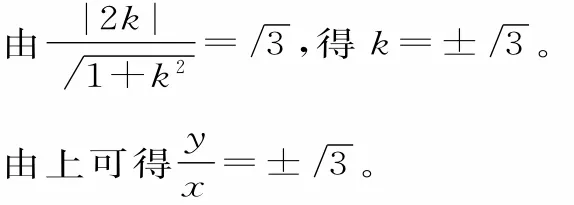
跟蹤訓練8：已知圓C:(x-2)2+y2=4，圓M:(x-2-5cosθ)2+(y-5sinθ)2=1(θ∈R)，過圓M 上任一點P作圓C的兩條切線P E，P F，切點分別為E，F(xiàn)，則P→E·P→F的最小值是( )。

A.5 B.6

C.10 D.12

提示：由圓C:(x-2)2+y2=4，可知圓心C(2，0)，半徑為2。

由圓M:(x-2-5cosθ)2+(y-5sinθ)2=1，可知圓心 M(2+5cosθ，5sinθ)，半徑為1。由于CM==5＞2+1，所以圓C與圓M相離。

如圖7所示，設直線CM 和圓M 交于H，G兩點，則的最小值是。

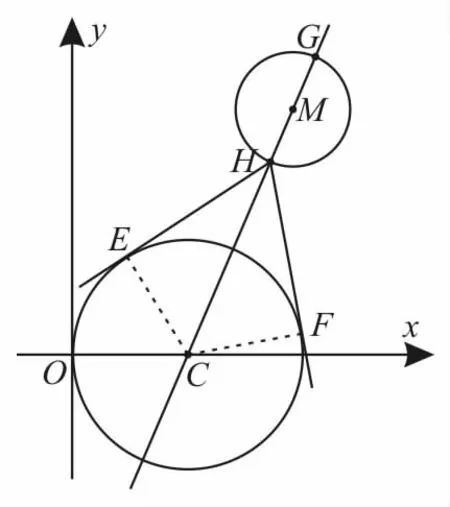
圖7

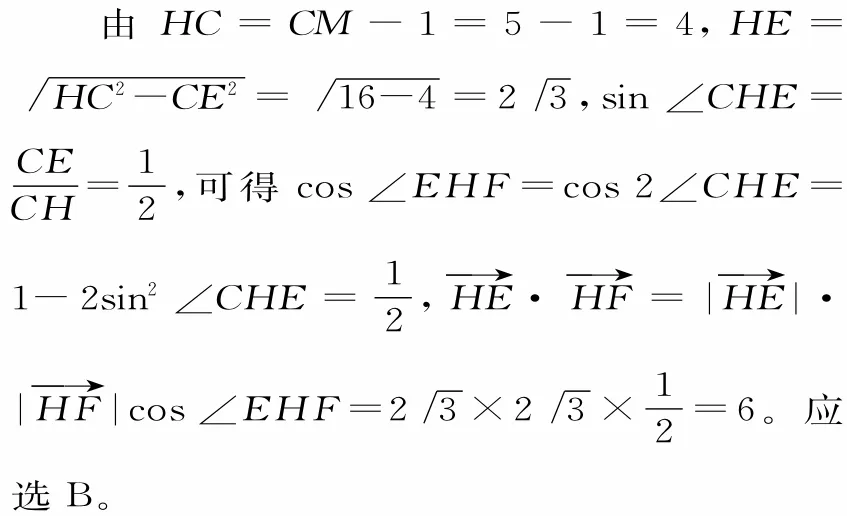
題型9：平面向量與三角函數(shù)的交匯問題

平面向量與三角函數(shù)的交匯問題是近幾年高考的熱點，應該引起同學們的重視。

(1)若m⊥n，求tanx的值。

提示：由題意可知6sin2α+cosα(5sinα-4cosα)=0，即 6sin2α+5sinαcosα-4cos2α=0。

上述等式兩邊同除以cos2α，得6tan2α+5tanα-4=0。

題型10：平面向量中的新定義問題

這類問題的特點是背景新穎，信息量大，通過它可考查同學們獲取信息，利用信息分析和解決問題的能力。解答這類問題，首先要分析新定義的特點，把新定義所敘述的問題的本質(zhì)弄清楚，然后應用到具體的解題過程中，這是破解新定義信息問題難點的關鍵。

例10對任意兩個非零的平面向量α向量a，b滿足a與b的夾角b等于( )。

跟蹤訓練10：設向量a=(a1，a2)，b=(b1，b2)，定義一種向量積a?b=(a1b1，P(x，y)在y=sinx的圖像上運動，Q是函數(shù)y=f(x)圖像上的點，且滿足=m?+n(其中O為坐標原點)，則函數(shù)y=f(x)的值域是____。

提示：設點Q(c，d)。

由點P(x，y)在y=sinx的圖像上，可知點P(x，sinx)。