基于SAHDE-RVM的鐵路短期風速預測研究
楊溪源,李彥哲
(蘭州交通大學自動化與電氣工程學院, 蘭州 730070)
近年來,我國鐵路事業迅猛發展,隨著列車運行速度的不斷提高,鐵路運營安全成為人們關注的熱點。鐵路運營安全主要包括:列車車體安全、信號與通信系統安全、調度指揮安全等[1-2]。其中,脫軌作為列車車體安全考慮因素之一,容易受大風等自然災害的影響[3-4]。在大風環境及風口區域的高路堤、丘陵等特殊路段中,由于列車氣動性能惡化,導致列車穩定性受到嚴重影響,大大增加列車脫軌的可能性[5],因此,對鐵路風速預測研究,顯得尤為重要。
國外,文獻[6-7]提出在鐵路沿線建立擋風墻、列車外形優化等的方法,一定程度上解決了大風對高速列車運行的影響,但是有一定的局限性;文獻[8]根據列車運行沿線歷史風速數據以實現外推估計的風速預測研究,該方法簡單、實時性好,但預測精度不高;國內,文獻[9-11]針對鐵路沿線風速短期預測,學者分別利用時間序列分析理論和神經網絡等方法進行預測研究,很好的提高了風速預測精度,但存在神經網絡初始權值和選擇訓練數據樣本不易確定等缺陷,基于此,支持向量機法等機器學習型算法應運而生,以結構風險最小化為目標的SVM預測模型較神經網絡模型具有較高的精度,這在一定程度上克服了神經網絡在鐵路短期風速預測中的劣勢[12],但是SVM模型仍存在核函數選擇條件苛刻需遵循Mercer條件,核函數較多且其值的選取對SVM模型的預測精度有著較大的影響。在此,本文根據新型計算機算法相關向量機核函數選擇靈活無需遵循Mercer條件,核參數的設置數目少的特點,利用差分進化算法在參數優化方面的優勢,采用交叉算子可自適應調整的自適應差分進化算法,并混合了模擬退火算法對最優參數進行二次優化,提出了基于自適應混合差分進化相關向量機(Self-Adaptive Hybrid Differential Evolution-Relevance Vector Machine, SAHDE-RVM)的鐵路短期風速預測模型,通過實例對預測模型進行驗證,并與現有模型的預測結果進行對比分析。
1 相關向量機原理
相關向量機(Relevance Vector Machine, RVM)是一種基于貝葉斯框架的算法[13]。與傳統的SVM相比,RVM具有高稀疏性,僅有核參數的設置,核函數的選擇靈活,無需滿足Mercer條件等優點,在回歸預測方面有著良好的應用價值。
本文使用RVM進行回歸預測,建立RVM回歸預測模型。給定訓練樣本的輸入集X={x1,x2,x3,…,xn,}與相應的輸出集T={t1,t2,t3,…,tn},其中n為樣本個數,設ti為目標值且有ti∈R。輸出值ti的函數模型可表示為
ti=y(xi,w)+εi
(1)
式中,εi表示高斯白色噪聲,且εi服從分布εi~N(0,σ2),則p(ti|xi)=N(ti|y(xi,w),σ2)。RVM模型的輸出可表示為非線核函數的組合,核函數無需滿足mercer條件。RVM的回歸預測模型為
(2)
式中,wi為加權系數;K(x,xi)為核函數;N為樣本數量。
對于獨立分布的輸出集ti的似然估計為
(3)
式中,Φ=(Φ1,Φ2,…,ΦN);Φi=(1,K(xi,x1),…;K(xi,xn))T(i=1,…,N)。
由稀疏貝葉斯原理定義的權值參數為零的高斯先驗分布為
(4)
式中,αi為先驗高斯分布的超參數;α=(α0,…,αN)T。每個獨立的超參數αi控制著權參數wi的先驗分布,使相關向量機模型具有稀疏性。
由式(3)、式(4)根據貝葉斯原理計算權值矢量w的后驗分布
N(w|μ,∑)
(5)
式中,μ=σ-2∑φTt,∑=(A+σ-2φTφ)-1,A=diag(α0,α1,…,αN)。
由式(5)可知,若要確定權值矢量w需對超參數α、σ2進行確定。用貝葉斯框架計算超參數的似然分布
(6)
式中,C為協方差且C=σ2I+ΦA-1ΦT。
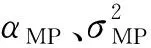
(7)
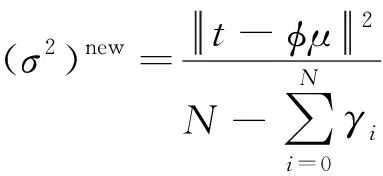
(8)
式中,uj是第j個后驗平均權值;γj=1-αjMjj(γj∈[0,1]);Mjj為權值協方差矩陣Σ的對角線元素。
RVM學習過程中,首先初始化式(7)、式(8)中的兩個參數,并通過更新迭代公式不斷更新計算兩個超參數,當模型中的參數均達到最大訓練次數時,更新計算停止,此時得到的α與σ2為最優值。若給定系統一個輸入值X*,則輸出的概率分布為
N(t)(t*|y*,σ2)
(9)
y*=uTΦ(X*)=uMPΦ(X*)
(10)
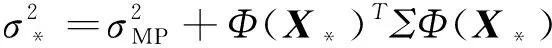
(11)
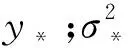
2 自適應混合差分進化算法
2.1 差分進化算法
Storn R和Price K于1995年提出了差分進化算法(Differential Evolution,DE),DE是一種使用實數矢量編碼的群體智能化的優化算法,其原理類似于遺傳算法。DE具有強大的易用性、魯棒性和全局搜索能力,已有大量的文獻證明DE算法的優越性高于遺傳算法、蟻群算法等智能算法[14]。DE通過對群體中的個體分別進行變異、交叉、選擇等操作獲取最優個體,從而得到最優值。但DE算法仍然具有易早熟,較難搜索到全局最優解等缺陷,鑒于此,本文采用一種自適應混合差分進化算法(Self-Adaptive Hybrid Differential Evolution,SAHDE)[15-17],該模型可自適應調整DE的交叉概率算子CR,在算法的初期保持種群的多樣性的同時提高其全局搜索能力,并引入了模擬退火算法,該算法具有較強的搜索能力可對獲取的最優解進行二次搜索,SAHDE算法可解決DE算法早熟收斂,優化算法的全局所搜能力。差分進化算法的操作步驟如下。
(1)變異操作:DE算法由多種變異操作方法,本文選用如下方法進行變異操作。
xm=xbest+F[(x1-x2)+(x3-x4)]
(12)
隨機挑選出4個父代個體,分別記為x1,x2,x3,x4;xbest是父代中的最優個體;xm為變異產生的變異個體;F為變異率(F∈[0,1.2])。
(2)交叉操作:選取兩個個體xi和xm進行交叉操作,交叉操作后生成的新個體為xc,具體的操作方法如下式
j=1,2,…,D
(13)
其中,rand()表示[0,1]之間的隨機函數,randr(i)∈{1,2,…,D}為隨機產生的整數;D為優化變量的維數;CR為交叉率(CR∈(0,1))。
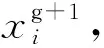
(14)
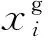
2.2 交叉算子的自適應調整
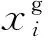
(15)
CR0為交叉算子CR的初值,CR的值根據上式自適應調整,初始值CR0較小,而后其取值逐步增大,此時算法具備一個優秀搜索算法所具備的能力,與傳統DE相比具有更好的性能。
2.3 模擬退火算法的引入
DE種群的多樣性會導致其早熟收斂。為了進一步提高算法的搜索效率,本文使用模擬退火算法對SAHDE產生的當前最優個體進行二次搜索。在SAHDE當中,選定當前最優個體為初始個體,既y0=xbest初始溫度選定為T0,產生新個體的方式如下所示
yr+1,j=yr,j+ηε(xjmax-xjmin)
j=1,2,…,D
(16)
式中,r為模擬退火算法的迭代次數;yr為r次迭代后產生的新個體;η為控制擾動幅度;ε為服從均值或正態分布的隨機變量;xjmax、xjmin分別為第j維優化變量的取值范圍。
SAHDE產生的最優個體再經過模擬退火算法二次搜索后,適應度變化為ΔF,ΔF=f(yr+1)-f(yr)。若ΔF<0則接受新個體并用新個體替換原來的最優個體;若e(-ΔF/T)>rand(),此時也接受新產生的個體,并用其替換種群中的一個非最優個體;否則拒絕。若選擇了接受新的個體,按Tr+1=aTr(0 為了加快樣本的訓練速度并提高模型的預測精度,本文使用均值化的方法對風速實測樣本數據進行預處理 (17) 核函數是RVM技術的核心,核函數的使用有效地解決了數據空間、特征空間、類別空間之間的非線性變換。傳統的RVM選取的單一核函數具有其自身的局限性,本文采用混合核函數,將不同的核函數進行組合,取長補短,發揮各自的優勢,組合后的核函數具有優秀的性能。 通過參考文獻[18]對不同核函數性能的對比研究,本文選用高斯核函數與二項式核函數組合得到的組合核函數作為RVM模型的核函數。組合后的核函數如下 K(xi,xj)=λG(xi,xj)+(1-λ)P(xi,xj) (18) 通過對樣本數據集的訓練,自適應獲取模型的最優參數α、σ2。 RVM模型核參數的選取對模型回歸預測的結果起關鍵作用,為減小人為參數設置不當而引起的較大預測偏差,本文SAHDE的適應度函數以文獻[19]的留一交叉驗證法得到,進而RVM模型的參數可自適應獲取。基于此,提出SAHDE-RVM模型,RVM參數可自適應獲取最優值,從而減小了人為參數設置不當而產生的預測誤差。具體步驟如下。 (1)為選取RVM的最優參數,首先以差分進化算法的個體維數等于需要確定的RVM參數的個數進行實數編碼。 (2)對SAHDE參數初始化,種群規模設置為100且采用實數編碼,變異率F=0.35,初始交叉率CR0=0.4,最大進化代數gmax=1 800;以群體特征信心確定模擬退火算法的初溫,模擬退火算法的迭代次數為100,即第100次迭代后最優個體保持不變則停止操作。 (3)用適應度函數來評價種群中的個體,判斷其是否達到最優,以此選取此步驟所確定的最優個體。 (4)上一步驟得到最優個體之后,采用模擬退火算法對已確定的最優個體進行二次搜索。 (5)根據公式(15)計算當代交叉率CR后更新SA參數。 (6)判斷是否滿足終止條件,既達到最大進化數量,若滿足條件,此時確定了RVM的最優參數,以此參數建立RVM回歸預測模型;若未達到終止條件,返回步驟(3)繼續執行直至滿足條件為止。 模型預測流程如圖1所示。 圖1 SAHDE-RVM模型預測流程 合理的誤差分析能對所使用的方法進行恰當的評判。本文選取均方根誤差RMSE和平均相對誤差MAPE作為模型誤差的評價指標,其表達式如下 (19) (20) 本文采用我國海南東環鐵路及青藏鐵路某監控點2012年11月2日至2012年11月29日之間的實測風速數據,設置原始數據的采樣間隔均為15 min,經數據預處理后分別得到各1 300組數據,利用前1000組數據作為訓練樣本,后300組數據進行測試。將相同的數據樣本分別利用本文所提出的SAHDE-RVM模型、最小二乘支持向量機(Least Squares-Support Vector Machine, LS-SVM)模型和傳統DE參數尋優的RVM模型進行預測,并對比分析。其中,LS-SVM模型采用文獻[20]所提出的EEMD-LSSVM模型,首先對實測的風速序列進行總體經驗模態分解,由風速的不同趨勢將風速序列分解為各個子序列,對每個子序列分別建立LSSVM模型,最終疊加各個子序列的預測結果,其參數優化方法采用自適應擾動粒子群算法進行優化,選取其最優值。RVM模型的參數采用傳統的DE進行參數尋優。SAHDE-RVM的參數采用本文所提出的自適應混合差分進化算法(SAHDE)尋優得到其最優值。海南東環鐵路記為A段,提前15 min及30 min短期風速預測結果如圖2所示;青藏鐵路記為B段提前15 min及30 min短期風速預測結果如圖3所示。 圖2 A段鐵路短期風速預測 圖3 B段鐵路短期風速預測 由圖2、圖3可知,在風速預測模型中,數據相同的情況下,SAHDE-RVM模型、LS-SVM模型和傳統的RVM模型對風速進行預測都具有一定的精度,A段不同方法在測試集上提前15、30 min預測的結果如表1所示。 表1 A段鐵路不同方法的預測性能 B段不同方法在測試集上提前15、30 min預測的結果如表2所示。 表2 B段不同方法的預測性能 由表1、表2可以看出,一方面本文所提出的SAHDE-RVM模型預測結果與真實數據較為接近,A段、B段鐵路提前15 min均方根誤差RMSE僅有1.218 6%和1.318 2%,同時兩段鐵路的平均相對誤差MAPE均高于鐵路現場精度15%的要求;另一方面在給定樣本條件下,SAHDE-RVM模型預測結果的平均相對誤差MAPE較LS-SVM模型明顯減小,且小于傳統DE參數尋優的RVM回歸預測模型,同樣地,SAHDE-RVM模型的均方根誤差eRMSE值小于LS-SVM、RVM。由此可見,本文所提出的使用SAHDE進行RVM參數尋優的SAHDE-RVM預測模型有一定的正確性,且較傳統模型精度有了較大提升,具有較高的回歸預測精度。 (1)針對鐵路沿線短期風速預測,本文提出采用一種基于自適應混合差分進化相關向量機模型對鐵路沿線短期風速進行預測,以國內兩段鐵路沿線實測風速數據為依據,將本文方法預測結果與實際風速數據對比分析得出,SAHDE-RVM模型的預測結果與實際數據之間具有良好的相似性,從而驗證了本文所構建SAHDE-RVM風速預測模型的準確性。 (2)以同一實測風速數據為樣本,分別采用SAHDE-RVM、LS-SVM、DE-RVM進行預測,對比得出:SAHDE-RVM模型既克服了傳統神經網絡預測法泛化能力差訓練時間長且易陷入局部最小值的缺點,又解決了支持向量機核函數選取不靈活,需要遵循Mercer條件的缺陷,降低了傳統方法由于核函數參數設置不當而引起的模型精度誤差,具有較高的精度,有良好的工程應用價值。 [1] Grnbak J, Madsen T K, Schwefel H P. Safe wireless communication solution for Driver Machine Interface for train control systems[J]. 3rd International Conference on Systems, 2008:208-213. [2] Blakstad H C, Hovden Jan, Rosness R. Reverse invention: An inductive bottom-up strategy for safety rule development A case study of safety rule modifications in the Norwegian railway system[J]. Safety Science, 2010,48(3):382-394. [3] 田紅旗.中國列車空氣動力學研究進展[J].交通運輸工程學報,2006,6(1):1-9. [4] Liu Hui, Tian Hongqi, Li Yanfei. Short-term forecasting optimization algorithms for wind speed along Qinghai-Tibet Railway based on different intelligent modeling theories[J]. Journal of Central South University of Technology(English Edition), 2009,16(4):690-696. [5] 劉輝.鐵路沿線風信號智能預測算法研究[D].長沙:中南大學,2011:1-12. [6] Chu C R, Chang C Y, Huang C J, et al. Windbreak Protection for Road Vehicles Against Crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamic, 2013,116(5):61-69. [7] Simonovic A, Svorcan J, Stupar S. Aerodynamic Characteristics of High Speed Train under Turbulent Cross Wind: A Numerical Investigation Using Unsteady-RANS Method[J]. FME Transactions, 2014,42(1):10-18. [8] Hppmann U, Koenig S, Tielkes T, et al. A short-term strong wind prediction model for railway application: design and verification[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002,90(10):1127-1134. [9] 潘迪夫,劉輝,李燕飛,等.青藏鐵路格拉段沿線風速短時預測方法[J].中國鐵道科學,2009,29(5):129-133. [10] 劉輝,潘迪夫,李燕飛.基于列車運行安全的青藏鐵路大風預測優化模型與算法[J].武漢理工大學學報(交通科學與工程版),2008,32(6):986-989. [11] 劉輝,田紅旗,等基于小波分析法與神經網絡法的非平穩風速號短期預測優化算法[J].中南大學學報(自然科學版),2011,42(9):2704-2711. [12] 劉蘇蘇,孫立民.支持向量機與RBF神經網絡回歸性能比較研究[J].計算機工程與設計,2011,32(12):4202-4205. [13] 馬開良.基于相關向量機的復合模型在風速預測中的研究及應用[D].蘭州:蘭州大學,2014:10-14. [14] Price K, Storn R, Lampinen J. Differential evolution: A practical approach to global optimization[M]. Berlin Heidelberg:Springer, 2005:1-29. [15] 胡玉純.自適應差分進化算法在PMSM電機控制器中的應用[D].鄭州:鄭州大學,2014,23-38. [16] 沈佳杰,江紅,王肅.基于自適應縮放比例因子的差分進化算法[J].計算機工程與設計,2014,35(1):261-266. [17] 燕飛,秦世引.一種基于模擬退火的支持向量機超參數優化算法[J].航天控制,2008,26(5):7-11. [18] 樓俊鋼,蔣云良,申情,等.軟件可靠性預測中不同核函數的預測能力評估[J].計算機學報,2013,36(6):1303-1311. [19] 劉學藝,李平,郜傳厚.極限學習機的快速留一交叉驗證算法[J].上海交通大學學報,2011,45(8):1140-1146. [20] 王賀,胡志堅,張翌暉,等.基于聚類經驗模態分解和最小二乘支持向量機的短期風速組合預測[J].電工技術學報,2014,29(4):237-245.3 自適應混合差分進化相關向量機模型的構造
3.1 樣本數據的預處理
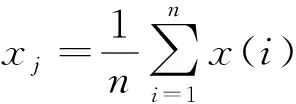
3.2 RVM模型核函數的選取
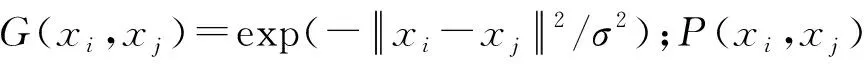
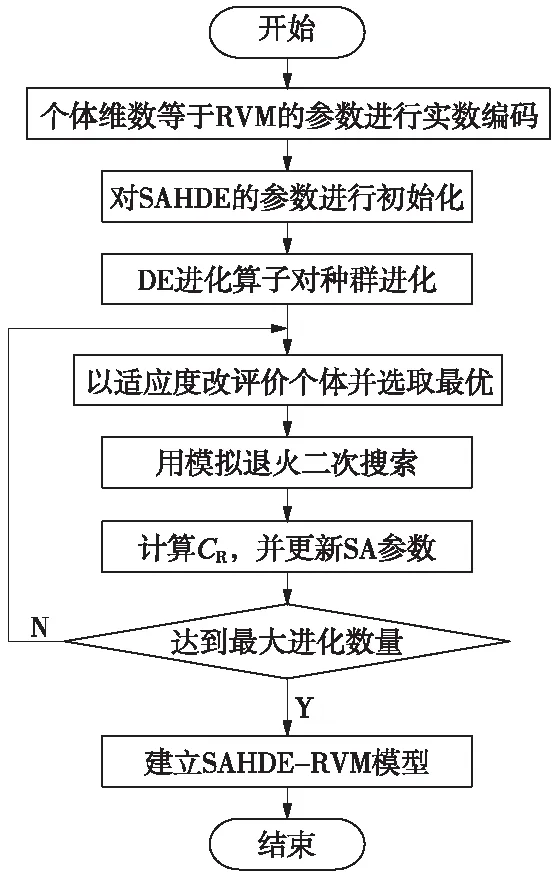
3.3 自適應混合差分進化相關向量機模型流程
3.4 模型精度評價指標
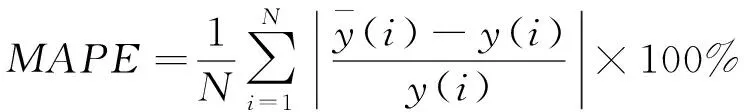
4 算例分析
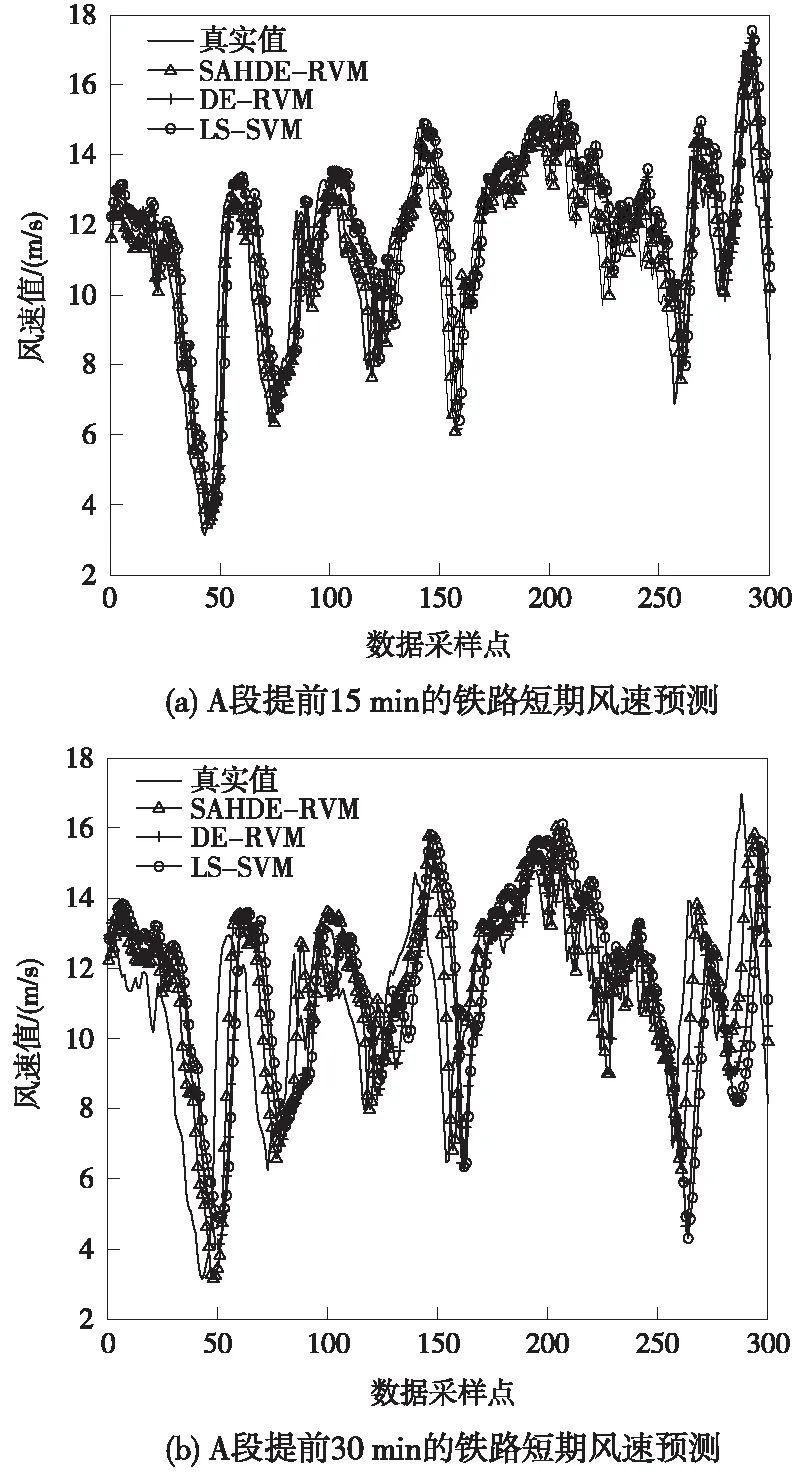
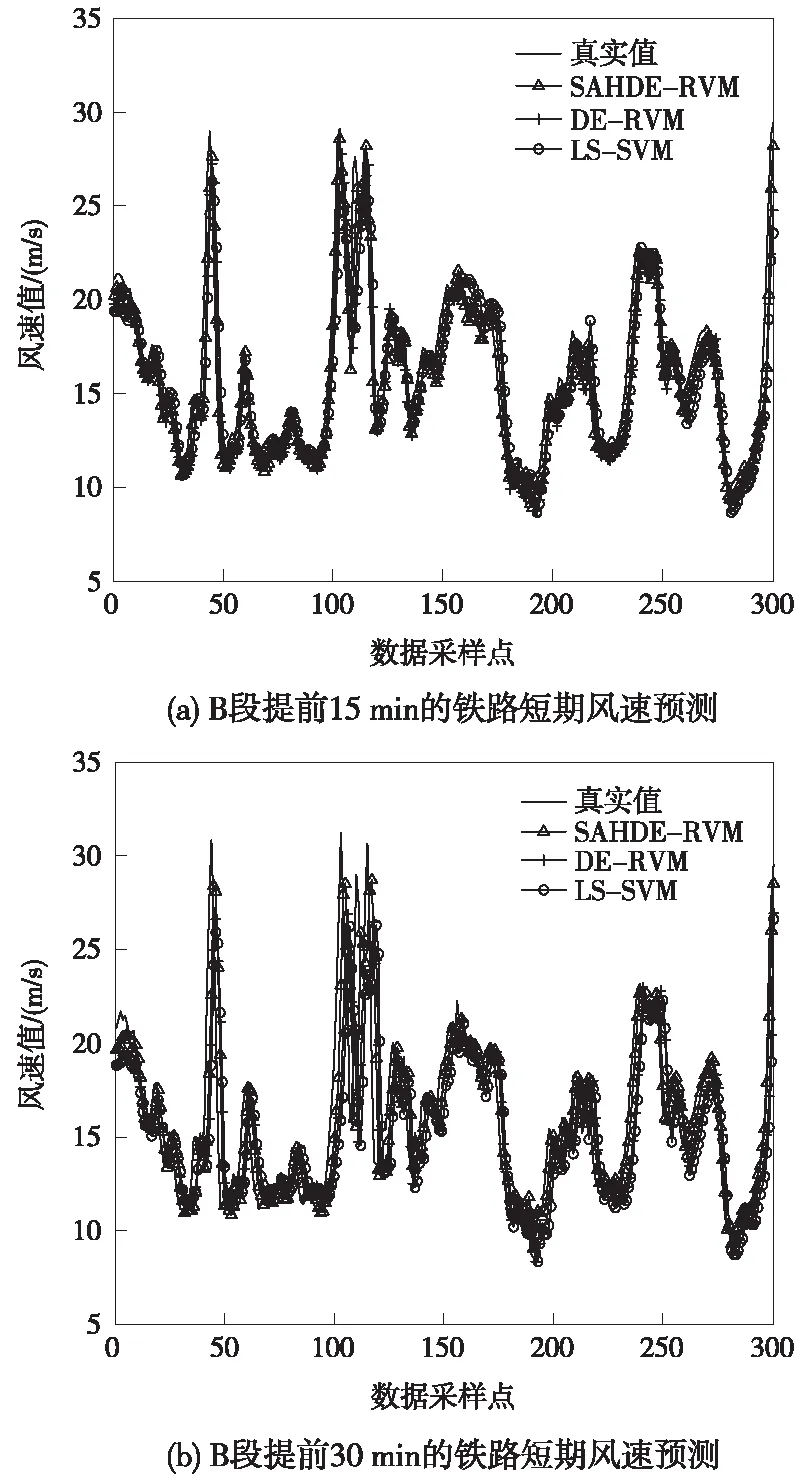
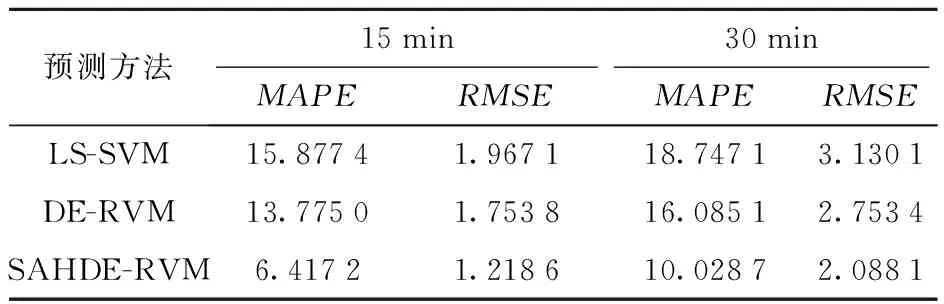
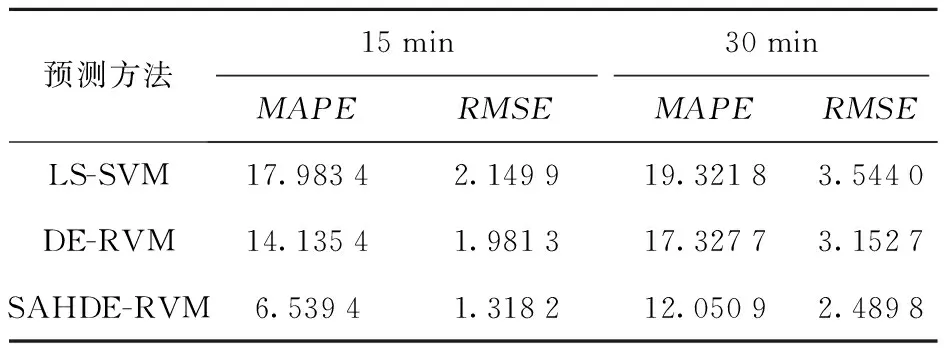
5 結論

