基于混合多屬性決策的鐵路站位方案評價模型

羅 圓,朱 穎,張小強,姚令侃

(1.中鐵二院工程集團有限責任公司,成都 610031； 2.西南交通大學土木工程學院,成都 610031)

鐵路選線時車站位置的分布和站址的選擇往往影響線路的局部走向，它關系到城市規劃、工程投資、運營收入，甚至是周邊地區經濟發展等一系列主要問題，是一個多層次、多因素、多指標的多目標決策過程[1]。鐵路車站的選址和建設，因其牽涉面廣、問題復雜、取決因素多而情況各異，故難以找到普遍性的規律，使得目前理論依據及定量方法技術缺乏[2，3]。如果部分車站選址不合理，將降低旅客出行和貨物運輸效率，甚至導致生態環境和社會等多方面的問題。

傳統的鐵路選線方案評價和比選，主要是在經濟上追求換算工程運營費最省，并對比較方案的工程技術條件、環境影響、社會效益等定性因素進行分析，選出最優方案[4-9]。這種方法在很大程度上要依靠專家的工程實踐經驗，不僅增加了專家的工作量，而且容易受主觀因素的影響。同時，當定量指標和定性指標相互交叉，難以直接確定最優方案時，目前也缺乏相應的綜合評價方法。基于此，本文根據鐵路選線設計的特點，遵循站位方案比選原則，建立全面的評價指標體系；引入離差最大法計算指標的權重，然后利用三角模糊數對定性指標進行量化；最后使用混合多屬性決策方法解決鐵路站位方案的定量和定性綜合評價和比選問題，進而確定最優站位方案，為實際決策者提供定量化的決策支持和確實可行的依據。

1 鐵路站位方案綜合評價指標體系

鐵路站位方案評價和比選是一個復雜的系統工程，首先需要解決的技術關鍵是提出方案評價指標，以構建評價指標體系，但由于該方面理論仍處于探索階段，目前還沒有統一的構建標準。通過現場調研和向專家咨詢，利用層次分析法的原理，從技術、經濟、環境和社會4個宏觀層面，選擇了橋隧比、工程投資、對生態環境的影響和滿足地方需求的能力等定量、定性相結合的指標，建立了如表1所示的鐵路站位方案綜合評價指標體系，可依據鐵路決策設計時站位方案的實際情況作相應選擇和調整。

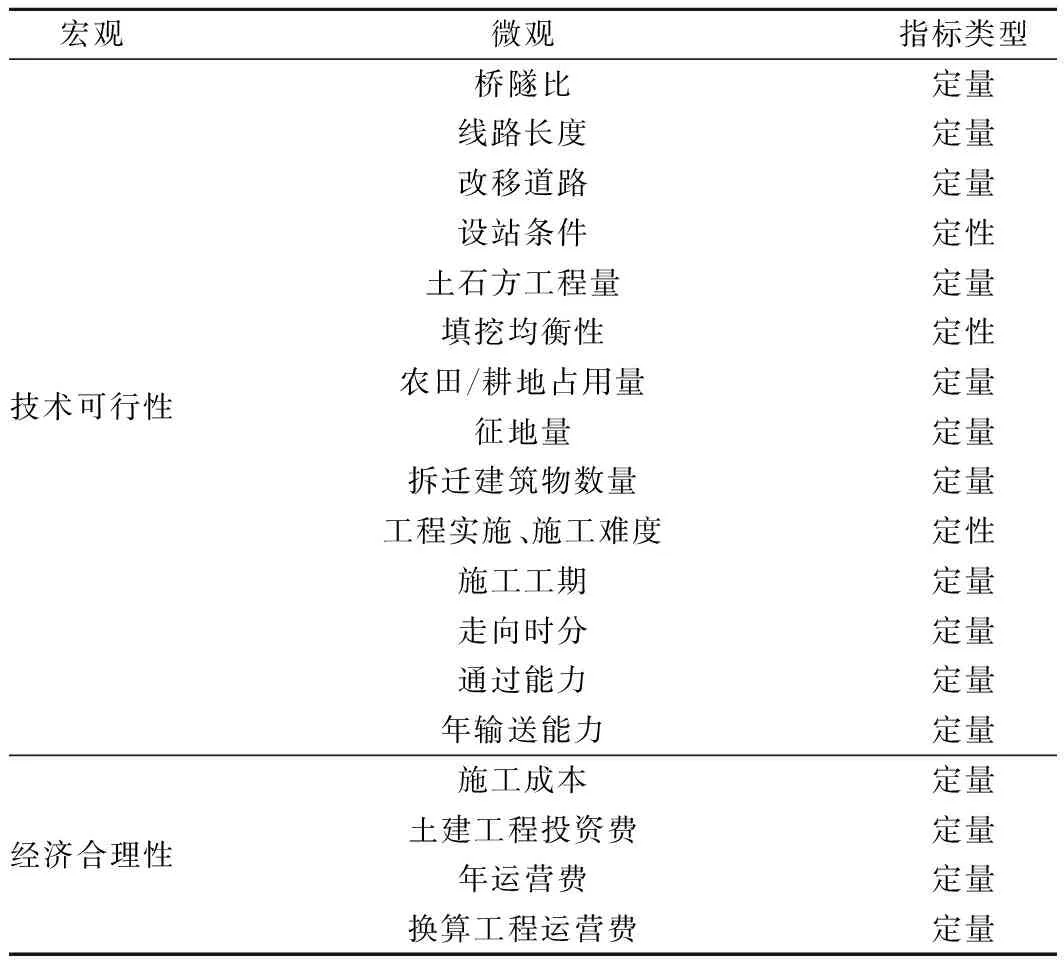
表1 鐵路站位方案綜合評價指標體系

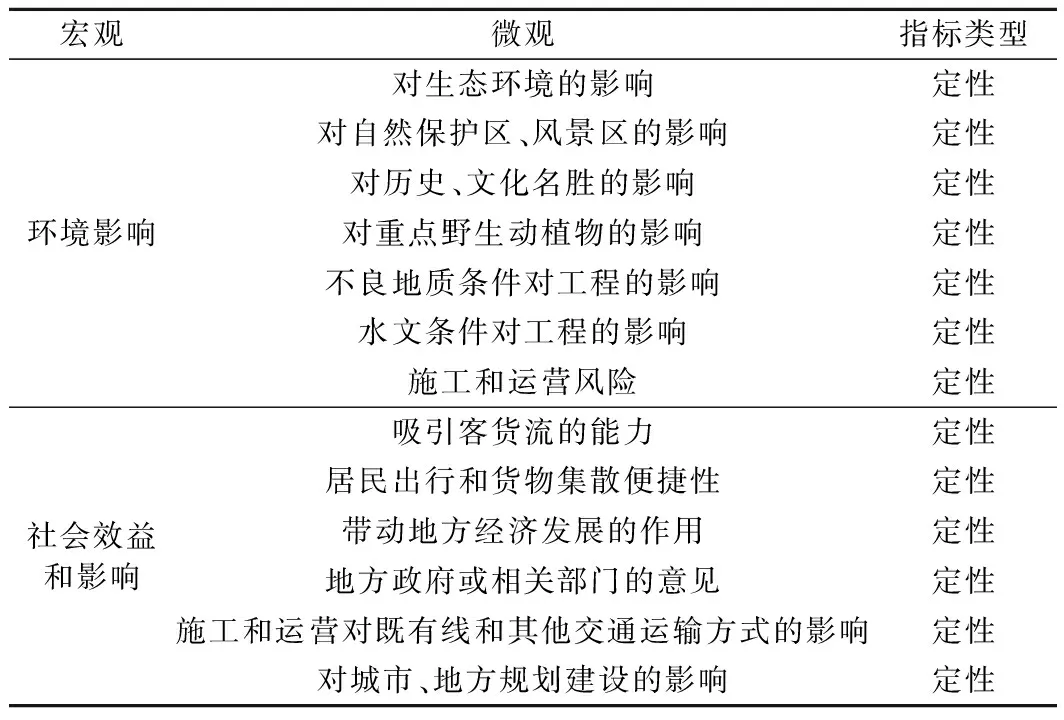
續表1

2 基于離差最大化的指標權重確定

目前，鐵路選線設計的方案比選中廣泛采用層次分析法(AHP)，但其計算比較復雜，且需要由專家對指標之間進行相互比較和賦值，當評價指標較多時會成指數倍增加專家的工作量，且計算的指標權重易受專家主觀因素的影響。為此，引入離差最大化方法，計算指標的權重。該方法只利用指標取值的差異程度來確定權重，方法原理清晰，計算簡單，且避免了主觀因素的干擾，能給決策者以最客觀的決策支持。

離差最大化法計算指標權重的基本原理為：如果某個指標在所有方案下取值的差異(或距離)越大，則表明該指標對方案比選所產生的影響就越大，那么決策者就應該更加重視該指標，其權重就越大；反之，則表明該指標對方案比選所產生的影響就越小，其權重也相應的就越小。因此，從指標實際取值情況對方案比選能夠產生的影響程度方面考慮，不管指標本身在決策者心目中的重要性如何，哪個指標取值的差異程度(即離差)越大，它就應該被賦予越大的權重；而離差越小權重就越小[10-11]。

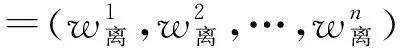
首先，用Dij(W)表示方案Xi與其他方案關于指標Cj取值的偏差，則可定義

并且設

對指標Cj而言，Dj(W)表示所有方案與其他方案的偏差，而指標權重向量W的選擇應該使所有指標對所有方案的總偏差最大。所以構造偏差函數

(1)

故，通過求解下面單目標最優化問題就可以求出指標的權重向量W

(2)

通過構造下面的拉格朗日函數，求解式(2)中的最優化問題

分別對wj和δ求偏導，并令其為0，得到

(3)

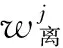
(4)

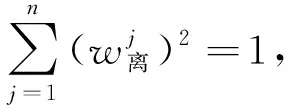
(5)

將式(5)代入式(4)中，并進行歸一化處理后得到

(6)

3 基于混合多屬性決策的鐵路站位方案綜合評價模型

3.1 混合多屬性決策

在多屬性決策問題中，由于屬性有定性和定量之分，決策方案在各指標下的取值有3種情況：全部為定量值，即數字；全部為定性描述，即語言；其數據可以是精確的，也可以是不精確的，如區間數，模糊數等；既有定量值又有定性描述。與這3種情況對應的多屬性決策問題分別稱為定量型、定性型和混合型多屬性決策問題。為了保持定性指標取值信息的模糊性，本文利用三角模糊數對定性指標進行量化，因此，定性指標量化的三角模糊數和定量指標取值的精確實數一起，構成了一個混合多屬性決策問題。本文利用混合多屬性理論中的TOPSIS原理[12-13]，構建鐵路站位方案評價和比選模型。

3.2 鐵路站位方案評價模型

3.2.1 三角模糊數

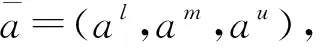
(7)

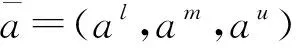
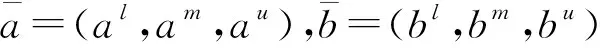
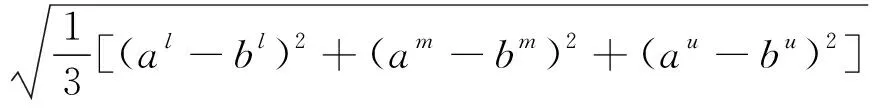
(8)

3.2.2 方案綜合評價和比選步驟

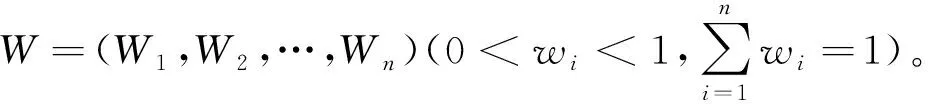
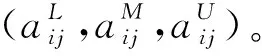
表2 語言類模糊數與三角模糊數的轉化關系

傳統的鐵路方案評價方法主要采用專家打分，使用1、3、5、7等確定的數對定性指標進行量化[15]，這種處理方法對指標的模糊性等不確定性特征考慮不足。因此，本文利用三角模糊數對定性指標進行量化，這樣就能充分考慮到定性指標量化后的模糊性，使得最后的綜合評價結果更接近于實際情況。

將定量指標取值的實數和定性指標取值量化后的三角模糊數進行組合，構成站位方案綜合評價和比選的決策矩陣A=(aij)mXn。

(2)分別利用式(9)、式(10)和式(11)、式(12)對定量指標取值的實數和定性指標取值的三角模糊數進行規范化處理，得到規范化矩陣S=(sij)mXn。

①對于定量指標取值為精確數時，對于效益型指標，規范化方法為

(9)

對于成本型指標，規范化方法為

(10)

②當定性指標取值為三角模糊數時，對于效益型指標，規范化方法為

(11)

對于成本型指標，規范化方法為

(12)

(3)利用式(6)計算指標的權重W。然后利用權重W對規范化矩陣S進行加權，得到加權規范化矩陣Y=(yij)mXn，其中yij=wj×sij，i=1，2，…，m，j=1，2，…，n。

(4)利用混合TOPSIS法原理，確定方案評價值并進行方案排序。

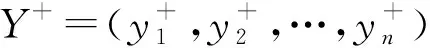
a.對于定量指標指標

(13)

b.對于定性指標

j=k+1,…,n;

(14)

j=k+1,…,n

(15)

②計算各備選方案到正理想方案與負理想方案的距離。

第i個方案到正理想解Y+的距離為

(16)

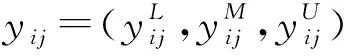
第i個方案到負理想解Y-的距離為

(17)

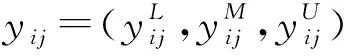
③計算各方案的綜合相對貼近度

(18)

顯然綜合相對貼近度Pi的值介于0～1。當Pi=1時，站位方案綜合評價值最高；當Pi=0時，站位方案綜合評價值最低。

(5)根據Pi值的大小對方案進行排序：Pi值越大，則方案整體評價值越大，表明方案Xi越優；Pi值越小，則方案整體評價值越小，表明方案Xi越差。

4 實例分析

結合云桂鐵路廣南站位方案研究，進行方案評價和比選實例分析。云桂線位于廣西和云南范圍內，線路長714.559 km。廣南縣位于云南省東南部，文山州東北部，滇、貴、黔三省(區)交界處。廣南縣人口76萬人，居云南省第6位，經濟發展水平遠低于全國、全省平均水平，是國家扶貧開發工作重點縣和云南省重點扶持的人口大縣；廣南縣境內自然資源豐富，有八寶貢米、生態油茶等生物資源，礦產、水能資源也非常豐富，有全國第二大銻礦企業木利銻業，可開發水能資源31.9萬kW；境內自然環境優美，歷史底蘊深厚，民族文化多姿多彩，“世外桃源”壩美景區、省級風景名勝區八寶和省級歷時文化名城蓮城在省內外的知名度日趨提升，旅游業發展潛力巨大。為了靠近主要經濟據點，吸引當地客貨流，可行性研究階段對靠近廣南縣城的派播站位方案進行了深入研究，同時研究了昔板站位方案、派播站位方案、板構站位方案和上鍋寨站位方案，見圖1。

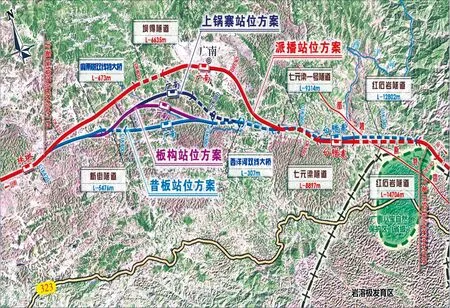
圖1 廣南站位方案比較示意

根據本工程評價需要，選取線路總長度、拆遷建筑物、吸引客貨流的能力等定量和定性相結合的12個指標，分別用C1，C2，…，C12表示(其中C8，C11，C12為效益型指標，其余都為成本型指標)。通過對該段鐵路可研報告的整理，得出上述4個方案各指標取值的基礎數據，并聘請專家采用語言類模糊數對定性指標進行賦值，見表3。

4.1 方案評價和比選

(1)定性指標的語言類模糊數取值量化為三角模糊數，見表4。

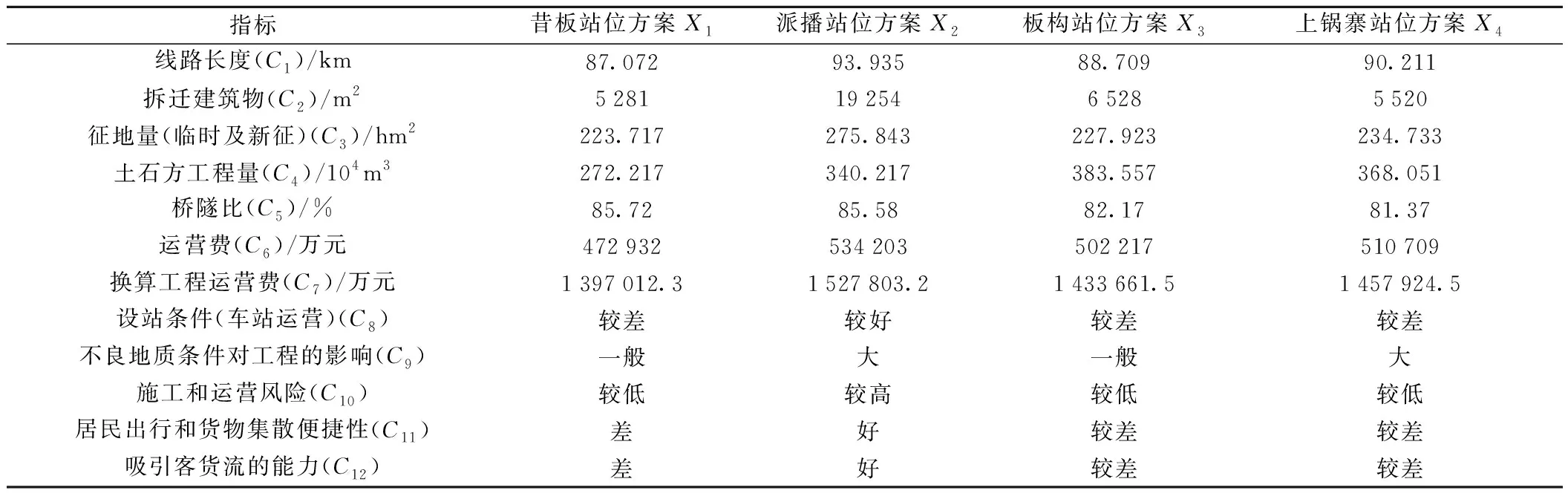
表3 各站位方案及對應指標的取值

表4 定性指標量化值

(2)將定性指標取值的三角模糊數與定量指標取值精確實數結合起來，構成線路方案評價的決策矩陣A=(aij)4×12。然后分別利用式(9)、式(10)和式(11)、式(12)對決策矩陣進行規范化處理，得到規范化矩陣

(3)利用式(6)確定指標權重，得到

W=(0.009 0，0.105 4，0.023 4，0.041 8，0.007 3，0.014 1，0.010 5，0.129 1，0.132 2，0.129 1，0.199 1，0.199 1)。

(4)用權重W對規范化矩陣S進行加權，得到加權規范化矩陣Y，并計算得到正負理想方案。然后，計算各備選方案到正理想方案與負理想方案的距離，并得到各方案的綜合相對貼近度為

P1=0.270 3，P2=0.730 1，

P3=0.419 0，P4=0.288 5

因此，方案排序結果為X2>X3>X4>X1，派播站位方案比其他3個站位方案更優。

4.2 結果分析

對表3給出的4個站位方案的指標數據進行分析可知，派播站位方案線路最長、征地拆遷工程最多、橋隧比和換算工程運營費都很高，但該方案有利于吸引客貨流、方便旅客出行和貨物集散以及設站條件最好，由于這3個定性指標的權重相對更大，使得派播站位方案的綜合評價值仍然達到了0.7以上，也是4個站位方案中經綜合定性、定量比較后的最優方案。上述計算得出的結果與設計單位專家通過對定量指標的計算和對定性指標的分析后所做出的決策結論一致。

5 結論

根據鐵路站位方案評價和比選的特點，建立了基于混合多屬性決策的方案評價模型。模型彌補了層次分析法和模糊綜合評價等傳統評價方法的不足，根據指標原始數據的差異性大小確定指標權重，使得權重趨于更科學、合理；同時，利用混合多屬性決策，實現了定量指標和定性指標的綜合比選，使得決策結果更加均衡化。最后實例分析表明，本文模型可為鐵路站位方案比選提供定量化的決策支持，具有較好的可靠性和實用價值。

[1] 周承漢.基于三角模糊數的高速鐵路線站位方案比選[J].鐵道科學與工程學報，2016，13(3)：435-440.

[2] 唐經勇.高速鐵路客運站選址方法研究[D].成都：西南交通大學，2008.

[3] 張世升.基于鐵路沿線大型站點的綜合開發研究——以日本京都火車站綜合體談西安站改[J].鐵道標準設計，2016，60(1)：114-118.

[4] 喬俊飛.鄭州至新鄭機場城際鐵路機場段線路方案研究[J].鐵道標準設計，2016，60(1)：52-55.

[5] 羅圓，姚令侃，朱穎.基于離差投影的山區鐵路選線方案比選模型[J].鐵道標準設計，2013，57(10)：1-6.

[6] 羅圓，姚令侃，朱穎.基于效用理論的鐵路選線方案比選模型[J].西南交通大學學報，2013，48(6)：1008-1015.

[7] 羅圓.基于不確定性分析的鐵路選線方案評價方法研究[D].成都：西南交通大學，2016.

[8] 閆創.西安至韓城城際鐵路線路走向方案研究[J].鐵道標準設計，2016，60(8)：40-44.

[9] 陳俊，邵海鵬.鐵路選線設計方案物元優選模型[J].鐵道標準設計，2011(3)：5-8.

[10] 周宏安，劉三陽.基于離差最大化模型的模糊多屬性決策投影法[J].系統工程與電子技術，2007，29(5)：741-744.

[11] 楊靜，邱菀華.基于離差的模糊多屬性決策法及其應用[J].系統工程，2008，26(6)：107-110.

[12] 夏勇其，吳祈宗.一種混合型多屬性決策問題的TOPSIS方法[J].系統工程學報，2004，19(6)：630-634.

[13] 許海霖，張晶.基于改進TOPSIS模型的地鐵網絡節點重要性評價方法[J].鐵道標準設計，2016，60(7)：19-24

[14] 廖勇.基于三角模糊數的鐵路客運站選址方案評價方法[J].中國鐵道科學，2009，30(6)：119-125.

[15] 賀曉霞，鮑學英，王起才.基于組合方法計算權重的綠色鐵路客站綜合評估[J].鐵道標準設計，2016，60(4)：103-107.