一種水聲寬帶雙曲調頻信號波達方向估計方法

李 軍， 林 秋 華， 王 凱， 康 春 玉， 楊 秀 庭

( 1.大連理工大學 電子信息與電氣工程學部 信息與通信工程學院， 遼寧 大連 116024；2.海軍大連艦艇學院 水武與防化系， 遼寧 大連 116018；3.大連東軟信息學院 計算機科學與技術系， 遼寧 大連 116023 )

0 引 言

寬帶線性調頻(linear frequency modulation，LFM)信號在通信、雷達、聲吶等領域有著廣泛的應用[1-2]．與電磁波及其傳播的大氣環境相比，水下聲波具有更低的傳播速度和更加復雜的海洋傳播環境．主動聲吶探測脈沖如果采用LFM信號，會產生較大的多普勒頻移進而導致匹配濾波嚴重失配，影響主動聲吶的探測性能．因此，借鑒蝙蝠、海豚等生物的回聲定位系統，主動聲吶在定位過程中一般發射具有多普勒不變性的寬帶雙曲調頻(hyperbolic frequency modulation，HFM)信號[3-5]．在海戰場環境中，存在大量的HFM信號，水面艦艇或潛艇如何應用被動拖曳線列陣聲吶實現對這些信號的識別、定位值得深入研究．

目標方向被動估計也被稱為信號波達方向(direction of arrival，DOA)估計，由于不需要向外界發射信號，平臺自身具有很好的隱蔽性．針對寬帶調頻信號的DOA估計問題一直是國內外研究的熱點[6-12]．陶然等[6-8]根據分數階傅里葉域LFM信號的高聚焦性，首先提出了基于分數階傅里葉變換(fractional Fourier transform，FRFT)和多重信號分類(multiple signal classification，MUSIC)算法的LFM信號高分辨DOA估計方法(FRFT-MUSIC)，并在雷達信號DOA估計領域得到了大量的應用．Cui等[9]針對多途環境下LFM信號，結合FRFT和旋轉不變技術(estimated by the signal parameters via rotation invariance technique，ESPRIT)提出了一種新的DOA估計方法(FRFT-ESPRIT)，實現了多途條件下寬帶相干LFM信號DOA估計．Jin等[10]將FRFT和虛擬陣列變換相結合，解決了常規MUSIC 算法和ESPRIT算法中相干信號的發現問題．王瑞等[11]對FRFT-MUSIC算法中心頻率估計進行了改進，提高了DOA估計精度．劉德亮等[12]提出了一種短快拍條件下LFM信號DOA估計方法，僅依靠少量快拍即可實現對LFM信號的高分辨率DOA估計．在水聲信號處理中，陳艷麗等[13-14]研究了基于FRFT的水下LFM信號的檢測和參數估計問題，李軍等[15]應用FRFT實現了水聲LFM信號的被動測向和測距．這些方法主要都是針對LFM信號進行信號參數和DOA估計．LFM與HFM信號都是調頻信號，LFM信號頻率呈線性變化，應用FRFT技術可實現較好的定位效果，然而HFM信號的頻率呈非線性變化，直接應用FRFT技術進行DOA估計則會產生一定的誤差，如何有效利用FRFT技術提高在聲吶領域有著廣泛應用的HFM信號DOA估計精度是一個亟待解決的問題．

針對寬帶HFM信號的DOA估計問題，本文結合短時分數階傅里葉變換(short-time fractional Fourier transform，STFRFT)的基本思想和MUSIC 算法提出一種基于STFRFT的寬帶HFM信號DOA估計方法，簡稱STFRFT-MUSIC，并通過仿真實驗，對本文方法的有效性進行驗證．

1 基本理論

首先給出LFM、HFM信號的基本模型，推導兩種信號初始頻率、截止頻率、中心頻率和調頻率之間的關系，并結合分段線性化思想用多個STLFM信號表示HFM信號，在此基礎上建立均勻線列陣遠場寬帶HFM信號接收數據模型．

1.1 LFM信號模型

設fl、fh分別為LFM信號的初始頻率和截止頻率，μ為信號的調頻率，T為周期，則LFM信號模型[1-2]為

s(t)=A(t)[exp(-jπ(2flt+μt2))]；t∈[0，T]

(1)

LFM信號的瞬時頻率fsa(t)=fl+μt，LFM信號的初始頻率、截止頻率與調頻率之間的關系為

fh=fl+μT，μ=(fh-fl)/T

(2)

1.2 HFM信號模型

設fz為HFM信號的中心頻率，g為信號頻率變化率，T為周期，則HFM信號模型[3-4]為

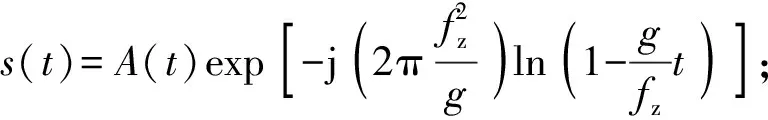
t∈[-T/2，T/2]

(3)

HFM信號的瞬時頻率為

(4)

設fl=fsa(-T/2)，fh=fsa(T/2)分別為HFM信號的初始頻率和截止頻率，即

(5)

瞬時頻率fsa(t)在fl和fh之間連續單調，服從雙曲分布．HFM信號的帶寬B=fh-fl．根據式(4)、(5)可以推導出HFM信號fl、fh、fz和g之間關系：

(6)

(7)

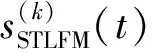
(8)

1.3 HFM信號陣列接收模型

設均勻線列陣聲吶有M個陣元，間距為d，其中1號陣元為參考陣元．遠場環境存在Q個寬帶HFM信源，其陣列接收數據模型如圖1所示．

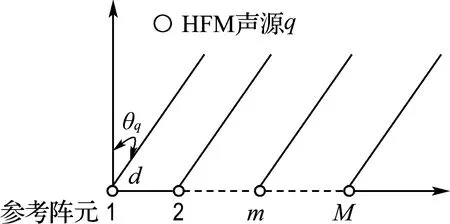
圖1 均勻線列陣聲吶遠場寬帶HFM信號接 收模型Fig.1 The wideband HFM signal receiving model with uniform linear array sonar in far field

根據式(8)，第q個HFM信號用K個STLFM信號可以近似地表示為

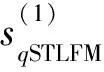
q=1,2,…,Q

(9)

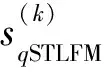
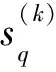
q=1，2，…,Q，k=1，2，…,K

(10)

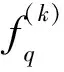
設θq為第q個信號到均勻線列陣的入射角，c為聲速，第q個信號到達第m個陣元時相對于參考陣元(1號陣元)的時延τqm為[6-7]

τqm=(m-1)dsinθq/c

(11)

則第m個陣元的接收信號時域表示形式為

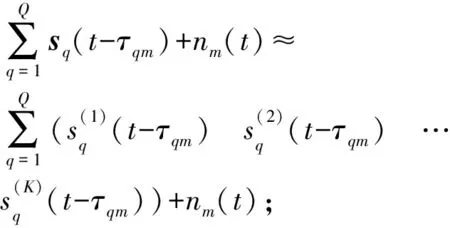
m=1，2，…，M

(12)

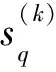
X(t)=(X(1)(t)X(2)(t) …X(K)(t))

(13)

(14)

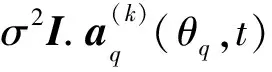
(15)

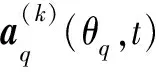
2 短時分數階傅里葉域HFM信號DOA估計方法

本文利用短時分數階傅里葉域HFM信號接收模型代替傳統的陣列數據模型，將HFM信號時變陣列流形矩陣變換為多個短時固定的陣列流形矩陣，利用MUSIC算法實現多個HFM信號的高分辨DOA估計．

2.1 短時分數階傅里葉域HFM信號接收模型

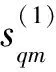
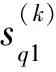
(16)

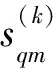
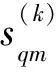
(17)

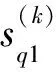
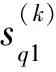
n=-(N-1)/2，…，0，…，(N-1)/2

(18)

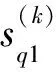
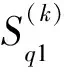
(19)

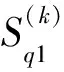
(20)

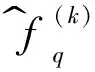
f^(k)q

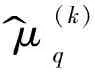
μ^(k)q

設(，)為第k時段STLFM信號的初始頻率和調頻率估計值，可由式(20)完成估計．

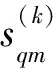
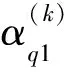
(21)

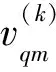
(22)

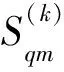
(23)

其中

(24)

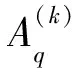
(25)

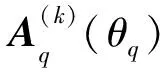
(26)

選擇分數階傅里葉域Q個峰值點上的數據作為第m個陣元上的第k時段接收數據的分數階傅里葉域輸出：

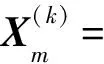
(27)

陣列所有陣元接收信號的第k時段分數階傅里葉域輸出為

(28)

將K個時段的分數階傅里葉域輸出組合在一起就可以得到遠場寬帶HFM信號在分數階傅里葉域的接收數據模型

X=(X(1)X(2)…X(K))

(29)

其中

X(k)=A(k)(θ)S(k)+N

(30)

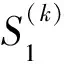
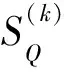
(31)

2.2 HFM信號DOA估計方法

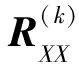
(32)

(33)

將各個時段信號得到的空間譜進行求和運算得到第q個HFM信號的STFRFT-MUSIC空間譜為

(34)

對上式進行最大值搜索，STFRFT-MUSIC空間譜Pq(θ)最大值對應的坐標θq即為第q個信號的DOA估計．

綜上所述，給出本文提出的STFRFT-MUSIC 算法的具體實現步驟：

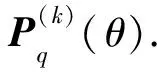
(8)重復(2)～(7)，分別得到第q個HFM信號在各個時段上的STFRFT-MUSIC空間譜．

(9)由式(34)得到第q個HFM信號對應的STFRFT-MUSIC空間譜Pq(θ)，極大值對應的方位角θmax為該信號DOA估計．

(10)如果有多個HFM信號，重復(2)～(9)，逐一得到每個信號對應的DOA估計．

3 仿真實驗

為了驗證本文方法的有效性，開展了3種仿真實驗．首先，對LFM、HFM、STLFM信號的頻譜分布情況進行了仿真研究；其次，以拖曳線列陣為背景仿真研究了傳統FRFT-MUSIC方法和本文STFRFT-MUSIC方法對HFM信號頻譜和DOA估計的性能；最后，重點分析了時域分段數、信噪比和目標方位等對算法性能的影響．

3.1 HFM與STLFM信號頻譜分析

設主動聲吶信號的脈沖寬度T=1 s，初始頻率fl=1 kHz、截止頻率fh=2 kHz，LFM信號與HFM信號頻譜分布見圖2，LFM信號的頻率特性呈線性單調遞增，而HFM信號的頻率特性呈非線性單調遞增．如果將HFM信號在時域分別等分成2、5、10段，每一段信號都用一個STLFM信號來代替，新的多段STLFM信號的頻譜分布見圖2，可以看出，隨著時域分段數的逐步增加，用多個STLFM信號來近似表示HFM信號是可行的．

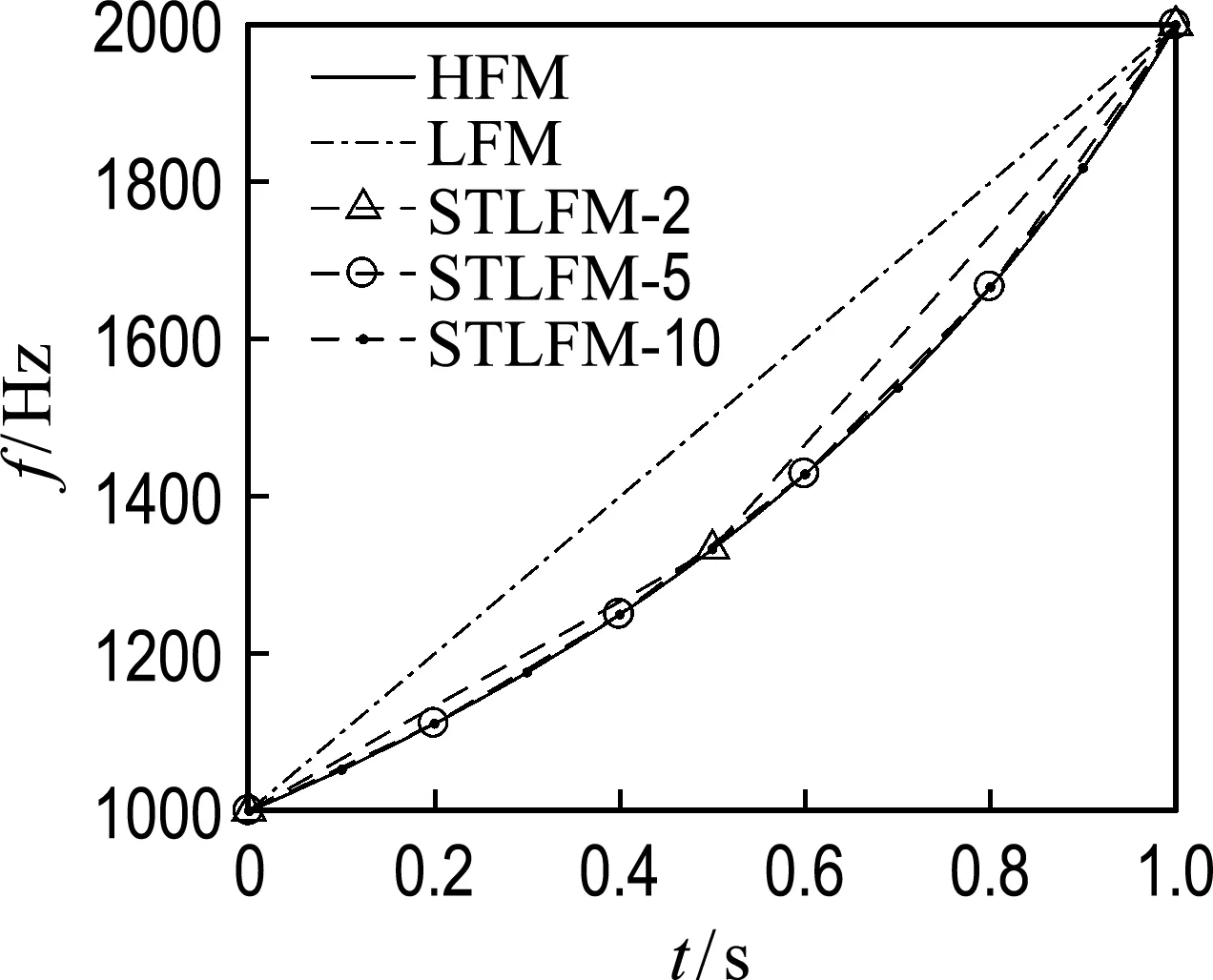
圖2 LFM信號和HFM信號的頻譜Fig.2 The spectrum of LFM signal and HFM signal

3.2 時域分段與頻率估計分析

仿真實驗中，原始信號采用上節仿真中的HFM信號，線列陣陣元數M=100，陣元間距d=0.2 m，聲速c=1 500 m/s，采樣頻率fs=48 kHz，目標位于0°，方位掃描步長0.01°，噪聲為信噪比為-3 dB的加性高斯白噪聲．

根據本文所提出的方法，首先應該在時域對接收數據進行分段處理，本節重點研究具體的分段數對算法性能的影響．根據式(19)和(20)，應用分數階傅里葉變換可以實現對原始信號初始頻率和調頻率的估計，當時域信號不分段和分段數分別為2、5、10時，圖3給出了本文方法對HFM信號頻率分布的估計情況．當時域不分段時，就是基于FRFT方法對HFM信號進行參數估計，可以看出初始頻率要遠高于HFM信號的初始頻率(1 kHz)，而截止頻率要遠低于HFM信號的截止頻率(2 kHz)．當分段數為2時，頻率參數的估計誤差依然較大；當分段數增加到5時，頻率參數的估計性能得到大幅的提高；當分段數增加到10時，對HFM信號的頻率估計已經非常逼近原始信號．因此在后續的仿真過程中在時域將接收數據分成5段或10段來完成HFM信號的DOA估計．

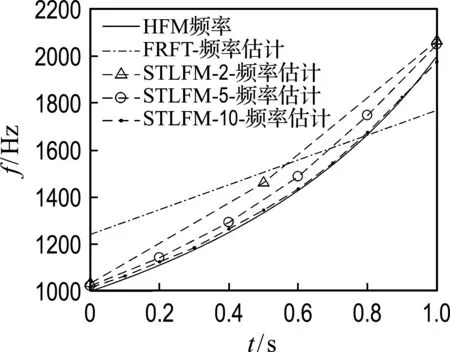
圖3 不同時域分段數條件下頻率估計情況Fig.3 Frequency estimation under different time domain piecewise numbers

圖4給出了分別應用FRFT-MUSIC和STFRFT-MUSIC方法對HFM目標信號進行DOA估計的空間譜，其中STFRFT-MUSIC-5和STFRFT-MUSIC-10分別表示在時域分成5段和10段進行DOA估計．可以看出由于STFRFT-MUSIC 方法在時域進行了分段處理，對HFM信號的參數估計比較準確，因此在后續的仿真實驗中對HFM信號的DOA(θq)估計誤差較小，隨著分段數的增多主瓣寬度會逐漸變窄，旁瓣抑制效果也逐漸變好，與FRFT-MUSIC方法相比具有較高的方位分辨率和估計精度．

通過本節仿真可以看出雖然隨著時域分段數的增加本文STFRFT-MUSIC方法的探測性能會逐步提高，在理論上隨著時域分段數的無限增大STFRFT所估計出的HFM信號頻率分布情況將無限逼近原始信號的頻率分布情況，但這是建立在系統采樣頻率足夠大的基礎之上．在實際的主動聲吶系統中，采樣頻率一般為固定值，隨著分段數的增大，每段時長將隨之減小，對應的采樣點數也相應減少．由于海洋環境的復雜性和聲傳播多途效應的影響，較少的采樣點數必然會影響STFRFT-MUSIC方法的估計性能，因此在實際使用過程中時域分段數不宜過高．由于涉及時域的分段，STFRFT-MUSIC方法對于脈沖寬度較小、頻率變化不大的近程主動聲吶不具備優勢，而對于脈沖寬度大于0.5 s、頻率變化率范圍大于0.5 kHz的遠程低頻主動聲吶則具有明顯優勢．

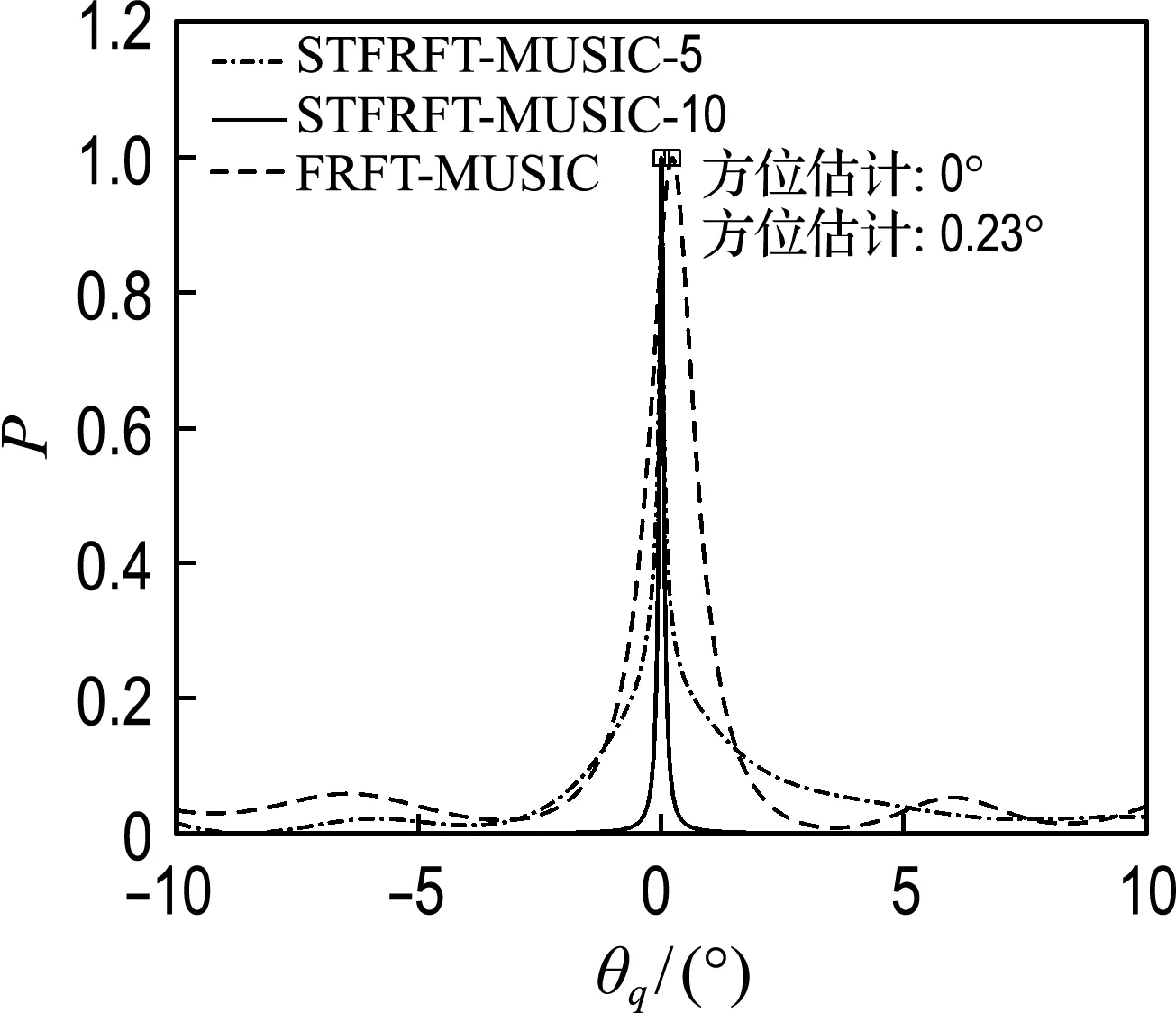
圖4 STFRFT-MUSIC與FRFT-MUSIC空間譜Fig.4 The spatial spectrum of STFRFT-MUSIC and FRFT-MUSIC

3.3 信噪比對算法性能的影響

本節采用蒙特卡羅仿真分析方法研究信噪比和目標方位對算法性能的影響，應用均方根誤差(estimated root mean-square error，erms)來評價算法DOA估計性能：

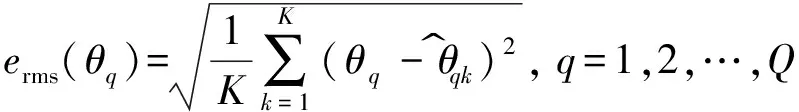
erms(θq)=1K∑Kk=1(θq-θ^qk)2, q=1,2,…,Q

(35)

式中：θq為第q個HFM信號的真實方位，

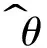
θ^

qk為第k次仿真DOA估計值，K為蒙特卡羅仿真次數．

設HFM目標信號位于10°，其他仿真條件同上節，當信噪比從-20 dB變化到20 dB時，分別應用FRFT-MUSIC與STFRFT-MUSIC方法進行DOA估計，圖5給出了不同信噪比Rsn條件下兩種方法的DOA估計空間譜，圖6給出了通過100次蒙特卡羅仿真后兩種方法在不同信噪比下DOA估計的均方根誤差曲線．

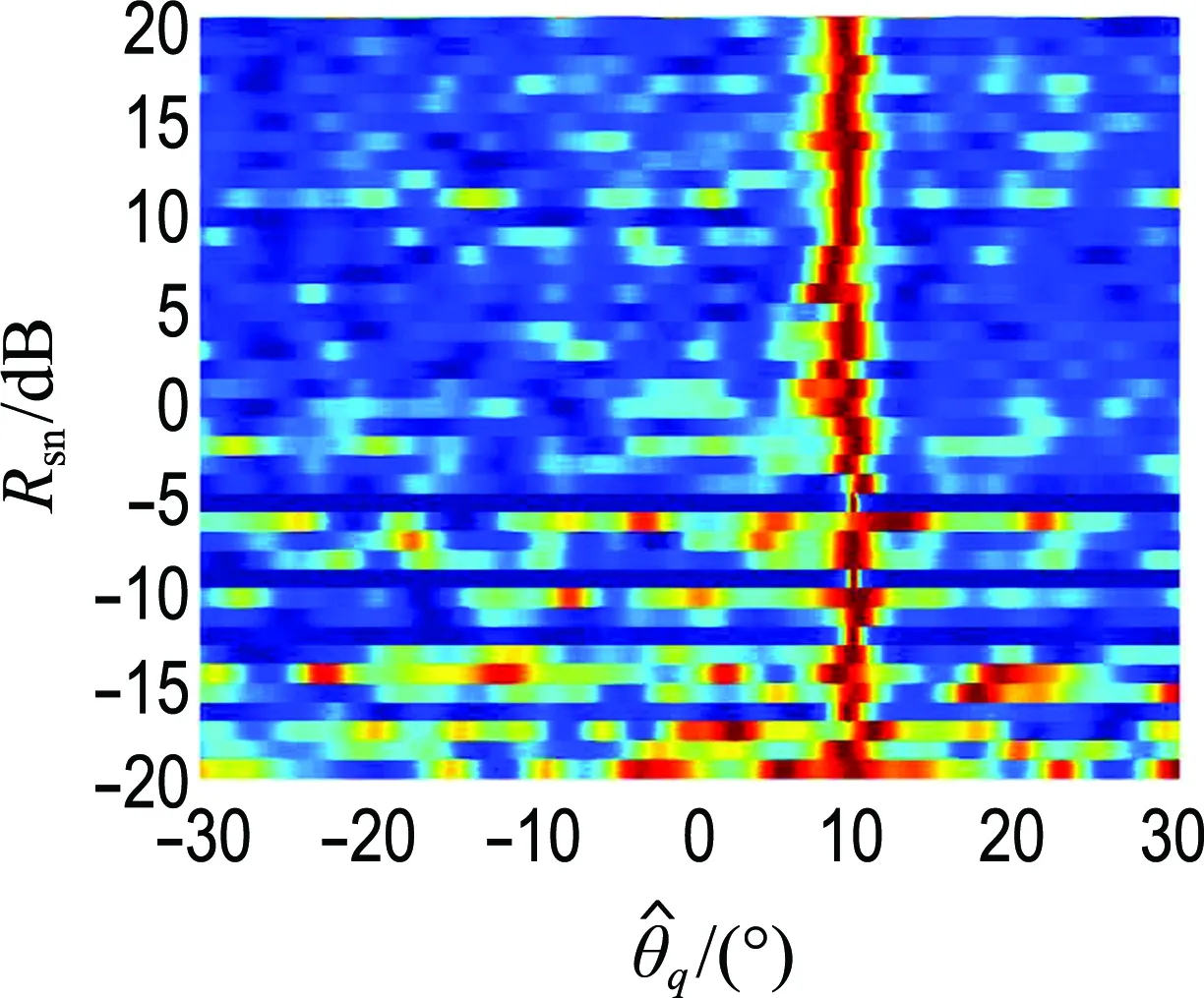
(a) FRFT-MUSIC

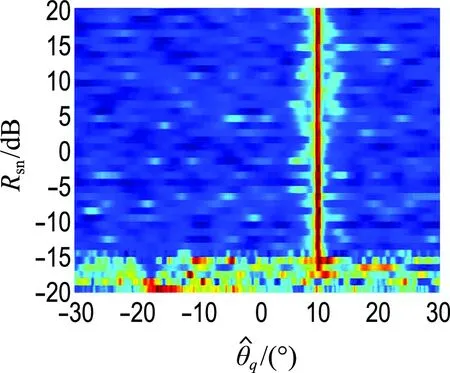
(b) STFRFT-MUSIC-5

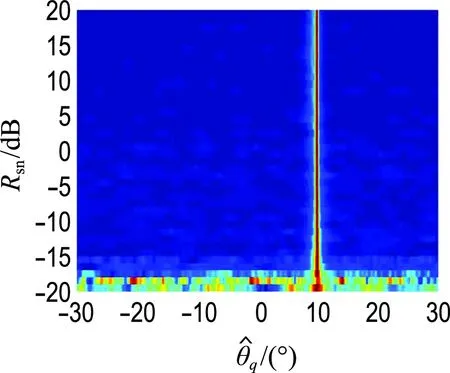
(c) STFRFT-MUSIC-10

圖5 兩種方法在不同SNR條件下DOA估計

Fig.5 DOA estimation of two methods under different SNR

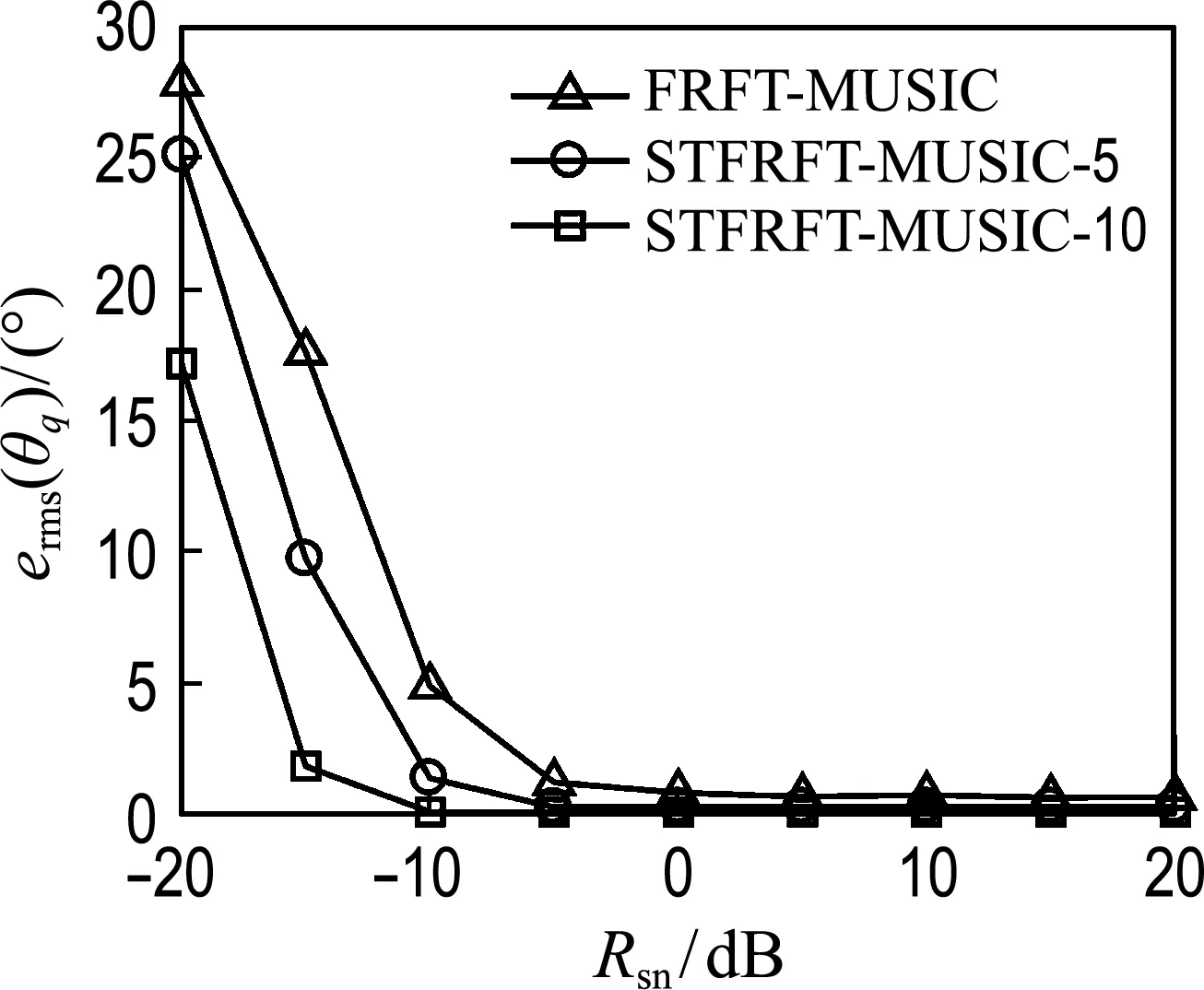
圖6 不同信噪比條件下兩種方法的均方 根誤差曲線Fig.6 The RMSE curve of two methods under different SNR

可以看出，FRFT-MUSIC方法在信噪比高于-5 dB時能夠對目標DOA進行有效估計，但始終存在系統誤差；STFRFT-MUSIC-5和STFRFT-MUSIC-10分別在信噪比高于-10 dB和-15 dB時可對目標DOA進行有效估計，STFRFT-MUSIC方法的系統誤差要遠小于FRFT-MUSIC 方法，該系統誤差隨著時域分段數的增多而逐漸減小．

上述仿真是針對噪聲為高斯白噪聲的情況，下面考慮噪聲為有色噪聲情況，設噪聲的能量主要分布在1.35～1.55 kHz，兩種方法在該有色噪聲干擾下DOA估計的均方根誤差曲線如圖7所示．

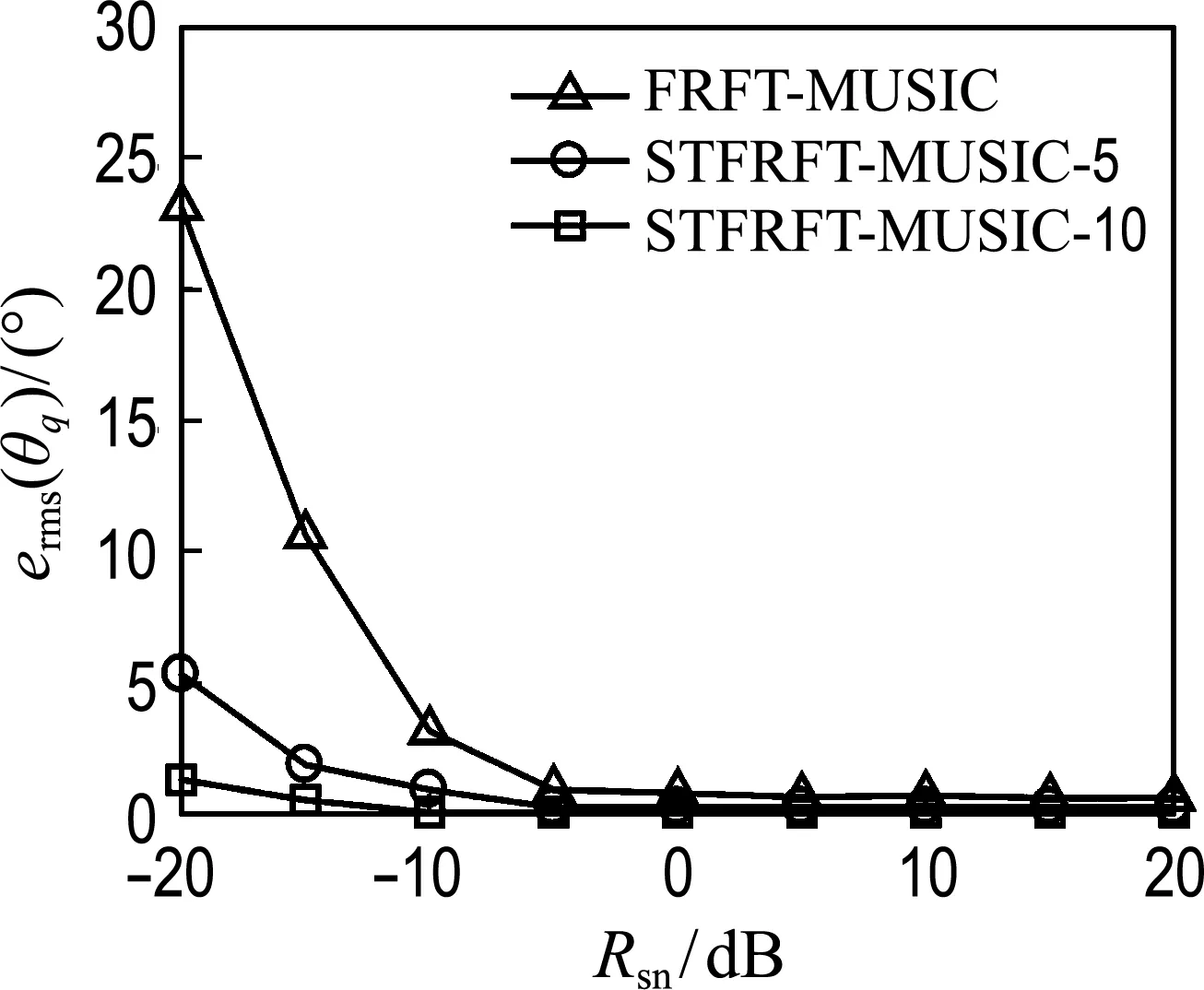
圖7 有色噪聲干擾下兩種方法的均方根誤差曲線Fig.7 The RMSE curve of two methods under colored noise

可以看出，有色噪聲對STFRFT-MUSIC方法的影響有限，而對FRFT-MUSIC方法的影響則較大，這是由于STFRFT-MUSIC方法采用了時域分段處理．對于STFRFT-MUSIC-5方法而言，該有色噪聲干擾的是第2、3時段信號，對其他3個時段信號的干擾不大；對于STFRFT-MUSIC-10 方法而言，其干擾的是第4、5、6段信號，對于其他7個時段信號的干擾不大．STFRFT-MUSIC 方法對于干擾頻段內短時信號DOA估計性能較差，但對其他頻段的短時信號DOA估計則較好，根據式(34)STFRFT-MUSIC方法最終的DOA估計結果是多個時段信號DOA估計結果的和，因此該有色噪聲對STFRFT-MUSIC方法的影響有限．對于FRFT-MUSIC方法，由于沒有在時域對信號進行分段處理，在DOA估計過程中將受有色噪聲干擾的HFM信號作為一個整體進行參數的估計，噪聲對其參數估計的影響較大，進而影響了DOA估計性能，因此本文方法的抗有色噪聲干擾能力要高于FRFT-MUSIC方法．

3.4 目標方位對算法性能的影響

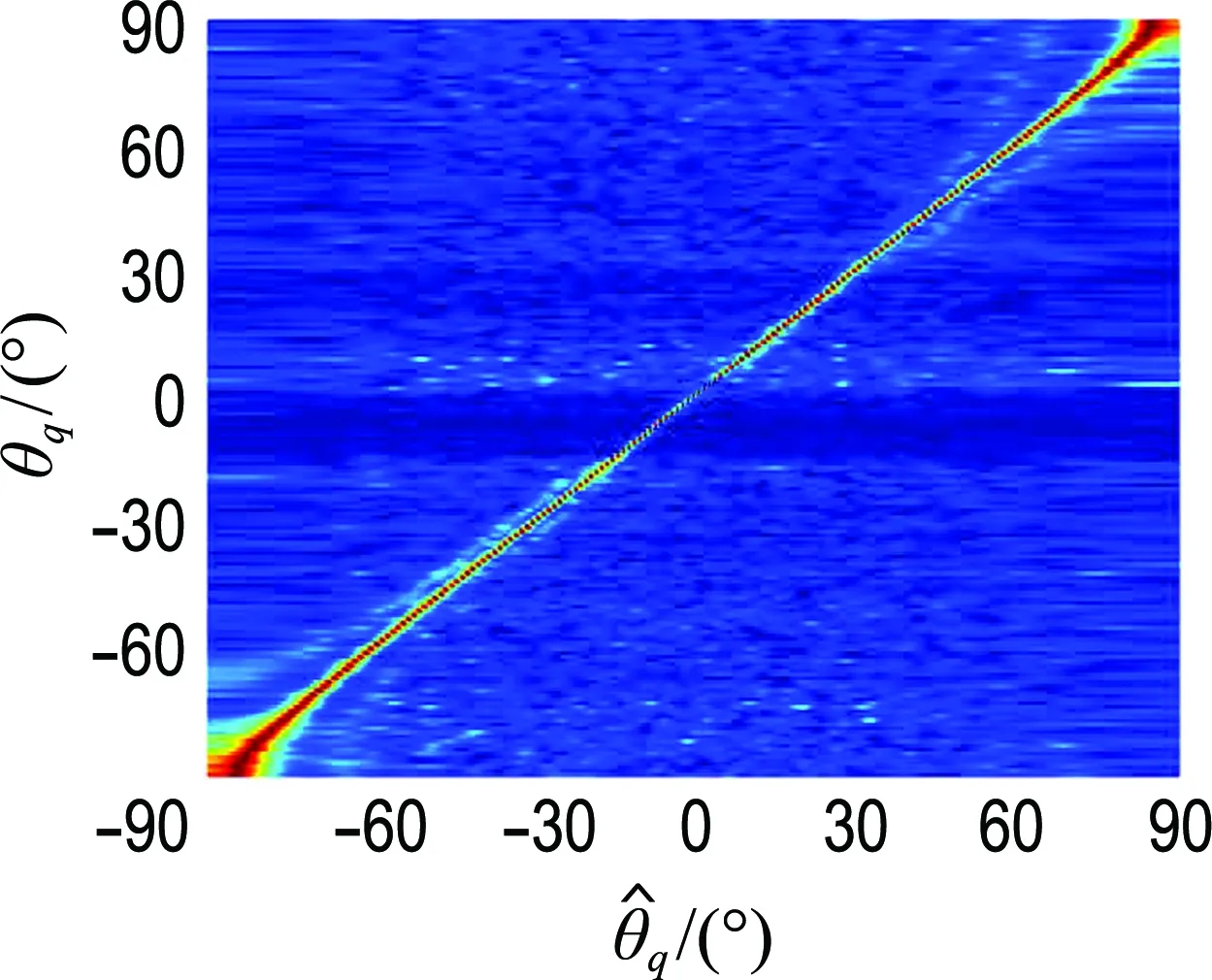
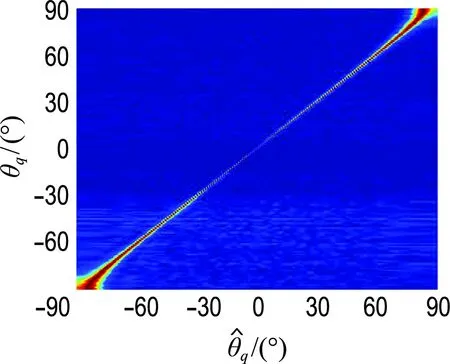
本節研究目標方位變化對算法性能的影響，基本仿真條件同上節，噪聲為高斯白噪聲，信噪比為-3 dB，設HFM目標信號方位從-90°變化到90°，圖8給出了不同目標方位條件下兩種方法的DOA估計空間譜，圖9給出了通過100次蒙特卡羅仿真后兩種方法在不同目標方位條件下DOA估計的均方根誤差曲線．可以看出，兩種方法對0°方向目標估計誤差最小，隨著目標方位角的增大，誤差會逐漸增大，當目標方位角大于70°時DOA估計誤差增大明顯．在方位估計精度方面STFRFT-MUSIC-10最好，STFRFT-MUSIC-5次之，FRFT-MUSIC最差．

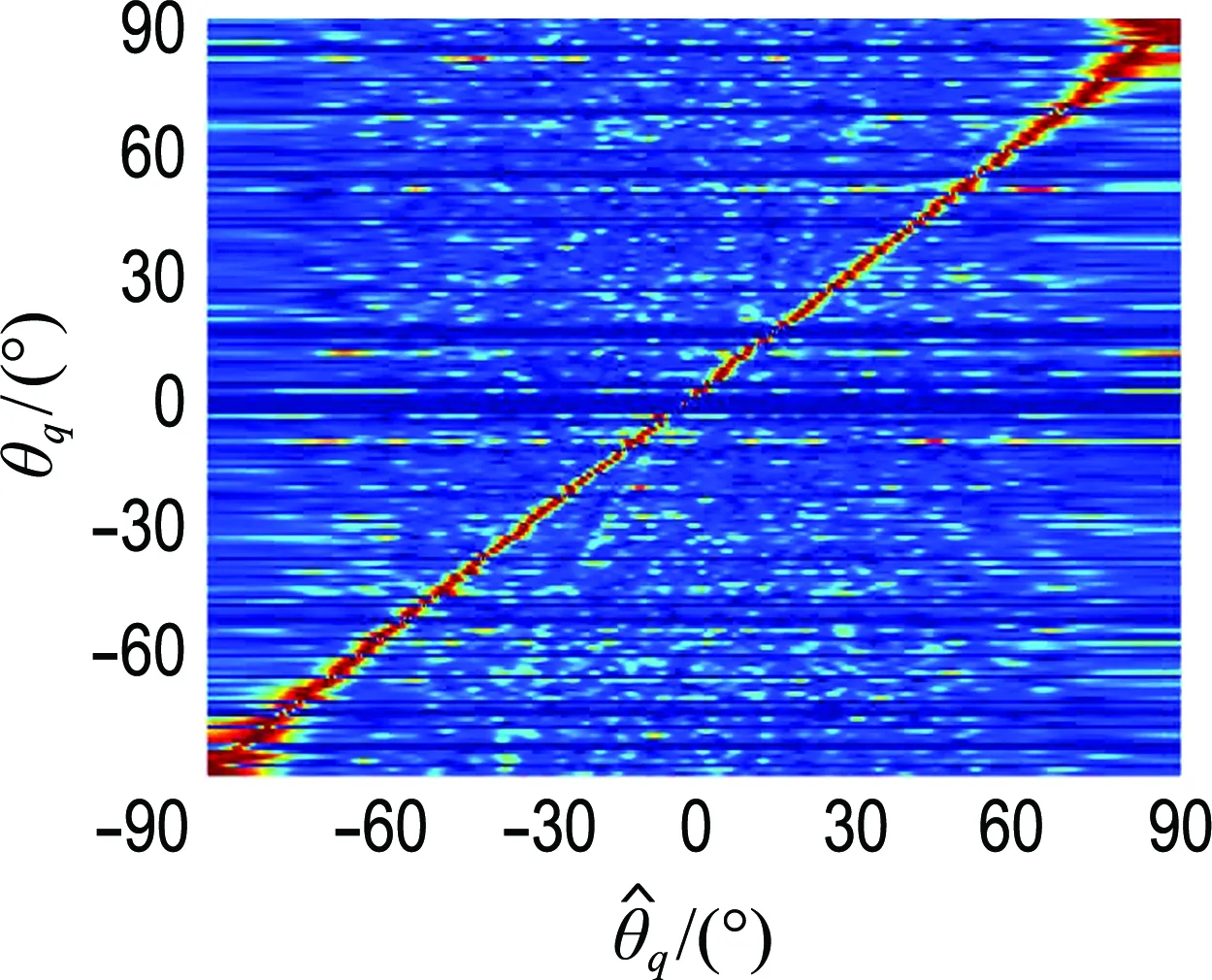
(a) FRFT-MUSIC

(b) STFRFT-MUSIC-5

(c) STFRFT-MUSIC-10

圖8 兩種方法在不同目標方位條件下DOA估計

Fig.8 DOA estimation of two methods under different target azimuth

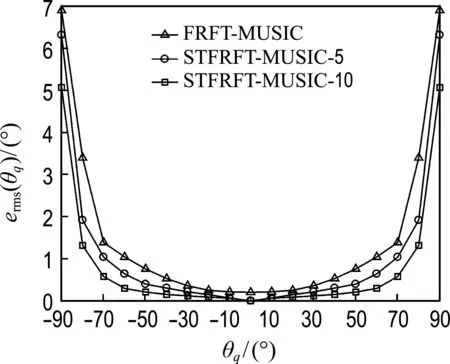
圖9 不同目標方位條件下兩種方法的均方 根誤差曲線Fig.9 The RMSE curve of two methods under different target azimuth

4 結 語

針對海戰場環境中大量存在的寬帶HFM信號DOA估計問題，本文結合短時分數階傅里葉變換思想，提出了一種基于STFRFT的HFM信號DOA估計方法．通過仿真實驗，對LFM、HFM、STLFM等信號的頻譜進行了分析，研究了時域分段數、信噪比、目標方位等對算法性能的影響，對該方法的有效性進行了驗證．與傳統方法相比，本文方法具有較高的方位分辨率和估計精度，在被動拖曳線列陣聲吶或多基地聲吶系統中有著廣泛的應用前景．

[1] BARBAROSSA S. Analysis of multicomponent LFM signals by a combined Wigner-Hough transform [J].IEEETransactionsonSignalProcessing, 1995,43(6):1511-1515.

[2] LEE D H, SHIN J W, DO D W,etal. Robust LFM target detection in wideband sonar systems [J].IEEETransactionsonAerospace&ElectronicSystems, 2017,53(5):2399-2412.

[3] 朱 埜,倪伯林. 動物聲吶信號在魚雷中的應用[J]. 聲學學報, 1999,24(1):29-44.

ZHU Ye, NI Bolin. Application of animal sonar signals in torpedoes [J].ActaAcustica, 1999,24(1):29-44.(in Chinese)

[4] 龐玉紅,嚴 琪,王世闖. 基于瞬時頻率的雙曲調頻信號距離估計誤差分析[J]. 聲學技術, 2016,35(5):421-425.

PAN Yuhong, YAN Qi, WANG Shichuang. Instantaneous-frequency-based ranging bias analysis of HFM waveforms [J].TechnicalAcoustics, 2016,35(5):421-425. (in Chinese)

[5] DUTTA-ROY A. Radar spectrum engineering and management:technical and regulatory issues [J].ProceedingsoftheIEEE, 2015,103(1):77-84.

[6] 陶 然,周云松. 基于分數階傅里葉變換的寬帶LFM信號波達方向估計新算法[J]. 北京理工大學學報, 2005,25(10):895-899.

TAO Ran, ZHOU Yunsong. A novel method for the direction of arrival estimation of wideband linear frequency modulated sources based on fractional Fourier transform [J].TransactionsofBeijingInstituteofTechnology, 2005,25(10):895-899. (in Chinese)

[7] 楊小明,陶 然. 基于分數階傅里葉變換的線性調頻信號二維波達方向估計[J].電子學報, 2008,36(9):1737-1740.

YANG Xiaoming, TAO Ran. 2-D DOA estimation of LFM signals based on fractional Fourier transform [J].ActaElectronicaSinica, 2008,36(9):1737-1740. (in Chinese)

[8] LIU Shengheng, SHAN Tao, ZHANG Yimin D,etal. A fast algorithm for multi-component LFM signal analysis exploiting segmented DPT and SDFrFT [C] //2015IEEEInternationalRadarConference. Arlington: IEEE, 2015:1139-1143.

[9] CUI Yue, LIU Kaihua, WANG Junfeng. Direction of arrival estimation of coherent wideband LFM signals in multipath environment [C] //2010IEEE10thInternationalConferenceonSignalProcessing,ICSP2010. Beijing: IEEE, 2010:58-61.

[10] JIN Xiang, ZHANG Tianqi, BAI Juan,etal. DOA estimation of coherent wideband LFM signals based on fractional Fourier transform and virtual array [C] //Proceedings-20103rdInternationalCongressonImageandSignalProcessing,CISP2010. Yantai: IEEE, 2010:4380-4384.

[11] 王 瑞,馬 艷. 基于分數階傅里葉變換的線性調頻脈沖信號波達方向估計[J]. 兵工學報, 2014,35(3):421-427.

WANG Rui, MA Yan. DOA estimation of wideband linear frequency modulated pulse signals based on fractional Fourier transform [J].ActaArmamentarii, 2014,35(3):421-427. (in Chinese)

[12] 劉德亮,劉開華,于潔瀟,等. 短快拍條件下寬帶chirp信號的波達方向估計[J]. 計算機應用, 2015,35(2):351-353.

LIU Deliang, LIU Kaihua, YU Jiexiao,etal. DOA estimation for wideband chirp signal with a few snapshots [J].JournalofComputerApplications, 2015,35(2):351-353. (in Chinese)

[13] 陳艷麗,郭良浩,宮在曉. 簡明分數階傅里葉變換及其對線性調頻信號的檢測和參數估計[J]. 聲學學報, 2015,40(6):761-771.

CHEN Yanli, GUO Lianghao, GONG Zaixiao. The concise fractional Fourier transform and its application in detection and parameter estimation of the linear frequency-modulated signal [J].ActaAcustica, 2015,40(6):761-771. (in Chinese)

[14] 李秀坤,孟祥夏,夏 峙. 水下目標幾何聲散射回波在分數階傅里葉變換域中的特性[J]. 物理學報, 2015,64(6):064302.

LI Xiukun, MENG Xiangxia, XIA Zhi. Characteristics of the geometrical scattering waves from underwater target in fractional Fourier transform domain [J].ActaPhysicaSinica, 2015,64(6):064302. (in Chinese)

[15] 李 軍,林秋華,楊秀庭,等. 近場寬帶LFM信號被動測向和測距方法[J]. 系統工程與電子技術, 2016,38(8):1737-1743.

LI Jun, LIN Qiuhua, YANG Xiuting,etal. Passive DOA and range estimation method for near-field broadband LFM signals [J].SystemsEngineeringandElectronics, 2016,38(8):1737-1743. (in Chinese)

[16] OZAKTAS H M, ARIKAN O, KUTAY M A,etal. Digital computation of the fractional Fourier transform [J].IEEETransactionsonSignalProcessing, 1996,44(9):2141-2150.