多項時間-空間分數階微分方程的PIM求解

危國華

（福建廣播電視大學 三明分校，福建 三明 365000）

近年來研究者們發現分數階微分方程比經典的整數階微分方程更為準確的描述現實生活中的各種現象，尤其分數階擴散方程已被廣泛用來描述特征方差尺度為時間的冪次的反常擴散過程。隨后學者們討論分數階微分方程的數值解法[1-9]。本文嘗試采用差分/多項式基點插值配置法處理多項時間-空間分數階微分方程，提出半離散格式以及全離散格式，并通過數值例子驗證方法的有效性。

討論如下多項的時間-空間分數階微分方程：

帶有初邊值條件：

其中d1，d2，…，dk，γ1，γ2，…，γk，κβ，κ0，κ1都是非負常數，且表示函數 u（x，t）對時間變量t的γl階Caputo分數階導數[10]，即表示函數u（x，t）對空間變量x的β（1＜β＜2）階Riemann-Liouville分數階導數[10]，即

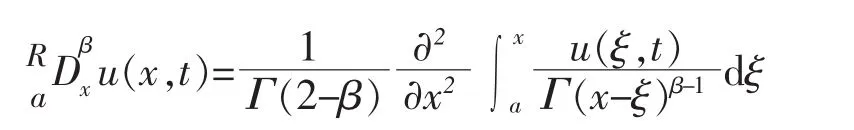
這里Γ（·）為伽馬函數。

本文假設時間-空間分數階微分方程(1-3)的解

1 離散格式

1.1 半離散格式

首先離散時間變量，令 tn=nτ，n=0，1，…，N,τ=T/N，其中τ為時間步長。

對于 0＜γ＜1，引入記號…，在t=tn+1時間點離散各項，利用[3]

得到下面格式：

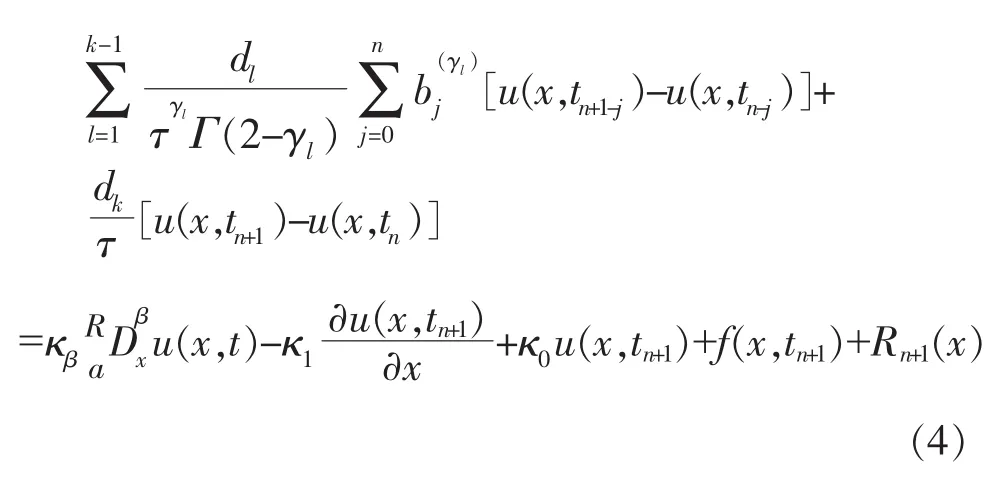
其中

以及

其中C為正的常數。

經整理，（4）式可改寫為

令 un=un（x）為 u（x，tn）的數值近似，fn=fn（x）表示f（x，tn），略去誤差項 τRn+1（x），可得到半離散格式：

1.2 多項式點插值

接下來介紹本文用到的離散空間變量的多項式點插值。

首先，在問題域[a，b]內生成場節點，節點可以隨機生成，也可以人工加入節點。設有內部節點x1,x2,…xM-1,和邊界節點 x0，xM。

對每一個場節點，都做一個包含該節點的支持域，在實際計算中，一般取節點平均間距的二到三倍大小[11]。

設第i個節點xi的支持域為Ωi，支持域Ωi內包含 mi個節點 xi1，xi2，ximi。為書寫方便起見，記Di={i1,i2,…，imi}，這就意味著，當 l∈ Di時，xl∈ Ωi。

接下來，在節點的支持域內對函數u（x）利用基函數進行逼近。為了描述方便，假設計算點的支持域內包含m個場節點x1,x2,…,xm，連續函數u（x）可以近似表示為：

其中pj（x）為空間坐標變量的單項式，被稱為多項式基，m是多項式基的個數，a=[a1,a2,…am]T,aj為待定常數。一般地，可取一維的m-1次完備多項式為

為了確定待定系數 aj（j=1,2,… ,m ），令（i=1,2,… ,m ），即

寫成矩陣形式為

其中 Us=[u（x1）u（x2）… [u（xm）]是節點上的函數值向量，以及

由于x1,x2,…,xm互不相等，則矩陣Pm是m階可逆方陣.由(11)，有：

將（12）代入（9）,可得

其中 ΦT（x）是形函數向量，其定義為

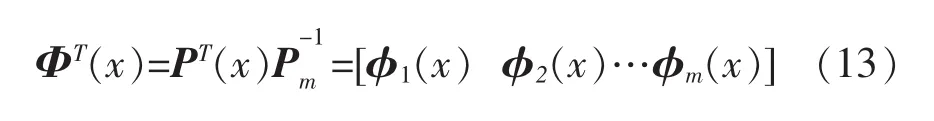
容易得到，形函數向量ΦT（x）的k階(k為正整數)導數為

形函數向量ΦT（x）的β階 (β為正實數)左側Riemann-Liouville導數為：

于是，我們有

1.3 全離散格式

接下來，我們將對方程（8）進行空間離散。

考慮內部節點 xi（i=1,2,… ,m ），每個節點 xi對應的支持域為 Ωi，支持域 Ωi內包含 mi個節點 xi1，xi2，ximi，

為方便起見，記假設方程（8）的近似解為

將該式代入方程（8），并令 x=xi，于是，可得

邊界條件為

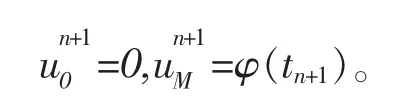
由冪函數的分數階導數公式[10]：

得到(14)式中形函數 φj（x）（j=1,2,… ,n）在 xi的分數階導數表達式為：

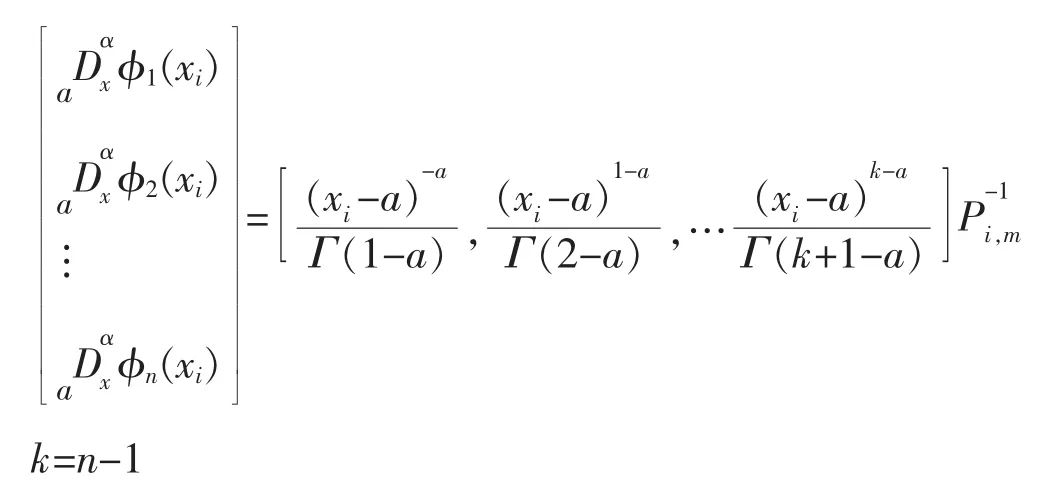
其中 Pi，m為節點 xi的支持域｛xl，l=i1，i2，… ,in｝形成的方陣，

2 數值結果

為了避免在計算中產生Runge現象，在構造場節點時選擇6個臨近節點作為局部支持域時k=5，此時，基函數為5次完備多項式基。

例1考慮下列方程：

帶有邊值條件

以及初始條件：

其中

該方程的精確解為 u（x，t）=x2t2。

首先，將問題域[0,1]用規則節點 xi=ih（i=0，1，2，…，100）劃分，采用全離散格式(14)進行求解（計算中取m=5），從圖1看出，精確解和數值解吻合得很好。

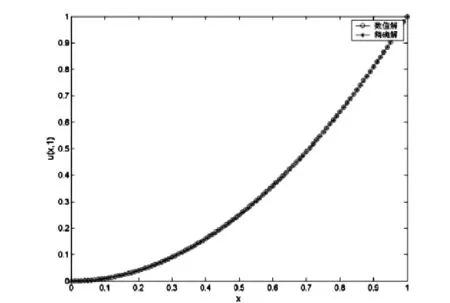
圖1 規則點劃分的數值解與精確解Figure 1 Numerical and exact solutions for regular distributed nodes

表1中列出時間步長變化時，數值解與精確解的誤差以及誤差階。

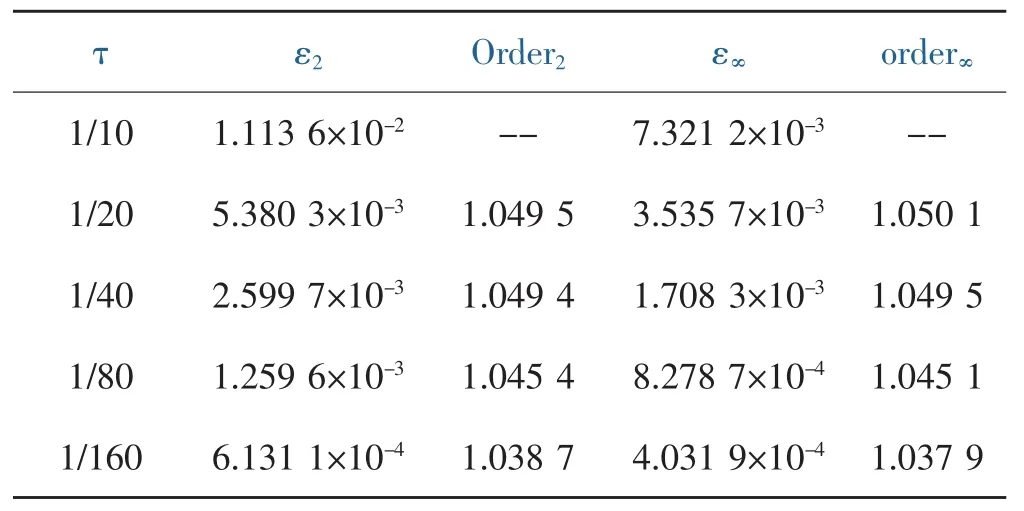
表1 采用規則點劃分求解的數值解與精確解的誤差以及誤差階Table 1 Error of the numerical and exact solutions for regular distributed nodes

接下來將問題域用不規則節點劃分，采用全離散格式(14)進行求解。圖2給出此時精確解與數值解。

圖2 不規則點劃分的數值解與精確解Figure 2 Numerical and exact solutions for irregular distributed nodes

表2列出針對不規則點劃分空間變量，時間步長變化時，數值解與精確解的誤差以及誤差階。由此看出，本節提出的數值方法仍然適用于不規則點劃分。

表2 采用不規則點劃分求得的數值解與精確解的誤差以及誤差階Table 2 Error of the numerical and exact solutions for irregular distributed nodes

例2考慮下列時間-空間分數階微分方程

帶有邊值條件

以及初始條件

其中 γ1=0.9，γ2=0.6，β=1.8，且

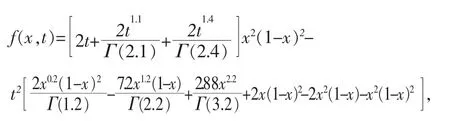
該問題的精確解為 u（x，t）=t2x2（1-x）2。

同樣，將問題域[0，1]分別用等距節點劃分以及非等距節點劃分，采用全離散格式(14)進行求解。從圖3和4看出，無論是規則點，還是不等距節點，精確解和數值解吻合得很好。

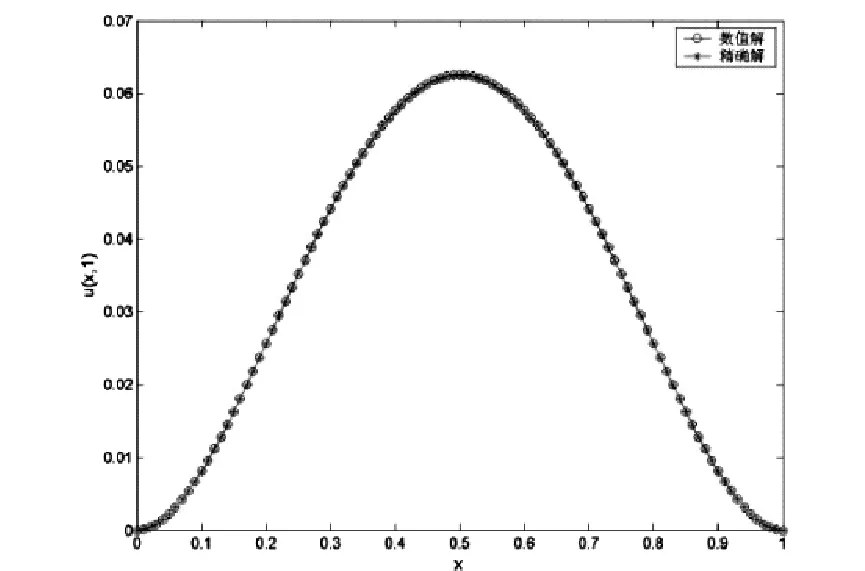
圖3 規則點劃分時的數值解與精確解Figure 3 Numerical and exact solutions for regular distributed nodes

圖4 非等距節點劃分時的數值解與精確解Figure 4 Numerical and exact solutions for irregular distributed nodes

表3和4中給出規則點和不規則點劃分空間變量，時間步長變化時的誤差以及誤差階。

表3 規則點劃分時求得的數值解與精確解的誤差以及誤差階Table 3 Error of the numerical and exact solutions for regular distributed nodes

表4 非等距節點劃分時求得的數值解與精確解的誤差以及誤差階Table 4 Error of the numerical and exact solutions for irregular distributed nodes

[1]DENTZ M,BERKOWIZ B.Transport behavior of a passive solute in continuous time random walks and multirate mass transfer[J].Water Resources Research,2003,39(5)：1111-1130.

[2]HARVEY C,GORELICK S.M.Rate-limited mass transer or macrodispersion：Which dominates plume evolution at the Macrodispersion Experiment (MADE)site [J].Water Resources Research,2000,36(3)：637-650.

[3]SUN Z Z,WU X N.A fully discrete difference scheme for a diffusion-wave system[J].Apply Numerical Mathematics,2006(56)：193–209.

[4]ZHANG Y,MEERSCHAERT M M,BAEUMER B.Particle tracking for time-fractional diffusion[J].Physical Review E,2008(78)：036705.

[5]MEERSCHAERT M M,ZHANG Y,BAEUMER B.Particle tracking for fractional diffusion with two time scales[J].Computers and Mathematics with Applications,2010(59)：1078-1086.

[6]ZHUANG P,LIU F,ANH V,et al.New solution and analytical techniques of the implicit numerical method for the anomaloussubdiffusion equation[J].Siam Journal on Numerical Analysis,2008,46(2)：1079-1095.

[7]LIU Q,LIU F,TURNER I,et al.Numerical simulation for the 3D seepage flow with fractional derivatives in porous media[J].Ima Journal of Applied Mathematics,2008,74(2)：201-229(29).

[8]LI C,ZENG F.Finite difference methods for fractional differential equations[J].International Journal of Bifurcation and Chaos,2012,22(4)：1230014.

[9]LI C,DENG W H,SHEN X Q.Exact Solutions and Their Asymptotic Behaviors for the Averaged Generalized Fractional Elastic Models[J].Communications in Theoretical Physics,2014,62(4)：443-450.

[10]PODLUBNY.Fractional differential equations[M].Salt Lake：Academic Press,1999.

[11]LIU G R.Mesh free methods：moving beyond the finite element method[M].Boca Raton：CRCPress,2005.