IBC代數的性質及等價刻畫

王 序

?

IBC代數的性質及等價刻畫

王 序

江南大學理學院, 江蘇 無錫 214122

本文采用IMV代數的構造方法，定義了IBC代數，對其相關性質進行了初步研究，進而在其上定義了偏序關系，給出了IBC代數的一種構造方法，并給出了IBC代數的等價公理系統。

Basic代數; MV代數; IMV代數; IBC代數

Basic代數是Chajda I為了研究MV代數和正交模格的共性而引入的代數結構[1],它在多值邏輯和量子力學中有著十分重要的作用.到目前為止,關于Basic代數的性質與結構已有多人討論[2-7].2014年,Cabrera LM和Mundici D以MV代數的區間為模型,抽象地提出了區間MV代數的(簡稱IMV代數)概念,證明了IMV代數與MV代數是范疇等價的,并給出自由IMV代數的表示[8].由于Basic代數是MV代數的推廣,因此有必要將Cabrera LM和Mundici D的思想推廣到Basic代數.本文采用IMV代數的構造方法,定義了IBC代數,對其相關性質進行了初步研究,在其上定義了偏序關系,給出了IBC代數的一種構造方法,并給出了IBC代數的等價公理系統.

1 預備知識

定義1.1[1](2,1,0,0)型代數=(,+,?,0,1)稱為Basic代數,如果它滿足下列條件:

(1)+0=;

(2)??=;

(3)?(?+)+=?(?+)+;

(4)?(?(?(+)+)+)+(+)=1.

設為Basic代數,稱為可換的,若+=+稱為可結合的,若(+)+=+(+).

文獻[1]證明了(,≤,0,1)是帶有最大元1和最小元0的有界格，且對任意的,?,?=?(?+)+,?=?(???).

引理1.1[1]設是Basic代數,則下列性質成立:

(1) 0+=; (2)?+=+?=1; (3)+1=1+=1; (4) 若可交換,則+(?)=(+)?(+),+(?)=(+)?(+).

定義1.2[8](2,2,1,1,0,0,0)型代數=(,0,1,,?,D,?,?,?)稱為IMV代數,如果它滿足下列條件:

(1)?(?)=(?)?;

(2)?=?;

(3)?0=;

(4)??0=?0;

(5)??=;

(6)?=?(???);

(7) 1=?0;

(8)?=?D?;

(9)?=;

(10)D0=0;

(11)D1=1;

(12)D=0;

(13)DD=D;

(14)D?=?;

(15)D(?)=D?D;

(16)D(?)=D?D;

(17)D???=1;

(18) (????D)?D=;

(19)?(?D?D)?D=?(?D?D)?D.

2 IBC代數的定義及性質

本節采用IMV代數的構造方法,定義了IBC代數,對其相關性質進行了初步研究,在其上定義了偏序關系,并給出了IBC代數的一種構造方法.

定義2.1 (2,1,1,1,0,0,0)型代數=(,0,1,,?,D,?,?)稱為IBC代數,如果它滿足下列條件:

(1)?0=; (2)??=; (3)?=; (4)D=0; (5)D?=?; (6)D(?)=D?D(7)?D??=1; (8)?(????D)?D=; (9)?(?D?D)?D=?(?D?D)?D; (10)?(?(?(D?D)?D)?D)?(D?D)=1.

其中1=?0,D=?D?.

下述例子表明IBC代數是存在的.

例2.1設={0,1,},在上定義運算?,D,?,和?如下:

x?xxDxx?x?0i1 01000000i1 iii0i1iii1 1011111111

容易驗證,=(,0,1,,?,D,?,?)是一個IBC代數.

定理2.1設是區間Basic代數,對任意的,,?,下列性質成立:

(1)?=1; (2)D1=1,?0=0; (3)D0=0,?=1; (4)D=???; (5)?(????)??=?(????)??

(6)?(?(?(???)??)??)?(???)=1 (7)?=D,DD=D,??=?(8)D?1=1, 1?D=1, 1??=1 (9) 0?D=D, 0??=?(10)D?D??D1???????1 (10) 若D=D,?=?, 則=; (11)?1=1?=1.

證明：(1) 由定義2.1，?=?D?=?D=?0=1;

(2) 由(1)及定義2.3，D1=D?=?=1,?0=?D?0=?D1=?1=0;由(2)及定義2.3,D0=??D0=?(?D0?0)=?(?D0??0)=?1=0, 再由定義2.3,?1=?D?1=?D0=?0=1;

(3) —(6)由定義2.3可得;

(7)?D=?D?(D)=?D?D??=?D(?D??)=?D??=???D.另一方面,DD=D(?D)=D?(D)=?D=D同理可證?=D?=?(D?)=??;

(8)D?1=??D?1=(?(?D?0)?0)?1=?(?(?(?D0?)?D)?D0?(?D0?D0)=1,同理可證,??1=1;1?D=?(?(?(D?1)?1)?0)?(D?0)=1,同理可證,1??=1;

(9)D=??D=?(?D?D0)?D0=?(?0?D)?D=?1?D=0?D,同理可證,?=0??;

(10)?D?D=?(?D1?D)?D=?(?D?D1?D1=?(?D?1)?1=1,由定義2.1,1=??D??D=D??D,故?D?D=D??D=1.同理可證,?D??=????=1;

(11) 若D=D,?=?,則由定義2.3,=?(????D)?D=?(????D)?D=.

?D?D=?(?D?D)?(?D?D)=?(?(?(?D?D)?D)?D)?(?D?D)=1

????=?(????)?(????)=?(?(?(????)??)??)?(????)=1

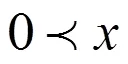
下面我們給出由Basic代數構造IBC代數的方法,建立Basic代數和IBC代數之間的橋梁.

定理2.3設=(,+,',0,1)是Basic代數,取使得對任意的?,≠.令=è{}。在上定義運算?,?,D如下:對任意的,?

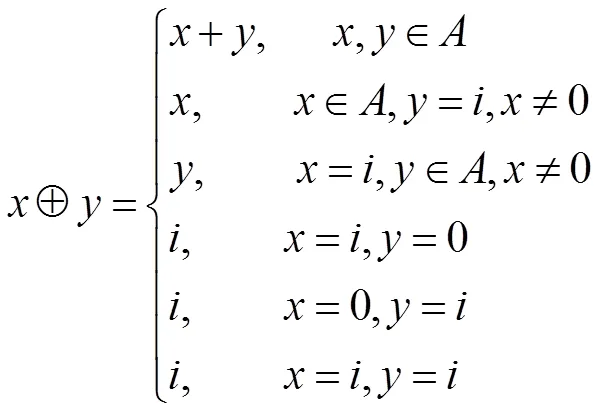
則=(,?,?,D,?,0,1,)是區間Basic代數.

證明:由定義2.3,只需證明等式(IB-1)-(IB-10)成立.由?,?,D定義,等式(IB-1)-(IB-5)成立.下面證明(IB-6)-(IB-10)成立.

(IB-6)對任意的,?,

1) 若,?,則?=+?,從而由D及?的定義得D(?)=+=D?D.

2) 若=,?,≠0,則?=,D=0,D=,于是D(?)=D(?)==D?D.

3) 若=,?,≠0,同理可證D(?)=D?D.

4) 若=,=0,則D(?)=D(?0)=D=0,D?D0=0?0=0.于是D(?)=D?D.

5) 若=0,=,同理可證D(?)=D?D.

6) 若==,則D(?)=D(?)=D=0=D?D.

所以,(IB-6)成立.

(IB-7)對任意的?,若?,則D=?=,故?D??=?+='+=1.若=1,則?D??=?D??=?0?1=1+1=1.因此,(IB-7)成立.

(IB-8)對任意?,若?,則?(????D)?D=?(???)?=?(?'?)?=?('+)?=?1?=.若=,則?(????D)?D=?(??1?0)?0=??0=.因此,(IB-8)成立.

(IB-9)對任意的,?,由D定義知D,D?.所以由定義2.1,?和?的定義知(IB-9)成立.

(IB-10)同(IB-9)可證.

綜上可知,=(,?,?,D,?,0,1,)是區間Basic代數.

3 IBC代數的等價公理系統

本節利用→算子給出了IBC代數的等價公理系統.

引理3.1設=(,0,1,,?,D,?,?)是IBC代數，在上定義→=??,對",,?,滿足下列條件:

(1)?→D=

(2)??=

(3) (D→D)→D=(D→D)→D

(4)?=

(5)D?D?=?D?

(6)D(?→)=?D→D

(7)D→?D?=?D

(8) (((?D→D)→D)→D)→(?D→D)=?D

(9) (?(→D?)→D→D=

(10) (?D?→?D?)→?D?D=(?D?→?D?)→?D?

(11) (((D?→?D?)→?D?)→?D?)→(D?→?D?)=?D

(12)?D→D=D,?D→??D?=?D?

(10)D→D=?D,?D?→?D?=?D

(11)D→=?→?D=?D

證明:由IBC代數的定義及定理2.1容易證明.

定理3.1設(0,1,1,2)型代數=(,,?,D,→)滿足引理3.1中的(1)-(9),=(,0,1,1,,?,D,?,?)是IBC代數，則代數=(,,?,D,→)與=(,0,1,,?,D,?,?)等價.

證明:設=(,0,1,,?,D,?,?)是IBC代數，在上定義→=??,由引理3.1可知,是代數=(,,?,D,→).

反之,設代數=(,,?,D,→)滿足引理3.1中的(1)-(9)，在上定義0=D,1=?D,?=?D?,?=?→,對",,?,我們來逐條驗證定義2.1中的條件:

(1)?0=?→0=?→D=

(2)??=

(3)?(?D?D)?D=(D→D)→D=(D→D)→D=?(?D?D)?D

(4)?=

(5)D=0

(6)D?=D?D?=?D?=?

(7)D(?)=D(?→)=?D→D=D?D

(8)?D??=?D??D?=D→?D?=?D=1

(9)?(?(?(D?D)?D)?D?(D?D)=(((?D→D)→D)→D)→(?D→D)=?D=1

(10)?(????D)=?(?D??D)?D=(?(→D?)→D→D=

因此,代數=(,0,1,,?,D,?,?)是IBC代數.

綜上所述,IBC代數=(,0,1,,?,D,?,?)與滿足定理2中條件(1)-(9)的代數=(,,?,D,→)等價.

4 總結

Basic代數在多值邏輯和量子力學中有著十分重要的作用,我們采用IMV代數的定義方法,對其相關性質進行了初步研究,在其上定義了偏序關系,給出了IBC代數的一種構造方法,并利用→算子給出了IBC代數的等價公理系統.

[1] Chajda I, Halas R, Kuhr J. Many-valued quantum algebras[J]. Algebra Universalis, 2009,60(1):63-90

[2] Chajda I, Kolarik M. Independence of axiom system of basic algebras[J]. Soft Computing, 2009,13(1):41-43

[3] Chajda I, Kuhr J. Ideals and congruences of basic algebras[J]. Soft Computing, 2013,17(3):401-410

[4] Botur M, Halas R. Commutative basic algebras and non-associative fuzzy logics[J]. Archive for Mathematical Logic, 2009,48(3):243-255

[5] Botur M. An example of a commutative basic algebra which is not an MV-algebra[J]. Mathematica Slovaca, 2010,60(2):171-178

[6] Botur M, Halas R, Kuhr J. States on commutative basic algebras[J]. Fuzzy Set and Systems, 2012,187(1):77-89

[7] Botur M, Halas R. Complete Commutative Basic Algebras[J]. Order, 2007,24(2):89-105

[8] Cabrer LM, Mundici D. Interval MV-algebras and generalizations[J]. International Journal of Approximate Reasoning, 2014,55(8):1623-1642

The Properties and Equivalent Characterization of IBC Algebras

WANG Xu

214122,

In this paper, we used the construction method of IMV algebra to define the IBC algebra and do the preliminary research on its related properties, and then define partial ordering relation on it to give a construction method of IBC algebra and the equivalent axiom system of IBC algebra.

Basic algebras; MV algebras; IMV algebra; IBC algebra

O144.1;O159

A

1000-2324(2018)03-0539-04

2017-01-02

2017-03-03

王序(1993-),女,碩士研究生,研究方向:多值邏輯與模糊邏輯. E-mail:ilove507@yeah.net