巧用“數學計算模型”計算20以內退位減法
新疆生產建設兵團第三師圖木舒克市49團第一中學 趙 燁
筆者從教二十多年,一直以來都是教高年級數學,今年是第一次教一年級。在教學數數以及十以內加減法的內容時,學生都能輕松愉快地學習并掌握這些知識,可是對于20以內退位減法內容的學習、師生都下了很大功夫、收效還是不盡如人意。我又去問那些曾經教過一年級數學的老師,他們也說教學這塊內容時,確實下了很大力氣,但都沒收到滿意的效果。在計算20以內退位減法時,理論上學生都能背得爛熟(當個位不夠減時,從十位退一、在個位上加十再減)。可是在實踐運用時,學生每做一道題都要把退位減法的計算法則背一遍,這樣學生做得又慢,錯誤率又高。但筆者在課堂上發現,一年級的孩子,喜歡獲得直觀性知識經驗。于是積極引導學生去進行抽象、概括,建立數學模型,探求問題解決的方法,使學生進一步體驗數學建模思想與方法。教學中,筆者始終堅持以學生發展為本的新理念,依據教材內容和學生的年齡特征,在課堂教學中和學生一起大膽實踐、探索,通過觀察、實驗、分析等活動,終于發現并建立了20以內退位減法的計算模型,培養了學生解決問題的能力,增強學生的探究能力和創新意識。由原來學生厭煩的枯燥的理論說教轉變成學生喜聞樂見的直觀計算模型,孩子們利用自己發現并建立的計算模型很快學會了20以內退位減法的計算。現把我們的發現與大家一起分享,希望這一“模型計算法”能給曾經為學習退位減法的計算而犯難的師生們提供一種新的思想,一種新的方法。
數學“模型”計算法,它的算理仍舊是“破十法”。比如13-9,因為13是由一個10和一個3組成的,可以先用10減9,剩下的1和個位上的3合在一起就是4,所以13-9=4,但這是純理論的東西,學生不容易理解也不喜歡接受。我們通過觀察、實驗、分析等活動,建立了20以內退位減法的計算模型、就能把這種理論變成直觀的模型,學生看得懂,就學得會了。
首先以十幾減9為例吧:在計算十幾減9時,當個位不夠減時,首先從十位退1(即10),用10-9=1,把這個1加在被減數的個位上,就是得數。請看下面十幾減9的計算模型:
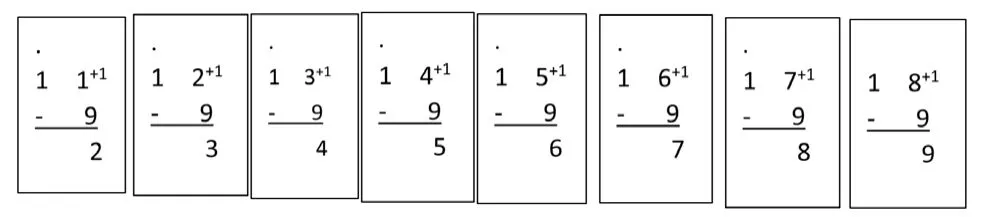
在計算十幾減8時,算理同十幾減9,當個位不夠減時,先從十位退1(即10),用10-8=2,這個2加在被減數的個位上,就是得數。計算十幾減8的模型:

同樣的道理計算十幾減7時,當個位不夠減時,先從十位退一(即10),用10-7=3,這個3加在被減數的個位上,就是得數,計算十幾減7的計算模型:
同樣的道理建立以十幾減6的計算模型:

再比如下面的十幾減5的模型:

同理,利用“破十法”的減法算理還可以建立十幾減4的計算模型、十幾減3的計算模型……只要是20以內退位減都可以應運這種模型來進行計算。學生都能通過觀察這個算式模型迅速而又準確地算出得數。這種計算方法不但適用于20以內退位減法,也可以推廣到其他數位的退位減法上,只要能把這種計算方法掌握,就能大大提高同學們的計算速度和正確率。
數學建模思想是一種新的教學思想和教學手段,通過建模,把無形的抽象的理論轉化成一種有“型”的“模子”。讓學生在觀察中發現、在觀察中感悟、在觀察中得出結論,既激發了學生的學習興趣,又培養了學生愛動腦,愛思考,愛觀察,愛發現的好習慣,同時也培養了學生解決問題的能力。
我們師生在學習實踐中發現并建立的20以內退位減法計算模型給我們的教學和學習帶來很大幫助,希望我們的這種模型計算法能得以推廣,使更多師生掌握并應用。

