基于PIPs樣本優化的機車車輛軸溫實時預測方法

楊則云

?

基于PIPs樣本優化的機車車輛軸溫實時預測方法

楊則云

（中車青島四方機車車輛股份有限公司，山東 青島 266111）

建立了一種基于最小二乘曲線擬合的軸溫預測模型，并采用PIPs對樣本進行優化改進，提高了預測精度。首先基于PIPs對建模樣本點進行優化選擇，選取歷史溫度數據中能表征溫度變化趨勢的重要點作為建模樣本點，再利用最小二乘曲線擬合法建立實時溫度預測模型對機車車輛軸承溫度進行實時預測。以某型機車車輛履歷軸承溫度數據為例，采用本文模型對任意時刻溫度的后5分鐘溫度進行預測，將預測結果與實際監測結果進行連續對比，驗證了所建立的軸溫預測模型及其改進模型的有效性：基于最小二乘曲線擬合預測模型的綜合平均相對誤差為3.47%，綜合最大相對誤差為20.27%，而進行PIPs改進后的綜合平均相對誤差為2.67%，同比降低了23.05%，綜合最大相對誤差為16.67%，同比降低了17.76%。

軸承溫度；時間序列；曲線擬合；PIPs

熱軸、燃軸是危及鐵路運輸安全的嚴重故障，表現為運行中軸承異常高熱，輕則造成緊急停車導致經濟損失，重則引發列車脫軌危及旅客生命安全。目前，由車軸異常發熱引發的事故時有發生。溫度是反映軸承熱狀態的最直接參量，溫度突然升高或超過警戒值，是軸承異常運行和發生故障的重要信號。軸承磨損退化可能造成軸溫升高，而正常工況下軸承轉速、載荷、環境溫度的變化亦可引起軸承溫升[1]。軸承溫升原因的不確定性[2-3]是基于溫度信號進行故障診斷的難點。現有軸溫監測系統預警規則根據絕對閾值進行報警，誤報漏報現象頻發且在溫度達到閾值后再進行預警剩余處置時間不足。因此對車輛軸溫進行實時預測，掌握軸溫未來變化趨勢，提前預警以便及時調整行車策略，具有重要意義。

為滿足車輛軸承溫度實時準確預測的要求，將軸承溫度預測問題轉化為基于軸承歷史溫度數據的時間序列預測問題。在軸承溫度預測問題研究上，Han[4]等針對水電機組軸承的故障預測問題，采用自回歸滑動平均模型（ARMA）對溫升趨勢進行預測，該模型只適用于線性系統的預測且不適用于長期預測，對機車車輛軸溫這樣的動態過程預測精度不足。文獻[5-7]分別基于新陳代謝灰色模型、GA-BP融合算法、廣義隱馬爾可夫模型對軸承溫升進行預測，但這些方法都只能進行短時預測，不能滿足機車車輛軸溫實時預測的要求。

曲線擬合可以直接通過最小二乘法估計模型參數來對函數近似，算法原理簡單，不需要進行參數優化，并且實施方便、時間復雜度低，是一種典型的趨勢預測方法。但在基于最小二乘曲線擬合的軸承溫度預測中，由于歷史溫度數據呈現波動變化且存在噪點，建立的預測模型不能準確描述溫度變化趨勢，導致預測誤差較大，針對這一問題本文提出結合PIPS[6]（Perceptually Important Points）樣本優化的曲線擬合軸溫預測方法。

1 PIPs算法和最小二乘曲線擬合預測算法

1.1 PIPs算法

時間序列由一系列的點構成，每個數據點的幅值對時間序列波形有不同程度的影響，序列中的少數點即可確定其波形，而序列中的剩余點可被忽略，PIPs由Chung，Fu等人[8]于2001年提出，用于尋找價格序列中的特征點，在數據挖掘中PIPs作為一種動態分割方法主要用于時間序列的表達，定義時間序列中的重要點，去除了序列中的波動點及噪聲點的干擾，將時間序列非等間距地表出，準確表達了時間序列的變化趨勢。

PIPs算法流程如圖1所示，首先通過構造PIPs定義序列中的重要點，以序列起始點與最末點作為初始的兩個PIPs，并計算序列中其余點與已定義PIPs距離，將距離最大的點定義為下一個PIPs，重復迭代這一過程，直至PIPs數量達到用戶定義數量。用非等間距的PIPs對原序列進行重新表出。

圖1 PIPs算法流程

1.2 基于最小二乘曲線擬合的預測算法

曲線擬合函數一般采用如下所示廣義多項式線性模型：

式中：1，2，...，θ是模型的個參數；為模型自變量；（）為基函數。

對于給定組離散觀測序列{x， y}，＝1，2，...，，模型可表示為：

則模型可寫成向量形式＝，將擬合值與實際值的離差平方和作為曲線擬合精度指標：

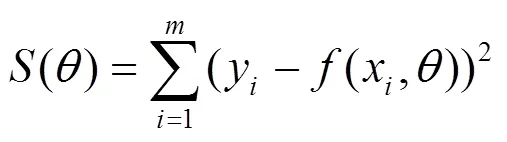
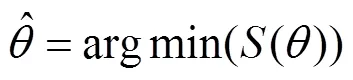
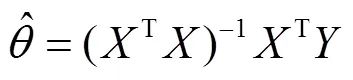
由曲線擬合原理可知，基函數的應用可以增加擬合模型的非線性能力，從而實現對曲線函數的逼近。不同的基函數對不同形狀特點的曲線的逼近能力也不盡相同，所以基函數的選擇對曲線擬合的精度有著直接影響。本文通過分析對比，選擇冪函數作為曲線擬合的基函數。工程應用中常見的基函數有多項式模型、指數模型、冪函數模型。

多項式模型為：

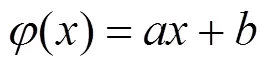
指數模型為：

冪函數模型為：

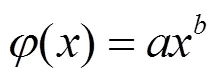
2 基于PIPs建模樣本優化的軸溫預測方法

軸溫序列屬于一種非平穩非線性的時間序列，容易受環境溫度、運行線路、運行速度等因數的影響。如果利用所有前序軸溫樣本數據進行建模，其中所包含的噪聲點會對模型預測結果造成較大的影響，本文采用的算法首先對歷史軸溫窗口內的軸溫數據運用PIPs算法進行篩選后再構造樣本空間，在降低時間序列維度和抑制噪聲的同時，對重要的點也不會造成扭曲，保持了原始數據的準確性，實現了建模樣本點的優化選擇。再采用曲線擬合的方法構建預測模型，利用最小二乘法求解模型參數，輸出預測曲線。最后綜合考慮軸溫變化趨勢，根據預測曲線制定合理及時的預警策略。算法具體步驟如圖2所示。

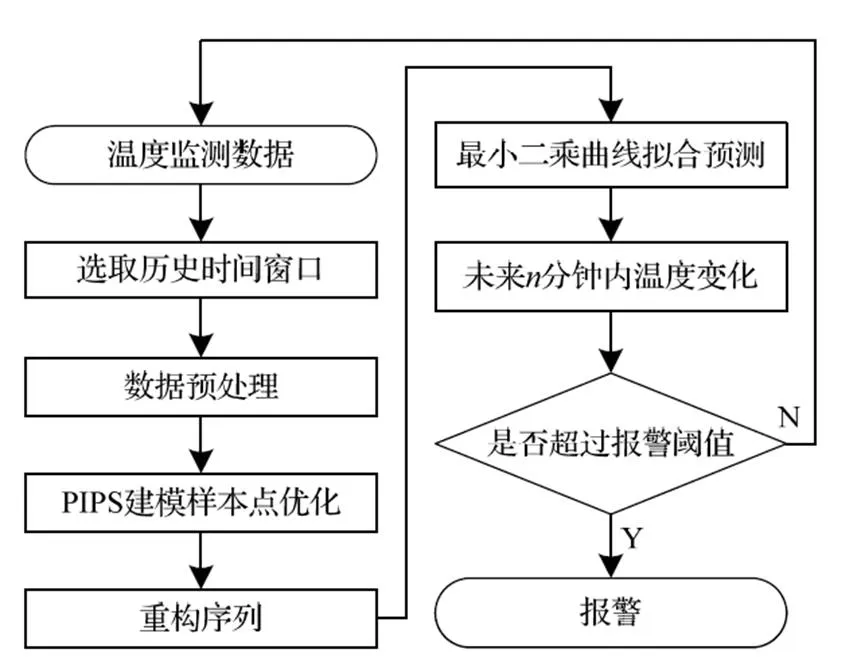
圖2 基于PIPs建模樣本優化的軸溫預測預警流程

（1）通過插值對數據中的缺失點進行預處理。基于當前時刻的軸溫序列，在其歷史時間鄰域內取一段長度為的歷史軸溫序列：

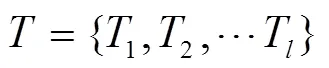
（2）定義重要程度相鄰的兩個點PIPS為χ＝{T，}和χ+T＝{T+T，+}，則下一個重要點為距離χ、χ+T最近的點，距離為：

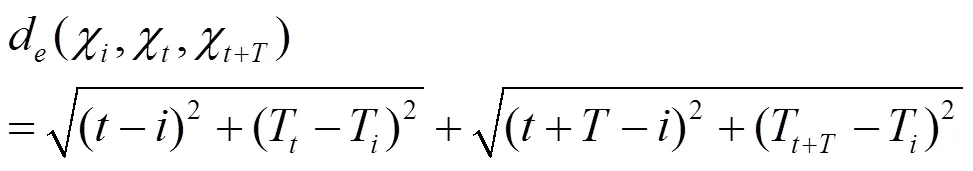
將溫度序列的首尾兩點初始化為最開始的兩個PIPS，重復迭代計算即可得到所有的PIPS。

（3）按照重要程度對歷史數據點進行篩選，重構為一段長度為的溫度序列T，其對應的時間坐標序列為。

（4）構造曲線擬合模型，擬合基函數為冪函數（），擬合函數模型可用表示為：

（5）將重構后的實際監測數據{t，T}（＝1，2，...，）代入曲線擬合模型岢，可得：

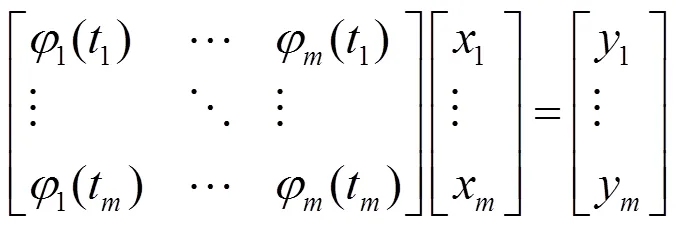
將其向量化可得：

則軸溫預測模型估計參數為：

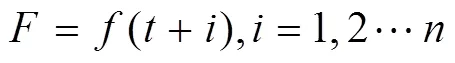
3 實例驗證

3.1 實驗條件

以某型機車車輛履歷服役軸溫監測數據為例，數據來源為某型機車車輛車載軸溫監測系統測得的同列車上多個軸溫測點溫度，溫度傳感器為pt100，采樣頻率為1 Hz，監測軸溫數據傳輸頻率為每分鐘一次。按每分鐘一次的頻率取1 min內測點溫度最大值對實測溫度值進行重采樣，以齒輪箱相關軸承溫度測點如表所示履歷軸溫數據進行驗證，其位置分布如圖3所示測點。選擇相同的歷史數據窗口預測后序5 min溫度變化情況，分別用本文提出的基于PIPs建模樣本點優化的曲線擬合法與曲線擬合法進行對比。

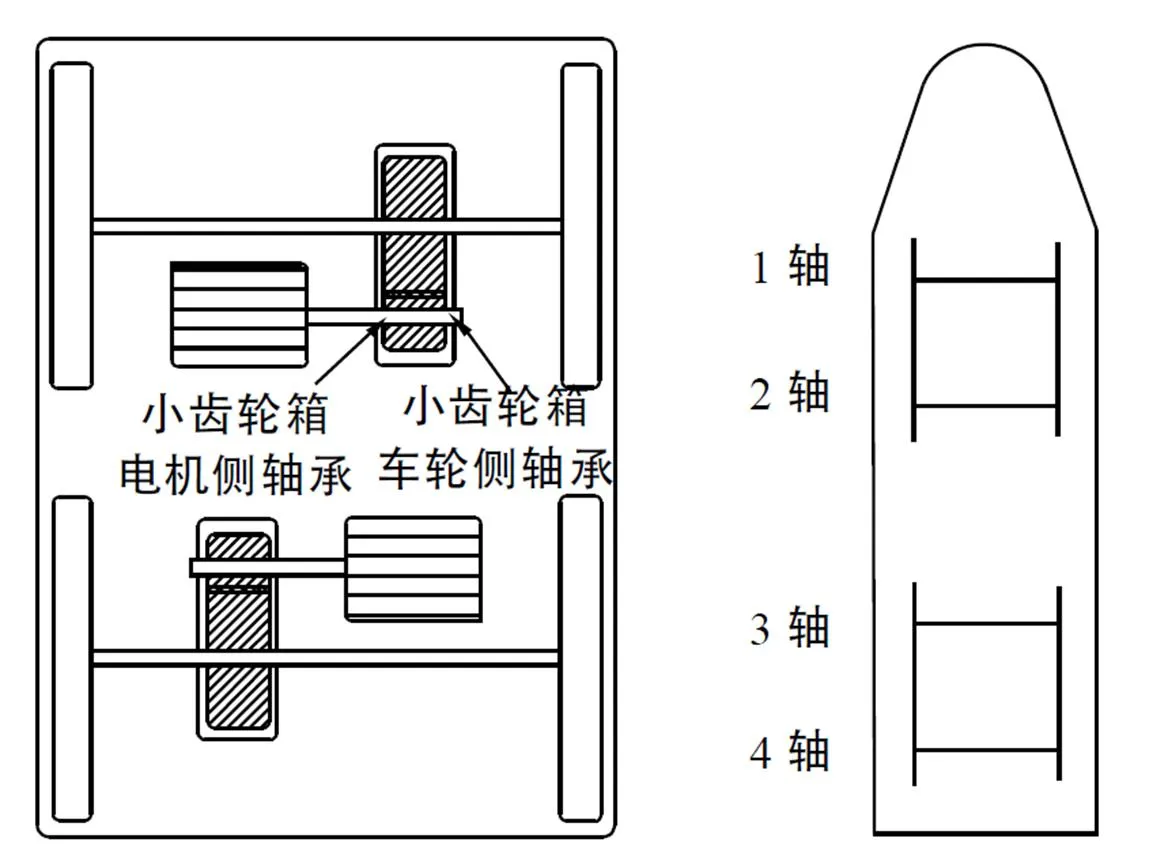
圖3 機車車輛軸承位置分布

表1 軸溫測點位置及通道編號

3.2 驗證結果及分析

在當前主流的計算機配置條件下，每測點進行一次預測的運行時間約為30 ms，可以滿足在線預測的實時性要求。基于本文模型和上述實驗條件進行的5 min后續軸溫的預測結果如表2所示。

表2和表3分別為改進前后兩種方法的誤差統計情況，表中各種誤差的計算方法為（逐點對比預測值和實測值，時間間隔為1分鐘）：

絕對誤差＝|預測值－實測值|；

相對誤差＝絕對誤差/實測值；

平均絕對誤差＝Σ（絕對誤差）/總分鐘數；

平均相對誤差＝Σ（相對誤差）/總分鐘數；

最大絕對誤差＝Max（相對絕差）；

最大相對誤差＝Max（相對誤差）。

對算法的評價采用綜合平均相對誤差和綜合最大相對誤差。其計算方法為：

綜合平均相對誤差＝Σ（各通道的平均相對誤差）/通道數；

綜合最大相對誤差＝Max（各通道的最大相對誤差）。

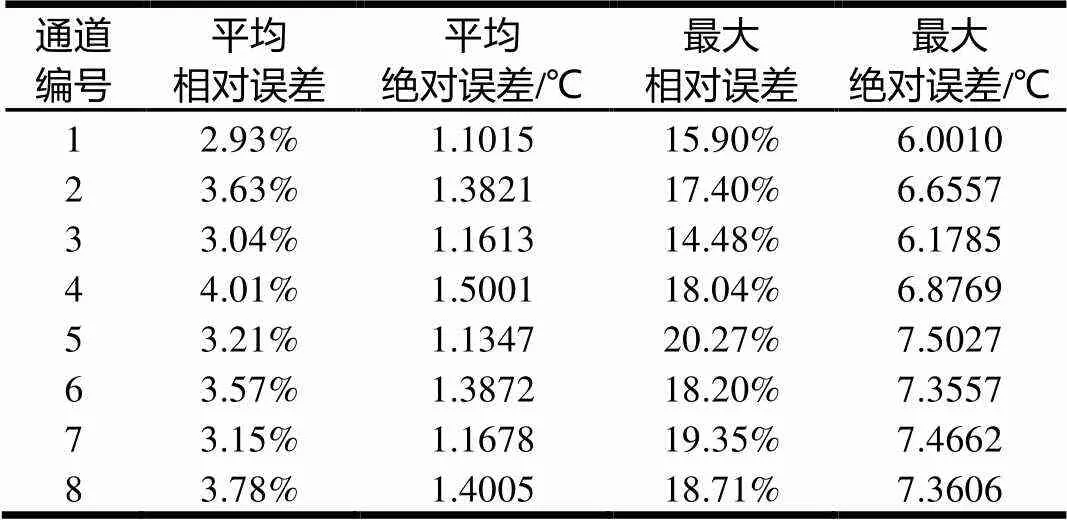
表2 基于最小二乘曲線擬合預測模型的預測誤差

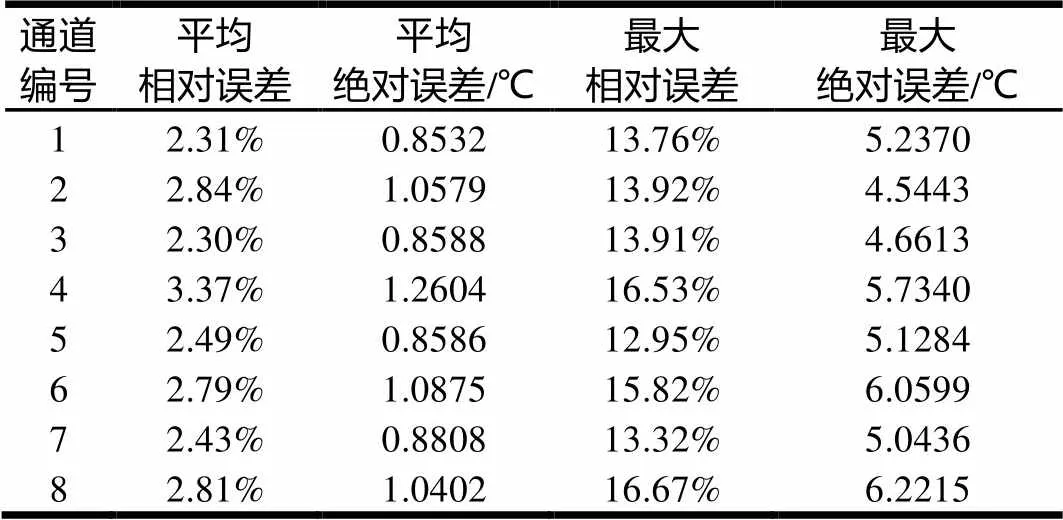
表3 基于PIPs對建模樣本優化改進后的預測誤差

從公式可以看出，綜合平均相對誤差可以反映出算法對于所以通道的適應性和預測準確度，而綜合相對最大誤差可以反映出預測值和實際值的偏離程度，因此選其作為評價指標。

從表2和表3中可以看出，基于最小二乘曲線擬合模型的預測綜合平均相對誤差為3.47%；綜合最大相對誤差為20.27%。進行PIPs樣本優化后的預測模型的綜合平均相對誤差為2.67%，同比降低23.05%；綜合最大相對誤差為16.67%，同比降低17.76%。

表4為基于PIPs建模樣本優化后的誤差相比優化前的降低率，計算方法為：

預測誤差降低率＝（改進前預測誤差－改進后預測誤差）/改進前預測誤差。

通過表4可以發現，從各通道的平均相對誤差降低率看，改進后的模型對于各通道的預測誤差率都有15%以上幅度的降低，從最大相對誤差降低率看，改進后的模型對于各通道的預測誤差率降低率也比較顯著，最高達到36.11%。

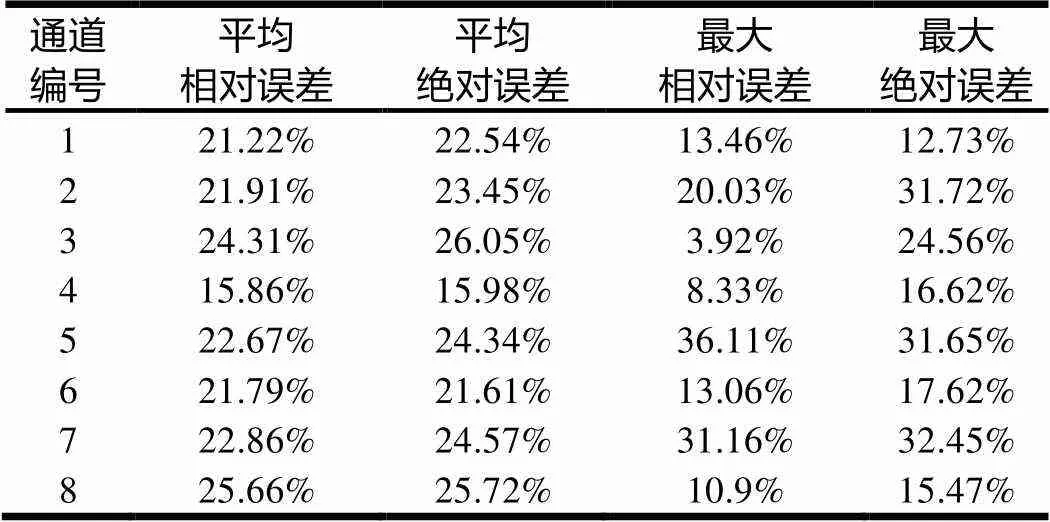
表4 優化后比優化前預測誤差降低率

以綜合改進效果比較明顯的通道5為例，其實測值、基于最小二乘曲線擬合模型的預測值、PIPs樣本優化后的預測值如圖4所示。

圖4 改進前后1軸小齒輪箱車輪（5通道）側軸承預測曲線

4 小結

針對基于最小二乘曲線擬合的機車車輛軸承溫度在途預測中存在的預測誤差較大問題，本文結合PIPs方法進行建模樣本優化選擇，選取序列中重要點對歷史軸承溫度序列進行重新表出，去除序列波動，噪聲點的影響，準確描述溫度變化趨勢，再基于優化后的樣本點運用最小二乘擬合進行溫度預測，并基于某型機車車輛履歷數據驗證了方法的有效性，結果表明基于PIPs樣本優化的曲線擬合預測方法能夠滿足機車車輛軸承在途預測準確性與實時性要求，對保障車輛安全運行具有一定意義。

[1]Zhou W，Habetler T G，Harley R G. Bearing condition monitoring methods for electric machines: A general review[C]//Diagnostics for Electric Machines，Power Electronics and Drives，，2007. SDEMPED 2007. IEEE International Symposium on. IEEE，2007：3-6.

[2]王躍飛，孫啟國，牛鵬. 基于Fluent的軸承腔溫度場仿真分析[J]. 機械，2014，41（3）：24-27.

[3]朱亮亮，林素敏，呂秋碩，等. 滾動軸承壽命計算方法的優化[J]. 機械，2015，42（2）：20-24.

[4]Fengqin Han，ZhonghuaGui，Kubota Takashi.Singular Spectrum Analysis-based prediction of bearing temperature trend and its application[J]. Journal of South China University of Technology（Natural Science Edition），2005，33（9）：51-54.

[5]曹寅冬. 基于新陳代謝GM（1，1）模型的客車軸溫預測算法[J].鐵道機車車輛，2011，31（1）：49-51.

[6]莫麗，王軍，王俊，王祿友. 基于GA-BP算法的旋轉控制頭軸承溫度預測[J]. 西南石油大學學報（自然科學版），2016，38（1）：164-169.

[7]王小岑，胡友名，吳波，謝鋒云，金超. 廣義隱馬爾科夫模型在軸承溫升預測中的應用[J]. 自動控制與檢測，2013（6）：54-57.

[8]Chung F L，Fu T C，Luk R，et al. Flexible time series pattern matching based on perceptually important points[C]. Proceedings of the international joint conference artificial intelligence workshop Seattle：August 2001：1–7.

A Real-Time Temperature Prediction Method Based on PIPs Sample Optimization for Train Bearings

YANG Zeyun

( CRRC QINGDAO SIFANG CO., LTD., Qingdao 266111, China )

In this paper, a bearing temperature prediction model based on the least square curve fitting is established, and the sample is optimized by using the perceptually important points to improve the prediction accuracy. First, the modeling sample points were selected from historical temperature data which can represent the important points of the temperature change trend based on the PIPs, then least squares curve fitting was used to establish a real-time temperature prediction model of train bearing temperature real-time prediction. According to a train bearing temperature data, use this model to predict temperature in the next five minutes. Compared with the actual measurement results, and it shows that the proposed temperature prediction model is valid: the total average error of the prediction model based on the least squares curve fitting is 3.47%, the total maximum relative error is 20.27%. After the improvement of PIPs, the total average prediction error is 2.67%, reduces 23.05% compared with before. The total maximum relative error is 16.67%, reduces 17.76% compared with before.

bearing temperature；time series；curve fitting；PIPs

TK730.3+22；TF068.21

A

1006－0316 (2018) 04－0001－06

10.3969/j.issn.1006-0316.2018.04.001

2017－11－20

國家高新技術研究發展計劃（863）計劃（2015AA043701）

楊則云（1980－），天津人，碩士，高級工程師，主要研究方向為機車車輛安全技術及管理。