借助圖論方法，指導數學建模

唐紀芳

[摘 要] 圖論方法是數學建模的重要方法，通過利用圖式，很多數學難題都能得以快速巧妙地解決。根據多年的教學實踐經驗，淺談了幾點借助圖論方法，指導學生數學建模的策略，旨在提高學生解決問題的能力，升華其數學素養。

[關 鍵 詞] 高職；數學建模；圖論

[中圖分類號] G712 [文獻標志碼] A [文章編號] 2096-0603（2018）08-0170-01

圖論是離散數學的一個重要分支，工程技術、自然科學、經濟管理等領域的諸多問題通過借用圖論方法建立數學模型，都能得以迎刃而解。下面筆者針對圖論的幾種重要算法及其應用展開了簡單的論述。

一、最短軌道問題，變換標號

最短軌道問題指的是在給出的一個網絡中，找出任意兩點之間的最短路線及其長度。運用圖論方法求解最短路問題時，首先需要從路線的起點開始，逐步尋找到達各點的最短路線，并且需要在每一步都對頂點記錄一個數，即做出該點的標號，隨后不斷變換標號，把一個不是最短距離標號的頂點變成是最短距離標號的頂點，最后得到最短的一條線路。應用該算法可以高效地解決交通路網的布置、景觀路線的安排、運輸路線的設計等實際問題。教師在進行教學時，可以引導學生將實際問題轉化為圖論中的最短軌道問題，抽象出數學模型。

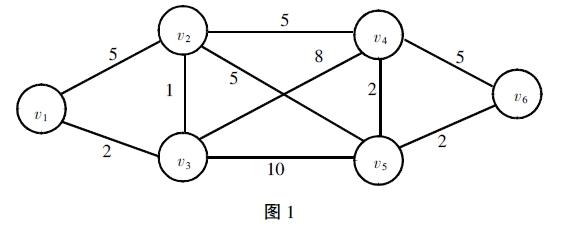
比如，筆者在對項目管理專業的高職學生進行教學時，設計了如下的問題讓學生進行作答：某建設單位A有一批鋼筋需要從城市v1運送到施工單位所在城市v6，已知六座城市v1、v2、v3、v4、v5、v6之間的路網形式如下圖所示，請問選擇哪一條運輸路線才能使成本最低呢？學生在解決這一問題時，建立了數學模型：W（P（v1，v6））=min{W（P），P取自所有v1到v6的軌道集合}，然后通過數次的迭代與標號變換，找到了最短路線：v1→v3→v2→v4→v5→v6，且最短距離為12。

二、探究Euler回路，節點配對

隨著科學技術的發展，電路結構變得越來越復雜，圖論方法在電路結構設計與計算中扮演著十分重要的角色。Euler回路是由數學家歐拉在解決“七橋問題”時創設的，對于電氣等專業的高職學生，通過應用Euler回路對復雜電路進行分析，對支路的聯結點進行配對，有助于得到最簡回路電流方程組，簡化電路的求解。

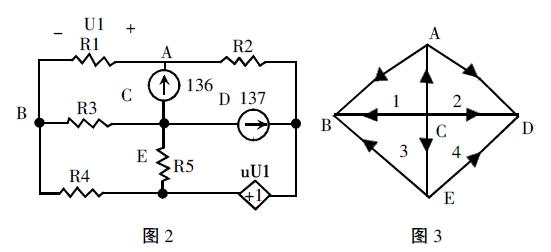
比如，筆者在引導相關專業的學生學習Euler回路時，帶大家探究了如下的電路問題：如下圖2所示，電路中有A、B、C、D、E五個節點，8條支路，13個回路……求解該電路。在探究這一問題時，筆者引導學生將歐拉回路的思想滲透到電路的分析與計算中來，選擇網孔作為一組獨立回路，4個網孔分別如下圖3所示，最后得到了7個電路方程，成功求解了該電路問題。

三、求最小生成樹，有效避圈

高職數學內容一般比較抽象，學生在解決一些涉及離散型變量的數學問題時，常常會覺得比較吃力、困難。圖論方法具有直觀形象的優點，比如說最小生成樹原理，通過用點與邊組成圖形表示現實世界中的各種關系，能夠使關系變得簡單明了，易于解決。克羅斯克爾算法也叫做“避圈法”，利用該方法能夠有效建構選線問題等題型的數學模型。因此在教學時，教師可以引導學生善于從題目中抽象出最小生成樹模型，提高他們解決專業相關問題的能力。

圖論在實際的生產生活中有著非常廣泛的應用，其內容與高職專業密切相關，教師應注重結合專業合理組合圖論的教學內容，使高職數學的教學更加專業化、高效化。

參考文獻：

[1]喬友付.數學建模在《圖論》教學中的作用[J].教育教學論壇，2013（37）：65-66.

[2]卜月華，王維凡，呂新忠.圖論及其應用[M].東南大學出版社，2015.