一款黃金結構性理財產品定價分析

程駿

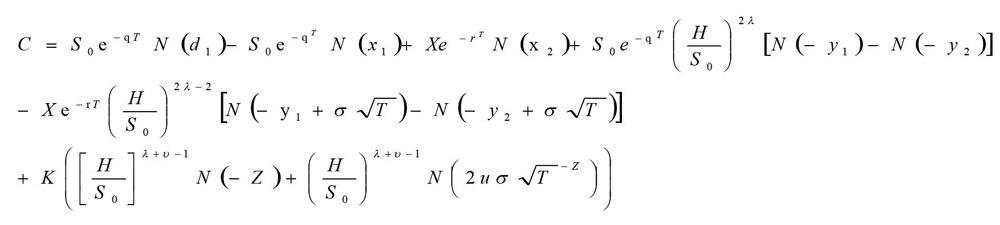
隨著社會經濟的發展，居民對財富管理的關注度也隨之增加。結構化理財產品因為其較高的預期收益率，開始越來越受到人們的喜愛。但是結構性理財產品相對來說比較復雜，掛鉤標的物種類繁多，收益率確定方式繁瑣。對于投資者雨言，無法對其預期收益作出合理的判斷。尤其是黃金掛鉤型，這種類型掛鉤的標的物價格容易產生波動。因此，本文選取黃金結構性理財產品作為研究對象。

定價 預期收益率

黃金結構性理財產品

黃金結構性理財產品定義概述

結構性理財產品是一種創新型理財工具。利用金融工程技術，將固定收益類產品與金融衍生品相結合，創造出來的新型金融產品。結構性理財產品發行者利用金融工程技術，針對不同投資者的風險偏好和承受能力將不同類型的固定收益證券和金融衍生合約進行組合，設計出風險高低各異、收益水平各異的結構性理財產品。因此，結構性理財產品的收益和風險取決于固定收益證券和衍生合約的市場表現。由于金融衍生產品市場的不確定性較大，所以相對于其他理財產品而言，結構性理財產品是高風險高收益并存的產品。不過，相較單純的金融衍生品而言，結構性理財產品的風險還是較小的。因為，由于固定收益部分的存在，風險也就得到了控制。所以，也可以簡單的描述為，結構性理財產品的風險大小取決于兩個方面：一是固定收益部分是否保本；二是鑲嵌的衍生品部分所占價值比重的大小。黃金結構性理財產品實際上是收益率與黃金相掛鉤的類型，根據不同的規則，收益率根據黃金的價格變化而變化。從產品設計角度出發，黃金結構性理財產品實際上的固定收益的證券和特殊期權的組合。結構性產品首次在我國出現的時間較晚，黃金結構性理財產品大約是在2004年之后才首次出現。

實證分析

（1）產品介紹

（2）選取原因

選取交通銀行推出的黃金掛鉤型結構性理財產品，有如此幾點原因：1.產品收益率的確定方式，是典型的復合型。同時，掛鉤方式簡單，便于計算。2.較短的存續時間，使得把利率視作靜態不變的進行計算，產生的誤差可以忽略。3.相關定價數據容易取得。

（3）基于二叉樹模型的定價

本文采用6步二叉樹方法對該產品進行定價，查得黃金歷史波動率為16.18%，無風險利率為3.5905%。所以t=l/72、F 3.5905、波動率為16.18%。根據產品條款，查得2017年8月24日當天的卜海黃金交易所交易的黃金1712當天的收盤價為279.25。將上述數據帶入軟件，估算出2017年8月的黃金期貨價格的二叉樹圖。

如二叉樹圖所示，時間為0時，黃金的價格為279.25。當時間經過t之后，出現了兩種情況。價格有概率P上漲到279.18或者概率1-P下降到268.72。以此類推，6步二叉樹法，經過6段t，得到上圖相應數據。

由于結構性理財產品比較復雜。首先要確定障礙區間為[279.25，283，44]。所以要將節點分為三個分布考慮，分別是小于區間的概率Y，區間內的概率Z和大于區間的（ 1-Y-Z）。將算出來的Y、Z帶入公式最后解出預期收益率為4.713%。

（4）基于BS模型的定價

從表4.3可知，該產品的最低收益率為2%。因此，根據結構性理財產品的定義，可以把該產品拆分為兩部分，固定收益為2%的債券和一個障礙期權。

設到期時的收益率為沒C為這個障礙看漲期權的價值，則有

根據產品信息，以2017年8月24日為標準，當天的上海黃金交易市場1712的收盤價為S0=279.25，期初價格就用279.25。無風險利率F3.5905%，在障礙區間內可以獲得的收益R-0.224乘于期初價格，查得黃金歷史波動率為16.18%

（5）基于蒙特卡洛模擬定價

選取2009年12月7日到2016年7月22日的黃金期貨為樣本，樣本量足夠多，具有統計顯著性。然后對數據做以下處理。因為選取的是同一時問段的黃金期貨價格作為樣本，對黃金期貨價格對數收益率做36階之后回歸，經檢驗，黃金價格對數收益率存在ARCH效應。用GARCH（1，1）模型，得到：最終解得，6 =0.002271 將S=273.9， 0.002271帶入，進行蒙特卡洛模擬。進行1000次模擬，最終

得到，該黃金期貨在觀察日價格小于低行權價的概率為0.24，大于高行權價的概率為0.57，落在障礙區間內的概率為0.19.所以解出結果4.672%

結論

本文具體的商品掛鉤型結構性理財產品拆分為固定收益和內含期權兩部分。固定收益部分的理論價值計算，采用現金流折現的方法。內含期權部分的理論價值計算，綜合考慮靜態波動率和動態波動率。在考慮靜態波動率時，將歷史波動率作為待選參數，運用二叉樹模型和BS模型來完成產品定價。在考慮動態波動率時，運用ARCH模型，來描述商品掛鉤型結構性理財產品掛鉤標的的未來波動。再用蒙特卡洛模擬，模擬未來不同收益率出現的概率，來確定理論預期收益率，以此完成產品定價。

從實證的結果來看：1.在運用BS模型定價得到產品的實際價值，比產品的售價要低，全部屬于溢價發行。從作為發行者的商業銀行的角度考慮，無論是產品的設計和發行成本，還是后期的管理成本，加上銀行商業銀行要獲取的盈利，適當的溢價發行都在可接受的范圍。不過，在本文的實證過程當中，交易費、管理費并沒有考慮。如果加上對上述費用的考量，產品的實際價值比文中利用BS定價模型得到的還要低。所以，從投資者角度考慮，上述產品，尤其是非保本型的理財產品，是否值得投資，還要看投資者個人的風險接受程度。2.文中利用二叉樹模型和蒙特卡洛模擬定價，得到的產品預期收益率，都比產品的最低收益率要高。但是這并不意味著，投資者就可以獲得如此的收益率。就2016年的數據來看，絕大多數結構性理財產品的到期收益率，都要遠遠小于預期收益率，其中黃金掛鉤型結構性理財產品尤為明顯。因此，投資者在選擇結構性理財產品之前，一定要對標的物的波動情況有一定的了解和預測，而非單單被預期收益率所吸引。3.蒙特卡洛模擬所得的預期收益率都比二叉樹模型所得的預期收益率要低。產生這種情況的原因，很可能是因為，在模擬過程中，標的價格路徑中會出現一些極端值。這些極端值，會影響最終的定價結果。特別是存續期較短的產品，因為在較短的時間內，很難出現這種極端情況。所以，為了避免這種極端值對整個結果的影響，可以盡可能多的增加模擬次數。

[1]陳博.結構型銀行理財產品定價與設計探討[D].碩士學位論文，復旦大學，2008.

[2]張雪瑩.銀行結構化產品定價研究[M]，中國金融出版社，2010.

[3]崔海蓉，何建敏，胡小平.避通脹風險的結構性理財產品設計與定價[J].管理科學，2012，02：105-111.

[4]馮葉.淺析銀行結構性理財產品[J]新經濟，2014，Z2： 54-56.