單位分數一變二

在學習了分數加法后，我們能很快算出下面這道題的結果：

上面這道算式出現的三個分數，分子都是1。分子是1的分數，叫作單位分數。現在我們把上面的式子倒過來寫，成為：

這樣，就變成了用一個單位分數表示另外兩個不同的單位分數的和。是不是每個單位分數都能表示成另外兩個不同單位分數的和呢？

下面我們看這樣一道題：在下面的（ ）里填上不同的數，使等式成立。

利用分數的基本性質，可以做下面的變形：

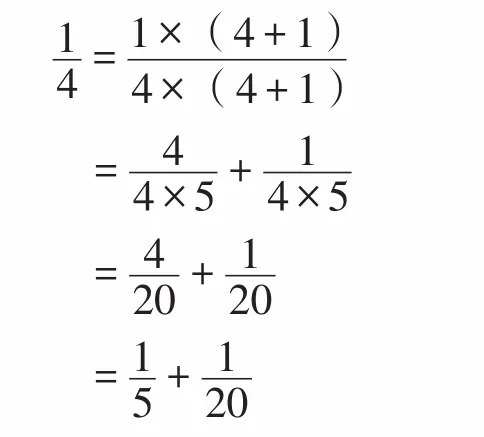
所以，得到：

這種方法適用于任何單位分數。例如，取分母是8，可寫出：取分母是100，可很快寫出：

你看，很巧妙吧！為什么不用計算，就能立刻寫出等式？

這里有一個很簡單的規律：用原有單位分數的分母（n）加上1，得到n+1，作為拆開后第一個新單位分數的分母；再拿新分母n+1和原分母n相乘，得到n（n+1），作為拆開后另一個新單位分數的分母。這樣，可以得到一個公式：

○小試牛刀

題目：在等式的括號里填入不同的數，使等式成立。