基于自適應抗差卡爾曼濾波的UWB室內定位*

劉 韜,徐愛功,隋 心

(遼寧工程技術大學測繪與地理科學學院,遼寧 阜新 123000)

近年來,隨著無線通信和無線傳感器網絡的不斷發展,無線定位技術越來越受到人們的關注,廣泛應用于災害急救、目標跟蹤、車載導航、行人導航等領域[1]。以全球衛星導航系統為基礎的室外定位技術已趨于成熟;在室內定位中,超寬帶UWB(Ultra-Wide Band)技術利用功率譜密度極低、脈沖寬度極窄的脈沖信號傳輸數據,具有時間分辨率極高、障礙穿透能力強等特點,在視距LOS(Line-Of-Sight)環境下能獲得厘米甚至毫米級的測距和定位精度[2-3],適用于室內環境下的高精度定位。

由于墻體和障礙物的存在,UWB信號通過折射和反射在移動站和基準站之間進行傳播,從而形成非視距NLOS(Non-Line-Of-Sight)誤差,極大降低其測距精度,使定位結果產生較大的誤差[4-8]。文獻[4-5]對大量LOS和NLOS環境下的UWB信號波形特征進行分析,利用支持向量機進行NLOS狀態的鑒別和誤差削弱,能有效消除NLOS誤差并提高測距精度,但該方法建立在大量的數據統計上,工作量較大;文獻[6]針對LOS/NLOS環境下的定位,利用粒子濾波和無跡卡爾曼濾波方法進行定位和測速,能有效抑制NLOS誤差的影響,但其算法復雜,實現困難;文獻[7]利用基于往返時間RTT(Round Trip Time)和基于到達角度AOA(Angle Of Arrival)的方法進行混合測距,并提出了基于網格的聚類定位算法,其不需要室內環境的先驗信息,仿真效果明顯,但AOA方法需要天線陣列,會增加硬件成本;文獻[8]利用慣性導航INS(Inertial Navigation System)輔助UWB進行定位,通過先驗閾值進行NLOS判斷,利用INS的短期高精度結果鑒別NLOS誤差并消除其影響,但該方法需要增加硬件成本,且算法也更復雜。

UWB測距不僅會受到NLOS測距誤差的影響,還會受到由實驗環境、儀器硬件和人為干擾等因素產生的測距異常值的影響,這兩個測距誤差均表現為量測信息異常,從而導致距離濾波和定位解算出現異常。針對量測信息異常的問題,有學者提出抗差估計理論抵制量測信息異常誤差的影響[9]。文獻[10]結合神經網絡和卡爾曼濾波構建自適應因子,自適應調節狀態向量和量測噪聲的協方差矩陣,從而抑制異常信息對濾波結果的影響,但神經網絡需要大量理想的樣本進行訓練;文獻[11]針對GNSS/INS組合系統,利用新息向量構建抗差因子并作用于量測噪聲的協方差矩陣,從而修正濾波增益矩陣,提高系統的精度和抗差性。

在UWB定位中,很難用一個準確的統計特征來描述系統噪聲。針對上述問題,本文提出了一種抗差自適應濾波算法并應用于UWB測距和定位。該算法首先在UWB距離模型的基礎上,利用新息向量和LOS環境下的閾值鑒別量測信息是否出現異常,進一步構建量測噪聲的抗差協方差矩陣,在濾波過程中利用改進的Sage-Husa濾波的次優無偏極大后驗估計特性對系統噪聲的協方差矩陣進行實時估計和修正,削弱并消除NLOS測距誤差和測距異常值的影響,得到更準確穩定的測距信息;然后推導并構建UWB定位的線性模型,利用卡爾曼濾波得到載體的位置和速度信息。

1 距離濾波方法

1.1 距離模型

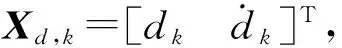
Xd,k=Fd,k-1Xd,k-1+wd,k

(1)

以RTT方法量測的距離值作為量測信息,則距離模型的量測方程為:

Zd,k=Hd,kXd,k+Vd,k

(2)

1.2 自適應抗差卡爾曼濾波

由于式(1)和式(2)組成的距離模型為線性模型,其標準卡爾曼濾波[8,14]KF(Kalman Filter)算法為:

(3)

(4)

式中:c為閾值,可通過UWB基準站和流動站之間為LOS環境下多次測量確定。采用Huber函數[9-11]方法構建量測噪聲的抗差協方差矩陣,即:

(5)

在UWB測距過程中,很難用一個準確的統計特征來描述系統噪聲,而Sage-Husa濾波能對系統噪聲統計特性進行實時估計和修正,從而進一步提高濾波的精度,且具有一定的抗干擾能力[15-17]。結合文獻[16],利用改進的Sage-Husa濾波對系統噪聲的協方差矩陣進行實時估計:

(6)

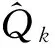
在計算預測狀態協方差矩陣時,利用式(6)對系統噪聲的協方差矩陣不斷進行實時估計和修正,進而減小狀態估計誤差,并結合式(5),實現UWB距離模型的自適應抗差卡爾曼濾波ARKF(Adaptive Robust Kalman Filter)過程,在抑制量測信息異常誤差的同時進一步提高濾波解算的精度,得到更準確可靠的UWB測距信息。

針對自適應抗差卡爾曼的距離濾波方法,利用一組靜止的UWB測距信息進行分析驗證。靜止數據由Time Domain的PulsON400通信與測距模塊采集,采樣頻率為2 Hz,共采集2 000 s,數據采集過程中有人員在UWB基準站和流動站之間隨機走動,同時對UWB天線進行隨機遮擋。原始的RTT測距信息如圖1所示。

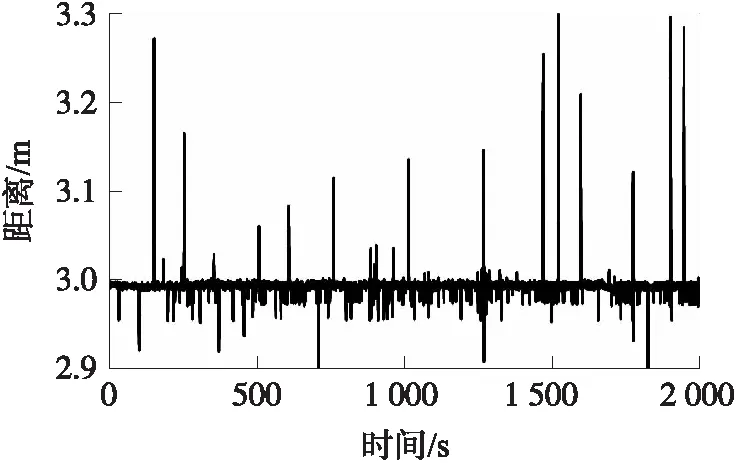
圖1 RTT測距信息

由圖1可以看出測距中存在大量的NLOS誤差和測距異常值。在對標準時間偏差誤差進行改正之后,利用卡爾曼濾波、Sage-Husa自適應濾波和文中的自適應抗差卡爾曼濾波方法進行濾波計算,利用全站儀觀測計算的距離作為參考真值進行比較分析。

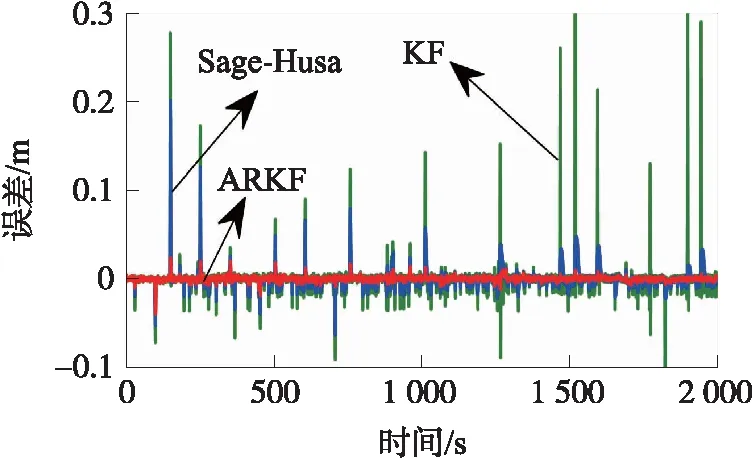
圖2 3種濾波方法的測距誤差

圖2給出了3種方法的測距誤差,表1給出3種方法的誤差統計信息。結合圖2和表1,相較于卡爾曼濾波和Sage-Husa自適應濾波,自適應抗差卡爾曼濾波的最大誤差能從3 dm降低至4 cm,其測距精度更高、穩定性更強。可以看出:自適應抗差卡爾曼濾波方法利用抗差估計理論能有效抑制UWB測距中的NLOS測距誤差和測距異常值,同時結合Sage-Husa自適應濾波對系統噪聲進行實時的估計和修正,進而提高UWB測距的精度和穩定性。

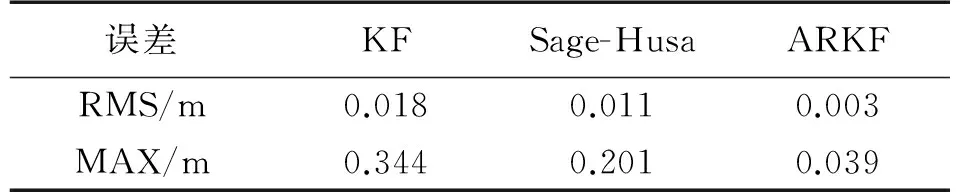
表1 3種濾波方法的測距誤差統計

2 UWB定位方法

在UWB平面定位中,利用3個及3個以上置于固定位置的UWB基準站和1個流動站進行定位[8,18]。以流動站的位置和速度信息作為狀態參數Xp,k=[xkykvx,kvy,k]T,則UWB定位的狀態方程為:

Xp,k=Fp,k-1Xp,k-1+wp,k

(7)

式中:xk和yk分別為第k時刻UWB流動站在x和y方向的位置,vx,k和vy,k分別為第k時刻UWB流動站在x和y方向的速度,Fp,k為系統狀態轉移矩陣,wp,k為系統噪聲,wp,k為零均值的高斯白噪聲,其對應的協方差矩陣為Qp,k,且有:

(8)

(9)

式中:ΔTk為UWB數據采樣間隔,q為系統噪聲的功率譜密度。

通過距離濾波方法對原始RTT測距信息進行處理,削弱并消除測距中的NLOS測距誤差和測距異常值的影響,得到更準確可靠的測距信息。那么,第k時刻第i個UWB基準站和流動站之間的距離di,k可表示為:

(10)

對式(10)進行變形后,可以得到:

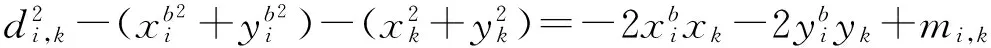
(11)

Zp,k=Hp,kXp,k+Vp,k

(12)

式中:Hp,k為量測矩陣,Vp,k為k時刻的量測噪聲,Vp,k為零均值的高斯白噪聲,其對應的協方差矩陣為Rp,k,且有:

(13)

(14)

在UWB定位的狀態方程和量測方程中,其系統噪聲和量測噪聲互不相關。由于式(7)和式(11)組成的UWB定位模型為線性模型,在假設系統噪聲和量測噪聲為高斯白噪聲的前提下,利用式(3)的卡爾曼濾波方法能最優估計UWB流動站的位置和速度信息。

圖3 室內實驗場景

3 實驗與分析

實驗數據由Time Domain的PulsON400通信與測距模塊采集,其帶寬為3.1 GHz～5.3 GHz,數據采樣頻率為2 Hz,利用RTT方式測得UWB流動站與基準站間的距離,在LOS環境下測距精度為厘米級。為了驗證本文算法的有效性,分別利用卡爾曼濾波(KF)、Sage-Husa自適應濾波(Sage-Husa)和文中的自適應抗差卡爾曼濾波(ARKF)進行距離濾波,然后再進行定位解算。在如圖3所示的室內環境下分別進行靜態定位和動態定位實驗。

靜態實驗中,將3個UWB基準站置于固定位置,利用全站儀確定其坐標,并假設其沒有誤差,UWB流動站靜止不動,以全站儀觀測的UWB流動站坐標作為參考真值,實驗時長約為6 min,實驗過程中有多人隨機在實驗場中走動。圖4給出3個UWB原始的RTT測距信息,可以看出其中存在部分的NLOS測距誤差和測距異常值,圖5和圖6給出了3種濾波方法在x和y方向上的定位誤差,表2給出了3種濾波方法的誤差統計。

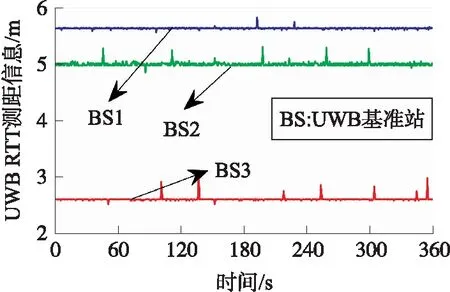
圖4 靜態實驗中的UWB測距信息

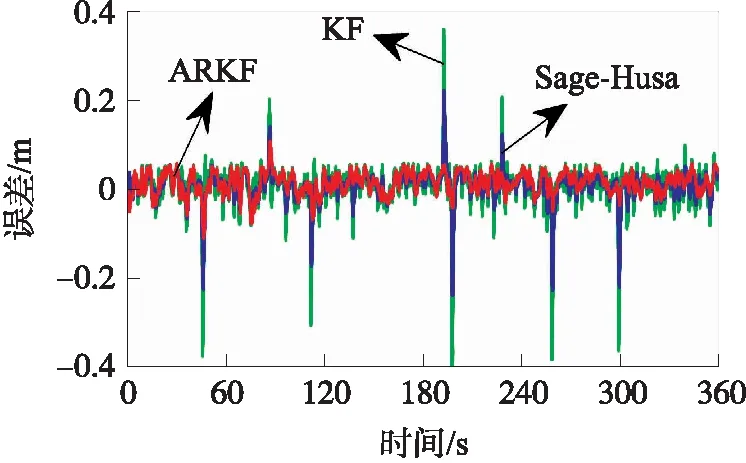
圖5 3種濾波方法在x方向的位置誤差

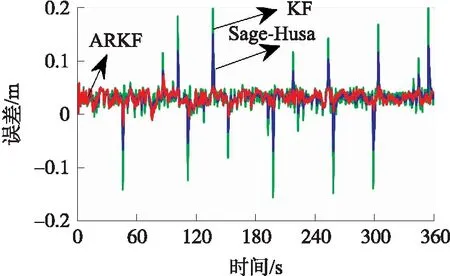
圖6 3種濾波方法在y方向的位置誤差

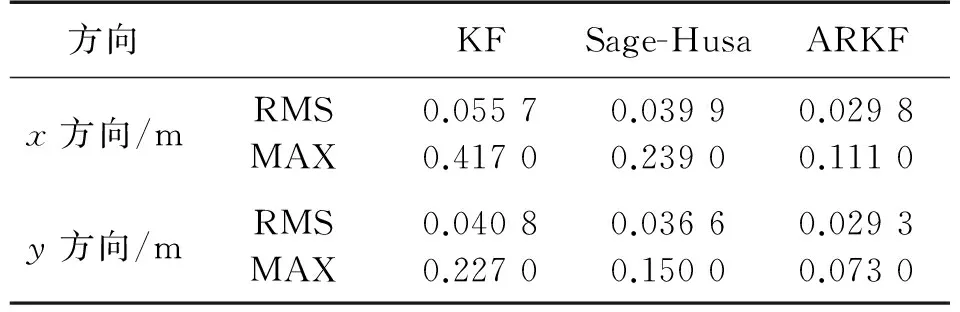
表2 靜態實驗中3種濾波方法的誤差統計

在動態實驗中,將3個UWB基準站置于固定位置,利用全站儀確定其坐標,并假設其沒有誤差,將UWB流動站置于實驗小車上,人員推著實驗小車移動,利用全站儀確定的UWB流動站的位置作為參考軌跡,實驗時長500 s。圖7給出了3個UWB原始的RTT測距信息,其中藍色、紅色和綠色線分別為測得的第1個、第2個和第3個UWB基準站與流動站之間的距離,由于遮擋導致測距中存在NLOS測距誤差和測距異常值。

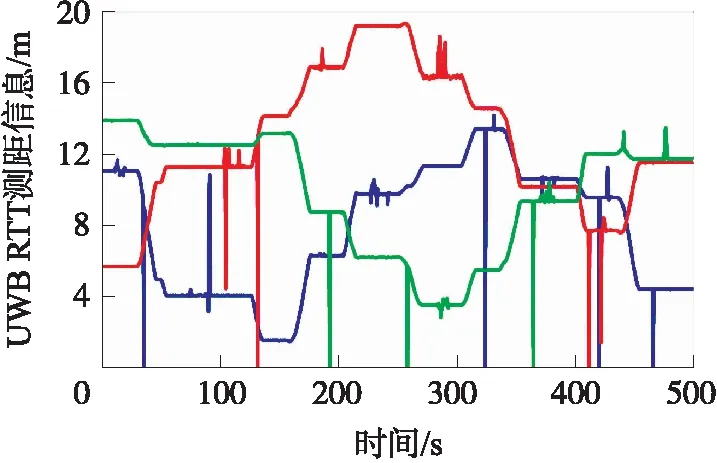
圖7 動態實驗中UWB測距信息

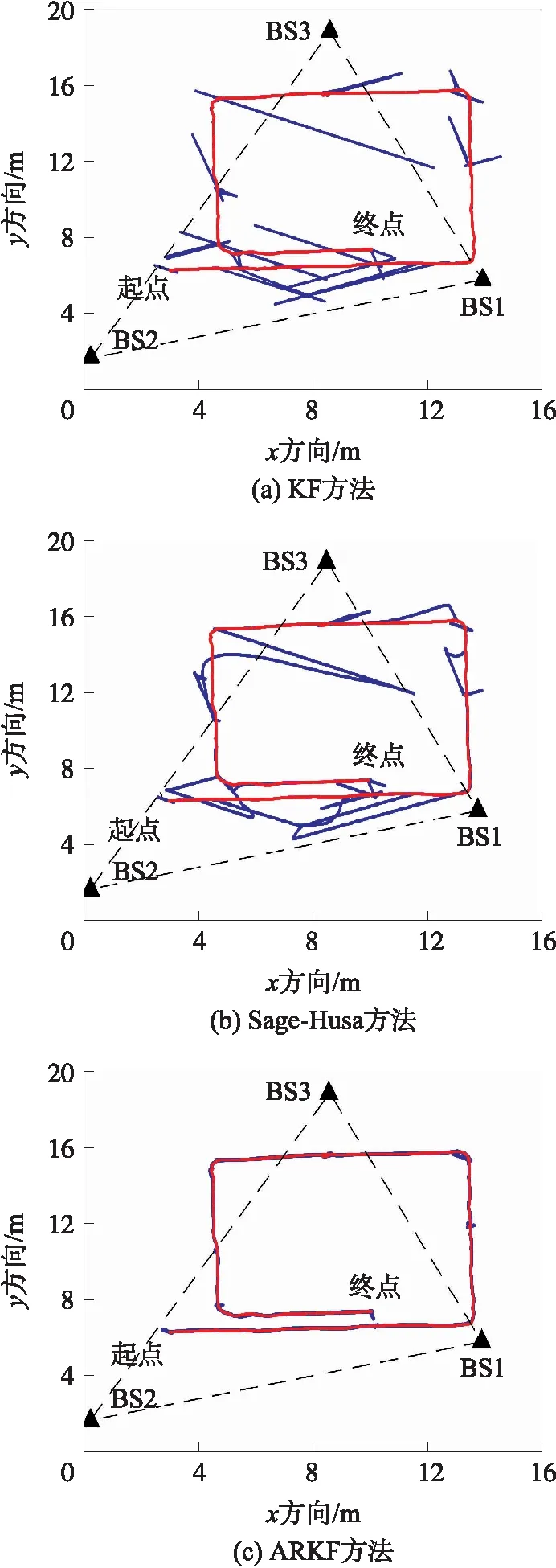
圖8 動態實驗中3種濾波方法解算的動態軌跡

利用3種方法進行距濾波,然后進行距離解算,圖8給出了3種方法的平面軌跡,其中紅色實線為參考軌跡。圖9和圖10分別給出了3種濾波方法在x和y方向上的定位誤差,其中綠色、藍色和紅色線分別為KF、Sage-Husa和ARKF方法的誤差,表3給出了3種濾波方法的誤差統計。

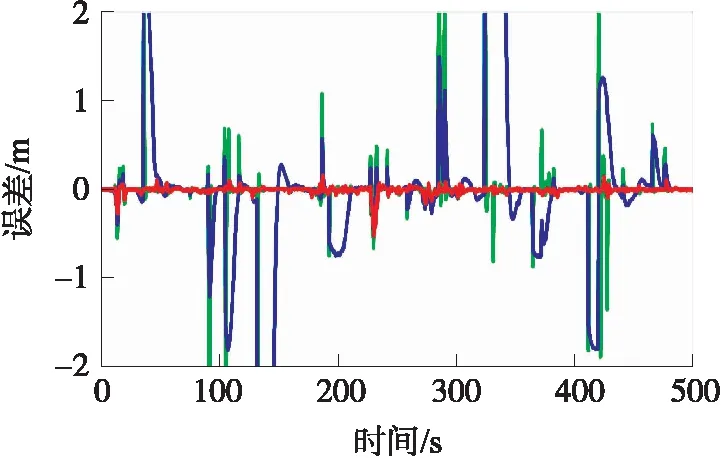
圖9 動態實驗中3種濾波方法在x方向的位置誤差

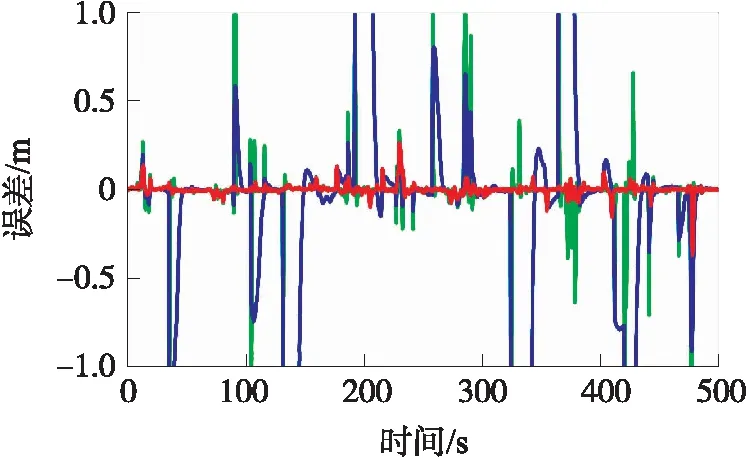
圖10 動態實驗中3種濾波方法在y方向的位置誤差

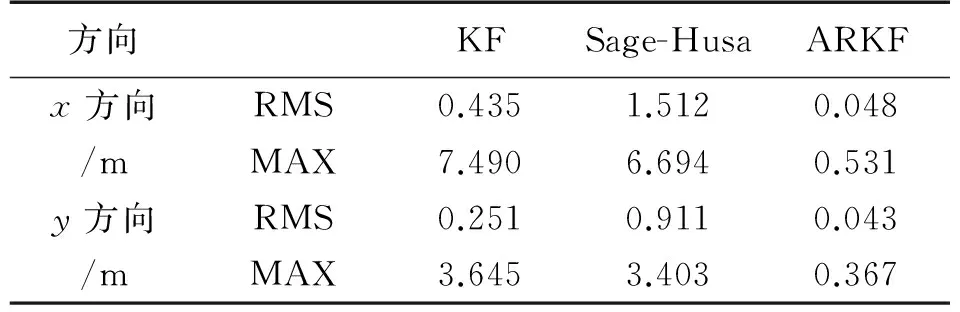
方向KFSage-HusaARKFx方向/mRMSMAX0.4357.4901.5126.6940.0480.531y方向/mRMSMAX0.2513.6450.9113.4030.0430.367

分析以上實驗結果,可以得出:

①當UWB的RTT測距中出現NLOS測距誤差和測距異常值時,利用卡爾曼濾波方法進行距離濾波時,其完全不具有抗差性,濾波結果誤差較大,再進行定位解算時,UWB定位的精度和穩定性難以得到保障;

②利用Sage-Husa自適應濾波進行距離濾波時,靜態情況下具有一定的抗差性,能提高測距的精度和穩定性,從而提高靜態定位的精度和可靠性;然而在動態環境下,由于實驗小車運動的不規律性,同時受到實驗環境等因素的影響,很難同時精確地估計系統噪聲和量測噪聲,UWB定位結果的精度和穩定性難以提高,一旦濾波發散,錯誤的濾波值會污染測距良好情況下的定位結果,反而導致定位精度降低;

③利用文中提出的自適應抗差卡爾曼濾波進行距離濾波時,其依據抗差估計理論對NLOS測距誤差和測距異常值進行抗差處理,能提高UWB測距的精度和穩定性,同時利用Sage-Husa自適應濾波對系統噪聲進行估計和修正,能綜合二者的優勢,進一步提高距離濾波的精度和可靠性,進而得到精度更高、穩定性更好的UWB定位結果。

4 結論

在UWB室內定位中,測距過程中受到NLOS測距誤差和測距異常值的影響,UWB定位精度會大幅下降,從而降低其穩定性和可靠性。本文將抗差估計理論和Sage-Husa自適應濾波用于UWB測距中的距離估計,并提出了針對UWB距離濾波的自適應抗差濾波方法,在此基礎上推導了線性化的UWB定位模型,通過卡爾曼濾波計算載體的位置和速度信息。在室內環境下設計了UWB測距、靜態定位和動態定位實驗,將文中提出的方法與卡爾曼濾波和Sage-Husa自適應濾波進行了對比和精度分析。實驗結果表明,文中提出的自適應抗差卡爾曼濾波方法能有效地消除并改正UWB測距中的NLOS誤差和異常測距值,提高UWB測距的精度和穩定性,在此基礎上利用卡爾曼濾波進行定位,能提升UWB定位的精度和可靠性。

參考文獻:

[1] Liu H,Darabi H,Banerjee P,et al. Survey of Wireless Indoor Positioning Techniques and Systems[J]. IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2007,37(6):1067-1080.

[2] de Angelis G,Moschitta A,Carbone P. Positioning Techniques in Indoor Environments Based on Stochastic Modeling of UWB Round-Trip-Time Measurements[J]. IEEE Transactions on Intelligent Transportation Systems,2016,17(8):2272-2281.

[3] Alarifi A,Al-Salman A M,Alsaleh M,et al. Ultra Wideband Indoor Positioning Technologies Analysis and Recent Advances[J]. Sensors,2016,16(5):1-36.

[4] Stefano M,Wesley M,Henk W,et al. NLOS Identification and Mitigation for Localization Based on UWB Experimental Data[J]. IEEE Journal on Selected Areas in Communications,2010,28(7):1026-1035.

[5] Wymeersch H,Maranò S,Gifford W M,et al. A Machine Learning Approach to Ranging Error Mitigation for UWB Localization[J]. IEEE Transactions on Communications,2012,60(6):1719-1728.

[6] Huerta J M,Vidal J,Giremus A,et al. Joint Particle Filter and UKF Position Tracking in Severe Non-Line of Sight Situations[J]. IEEE Journal of Selected Topics in Signal Processing,2009,3(5):874-888.

[7] 毛科技,鄔錦彬,金洪波,等. 面向非視距環境的室內定位算法[J]. 電子學報,2016,44(5):1174-1179.

[8] 劉韜,徐愛功,隋心. 超寬帶與慣性導航組合的室內導航定位[J]. 測繪科學,2016,41(12):162-166.

[9] Yany Y X,He H,Xu G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy,2001,75(2):109-116.

[10] 高為廣,陳谷倉. 結合自適應濾波和神經網絡的GNSS/INS抗差組合導航算法[J]. 武漢大學學報(信息科學版),2014,39(11):1323-1328.

[11] 苗岳旺,周巍,田亮,等. 基于新息x2檢測的擴展抗差卡爾曼濾波及其應用[J]. 武漢大學學報(信息科學版),2016,41(2):269-273.

[12] 徐愛功,劉韜,隋心,等. UWB/INS緊組合的室內定位定姿方法[J]. 導航定位學報,2017,5(2):14-19.

[13] de Angelis A,Nilsson J,Skog I,et al. Indoor Positioning by Ultrawide Band Radio Aided Inertial Navigation[J]. Metrology and Measurement Systems,2010,17(3):447-460.

[14] 王瑞榮,鄭書萬,陳浩龍,等. 一種基于Taylor和Kalman的室內協同定位方法[J]. 傳感技術學報,2014,27(11):1557-1561.

[15] Sage A P,Husa G W. Adaptive Filtering with Unknown Prior Statistics[C]//Proceedings of Joint Automatic Control Conference,1969:760-769.

[16] 魏偉,秦永元,張曉東,等. 對Sage-Husa算法的改進[J]. 中國慣性技術學報,2012,20(6):678-686.

[17] Peng S,Chen C,Shi H,et al. State of Charge Estimation of Battery Energy Storage Systems Based on Adaptive Unscented Kalman Filter with a Noise Statistics Estimator[J]. IEEE Access,2017,5:13202-13212.

[18] Kok M,Hol J D,Sch?n T B. Indoor Positioning Using Ultrawideband and Inertial Measurements[J]. IEEE Transactions on Vehicular Technology,2015,64(4):1293-1303.