基于時間序列數據的無線傳感器網絡的異常檢測方法*
彭能松,張維緯*,張育釗,黃 焯,鄭力新
(1.華僑大學工學院,福建 泉州 362000;2.工業智能化技術與系統福建省高校工程研究中心,福建 泉州 362000)
無線傳感器網絡WSN(Wireless Sensor Networks)作為溝通主觀感知世界和客觀物理世界的橋梁,是一種全新的信息獲取和處理技術,是物聯網的重要支撐技術之一,已經得到了迅速的發展和廣泛的應用[1],包括國防、軍事、醫療保健、環境監測、制造業和其他許多領域[2-3]。
隨著無線傳感器網絡規模的增加,傳感器網絡的異常檢測越發的關鍵。尤其是對于一些緊急事件,例如化學物質泄漏、火災等,往往需要及時預警并采取緊急處理措施。但是,惡劣的部署環境和傳感器本身的不可靠性導致傳感器產生錯誤的讀數,從而影響傳感器網絡的異常檢測。
現有的空間離群檢測算法通常分為三步[4-5]:首先,通過最小鄰數來確定基于空間屬性的鄰域關系。其次,使用空間屬性來計算離群的程度,捕獲對象與其空間鄰域之間的差異。最后,將具有最大空間離群度的n個對象輸出為異常點。在進行空間離群檢測時需要與鄰居節點交換信息,額外的通信會加快傳感器節點能量的消耗。外部的因素或傳感器節點自身的問題(如能量耗盡等),導致無線傳感器網絡錯誤節點增加,利用WSN的空間屬性將降低事件的檢測率。
WSN的時間屬性記錄著周圍環境隨時間的變化規律,當事件發生時,例如火災發生時溫度會在短時間內急劇上升。也就是說,事件發生后會持續一段時間,并且事件的特征隨著時間具有某些變化規律。利用WSN的時間屬性進行異常檢測具有很高的研究價值。對無線傳感器網絡中的異常數據進行檢測通常要考慮兩個問題[6]:①錯誤傳感器會影響整個網絡對事件的檢測;②傳感器能量有限,應盡量減少網絡中消息通信,降低傳感器能源的消耗。
基于此,本文從傳感器網絡的時間屬性入手,采用分布式檢測方法對傳感器網絡進行異常檢測。實驗結果和分析表明了本文方法減少了錯誤傳感器對事件檢測的影響,提高了事件的檢測率并降低了傳感器節點能量的消耗。
本文第1節介紹已有的相關工作及研究成果;第2節將介紹傳感器網絡異常檢測的方法及相關定義,并給出本文使用的符號定義;第3節介紹基于時間序列的無線傳感器網絡異常檢測方法;第4節是實驗結果及分析;最后是本文的小結。
1 相關工作
Krishnamachari B等[7]最早提出一種分布式的局部算法,通過空間(鄰居節點)交換感知信息(0表示正常數據,1為非正常數據),統計鄰居檢測到事件的概率,結合節點故障概率,最后利用Bayesian分析的方法,決定是否發生了錯誤或事件。李桂丹等[8]提出一種分布式的容錯事件邊界檢測算法,節點通過和鄰居節點交換一次信息,通過簡單地計算識別故障;并利用統計比較的方法判斷其是否處于事件邊界。這種方法算法復雜度低,容錯性高。但比較依賴傳感器網絡的密度,密度越大檢測率越高。魏暢[9]等提出一種基于約簡策略與自適應SVDD(Support Vector Data Description)的離群檢測方法,利用基于數據分布密度準則和數據流時間相關性自適應更新決策模型,取得了很好的檢測效果。高建良等[10]提出了基于加權中值的故障診斷策略,對鄰居節點測量數據進行進行加權處理,測量數據之間差距的方法來檢測故障節點,但文中沒有涉及事件的檢測。費歡[11]等改進k-means 算法,根據無線傳感器數據特點,采用歐氏距離為指標,根據數據到聚類中心的距離判斷數據的異常。姜旭寶等[12]提出一種基于變寬直方圖的異常數據檢測算法,將相同特性的高頻區域合并,減少不必要的數據傳輸,降低網絡開銷。曹冬磊等[13]從事件的時空相關性入手,提出了一種分布式的無線傳感器網絡事件區域檢測的容錯算法,通過檢驗事件隨機過程的統計特征和傳感器本地采樣值構成的時間序列的符合程度來實現容錯,但隨著網絡錯誤節點的增加,事件檢測率也隨之降低。趙志剛[14]將傳統的置信區間用于異常數據的檢測,在實際應用中取得很好的檢測效果。李云飛[15]提出一種中位數的置信區間討論了Ⅰ型極小值分布總體位置參數和尺度參數的區間估計問題。
受文獻[14-15]的啟發,本文將改進的置信區間用來檢測數據是否存在異常。借鑒文獻[11,16]采用距離檢測離群點的思想,結合文獻[13]的事件閾值函數,提出區間差異度的概念,作為異常來源的判斷。并針對以往成果的不足:采用空間屬性的異常檢測方法對傳感器網絡密度要求高以及當錯誤節點增加事件檢測率降低,誤報率增加。本文從時間序列數據入手提出了以時間序列為基礎的無線傳感器網絡異常檢測方法,實現采樣集中異常值的檢測,識別故障節點和事件節點。
2 WSN異常檢測基本原理
一般當傳感器在連續的一段時間內,檢測的數據偏離正常的數據,就可以認為有異常發生。而導致異常的原因有很多,特定區域發生事件稱為事件異常;由自身故障或外部引起的稱為發生故障或發生錯誤。
由于采用傳感器網絡空間屬性將加快節點能量消耗,隨著無線傳感器網絡故障節點的增加,事件檢出率降低的問題。因此本文的檢測方法采用傳感器網絡時間序列數據。改進置信區間,估計小范圍的總體樣本波動區間,用于異常值的檢測,再利用區間差異度判斷異常的來源。
2.1 時間序列數據模型
本文從WSN的時間相關性角度分析,在進行數據分析前需先建立一個時間序列數據模型。假設在監測區域隨機的部署有n個傳感器進行數據的采集。傳感器節點通過底層時間同步機制保證采集和傳輸的數據同步性。
由于傳感器節點的存儲能力有限,不能滿足時間序列數據的無限增長性,本文采用滑動窗口處理數據,節點只保存最新的k個數據。滑動窗口具體定義為:
定義1滑動窗口模型(Sliding Window Model)[17]為數據流最新的k個數據元素維護一個窗口,假設新數據元素從右邊進來,當新數據元素到達,最左邊的元素將過期,窗口向右滑動一個數據元素。
假設在某一個采樣周期內,任一傳感器采集的數據集為R(ti)={r(t1),r(t2),…,r(tn)}其中t1,t2,…,tn為采樣時刻。設節點當前的窗口數據為{r(t1),r(t2),…,r(tp)},當新數據r(tp+1)到達且為正常數據時,窗口向前滑動,同時將窗口中的數據更新為{r(t2),r(t3),…,r(tp+1)},后續的數據以此類推。
當建立滑動窗口模型之后,要對時間序列數據計算置信區間和區間差異度。
2.2 置信區間和區間差異度
2.2.1 置信區間
如何確定傳感器t時刻的讀數r(t)是否異常,傳統的閾值方法存在閾值范圍難以確定的問題,太小或太大會產生誤報或者漏報。而傳感器網絡采集的數據在不同的部署環境具有不同的特點,例如在某些溫度變化很大的環境中,即使數據變動較大,數據也是正常的;而在有些穩定的環境下,有可能小的波動就是異常。根據數據特點采用置信區間判斷異常值。
在自然條件下假設正常數據在范圍[a,b]內波動,而異常數據往往與正常數據有較大的差異,一般反映為樣本的極值,它們會對統計推斷帶來不良的影響[15],而樣本的中位數能很好的抵抗異常值的干擾,越靠近中位數的樣本其抵抗能力越強[18],因此本文采用中位數構造樞軸量。
設X1,X2,…,Xn是來自均勻分布的總體X~U(a,b)的獨立同分布樣本,設med為樣本X1,X2,…,Xn的中位數[15]。
(1)
在方差δ2未知的情況下采用樣本方差S2來計算中位數的置信區間[14]。
(2)

(3)
易驗證T為關于μ的樞軸量,對于給定的α,令
(4)
即
(5)
得到置信度為1-α的置信區間
(6)
由式(6)知該區間為總體樣本中位數的一個估計區間,將式(6)做相應的變形得到總體樣本的估計區間。
(7)
式(7)即為總體樣本區間估計,但區間估計的精度受樣本數k和置信度α的影響較大,樣本數k和置信度α的選擇將在實驗結果及分析中說明。
2.2.2 區間差異度
為了定性的描述傳感器t時刻的讀數r(t)與總體樣本{r(t1),r(t2),…,r(tp)}的關系,即r(t)與置信區間[LCL,UCL]的差異。而衡量個體差異的方法有很多,主要分為兩大類:距離度量和相似度度量,其中距離度量主要有歐幾里得距離和明可夫斯基距離等;相似度度量包含向量空間余弦相似度和皮爾森相關系數等。本文根據距離度量的思想提出區間差異度的概念,定義如下:
定義2區間差異度:對于樣本空間點rt(i),其區間差異度γ表示rt(i)與置信區間的差異程度,公式如下:
(8)
式中:rt(i)為傳感器t(i)時刻的讀數,UCL(Upper Confidence Limit)為置信區間上限,LCL(Lower Confidence Limit)為置信區間下限。γ表示t(i)時刻的讀數與置信區間的差異程度,γ越大說明傳感器讀數距離總體樣本越遠,為異常值的可能性越大。
在本文中只考慮異常值大于正常值的情況,若檢測異常值小于正常值的情況只需將式(8)換為式(9)即可。
(9)
當檢測到異常值后需要驗證異常值的來源,判斷是節點異常還是突發事件,首先對判斷條件進行分析。
(10)
(11)
式中:Rth(t)為判斷事件的閾值函數[13],En(t)是正確的傳感器在正常區域中的讀數的期望函數;Ee(t)是正確的傳感器在事件區域中讀數的期望函數。ξ是判斷是否發生事件的重要指標,如果區間差異度大于ξ,則認為發生事件。
綜上,置信區間對樣本總體參數估計及差異度采用距離衡量類間相似程度的思想為進行異常值檢測提供了理論基礎,在此基礎上,本文提出了一種利用WSN時間序列數據進行異常檢測的方法。本文的方法不僅適用于高密度的傳感器網絡,對于低密度非均勻分布的傳感器網絡同樣適用。
本文中使用的符號和術語定義如表1所示。

表1 符號定義
3 異常檢測
本節將給出一種以WSN時間序列為基礎,分為異常數據識別,異常來源驗證兩個步驟,利用置信區間識別傳感器數據集中可能存在的異常數據點,在檢測到異常數據點后,需計算γ和ξ從而區分其異常來源。下文將分別進行詳細說明。
3.1 異常數據識別
在自然環境下,傳感器的采樣值rt(i)表現為在小范圍內小幅度的波動,但出現異常時則會在短時間內出現明顯的偏差[18],且事件特征至少可以持續Tth時間[13]。
傳感器節點里保存k個正常數據,數據可在部署前保存在傳感器節點里或部署后節點保存采集的正常數據。利用k個正常值和給定的置信度α計算得到總體樣本的區間估計[LCL,UCL]。如果r(t)不滿足式(12),那么該測量值可能為異常數據。
LCL≤r(t)≤UCL
(12)
式中:UCL,LCL分別為置信區間的上下限,r(t)為t時刻采樣值,當r(t)滿足(12)時更新滑動窗口的數據元素。
此外,當傳感器節點發生故障時,可能在連續的采樣時刻內產生同樣的讀數[19],即
r(t)=r(t-1)
(13)
將式(12)和式(13)稱為判斷傳感器讀數是否異常的判斷條件。
3.2 異常來源驗證
當某個傳感器t時刻的讀數r(t)的值不在區間[LCL,UCL]內或r(t)=r(t-1)時就認為發生了異常;為確定異常來源需要計算數據與置信區間的區間差異度γ和ξ,在Tth時間內,計算m次區間差異度的值,并計算平均值μ(γ)如果μ(γ)<1可以認為是由測量誤差或置信區間預估偏差引起的。
如果μ(γ)>ξ且r(t)≠r(t-1),認為該節點檢測到事件。
如果μ(γ)<ξ或r(t)=r(t-1),認為該節點發生錯誤。當節點發生故障時,傳感器采集的前一刻數據可能丟失,為了避免數據的丟失,在傳感器節點發生故障前將數據備份到鄰居節點。當m/2次滿足條件(μ(γ)<ξ或r(t)=r(t-1))時,認為該節點即將發生故障,這時將該傳感器節點的數據向所有鄰居節點傳播。
本文的偽代碼描述如下:
Input:r(t),En(t),Ee(t),Tth,ΔT,k,α,Rth(t);
Calculating confidence intervals
if(LCL<=r(t)<=UCL andr(t)!=r(t-1)){
Update sliding window
status=Normal;
}
else{
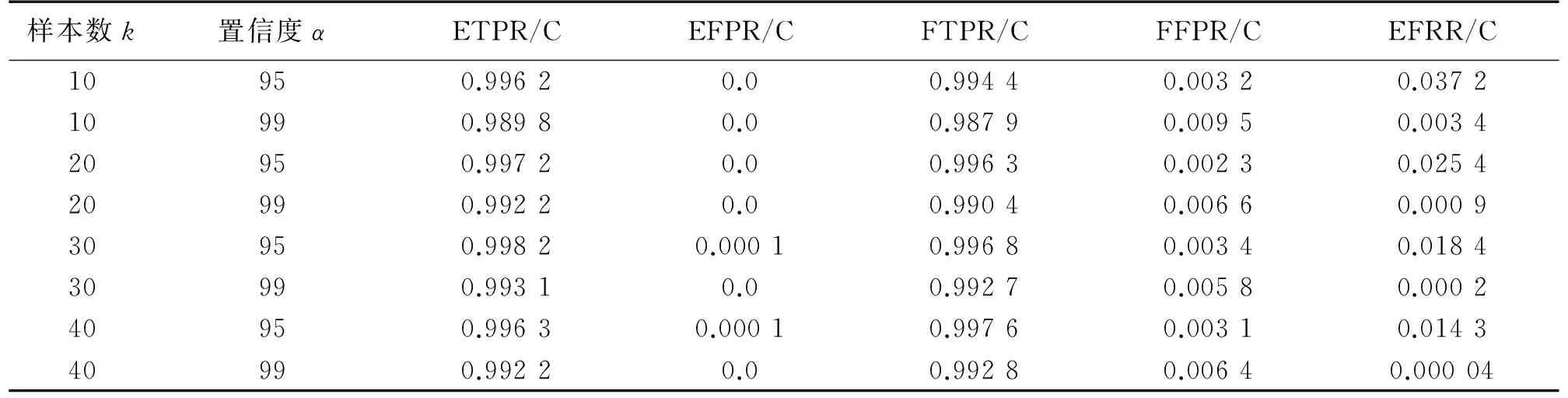
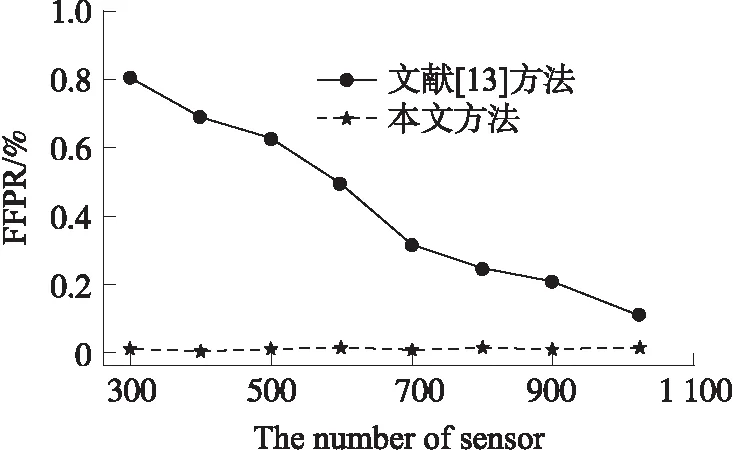
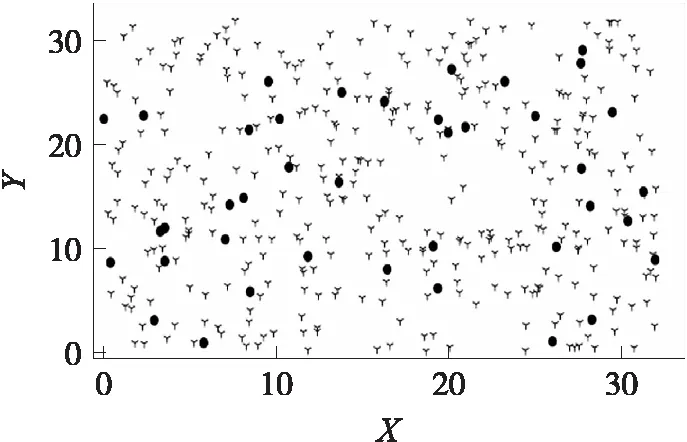
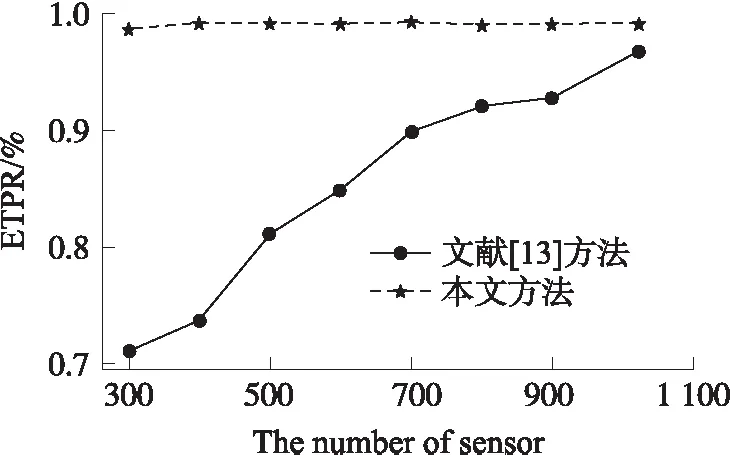
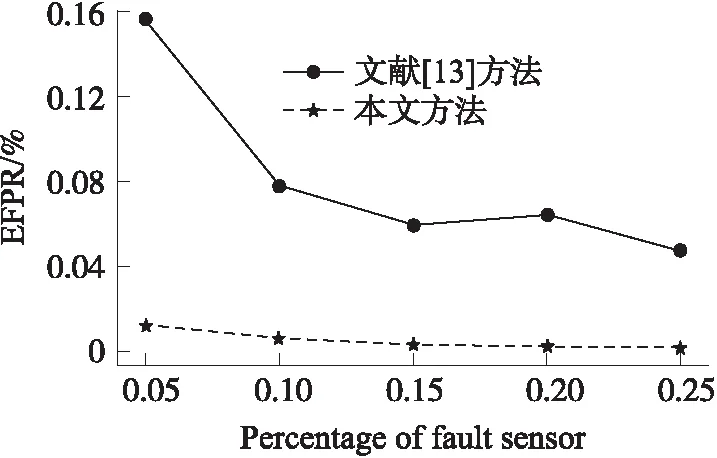
while(every ΔTtime andt′ Calculatingμ(γ)andξ if(μ(γ)<1 andr(t)!=r(t-1)){ ErrorCount+=1; } if(μ(γ)<ξorr(t)=r(t-1)){ FaultCount+=1; if(FaultCount>m/2){ broadcasting data to all neighbors } } if(μ(γ)>ξandr(t)!=r(t-1)){ EventCount+=1; } t′+=ΔT; } if(ErrorCount>2m/3); status=Error; if(FaultCount>2m/3); status=Fault; if(EventCount>2m/3); status=Event; 從時間復雜度和空間復雜度考慮,假設滑動窗口中的數據流規模為w,滑動窗口的大小為k,w>k。進行一次數據更新,滑動窗口有w-k次的數據輸入。每更新一次窗口就要重新計算置信區間,所以時間復雜度O(w-k),空間復雜度為O(k)。所以本文的算法即使在大規模的數據中也不會出現數據災難。 與采用WSN空間屬性的方法相比,本文只從WSN時間數據入手,沒有和鄰居節點交換信息,不產生額外的通信消耗。只有當節點即將發生故障的時候向鄰居傳播數據,以消耗少量的能量,提高算法的安全性。 為了對本文的算法進行定性的分析,引入節點的檢測率(True Positive Rate)和誤報率(False Positive Rate)[20]用來衡量算法的可靠性。 定義3事件節點檢測率(Event True Positive Rate ETPR)ETPR(C): (14) 定義4事件節點誤報率(Event False Positive Rate EFPR)EFPR(C): (15) 定義5錯誤節點檢測率(Fault True Positive Rate FTPR)FTPR(C): (16) 定義6錯誤節點誤報率(Fault False Positive Rate FFPR)FFPR(C): (17) 式中:Ev為實際事件節點集合,S為事件區域所有節點,Er為實際錯誤節點集合。 由于估計的置信區間存在精度偏差,有可能將正常節點識別為誤差節點,所以引入誤差節點誤識率。 定義7誤差節點誤識率(Error False Recogni-tion Rate EFRR)EFRR(C): (18) 式中:N為正常節點集合。 如前文所述樣本數k(滑動窗口大小)和置信度α的選擇會影響置信區間的估計值。樣本數太少會造成較大的偏差,影響算法的性能。由于傳感器節點空間資源有限,樣本不能太大否則會導致傳感器節點能源過快消耗。為了確定樣本數和置信度大小,本文通過實驗來進行選擇。 本文的實驗是在python2.7平臺上,n個傳感器均勻的部署在32a×32a的區域中。假設事件過程{r(t)}和錯誤隨機過程{r′(t)}分別滿足r(t)~N(μ,σ2)和r′(t)~U(En(t),Ee(t)),對?t,模擬實驗中取μ=100,σ=10。假設傳感器的采樣頻率為10 Hz,即ΔT=0.1s,Tth=1s,m=10。 實驗1 本實驗n=1024,錯誤節點占傳感器節點總數的10%。假設事件發生在(17,5)到(27,15)的11a×11a區域。α取值為95%或99%。實驗結果均取100次實驗結果的平均值,仿真結果如表2所示。 表2 不同樣本數和置信度下的實驗結果 隨著樣本數增加,同一個置信度下,檢出率總體先增加后減小,誤報率總體先減小后增加。在樣本數為30時有較好的檢測結果,為減小因置信區間估計導致的誤差節點誤識率EFRR(C),選擇樣本數為30,置信度為99%作為后續實驗的參數。 為驗證本文方法的效果并評估其性能與文獻[13]的方法進行對比實驗。 實驗2 比較本文的方法在不同規模,相同的錯誤節點(0.5%)下的性能。文獻[13]使用其論文描述的實驗參數δ=1.96,C=8。圖1為一次實驗的快照,圓點為錯誤節點。實驗結果如圖2~圖5所示。圖2和圖3為事件區域事件的檢測率和誤報率,圖4和圖5為錯誤節點檢測率和誤報率。本文采用WSN的時間屬性,所以在不同規模傳感器網絡下具有較高的事件檢出率和較低的事件誤報率,且錯誤節點同樣保持較高的檢測率和低的誤報率。實驗結果表明本文的方法在不同規模的傳感器網絡下算法穩定性高,受傳感器網絡規模影響小。 圖5 錯誤節點誤報率 圖1 一次模擬實驗快照 圖2 事件節點檢測率 圖3 事件節點誤報率 圖4 錯誤節點檢測率 實驗3 為了驗證不同錯誤節點下算法的穩定性,采用傳感器節點數量n=1 024,并和文獻[13]做比較。實驗結果如圖6~圖9所示。 圖6 事件節點檢測率 圖7 事件節點誤報率 圖8 錯誤節點檢測率 圖9 錯誤節點誤報率 圖6和圖7為事件區域事件檢測率和事件誤報率,實驗表明,即使隨著錯誤節點的增加,采用本文的算法還能保持較高的檢出率,而誤報率也不會隨著錯誤節點的增加而增加,這是因為本文采用WSN時間序列的數據,這樣可以減少因WSN空間錯誤節點影響而產生誤判的情況。 圖8和圖9為錯誤節點檢測率和誤報率,當錯誤節點增加時,傳感器節點的錯誤檢測率保持98%以上,誤報率保持0.5%以下。 本文從數據的時間相關性入手,只需少量的數據通過簡單的計算就能估計出較好的總體樣本區間,計算區間與數據的區間差異度實現異常來源的判斷,算法復雜度低,計算量小而且不產生額外的傳感器網絡通信,有效的延長了傳感器網絡的壽命。受傳感器網絡規模的影響小,在傳感器網絡錯誤節點增加的情況下仍保持較高的檢測率和較低的誤報率。 參考文獻: [1] Zhou Zhangbing,Xu Jiabei,Zhang Zhenjiang. Energy-Efficient Optimization for Concurrent Compositions of WSN Services[J]. IEEE Access,15 Sep 2017,PP(99):1-1,ISSN:2169-3536. [2] Bai X,Liu L,Cao M,et al. Collaborative Actuation of Wireless Sensor and Actuator Networks for the Agriculture Industry[J]. IEEE Access,2017,5(99):13286-13296. [3] Qiu T,Zhao A,Xia F,et al. ROSE:Robustness Strategy for Scale-Free Wireless Sensor Networks[J]. IEEE/ACM Transactions on Networking,2017,PP(99):1-16. [4] Ayadi H,Zouinkhi A,Boussaid B,et al. A Machine Learning Methods:Outlier Detection in WSN[C]//International Conference on Sciences and Techniques of Automatic Control and Computer Engineering. IEEE,2016:722-727. [5] Xu W,Gao H,Liu Y,et al. An Adaptive Spatial Outlier Detection Algorithm with no Parameter for WSN[C]//International Conference on Information Fusion. 2017:1-8. [6] Luo X,Dong M,Huang Y. On Distributed Fault-Tolerant Detection in Wireless Sensor Networks[J]. IEEE Transactions on Computers,2006,55(1):58-70. [7] Krishnamachari B,Iyengar S. Distributed Bayesian Algorithms for Fault-Tolerant Event Region Detection in Wireless Sensor Networks[J]. Computers IEEE Transactions on,2004,53(3):241-250. [8] 李桂丹,孫雨耕,劉麗萍,等. 分布式無線傳感器網絡容錯事件邊界檢測[J]. 計算機工程與應用,2009,45(17):28-32. [9] 魏暢,李光輝. 基于約簡策略與自適應SVDD的無線傳感網絡 離群檢測方法[J]. 傳感技術學報,2017,30(9):1388-1395. [10] 高建良,徐勇軍,李曉維. 基于加權中值的分布式傳感器網絡故障檢測[J]. 軟件學報,2007,18(5):1208-1217. [11] 費歡,李光輝. 基于K-means聚類的WSN異常數據檢測算法[J]. 計算機工程,2015,41(7):124-128. [12] 姜旭寶,李光耀,連朔. 基于變寬直方圖的無線傳感器網絡異常數據檢測算法[J]. 計算機應用,2011,31(3):694-697. [13] 曹冬磊,曹建農,金蓓弘. 一種無線傳感器網絡中事件區域檢測的容錯算法[J]. 計算機學報,2007,30(10):1770-1776. [14] 趙志剛,屈劍鋒. 基于WSN和置信區間計算的轉播機房溫控系統[J]. 計算機工程與應用,2011,47(30):219-223. [15] 李云飛. 極值分布參數基于不完全數據的區間估計[J]. 統計與決策,2015(13):81-83. [16] 陳圣兵,王曉峰. 基于樣本差異度的SVM訓練樣本縮減算法[J]. 計算機工程與應用,2012,48(7):20-22. [17] Datar M,Gionis A,Indyk P,et al. Maintaining Stream Statistics over Sliding Windows[J]. Siam Journal on Computing,2002,31(6):1794-1813. [18] Huber P J. Robust Statistics[J]. Journal of the American Statistical Association,1981,78(381):1248-1251. [19] Lee D W,Kim J H. High Reliable In-Network Data Verification in Wireless Sensor Networks[J]. Wireless Personal Communications,2010,54(3):501-519. [20] Fei H,Xiao F,Guang-Hui L I,et al. An Anomaly Detection Method of Wireless Sensor Network Based on Multi-Modals Data Stream[J]. Chinese Journal of Computers,2017,40(8):1829-1842.3.3 性能分析
4 實驗結果及分析
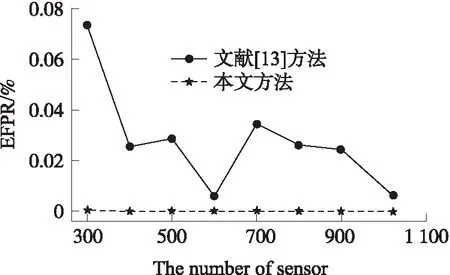
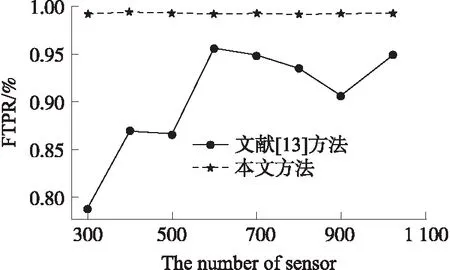
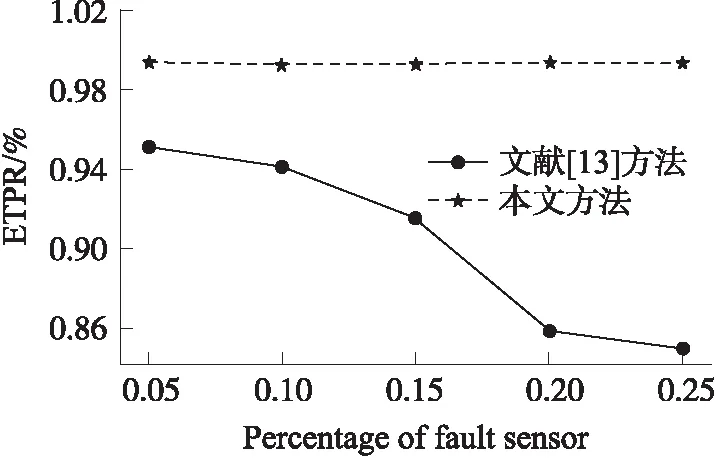
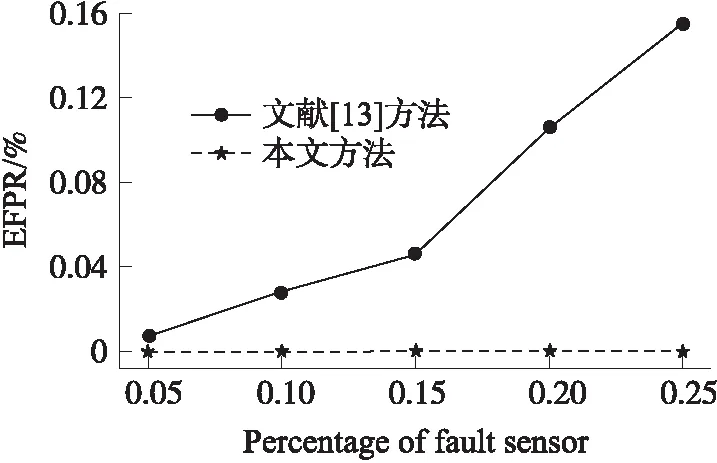

5 結語

