電容式傳感器測量用二極管雙T型交流電橋的分析

黃 帥，黃 偉，陳 琳，張雙銀，杜和萍

（ 1.銅仁學院 大數據學院，貴州 銅仁 554300；2.銅仁學院 材料與化學工程學院，貴州 銅仁 554300）

0．引言

電容式傳感器是將非電量的變化轉換為電容量的變化，從而實現對非電量的測量[1]。對電容量變化的測量是通過合適的調理電路將其轉化為與其成正比的電壓、電流或頻率進行的[2]，相應的調理電路有調頻電路、運算放大器、變壓器式交流電橋、二極管雙T型交流電橋、脈沖寬度調制電路等[3-6]。二極管雙T型交流電橋的優點是電路簡單，無需相敏檢波和整流電路，便可得到較高的直流輸出電壓。在“傳感器原理及實驗”課程所用的教材中僅給出了二極管雙T型交流電橋輸出電壓的近似結果，教學中會讓學生對此產生突兀和困惑。因此對該結果的來歷的詳細分析是很有必要的，是對教學內容的補充和完善。同時，后續相關科研項目的開展將采用二極管雙T型交流電橋對電容進行測量。為保證相關系統的準確性和可靠性，對二極管雙T型交流電橋輸出電壓的詳細推導和影響因素分析也是非常有必要的。本文將從電路基本原理和分析方法出發，詳細推導二極管雙T型交流電橋的輸出電壓，并分析相關電路參數對輸出電壓的影響。

1．理論分析

二極管雙T型交流電橋的電路由二極管VD1、VD2、電容C1、C2、電阻R1、R2、負載RL，以及周期方波信號u構成，如圖1（a）所示。方波信號u的周期為T，最大值和最小值分別為+U和-U，如圖1（b）所示。在u的正半周期，二極管VD2導通，VD1截止，忽略二極管上的壓降，等效電路如圖1（c）所示；由于充電電阻很小，對電容C2的充電很快就完成，因此等效電路又可簡化為圖1e）所示電路，其中電容C1的初始電壓UC1_0（在圖示參考方向下，其值為-U）可由負半周的等效電路分析得到。同理，在u的負半周期，二極管VD1導通，VD2截止，等效電路如圖1（d）所示；等效電路又可簡化為圖（1f）所示電路，在圖示參考方向下電容C2的初始電壓UC2_0=-U，可由正半周的等效電路分析得到。

對圖1e）應用網孔電流法[7]，可得電路方程組如式（1）～式（3）所示。

附加電容C1的初始條件如式（4）所示。

聯立式（1）-（4）式，即可求出電路的解。

由式（1）可得出I12，如式（5）所示。

將式（5）代入式（2）得出I11，如式（6）所示。

將式（3）代入式（6）得到關于UC1的微分方程，如式（7）所示。

則式（7）化簡為式（7′）。

求解式（7′）得出UC1，如式（8）所示。

式（8）中A、B為待定常數。分析圖1e）的電路可知，當時間t→∞，電容C1兩端的電壓與電阻RL兩端的電壓URL_∞相等，而URL_∞又等于電阻R2與RL串聯回路在RL上的分壓，如式（9）所示。

將電容的初始條件式（4）代入式（8），并利用B=1，得出系數A，如式（10）所示。

則UC1可表示為式（11）所示。

將式（11）代入式（3）可得電流I11，如式（12）所示。

利用式（5）及式（12），在正半周期電阻RL兩端的電壓可表示為式（13）所示。對式（13）在正半周期內積分，可得RL兩端的平均壓降，如式（14）所示。

同理，對圖1f）應用網孔電流法，附加電容C2的初始條件，可得電路方程組，如（15）-（18）式所示。

聯立式（15）～式（18）可求得在負半周期電阻RL兩端的電壓，如式（19）所示：

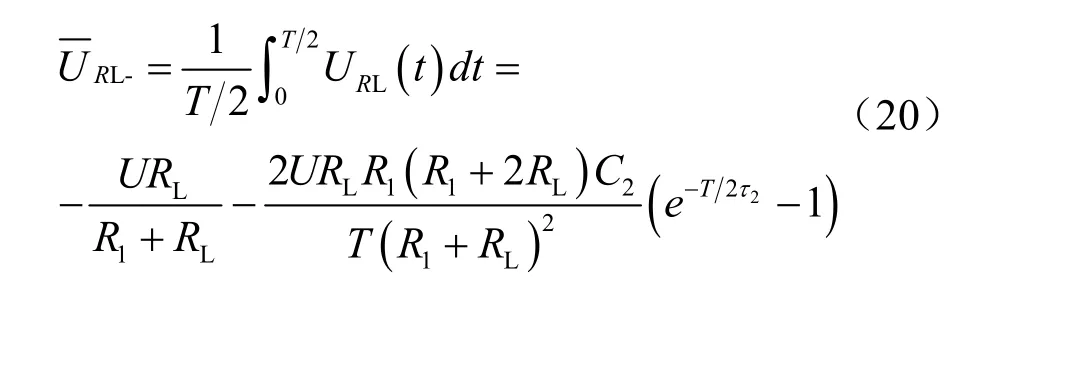
圖1 二極管雙T型交流電橋 (a)電路構成，(b)周期信號，(c)信號正半周期等效電路，(d)信號負半周期等效電路，(e)信號正半周期簡化電路，(f)信號負半周期簡化電路Fig.1 Diode-double-T-type alternating current bridge

由式（14）和式（20）可得在一個信號周期內電阻RL兩端的平均電壓，如式（21）所示。

2．電路參數對輸出電壓的影響

在式（21）第一項中對負載RL求導數，并令其等于零，可得RL=R1時，該項絕對值取最大值（因其對RL的二階導數小于零）為因此，為減小與待測電容無關的輸出項，應盡可能的使R2=R1，工程應用時R2、R1應選用同一廠家同一批次的產品，或在R2或R1的支路上串聯一個可變電阻來調節實現。如若不能實現R2=R1，則應選擇R2、R1使其遠離RL。

式（21）中第二項與各電路參數的關系較為復雜，后續討論將基于前面的結論作簡化分析。考慮n=1，則式（21）可簡化為式（22），時間常數則簡化為式（23）。

當信號周期遠大于電容充放電的時間常數，即T?τ1,τ2時，，，則在整個信號周期內電阻RL兩端的平均電壓如式（24）所示，這正是教材中給出的近似結果，它與兩個電容的差值成線性關系。

式（24）中f=1/T，為周期信號的頻率。式（24）對R1、RL的導數均大于零，二階導數均小于零，即是說電阻RL兩端的平均電壓隨電阻R1、RL的增大而增大，但增大的速率減小。同時其隨信號頻率的增大而增大，即要求周期越小越好。但R1、RL的增大會導致τ1、τ2增大，使Tτ1,τ2不滿足，式（24）就不成立。在式（23）中，RL趨近于0時，τ1=R1C1、τ2=R1C2；RL趨近于∞時，τ1=2R1C1、τ2=2R1C2。因此，時間常數主要取決于R1與C1或C2的乘積，RL對其影響不大。

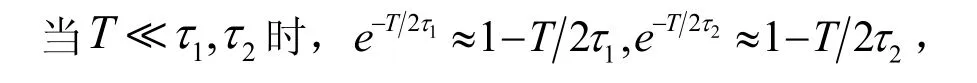
則在整個信號周期內電阻RL兩端的平均電壓如式（25）所示，結果為零。其原因為脈沖電壓源的頻率過高，電容電壓來不及變化，電容上儲存的電荷就不能通過電阻RL釋放，導致電阻RL兩端的平均電壓與電容值無關。

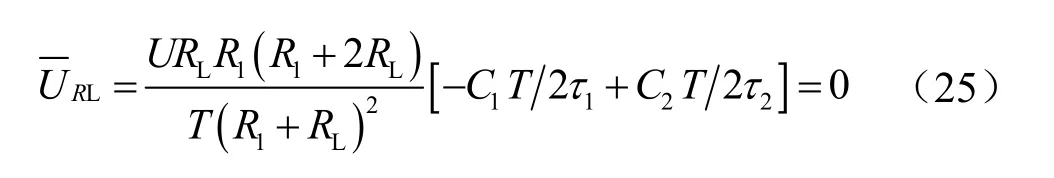
綜上所述，脈沖電壓源的頻率過低，電阻RL兩端的平均電壓很小；頻率過高，電阻RL兩端的平均電壓為零。在實際工程應用時，應根據被測電容的大小，選擇合適的電阻R1，在保證激勵信號的周期遠大于時間常數τ1、τ2的條件下，盡可能地的提高信號頻率，可獲得更大的輸出電壓。

3．結論

從基本的電路理論和分析方法對二極管雙T型交流電橋輸出電壓作了詳細的推導，是對“傳感器原理及實驗”課程中有關二極管雙T型交流電橋部分的內容的補充和完善，能讓學生透徹的理解近似結果的來歷。同時，詳細分析了相關電路參數對輸入電壓的影響，為后續相關項目的開展過程中采用二極管雙T型交流電橋對電容進行測量的電路設計提供了技術參考。為保證調理電路獲得盡可能大的輸出電壓，設計時應根據被測電容的大小，選擇合適的電阻R1，在保證激勵信號的周期遠大于時間常數τ1、τ2的條件下，盡可能提高信號頻率。

參考文獻：

[1]胡向東．傳感器與檢測技術[M]．北京：機械工業出版社，2013：75．

[2]佘生能，孫士平．電容傳感器新型電容測量電路設計[J]．中國測試技術，2005，31（5）：42-43．

[3]趙樹忠，安曉星．平板電容式液體介電常數測試系統[J]．山東工業技術，2016（1）：178-179．

[4]邵學濤，李新娥．振蕩式微小電容測量電路[J]．電子測試，2011（1）：50-53．

[5]黃雨濛，戚昊琛，胡智文，等．MEMS電容式壓力傳感器檢測電路比較研究[J]．電子科技，2015，28（1）：186-189．

[6]孫杰．電容式加速度傳感器檢測電路的設計與研究[D]．上海：復旦大學，2013：32-42．

[7]王雷，王保良，冀海峰，等．電容傳感器新型微弱電容測量電路[J]．傳感技術學報，2002（4）：273-277．

[8]李瀚蓀．電路分析基礎（上冊）[M]．北京：高等教育出版社，2006：62-68．