混合測量子空間聚類算法的研究

金利英, 趙升噸

(西安交通大學機械工程學院, 710049, 西安)

子空間聚類算法是模式識別和數據挖掘等應用領域的重要工具,隨著新技術的高速發展,應用環境不斷變化,大規模數據與復雜結構數據對子空間聚類算法的需求越來越緊迫。迄今為止,已開發出許多聚類算法[1-2],以實現數據聚類的任務,這些算法在如何定義集群以及如何識別集群方面有很大的不同。K-means算法是最經典且應用最廣的聚類算法之一[3],但對聚類中心的初始化非常敏感,影響聚類結果和收斂速度。Huang等在K-means算法的基礎上提出了權重K-means算法(WK-means)[4],為每個特征分配一個權重,特征權重與特征尺度因子相關[5]。使用閔可夫斯基距離自動計算每個集群的特征權重,以確保這些權重可以看作是特征調節因子。

現有的大多數子空間聚類算法僅使用一個距離函數來評估各個樣本之間的距離,該距離函數難以處理具有復雜內部結構的數據集。通過特征之間權重方向旋轉特征空間可進一步提高聚類性能,在向量空間模型中[6],余弦相異性比歐式距離更重要。在特征空間(ESCHD)中[7],余弦相異性可提高軟子空間聚類的性能。

受iMWK-means和ESCHD算法的啟發,本文提出了混合測量子空間聚類算法(iMWK-HD)。該算法將余弦相異性引入到距離函數中,使閔可夫斯基指數與分配特征權重指數相符,構造新的目標函數。使用該目標函數推導迭代過程中更新規則,促進特征空間的擴展、收縮和旋轉,iMWK-HD算法可提高聚類精度和聚類結果的穩定性。

1　iMWK-HD算法

1.1　閔可夫斯基距離和智能K-means算法初始化類中心

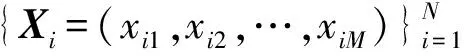
(1)

式中:β為用戶定義的參數,表示權重對距離貢獻的影響率。d(xi,xj)因β值的不同而變化,指數β≠2不再是特征比例因子。Huang等擴展了相應的閔可夫斯基測量[4],用于測量距離,以確保閔可夫斯基指數與特征權重指數一致。

智能K-means初始化[8](iK-means)是在運行K-means算法之前找出異常集群,即對數據集進行全局加權距離的計算并排序,取最大距離樣本點為異常集群,將其設置為初始類中心,在迭代過程中找出距離它最近的樣本點,然后從數據集中依次取出;在剩余數據集里取距離最遠的樣本為初始化類中心,在迭代過程中找出距離它最近的樣本點,然后從這個數據集里移出;依次類推,直到剩余數據集為空,之后選取樣本點個數最多的異常簇的異常集群為類中心。

1.2　混合測量

基于距離測量準則,在處理高維樣本點時會出現維數災難的情況[9],影響聚類結果的穩定性。將余弦相異性代入優化目標函數中,結合距離計算樣本點之間的距離,可促進特征空間轉換,樣本點xi和第j維k類中心vk之間的距離定義為

(2)

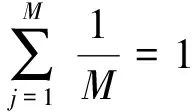
混合測量參數較少、易于實現,可控制數據集在特征空間中的形狀、大小和方向,能減小冗余和無關特征對數據集的影響,進而區分特征在不同子空間中的權重大小,提高全局搜索能力。

1.3　目標函數設計

目標函數是評估聚類性能的重要指標,直接影響算法的搜索方向和收斂速度。假設有N個M維數據集X={X1,X2,…,XN},第i個樣本點表示為Xi=(xi1,xi2,…,xiM);聚類中心矩陣V={v1,v2,…,vC},C是N個數據集劃分類數。利用混合測量求解目標函數最小值,定義為

(3)

式中:矩陣V=[vkj](1≤k≤C,1≤j≤M)為第k類在第j維特征上的類中心值;集群U=[uik](1≤i≤N,1≤k≤C)為第i個樣本對第k類的隸屬度;矩陣W=[wjk](1≤j≤M,1≤k≤C)為第j維特征對第k類的重要度。

iMWK-HD算法優化目標函數,矩陣U、W的最優解可由下式給出,即

(4)

(5)

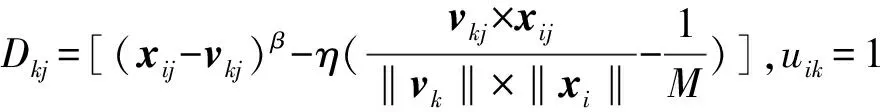
矩陣V的求解可由文獻[5]中iMWK-means算法進行迭代更新。式(3)的無約束最小化為

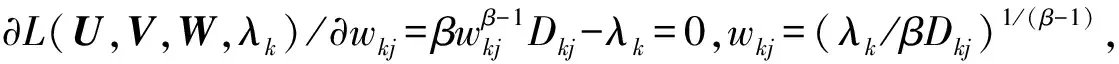
β∈{1.2,2.0,2.3,2.7,3.0,4.9},η∈[0,10],ε=10-5,G=500

iK-means initializeVandWwithwjk=1/M

fort=1:G

UpdataUt+1according to (4) withWtandVt;

UpdataVt+1according toWtandUt+1;

UpdataWt+1according to (5) withUt+1and

Vt+1;

Calculate the objective functionJ(Ut+1,Vt+1,Wt+1) with (3);

if |J(Ut+1,Vt+1,Wt+1)-J(U,V,W)|<εbreak;

End for

OutputWt+1,Vt+1andUt+1。

2　實驗設計和結果分析

實驗環境為Intel(R) Core(TM) i3-4170 CPU,Windows7,軟件開發平臺是Matlab 13.0。為驗證iMWK-HD算法有效性,與現有的iK-means,iWK-means和iMWK-means算法進行對比。

通過以上對于孟子武德思想的分析與歷史經驗的側證，我們可以看到，孟子以“仁者無敵”為核心的武德觀，因其精神化理想化的趨向和立意的高標，在國家國際的層面無法得到落實而為荀子所倡的武德原則所取代。而至于共同體與個人的層面，因具有共同追求或現實制度作為基本保障，孟子的武德思想煥發了生命力，具有無窮的魅力。孟子將直接的暴力置換為王霸之辯、天爵人爵之辯、批判精神、大丈夫人格與浩然之氣，面對沖突和矛盾，拒絕茍且或殘暴而指出向上一路。孟子亦被譽為“中國歷史上最有使命感的文化斗士，最有生命力的衛道圣雄”[12](P365)。

2.1　實驗數據和評估指標

選取UCI數據庫[10]中Wine、Hepatitis、Australian、Liver、Wave、Sonar、Musk這7個數據集來進行對比實驗,其基本信息如表1所示。在實驗中,使用精確度ACC[11]和RI[12]指標來評估聚類結果的性能,RI定義為

式中:T為在同一類的一對樣本點被分到同一類內;E為不在同一類的一對樣本點被分到不同的類里;F為不在同一類的一對樣本點被分到同一類內;P為在同一類的一對樣本點被分到不同類里。ACC、RI取值范圍為[0,1],數值越接近1,說明聚類性能越好。

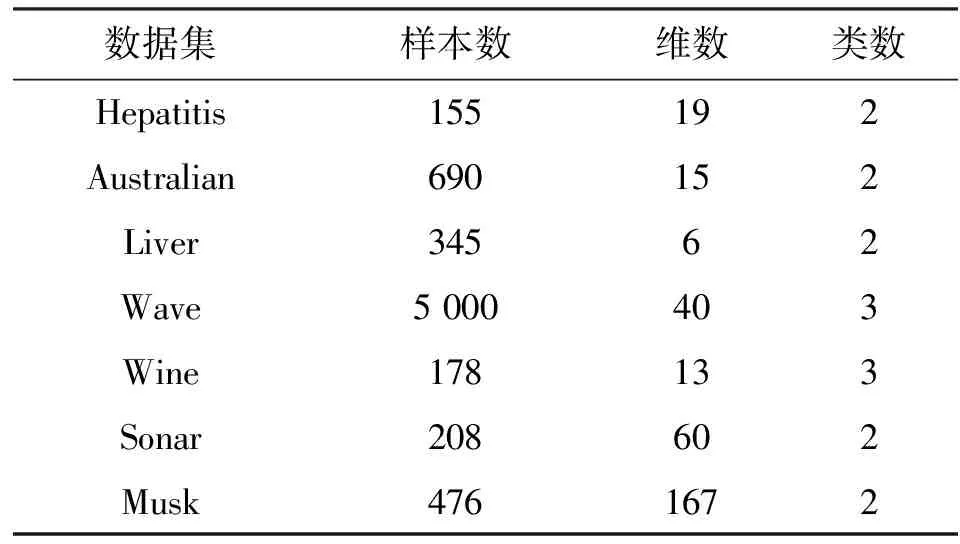
表1　數據描述

2.2　實驗結果和分析

算法對7個數據集聚類的最優精度、最優解如表2、表3所示。iMWK-HD算法和iMWK-means算法之間是閔可夫斯基指數β取相同值時對數據集進行實驗比較,表中平衡系數η為iMWK-HD算法獲得最優實驗結果時的取值。

由表2、表3可知:iMWK-HD算法在7個數據集上均獲得最優的ACC、RI,高出其他3種算法數個百分點;在聚類結果的穩定性、聚類精確度上,iMWK-HD算法更具優勢。這是因為本文將閔可夫斯基距離、余弦相結合構成新的目標函數,使其更好評價特征子集的質量,能更好找到子空間的內部結構,促進樣本在特征空間轉換,提高全局搜索能力,從而獲得更好的聚類結果。

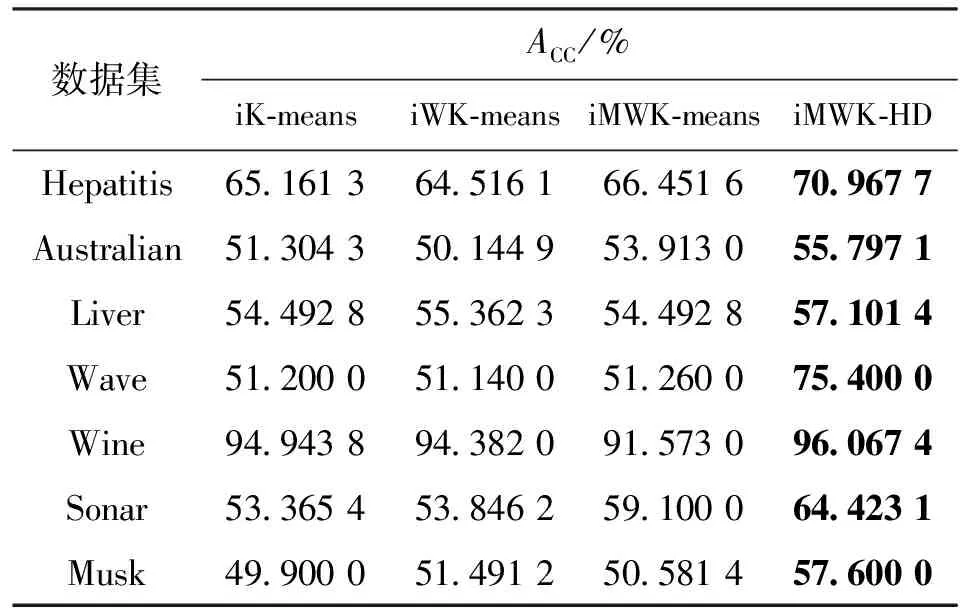
表2　算法對7個數據集聚類的最優精度

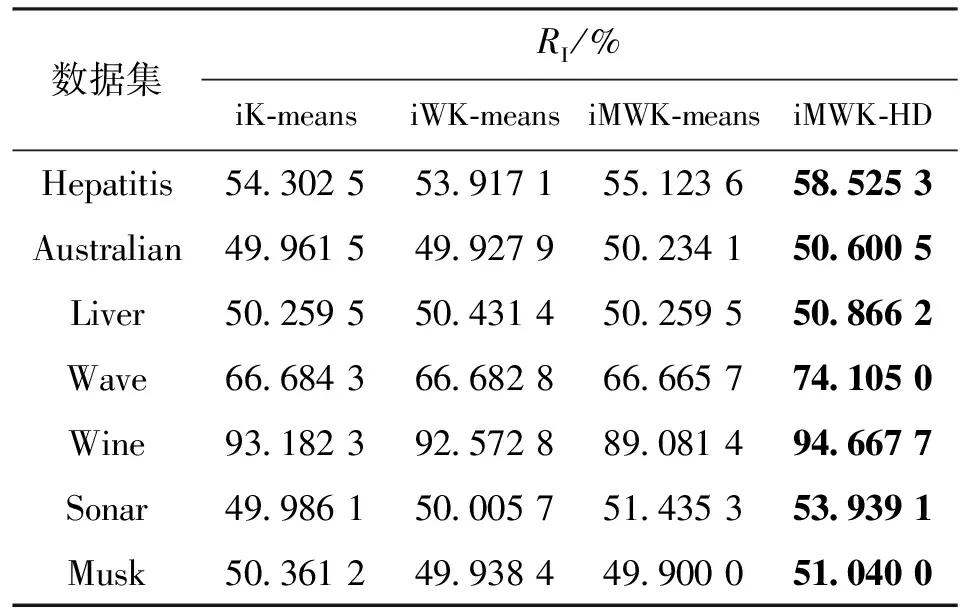
表3　算法對7個數據集聚類的最優解

β、η是iMWK-HD算法的重要參數,對于大規模數據Wave、高維數據Musk,在β取不同值時實驗獲得的ACC隨η的變化趨勢如圖1、圖2所示。

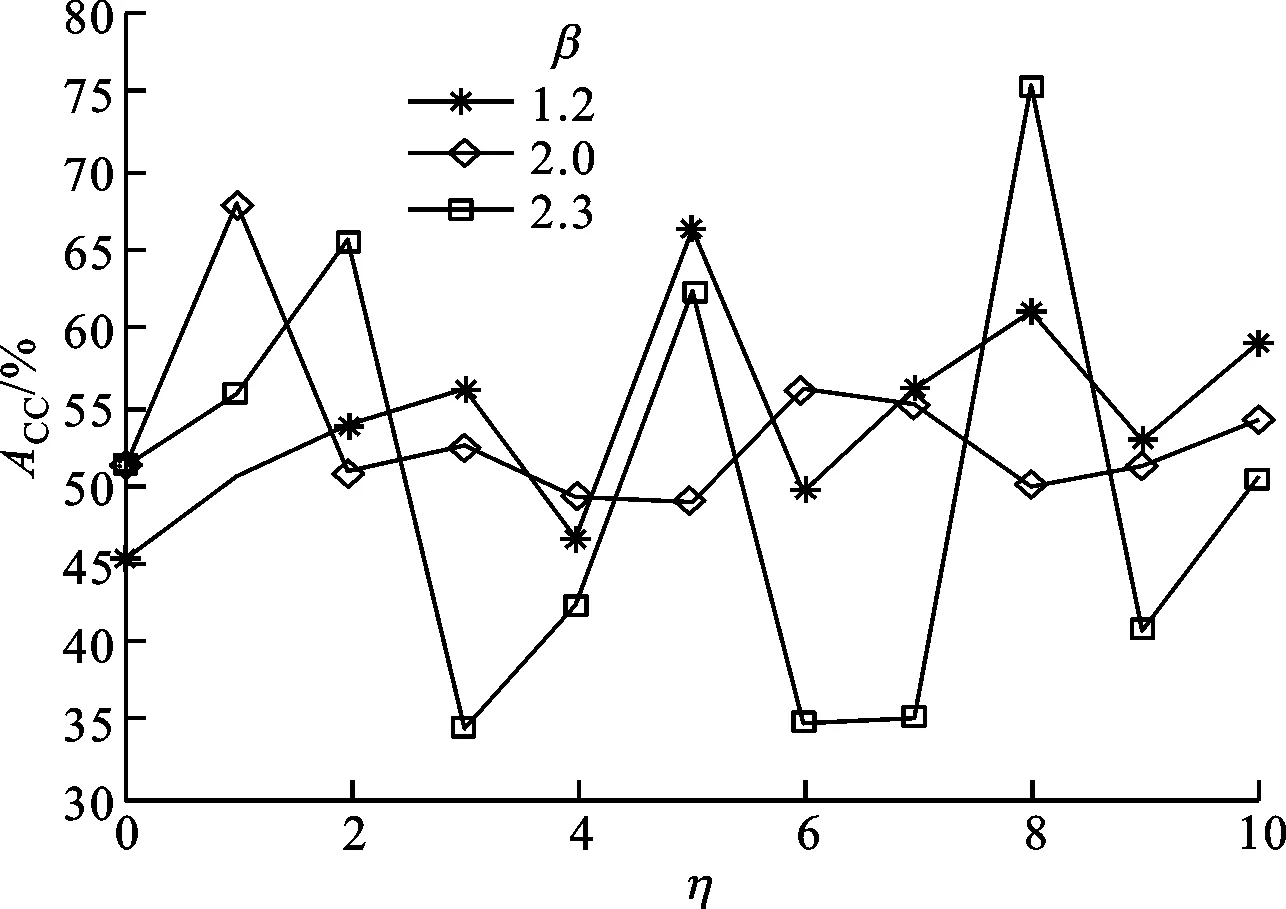
圖1　iMWK-HD算法在β=1.2,2.0,2.3時的聚類結果

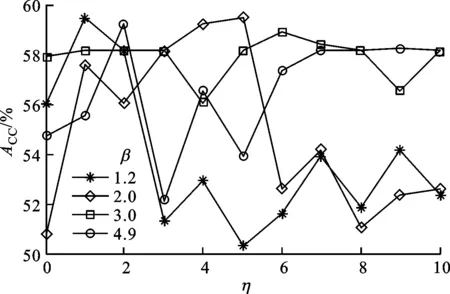
圖2　iMWK-HD算法在β=1.2,2.0,3.0,4.9時的聚類結果

由圖1中可知,當β=1.2,2.0時,ACC隨著平衡系數η的不同取值而變化,且絕大多數ACC優于未引入余弦時的聚類結果,說明引入余弦可增強算法的魯棒性;當β=2.3且η=3,4,6,7,9,10時,ACC低于η=0時的值,說明對大規模數據而言,β在2.3以內引入余弦能很好地調節特征權重因子,促進特征空間轉換,從而提高聚類精確度;當η=0且β分別取1.2、2.0、2.3時,實驗獲得的ACC分別為45.1%、51.1%、51.3%;當η=1時,ACC分別為50.5%、68%、55.8%;當η=2時,ACC分別為53.7%、50.7%、65.4%;當η取定值時,在β取值范圍內,實驗獲得的ACC與β取值無關,這說明余弦的引入與β不沖突。

由圖2中可知,當β=1.2時,ACC隨著η的不同取值而變化,且當η=3時,ACC均小于η=0時的值,說明余弦的引入在β=1.2時的聚類結果不穩定。當β=2.0,3.0,4.9時,大部分ACC優于未引入余弦時的聚類結果,對于高維數據,β取值大于2.0時余弦的引入能很好調節特征權重因子,促進特征空間轉換,從而提高聚類ACC和算法的魯棒性。因此,iMWK-HD算法在原子空間聚類算法參數下,有且僅增加一個控制參數η,能最大程度保證算法在高維數據中的聚類精度和聚類結果的穩定性。

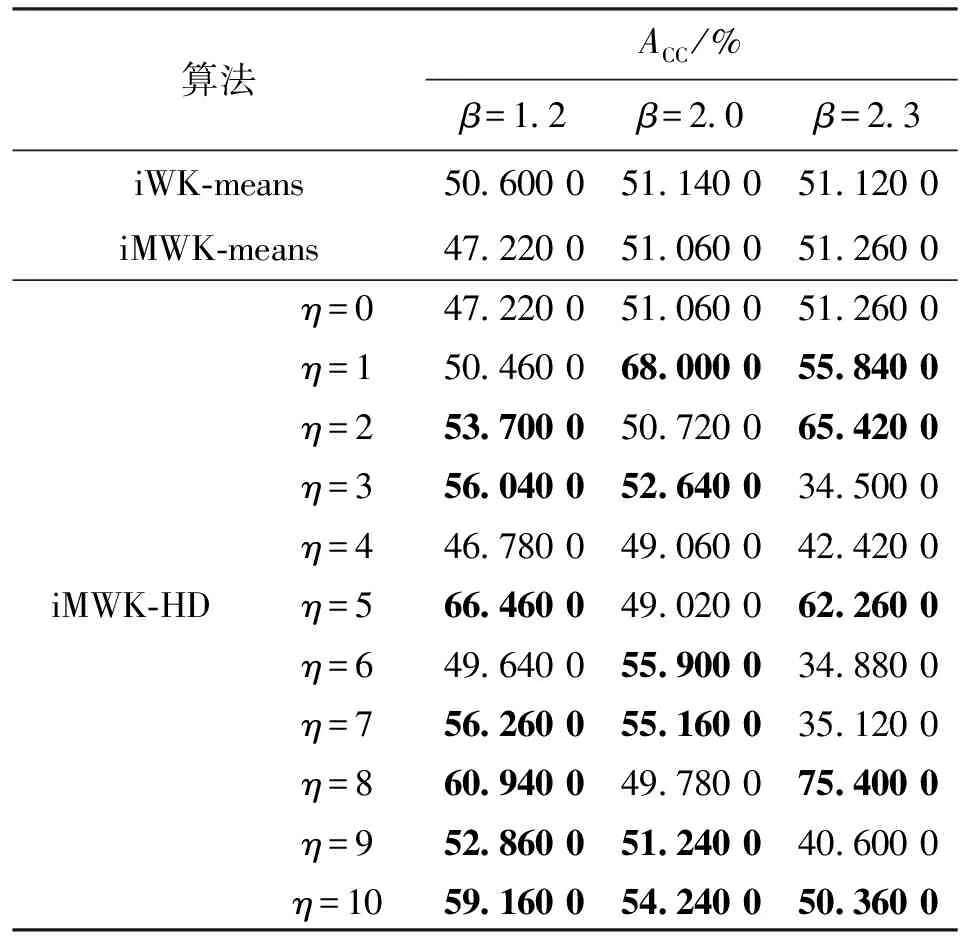
表4　Wave數據集精確度ACC

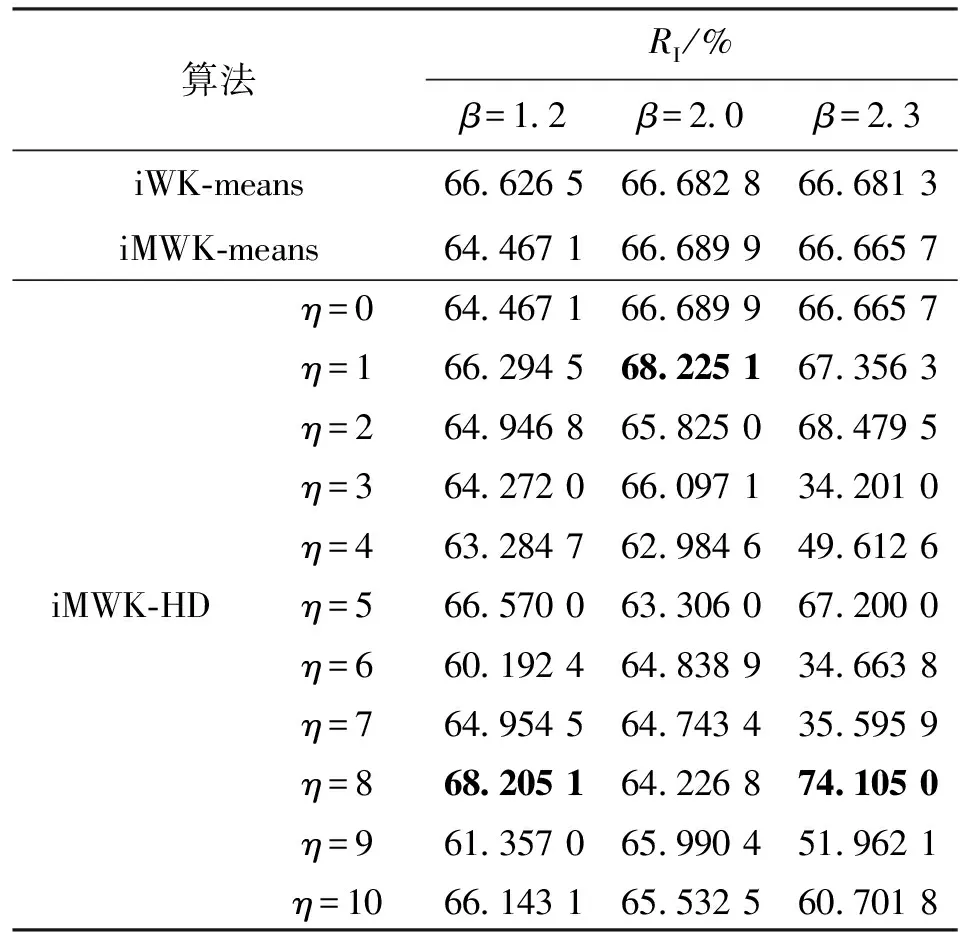
表5　Wave數據集RI

由表4、5可知,當β=1.2,2.0且η=0,即未引入余弦時,iWK-means算法取得ACC最優值,但iMWK-HD算法的ACC與最優結果相差不大,而引入余弦時,iMWK-HD算法的ACC大部分優于iWK-means和iMWK-means算法。當β=2.3且η=0時,iMWK-HD和iMWK-means算法的ACC相同;而引入余弦時,iMWK-HD算法的最優值高出iWK-means和iMWK-means算法分別為24.24%、24.1%,說明iMWK-HD算法具有較強魯棒性和較高聚類精度。ACC所示的最佳聚類性能并不總是與RI表示一致,因此有必要對不同指標聚類算法的性能進行評估。

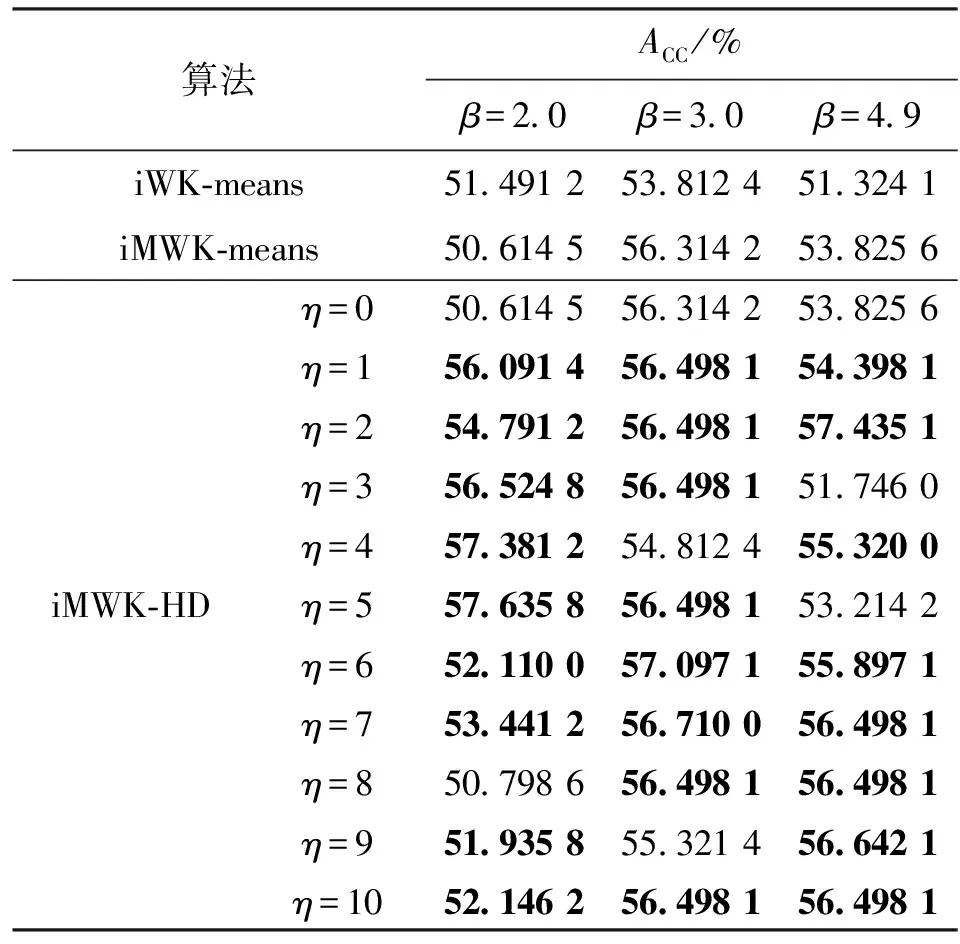
表6　Msuk數據集精確度ACC

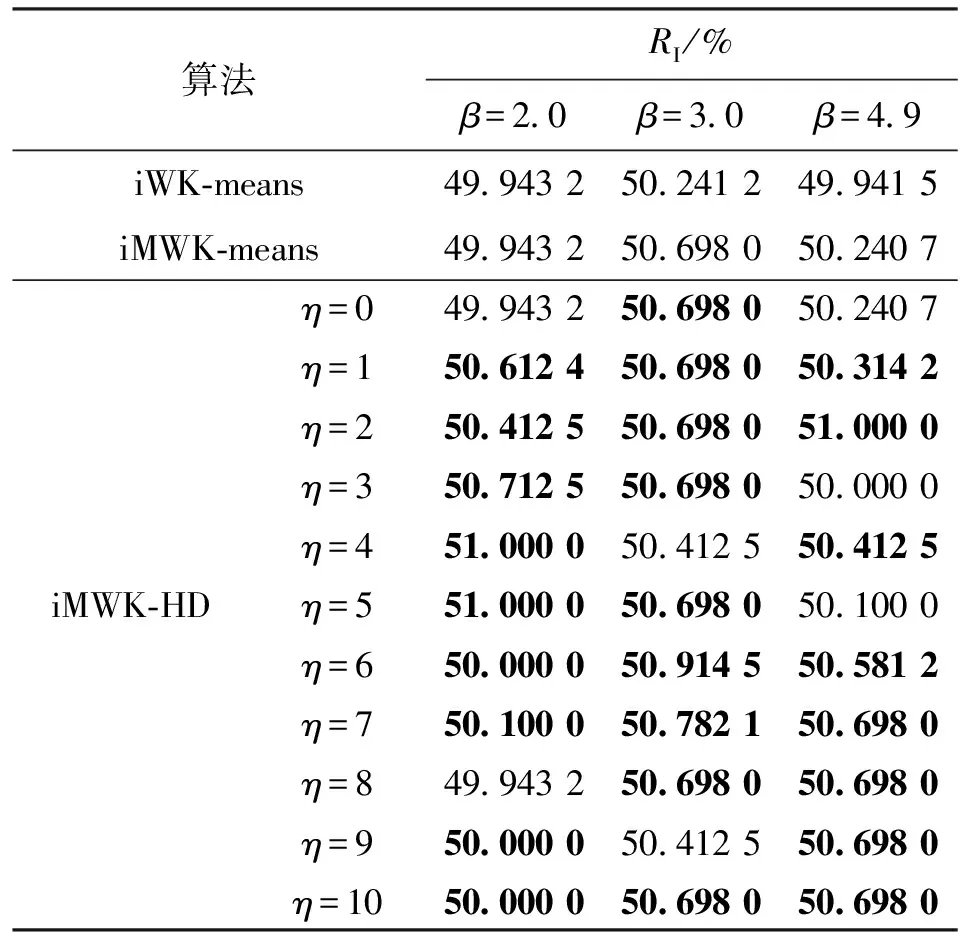
表7　Msuk數據集RI

由表6可知,當η=0,即未引入余弦時,iMWK-HD和iMWK-means算法在β取不同值時ACC、RI均相同;當引入余弦時,iMWK-HD算法在大多數情況下的實驗結果均優于iMWK-means和iWK-means算法,只有少數實驗結果低于它們,且實驗結果相差不大,說明本文所提iMWK-HD算法具有較強魯棒性。Musk數據雖擁有較高維數,iMWK-HD算法也能有效地提取對應維數信息,再一次體現出iMWK-HD算法的聚類結果穩定性好、聚類精度高的優點。

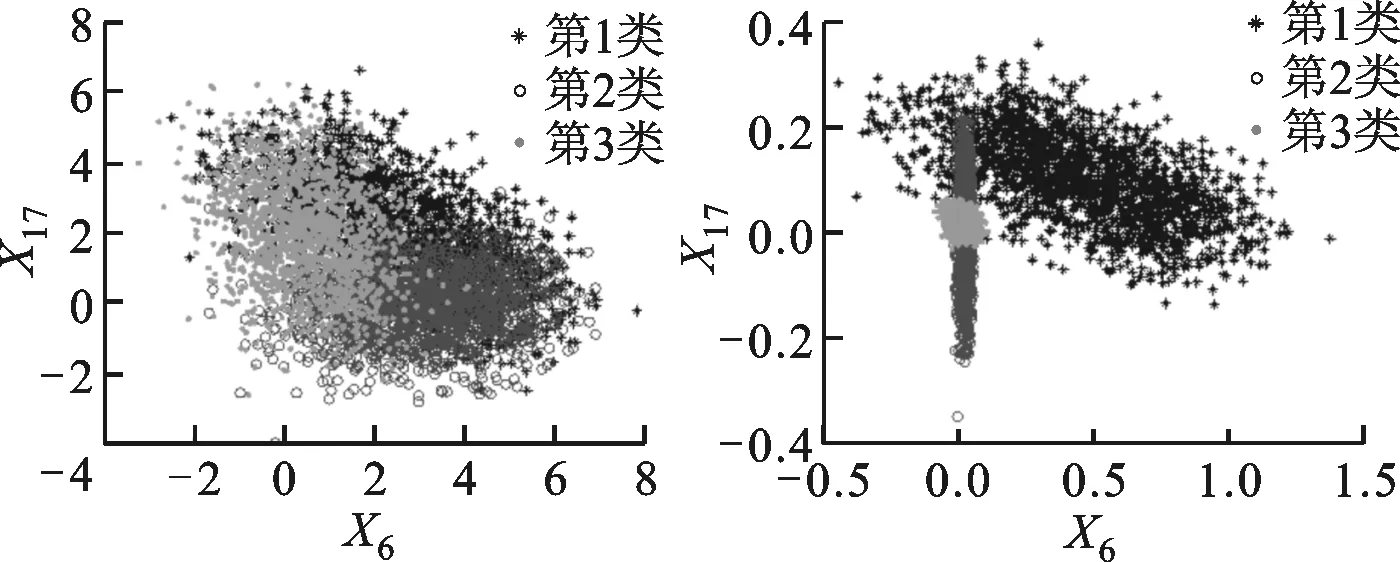
(a)原始數據分配　　　(b)iMWK-HD算法

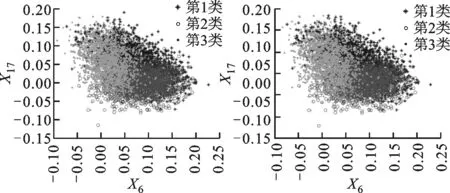
(c)iMWK-means算法　　(d)iWK-means算法圖3　　　　Wave數據集中3種算法根據特征權重進行轉換的數據分布情況

3種算法根據特征權重進行轉換的數據分布情況如圖3、圖4所示。由圖3、圖4可知,集群之間的重疊較少,在總體性能上優于另外兩種算法,說明iMWK-HD算法聚類結果的穩定性好。這是因為iMWK-HD算法的目標函數中引入了余弦相異性,使特征權重在特征空間不僅能擴展、收縮,還能旋轉,iMWK-HD算法能有效提高解的質量。

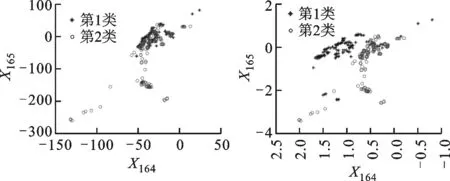
(a)原始數據分配　　　(b)iMWK-HD算法

(c)iMWK-means算法　　(d)iWK-means算法圖4　Musk數據集中數據分布情況

對比實驗結果說明了本文所提iMWK-HD算法的魯棒性及聚類結果的穩定性。子空間聚類算法能更好發現子空間的內部結構,展現良好的聚類結果。對于Wine數據,各個子空間聚類算法的內部結構如表8所示,將其各維標上對應編號。由表8中前6位特征重要性排序可知,所得各個數據簇的特征排列順序在每個子空間聚類算法中有所不同,也可在其他數據集中得到類似發現,這種發現子空間的能力可提高聚類有效性。

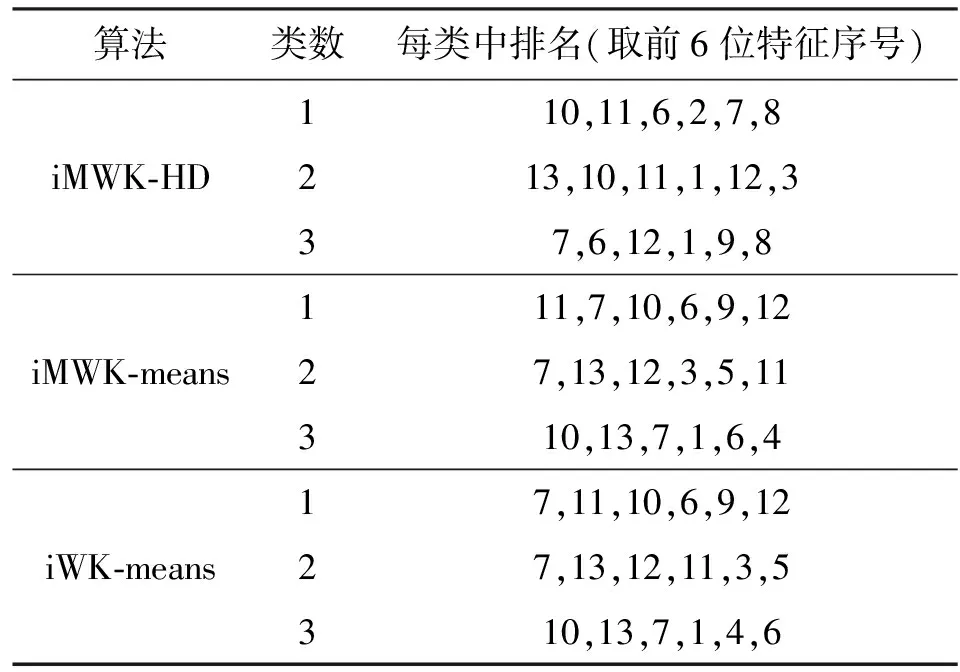
表8　Wine數據集上的特征重要性排序

綜上對比實驗結果,分析iMWK-HD算法最優的原因:①初始化階段使用智能K-means算法求解聚類中心點,解決了隨機選取類中心導致若干聚類合并及正確選擇類數的問題;②混合測量導出樣本與中心點的距離,解決了特征空間旋轉問題;③利用拉格朗日乘子求解新的隸屬度和特征權重迭代更新公式,保證了類中心的穩定性,從而促進特征空間轉換,獲取有效的聚類結果。實驗結果驗證了iMWK-HD算法的優越性。

3　結　論

本文提出了一種混合測量子空間聚類算法,該算法是在iMWK-means框架下,將余弦相異性引入到子空間聚類的目標函數中,與閔氏距離相結合,構造了新的目標函數,該目標函數控制參數少,易于實現;利用拉格朗日乘子求解樣本點新的隸屬度和特征權重迭代更新距陣,實現特征權重因子自動調節,促進特征空間轉換,從而有利于隸屬度矩陣U的劃分和類中心矩陣V的精準度,最終獲取樣本點的最優聚類結果,提高聚類性能。實驗結果表明,與iK-means、iWK-means和iMWK-means三種算法相比,iMWK-HD算法聚類結果穩定性好,聚類精確度高。

參考文獻:

[1]PAN Y, WANG J, DENG Z. Alternative soft subspace clustering algorithm [J]. Journal of Information & Computational Science, 2013, 10: 3615-3624.

[2]CHEN X, YE Y, XU X, et al. A feature group weighting method for subspace clustering of high-dimensional data [J]. Pattern Recognition, 2012, 45: 434-446.

[3]MACQUEEN J. Some methods for classification and analysis of multivariate observations [J]. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, 1967, 1: 281-297.

[4]HUANG Z, NG M K, RONG H, et al. Automated variable weighting in k-means type clustering [J]. IEEE Transactions on Pattern Analysis and Machine Learning, 2005, 27(5): 657-668.

[5]RENATO C D, MIRKIN B. Minkowski metric, feature weighting and anomalous cluster initializing in K-Means clustering [J]. Pattern Recognition, 2012, 45: 1061-1075.

[6]KIM D. Group-theoretical vector space model [J]. International Journal of Computer Mathematics, 2015, 92(8): 1536-1550.

[7]WANG L, HAO Z, CAI R, et al. Enhanced soft subspace clustering through hybrid dissimilarity [J]. Journal of Intelligent & Fuzzy Systems, 2015, 29: 1395-1405.

[8]CHIANG M M, MIRKIN B. Intelligent choice of the number of clusters in k-means clustering: an experimental study with different cluster spreads [J]. Journal of Classification, 2010, 27(1): 1-38.

[9]PARSONS L, HAQUE E, LIU H. Subspace clustering for high dimensional data: a review [J]. ACM Sigkdd Explorations Newsletter, 2004, 6(1): 90-105.

[10] DENG Z, CHOI K S, CHUNG F L, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information [J]. Pattern Recognition, 2010, 43(3): 767-781.

[11] HUANG J Z, XU J, NG M, et al. Weighting method for feature selection in k-means [J]. Computational Methods of Feature Selection, Chapman & Hall/CRC, 2007, 193-209.

[12] RAND W M. Objective criteria for the evaluation of clustering methods [J]. Journal of the American Statistical Association, 1971, 66: 846-850.

[本刊相關文獻鏈接]

蘭進,徐亮,馬永浩,等.實驗研究類螺紋孔旋流沖擊射流的冷卻特性.2018,52(1):8-13.[doi:10.7652/xjtuxb201801 002]

韓樹楠,張旻,李歆昊.高容錯(2,1,m)卷積碼快速盲識別方法.2017,51(12):28-34.[doi:10.7652/xjtuxb201712005]

姜洪權,王崗,高建民,等.一種適用于高維非線性特征數據的聚類算法及應用.2017,51(12):49-55.[doi:10.7652/xjtuxb201712008]

曹巖,韋婉鈺,喬虎,等.采用設計結構矩陣的突發事件擴散預測及建模方法.2017,51(12):68-75.[doi:10.7652/xjtuxb 201712011]

王瑞琴,高炎,晏鑫,等.燃氣透平尾緣開縫區冷卻性能的非定常研究.2017,51(12):98-103.[doi:10.7652/xjtuxb201712 015]

程傳奇,郝向陽,李建勝,等.融合改進A*算法和動態窗口法的全局動態路徑規劃.2017,51(11):137-143.[doi:10.7652/xjtuxb201711019]

黃興旺,曾學文,郭志川,等.采用改進二進制蝙蝠算法的任務調度算法.2017,51(10):65-70.[doi:10.7652/xjtuxb2017 10011]

舒帆,屈丹,張文林,等.采用長短時記憶網絡的低資源語音識別方法.2017,51(10):120-127.[doi:10.7652/xjtuxb2017 10020]

曹衛權,褚衍杰,李顯.針對機器學習中殘缺數據的近似補全方法.2017,51(10):142-148.[doi:10.7652/xjtuxb201710 023]