采用不同管排組合的換熱器彈性管束殼程流體誘導振動響應

季家東, 葛培琪, 畢文波, 劉萍

(1.安徽理工大學機械工程學院, 232001, 安徽淮南; 2.山東大學機械工程學院, 250061, 濟南)

彈性管束換熱器[1-3]利用內部流體所誘導的彈性管束振動,在實現不同溫度的殼程、管程流體間強化傳熱的同時,為無源強化傳熱技術在換熱器中的應用開辟了新的研究方向[4-5]。高效彈性管束換熱器的設計應遵循的準則[6]是:在滿足強化傳熱的參數范圍內,對彈性管束的振動進行合理激發和有效控制,同時兼顧管束的疲勞壽命,確保其在強化傳熱的同時能長期運行不致破壞。這樣,對彈性管束在殼程或管程流體誘導下的振動響應機理進行深入研究就成為高效彈性管束換熱器設計的關鍵[6]。彈性換熱器內的流體誘導振動是一個復雜的流固耦合問題,而現階段的相關研究大多采用實驗手段,具有很大的局限性[7]。對于換熱器內多排彈性管束在殼程流體誘導下的振動響應進行分析,對進一步研究強化傳熱機理、改進管束結構及實現振動的合理激發和有效控制等都具有重要意義。

基于彈性管束換熱器的工作原理,閆柯等對一種新型空間錐螺旋彈性管束進行了數值模擬和實驗研究,發現在一定流速條件下,新型空間錐螺旋彈性管束的振幅增加緩慢,當流速超過某一值時,振幅隨著流速的增加而迅速增大,而空間錐螺旋彈性管束的模態頻率則隨流速的增加而減小[8-9]。季家東等采用流固耦合的順序求解法,研究了單排/多排彈性管束在均勻殼程流體或/和管程流體誘導下的振動響應,結果表明:彈性管束的振動主要由殼程流體誘導所致,兩不銹鋼連接體主要表現為面內振動,流速較低時存在明顯的2倍諧頻;均勻殼程流體誘導多排彈性管束振動時,迎流部分彈性管束的振動強度較大、頻率較高,背流部分彈性管束的振動強度較小、頻率較低,且各排彈性管束間的振動相互影響[10-12]。

本文以整體彈性管束換熱器為研究對象,利用通用CFD分析軟件CFX和ANSYS Workbench軟件的瞬態動力學分析模塊,采用流固耦合的順序求解法對不同管排間距和管排數條件下多排彈性管束的振動響應進行了數值研究。

1　數值計算方法

1.1　幾何模型

圖1所示為彈性管束換熱器及其殼程流體域示意圖,其中:換熱器筒體尺寸為Φ325 mm×10 mm;管程流體導入和導出管的尺寸為Φ45 mm×3 mm;殼程流體導入管尺寸為Φ60 mm×3 mm;殼程流體導出管尺寸為Φ73 mm×4 mm。

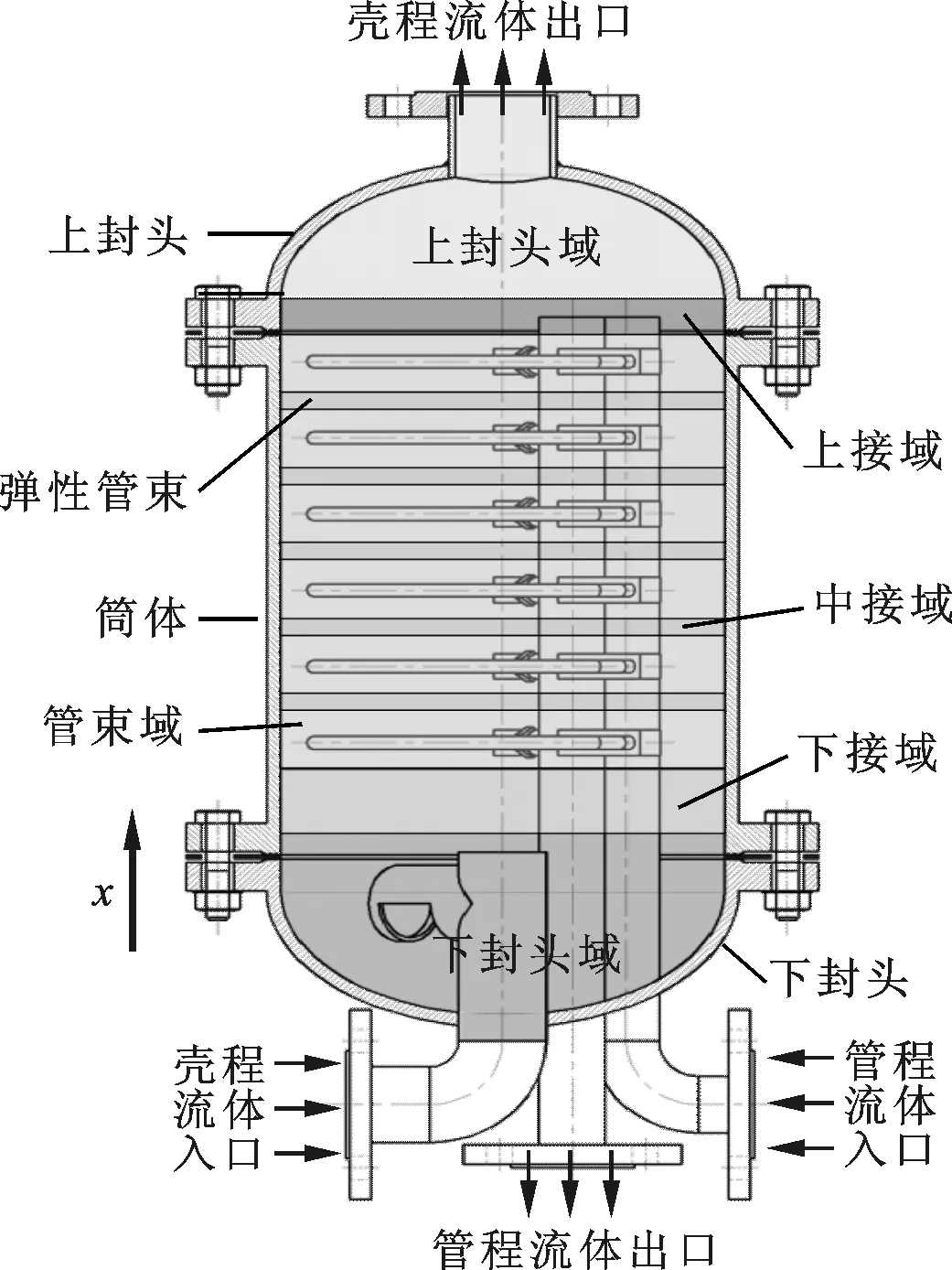
圖1　彈性管束換熱器及其殼程流體域示意圖

除彈性管束外,換熱器的其余各部分均由優質普通鋼制成。管程流體導入、導出管和殼程流體導入管均焊接在下封頭上,殼程流體導出管焊接在上封頭上,其余各部分間均由螺栓連接。

圖2所示為由4根紫銅彎管(半徑分別為R1、R2、R3、R4,外徑為d,壁厚為δ)和2個不銹鋼連接體(Ⅲ、Ⅳ)組成的彈性管束的幾何結構示意圖,各排彈性管束通過Ⅰ、Ⅱ兩端均勻固定在殼程流體導入、導出管上,管排間距為H,管排數為n。

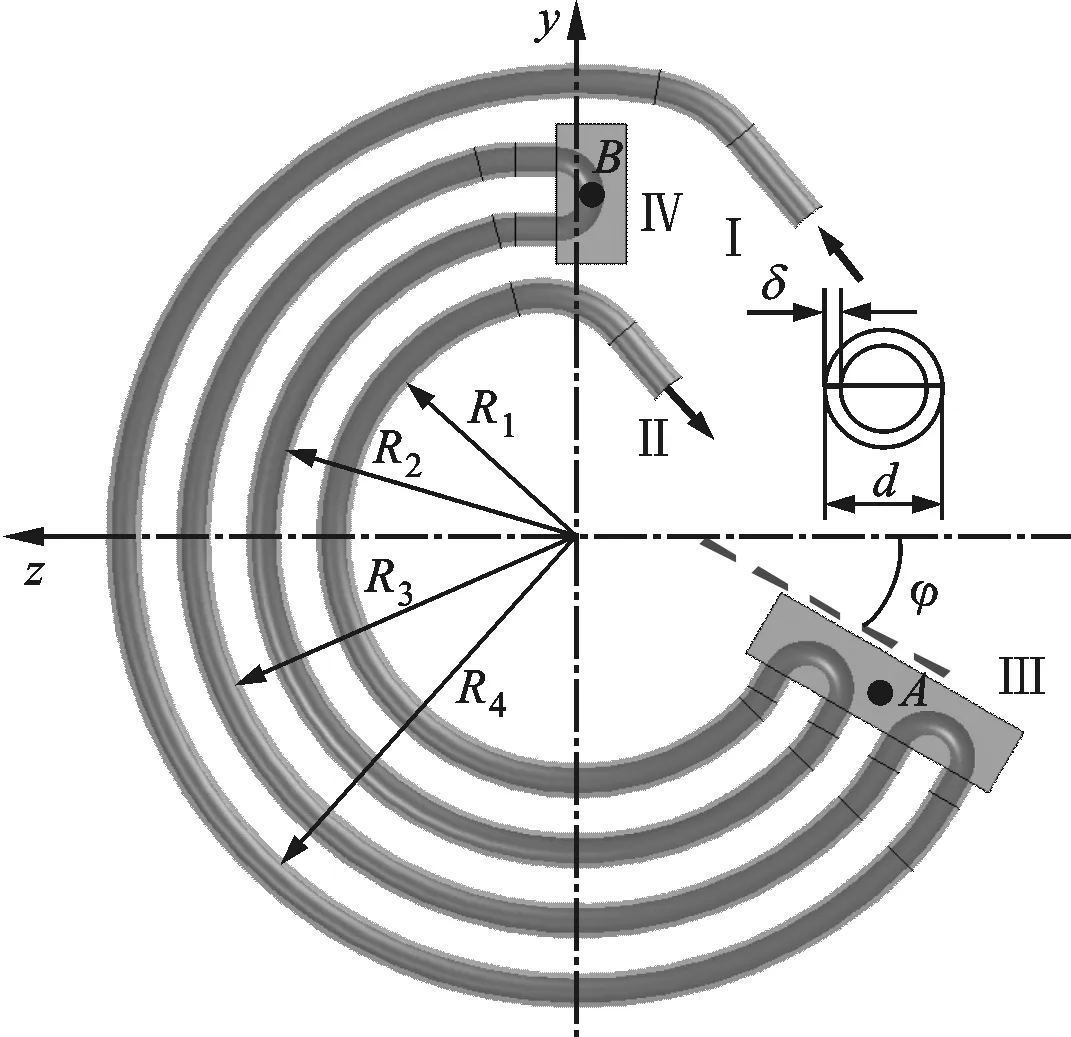
圖2　彈性管束結構示意圖

計算過程中,取彎管半徑R1=70 mm,R2=90 mm,R3=110 mm,R4=130 mm;連接體Ⅲ和Ⅳ的尺寸分別為80 mm×20 mm×20 mm和40 mm×20 mm×20 mm;管束外徑d=10 mm;管束壁厚δ=1.5 mm;夾角φ=45°;管排間距H=40,50,60,70 mm;管排數n=6,12。

為便于分析,換熱器內的彈性管束由下至上依次編號為1,2,…。為了監測各排彈性管束在殼程流場誘導下的振動響應,在每排彈性管束2個不銹鋼連接體上分別設置監測點Ai、Bi(i=1,2,…)。

1.2　網格劃分

因換熱器內各排彈性管束由彈性材料制成,在流體的誘導下較易產生振動,而換熱器外殼,殼程流體導入管和管程流體導入、導出管均為鋼結構,在流體誘導下基本不產生振動。為提高計算效率,在不影響計算結果的前提下,結構域部分僅保留各排彈性管束。

單排彈性管束的網格劃分策略如圖3所示,圖中A、B兩點是設立的監測點。從圖3可以看到,每排彈性管束網格由四面體網格(不銹鋼連接體)和六面體網格(紫銅彎管)組成,共9 366個單元、54 777個節點,最低網格質量為0.42。

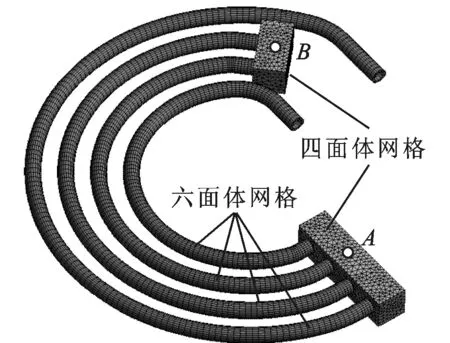
圖3　單排彈性管束網格劃分策略

為便于進行網格劃分,將殼程流體域分割為如圖1所示的6個部分,各部分的網格分割域如圖4所示。僅下封頭域采用四面體網格,其余各分割域均采用六面體網格。為提高計算精度,管束周圍流體域采用大密度網格,并布置6層邊界層網格。

(a)上封頭域　　　(b)下封頭域　　　(c)管束域

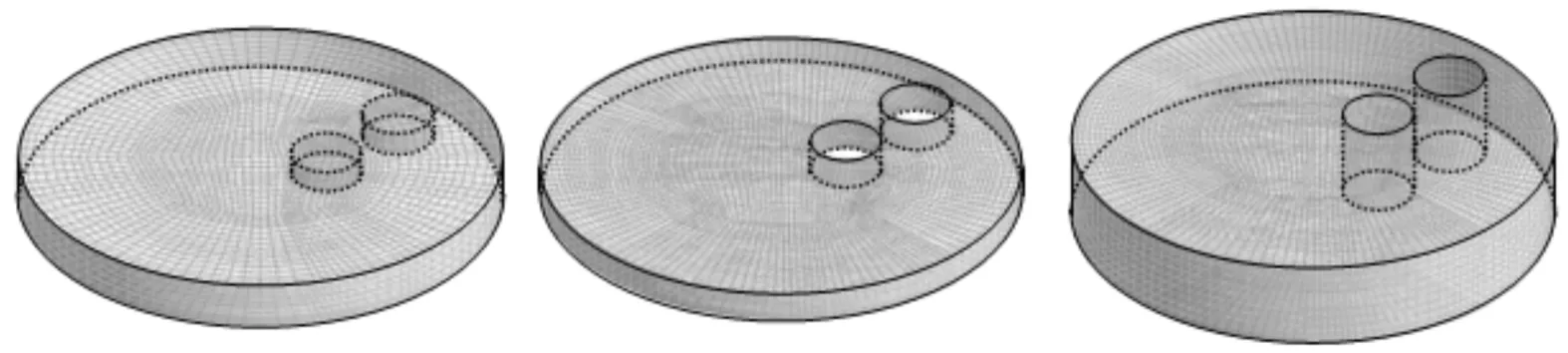
(d)上接域　　　　(e)中接域　　　　(f)下接域圖4　彈性管束網格分割域

表1所示為各分割域的網格數量和質量,可知最低網格質量為0.36,出現在上封頭域,為非流固耦合(FSI)計算區域,對計算結果基本無影響。

整體殼程流體域網格在CFX軟件中通過復制、平移和連接形成,各分割域間的網格連接均采用通用網格界面(GGI)的方式。

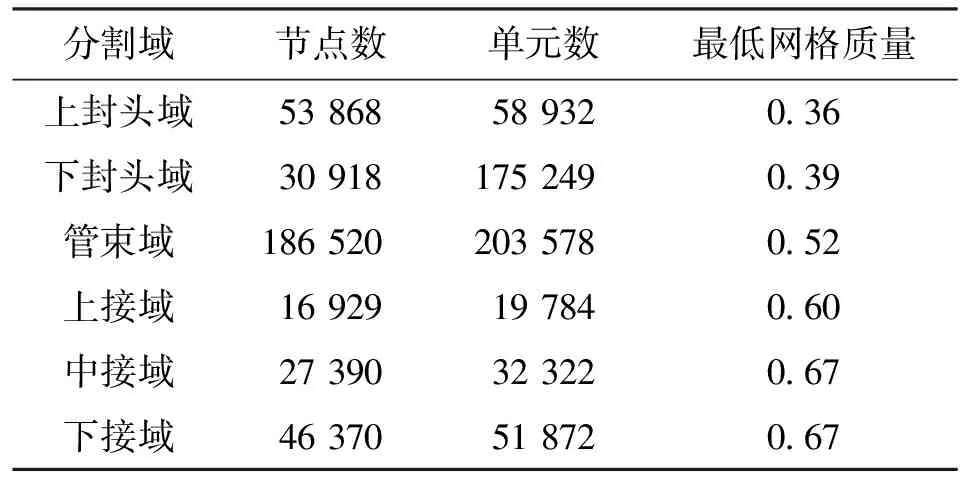
表1　各分割域的網格數量和質量

這樣,以管排間距H=60 mm的六排彈性管束換熱器為例,殼程流體域總單元數

ne=58 932+175 249+203 578×6+

19 784+32 322×5+51 872=1 688 915

(1)

殼程流體域總節點數

nd=53 868+30 918+186 520×6+

16 929+27 390×5+46 370=1 404 155

(2)

這種流體域分割的網格劃分策略,大幅提高了網格劃分的精度、效率和靈活性。通過改變中接域的高度,可組裝成不同管排間距的殼程流體域;通過改變管束域和中接域的復制數量,可組裝成任意管排數的殼程流體域。

1.3　數值分析方法

基于本文的研究問題,將求解域分成殼程流體域和結構域,流-固耦合(FSI)求解采用順序求解法在每個時間步長內獨立進行,通過建立FSI交界面實現流體域和結構域間的數據傳遞。

殼程流體域采用CFX軟件進行計算,流體介質為水,入口流速v為0.2 m/s或0.4 m/s(Re>2 300),屬湍流流動,選用標準k-ε模型進行計算。邊界條件設置:入口邊界類型為Inlet,給定入口速度0.4 m/s;出口邊界類型為Outlet,設置出口相對靜壓為0 Pa,計算環境設置為標準大氣壓(101.325 kPa);流體域內部與管束接觸面設置為FSI交界面。

結構域采用ANSYS Workbench軟件的瞬態動力學分析模塊進行計算。邊界條件設置:2個固定端I、II處截面為固定約束;各排彈性管束的外表面為FSI交界面,與流體域FSI交界面相對應;重力加速度為-x方向,取值為9.806 6 m/s2。

圖5所示為雙向FSI計算的基本流程,具體實施過程如下。

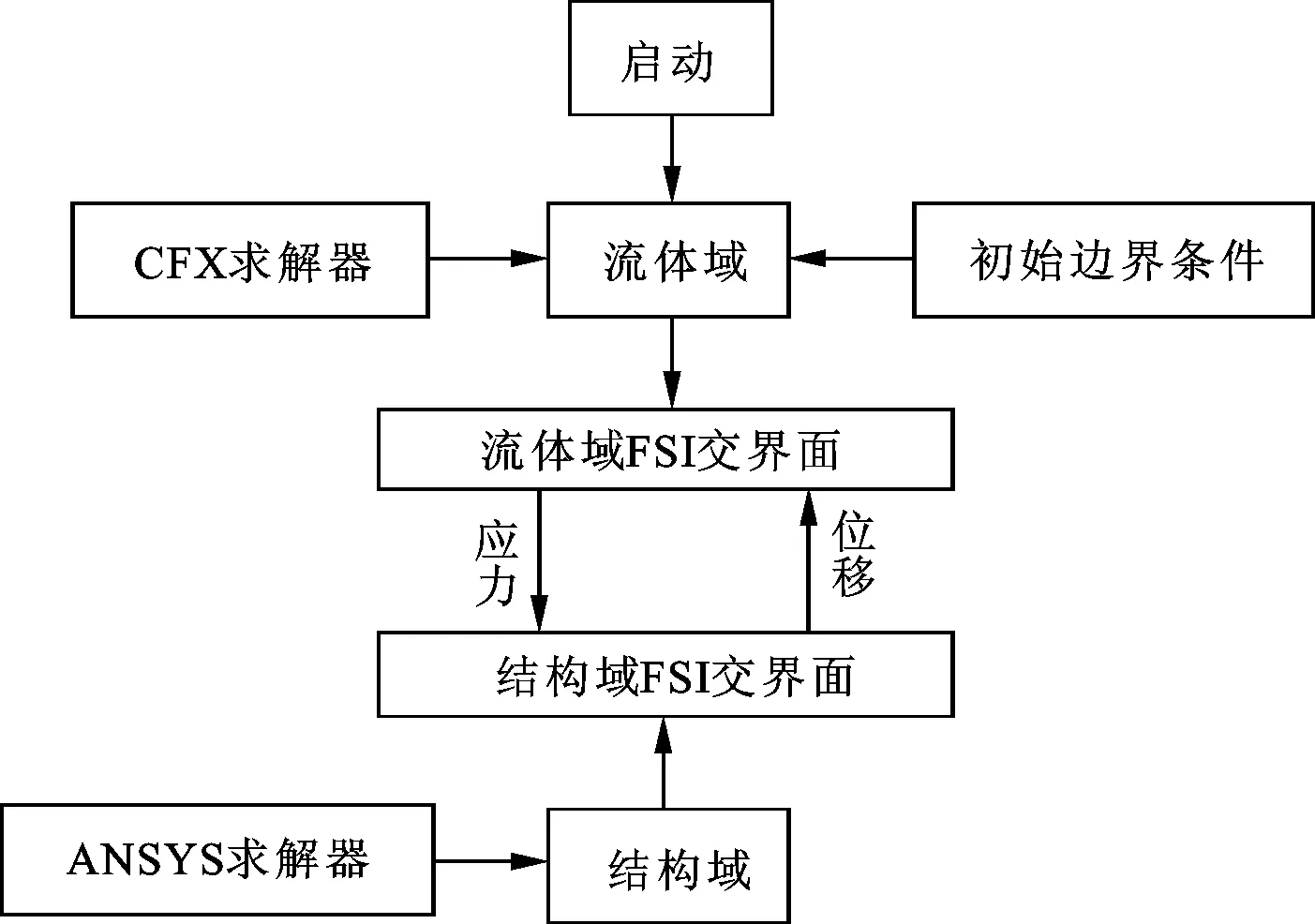
圖5　雙向FSI計算的基本流程

(1)基于初始邊界條件,采用CFX求解器進行流體域計算,得到流體域FSI交界面的應力。

(2)將求解的應力傳遞到結構域FSI交界面,以此為初始條件采用ANSYS求解器對結構域進行瞬態動力學計算,得到結構域FSI交界面的位移。

(3)將求解的位移反向傳遞到流體域FSI交界面,基于新的邊界條件進行下一個時間步長內流體域的計算。

(4)交替迭代,直至完成。

因網格較多,且FSI計算耗時,為得到殼程流場充分發展條件下彈性管束的振動響應,計算采用可大幅提高計算效率的粗算加精算的分步計算策略,具體步驟如下。

第1步:粗算,采用CFX軟件對殼程流體域進行計算,直到內部流場獲得充分發展。

第2步:精算,以粗算結果為初始條件進行FSI計算,直至監測點振動達到穩定,此時的振動響應即為殼程流場充分發展條件下彈性管束的振動響應。

1.4　結果驗證

為進行網格獨立性分析,基于3種不同的網格劃分方案,對v=0.4 m/s時六管束換熱器最底排彈性管束監測點在x方向的振動幅值Ax和頻率fx進行了計算,結果如表2所示。

表2　網格獨立性分析計算結果

ε:相對誤差,以方案2的計算結果為基準;t:計算時間。

表2中,節點數為整個求解域的總節點數,方案2為上面提到的網格劃分策略。兼顧計算精度和計算效率,選擇方案2的網格作為計算用網格滿足獨立性要求。

為驗證數值計算方法的正確性和準確性,利用文獻[2]中實驗用彈性管束的結構參數,建立與之相應的單排管束計算模型,對不同入口流速時2個監測點x方向的振動頻率fx和加速度ax進行了計算,數值計算結果與實驗測試結果的對比如表3所示。

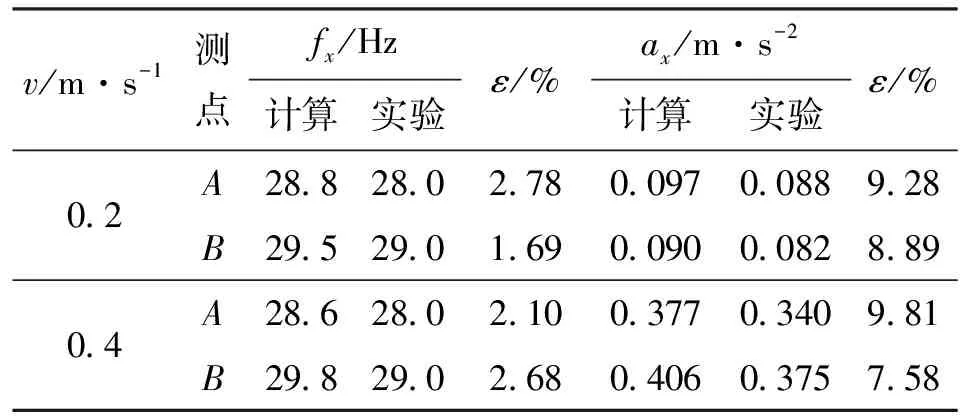
表3　數值計算結果與實驗測試結果的對比

由表3可知,數值計算結果與實驗測試結果基本一致,雖然加速度的相對誤差較大,但并未超過10%,由此驗證了數值計算方法的正確性和準確性。

2　結果與討論

2.1　振動響應分析

圖6所示為監測點A1在x方向的位移(Sx)隨FSI計算時間(tc)的變化。計算中如無特別說明,流體介質為水,v=0.4 m/s,H=60 mm,n=6。

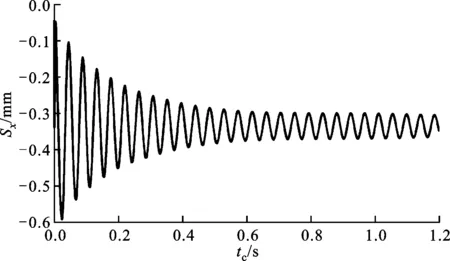
圖6　位移隨FSI計算時間的變化

從圖6可以看到,隨著FSI計算時間的增加,振動幅值逐漸減小并趨于穩定,當FSI計算時間tc=0.6 s時振動基本達到穩定,此時的振動響應即為殼程流場充分發展條件下監測點的振動響應。

表4所示為最底排(編號為1)和最頂排(編號為6)彈性管束監測點在不同方向的振動幅值和頻率,從中可以看到:

(1)連接體Ⅲ上監測點的振幅較大、頻率較低,連接體Ⅳ上監測點的振幅較小、頻率較高,各排彈性管束同一連接體上的監測點在各方向的振動頻率均一致,但幅值不同,這是因為在換熱器內部結構的影響下,連接體Ⅲ所在區域流體的流動速度較高所致;

(2)各監測點的振動均以x方向的振動為主,說明彈性管束的振動主要表現為面外振動,這是因為流經彈性管束的流體速度沿x方向的分量較小,振動主要體現為縱向流誘振,使得沿彈性管束平面方向的振動幅值較大。

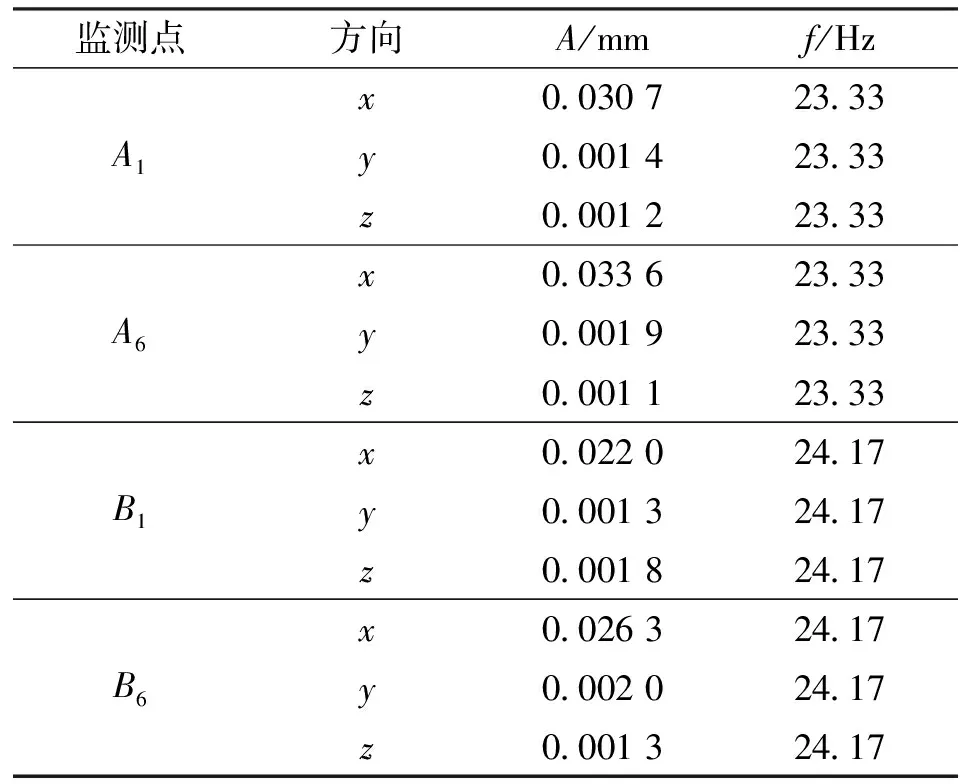
表4　監測點各方向的振幅和頻率

表5所列為不同入口流速條件下,各排彈性管束上的2個監測點在x方向的振幅Ax隨管束編號的變化數據,分析可知:

(1)各排彈性管束在相同監測點的最大相對誤差均較大,說明各排彈性管束的振動不均勻,隨著管束編號的增加,監測點振幅呈先增大后減小的趨勢,這是因為流體繞流前幾排管束后,生成了具有一定強度的脈動流,使得監測點的振幅逐漸增大,而隨著繞流管排數的增加,流體流動的紊流性和不規則性逐漸增強,從而導致監測點的振動強度逐漸降低;

(2)各排彈性管束連接體Ⅲ的振幅均大于連接體Ⅳ的振幅,說明連接體Ⅲ的振動較劇烈,如前面所述,造成這種現象的原因是流經連接體Ⅲ所在區域的流體具有較高的流動速度。

表5　監測點振幅隨管束編號的變化

注:帶圓圈數字為管束編號。

綜上所述,換熱器內各排彈性管束存在振動不均的現象,這是影響彈性管束換熱器使用壽命和傳熱效率的主要因素之一。結合高效彈性管束換熱器的設計準則,這一結論可為進一步實現振動的合理激發和有效控制提供依據。

2.2　管排間距對振動響應的影響

通過改變中接域的高度,并利用CFX軟件的網格復制、平移和連接功能,可組裝成不同管排間距的殼程流體域。

表6所列為不同管排間距(H=40～70 mm)條件下,最底排(編號為1)和最頂排(編號為6)彈性管束2個監測點在x方向的振幅和頻率。由表6可知:

(1)隨著H的增加,各監測點的頻率小幅降低,幅值基本呈先增大后減小的趨勢,這是因為流體繞流多排彈性管束時,間距比H/d(管排間距與管束外徑之比)存在一臨界值,當H/d等于臨界值時,管束振動強度最高,當H/d高于或低于這一臨界值時振動強度都會降低。

(2)對振幅而言,監測點Ai振幅的最大變化幅度(A1處為34.78%,A6處為48.54%)高于監測點Bi振幅的最大變化幅度(B1處為29.41%,B6處為39.89%),而對頻率而言,監測點Ai的頻率降幅(0.21%)低于監測點Bi的頻率降幅(1.87%),因此連接體Ⅲ上監測點的振幅受H的影響較大,連接體Ⅳ上監測點的頻率受H的影響較大。

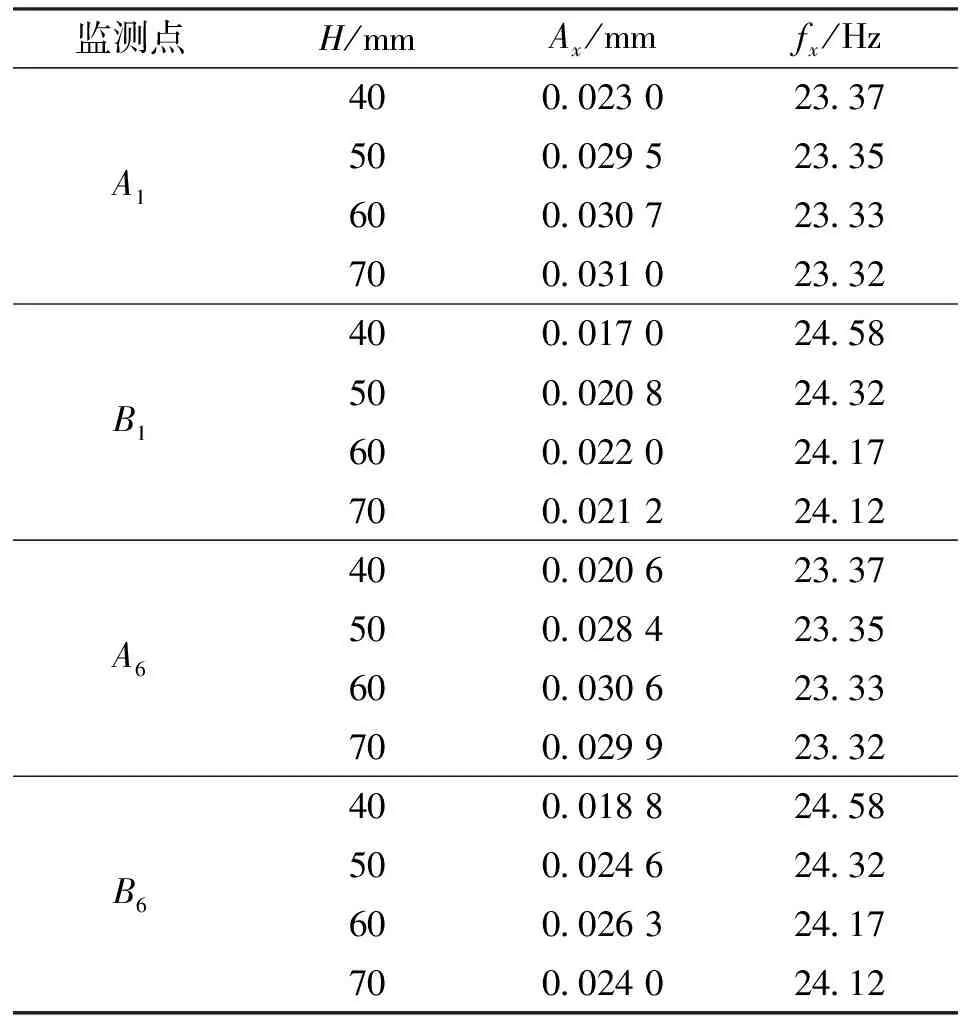
表6　不同管排間距時監測點x方向的振幅和頻率

圖7所示為不同管排間距(H=40,70 mm)時,各排彈性管束上的監測點在x方向的振幅隨管束編號的變化。

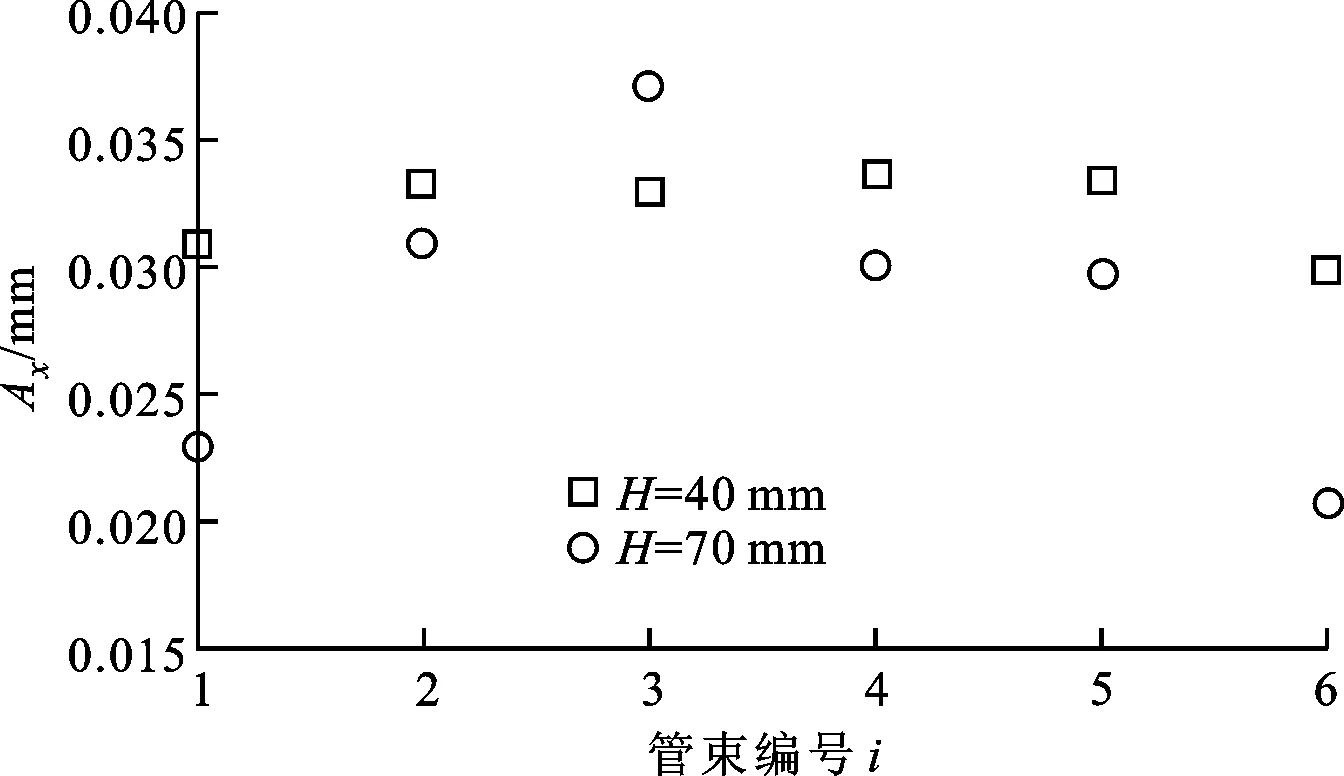
(a)不銹鋼連接體Ⅲ

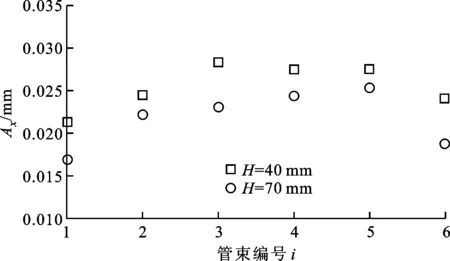
(b)不銹鋼連接體Ⅳ圖7　不同管排間距時監測點振幅隨管束編號的變化

從圖7可以看到:

(1)對連接體Ⅲ而言,監測點振幅在H=40 mm時的最大相對誤差為44.47%,在H=70 mm時的最大相對誤差為11.28%,而對連接體Ⅳ而言,監測點振幅在H=40 mm時的最大相對誤差為32.81%,在H=70 mm時的最大相對誤差為25.09%,這是因為當H較小時,各排管束間的相互影響較強,使得振幅隨管束編號的變化較劇烈;

(2)在H取不同值時,2個監測點的振幅隨管束編號的遞增基本呈先增大后減小的趨勢,當H較小(40 mm)時連接體Ⅲ振動的均勻性較差,當H較大(70 mm)時連接體Ⅳ振動的均勻性較差,這是由于流體域高度改變造成連接體附近流場改變引起的。

綜上所述,管排間距越小,各排管束間的相互影響就越強,管束振動的均勻性越差。在進行彈性管束換熱器的設計時,應綜合考慮換熱器的傳熱特性、阻力性能和使用壽命,選擇合適的管排間距。

2.3　管排數對振動響應的影響

通過改變管束域和中接域的復制數量,利用CFX軟件的網格復制、平移和連接功能,可組裝成管排數n為12的殼程流體域。表7所列為部分彈性管束2個連接體x方向的振幅和頻率。

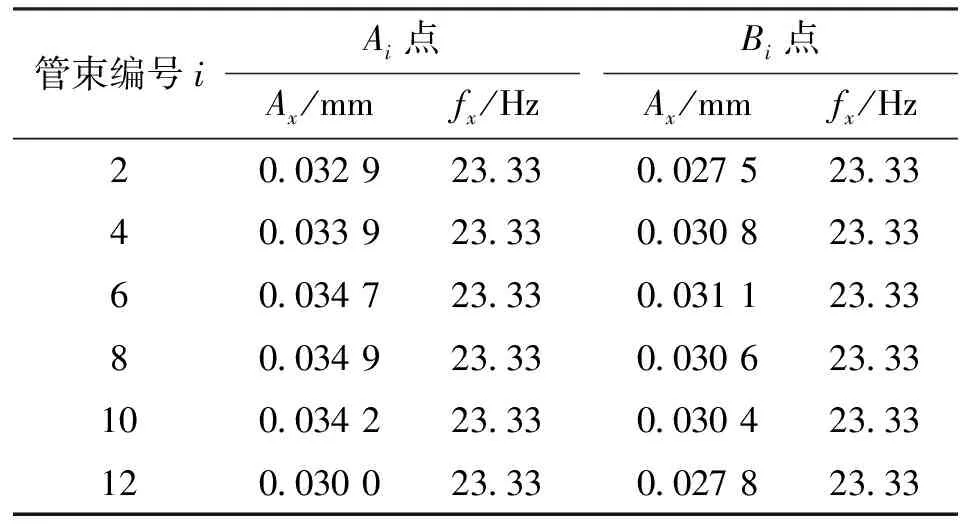
表7　部分監測點x方向的振幅和頻率

從表7可以看到:

(1)各排彈性管束同一連接體上監測點的振動頻率一致,且連接體Ⅳ上監測點的振動頻率較高;

(2)各排彈性管束同一連接體上監測點的振幅隨管束編號的增加呈先增大后減小的趨勢,且連接體Ⅲ上監測點的振幅較大。

圖8所示為管排數n=6,12時,各排彈性管束上監測點在x方向的振幅變化情況,從中可以看到:

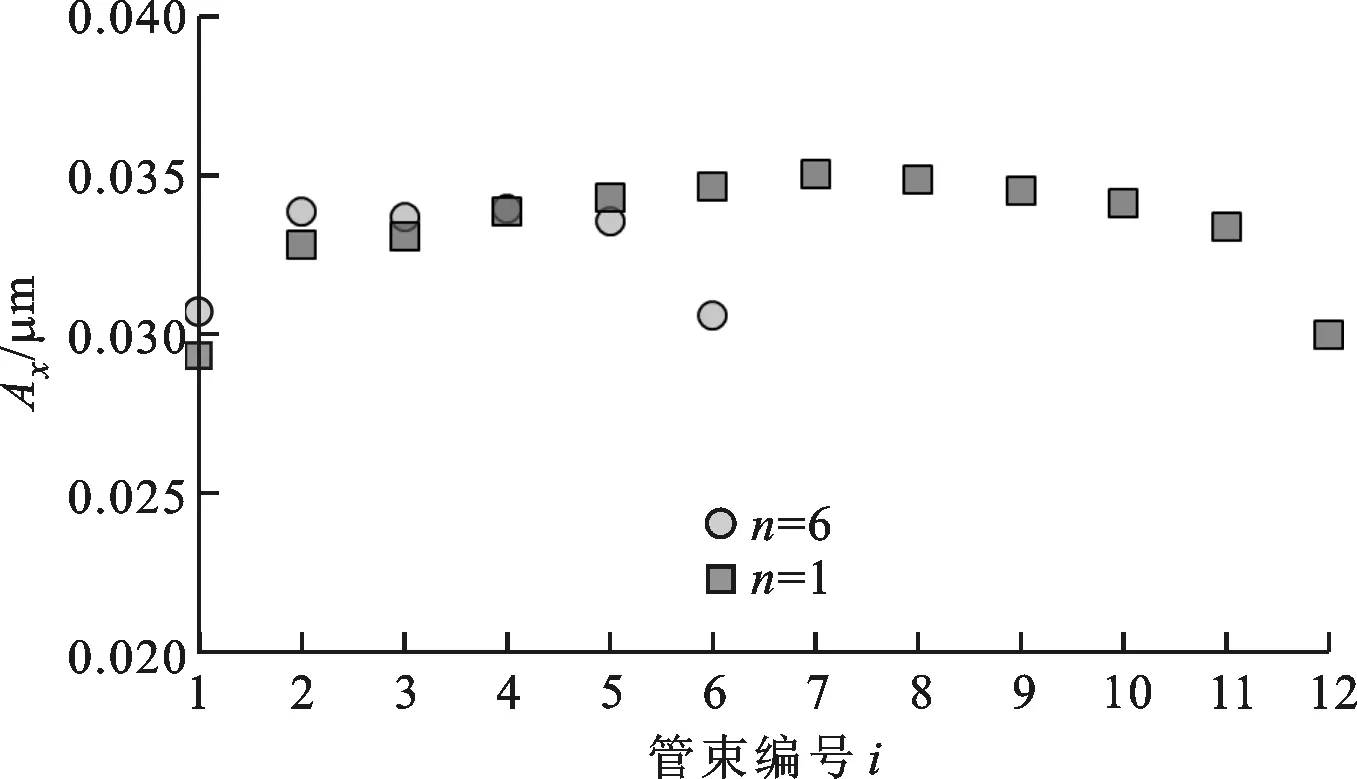
(a)不銹鋼連接體Ⅲ

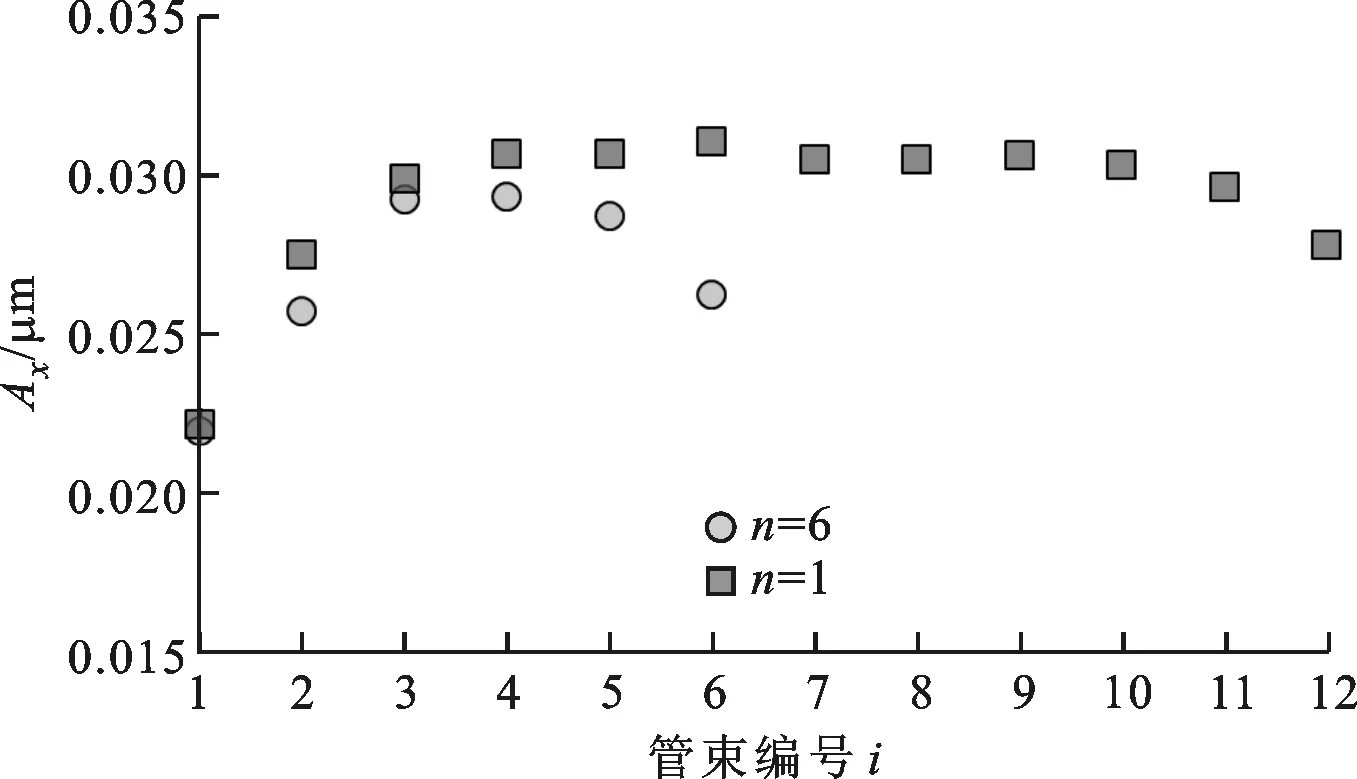
(b)不銹鋼連接體Ⅳ圖8　不同管排數時監測點振幅隨管束編號的變化

(1)各排彈性管束同位置監測點的振幅隨管束編號的增加先增大后減小,且這種變化趨勢不受管排數的影響;

(2)與連接體Ⅳ上監測點的振幅相比,連接體Ⅲ上監測點的振幅較大,亦不受管排數的影響;

(3)對于n=12時各監測點振幅的最大相對誤差來說,連接體Ⅲ的為16.53%,大于n=6時的10.00%,連接體Ⅳ的為28.70%,大于n=6時的25.17%,這說明隨管排數增加,各排管束的振動不均勻性增強,因為管排數增加時殼程流體域的高度也增加,進而影響換熱器內的流場分布。

綜上所述,在本文的計算參數范圍內,管排數不會影響內部管束振動的基本變化趨勢。對于更多管排數對換熱器傳熱特性的影響,還有待進一步探討。

3　結　論

本文以整體彈性管束換熱器為研究對象,基于流固耦合的順序求解法,對不同管排間距和管排數條件下多排彈性管束的振動響應進行了數值研究,并通過與實驗數據的對比,驗證了數值求解方法的正確性和準確性。獲得的主要結論如下。

(1)本文提出的粗算加精算的分步計算策略,可大幅減少計算時間,提高計算效率。

(2)在殼程流體誘導下,各監測點的振動主要表現為面外振動,且連接體Ⅲ(大連接體)的振動較劇烈;各排彈性管束的振動不均勻,監測點振幅隨著管束編號的增加呈先增大后減小的趨勢。

(3)當管排間距較小時,振幅隨管束編號的變化較劇烈,各排管束間的相互影響較大;隨著管排間距的增加,各監測點的頻率小幅降低,振幅基本呈先增大后減小趨勢;連接體Ⅲ上監測點的振幅受管排間距的影響較大,連接體Ⅳ(小連接體)上監測點的頻率受管排間距的影響較大。

(4)各排彈性管束同位置監測點的振幅隨管束編號的增加先增大后減小,連接體Ⅲ上監測點的振幅高于連接體Ⅳ上監測點的振幅,且這些變化規律不受管排數的影響;隨管排數量增加,各排管束的振動不均勻性增強。

參考文獻:

[1]CHENG Lin, LUAN Ting, DU Wenjing, et al. Heat transfer enhancement by flow-induced vibration in heat exchangers [J]. International Journal of Heat and Mass Transfer, 2009, 52(3): 1053-1057.

[2]宿艷彩. 彈性管束流體誘導振動及換熱特性研究 [D]. 濟南: 山東大學, 2012.

[3]YAN Ke, GE Peiqi, HONG Jun. Experimental study of shell side flow-induced vibration of conical spiral tube bundle [J]. Journal of Hydrodynamics, 2013, 25(5): 695-701.

[4]JI Jiadong, GE Peiqi, BI Wenbo. Numerical investigation on the flow and heat transfer performances of horizontal spiral-coil pipes [J]. Journal of Hydrodynamics, 2016, 28(4): 576-584.

[5]DUAN Derong, GE Peiqi, BI Wenbo, et al. Numerical investigation on the heat transfer enhancement mechanism of planar elastic tube bundle by flow-induced vibration [J]. International Journal of Thermal Sciences, 2017, 112: 450-459.

[6]JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on shell-side flow-induced vibration and heat transfer characteristics of elastic tube bundle in heat exchanger [J]. Applied Thermal Engineering, 2016, 107: 544-551.

[7]季家東. 彈性管束換熱器殼程分布式脈動流誘導管束振動研究 [D]. 濟南: 山東大學, 2016: 16-18.

[8]閆柯, 葛夢然, 高軍, 等. 空間錐螺旋管束流體誘導振動換熱器及性能分析 [J]. 西安交通大學學報, 2011, 45(11): 22-26.

YAN Ke, GE Mengran, GAO Jun, et al. Performance of flow-induced vibration heat exchanger with conical spiral tube bundle [J]. Journal of Xi’an Jiaotong University, 2011, 45(11): 22-26.

[9]YAN Ke, GE Peiqi, HU Ruirong, et al. Heat transfer and resistance characteristics of conical spiral tube bundle based on field synergy principle [J]. Chinese Journal of Mechanical Engineering, 2012, 25(2): 370-376.

[10] 季家東, 葛培琪, 畢文波. 流體誘導彈性管束振動響應數值分析 [J]. 振動與沖擊, 2016, 35(6): 80-84.

JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on flow-induced vibration responses of elastic tube bundle [J]. Journal of Vibration and Shock, 2016, 35(6): 80-84.

[11] 季家東, 葛培琪, 畢文波. 換熱器內彈性管束流體組合誘導振動響應的數值分析 [J]. 西安交通大學學報, 2015, 49(9): 24-29.

JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on combination flow induced vibration responses of elastic tube bundle in heat exchanger [J]. Journal of Xi’an Jiaotong University, 2015, 49(9): 24-29.

[12] 季家東, 葛培琪, 畢文波. 換熱器內多排彈性管束殼程流體誘導振動響應的數值分析 [J]. 振動與沖擊, 2016, 35(20): 85-89.

JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on shell-side flow induced vibration responses of multi-row elastic tube bundles in heat exchanger [J]. Journal of Vibration and Shock, 2016, 35(20): 85-89.