采用俞茂宏統一強度理論求解圓筒和球殼的極限值

田紅亮, 彭文昱, 何孔德, 董元發, 杜義賢, 鐘先友, 王驍鵬, 郤能

(三峽大學機械與動力學院, 443002, 湖北宜昌)

以教材和工程中的4種常用強度理論和莫爾強度理論為例,每種強度理論的發展和完善都經過了幾十年以至上百年的時間:第一強度理論從1638年伽利略關于梁的彎曲實驗到1858年郎肯進行全面闡述;第二強度理論從1682年Mariotte的伸長斷裂概念、Poncelet的最大應變假設到1856年圣維南建議以最大應變作為材料極限強度的設計依據;第三強度理論從1773年庫侖、1864年特雷斯卡到1900年Guest的最大剪應力強度理論;第四強度理論從1904年Huber的歪形能準則、1913年馮米澤斯的屈服圓方程到1937年納達依的八面體剪應力理論;莫爾強度理論從1773年庫侖到1900年莫爾的單剪強度理論。西安交通大學的俞茂宏教授從1961年提出雙剪應力屈服準則以后,根據一點應力狀態的3個主剪應力中只有2個獨立量,并考慮到2個較大主剪應力作用面上的正應力,以及中間主應力效應的區間性,系統而全面地研究了強度理論,逐步發展形成了雙剪統一強度理論體系。雙剪統一強度理論的系列化準則不僅符合德魯克公式,并且涵蓋了從內邊界到外邊界的全部區域。雙剪統一強度理論是一個能夠實現全覆蓋的強度理論,簡稱為統一強度理論,德國學者首先將其稱為俞茂宏統一強度理論[1]。統一強度理論代表了該領域的一個重大貢獻。在國際上享有聲望的期刊上發表的綜述性論文,常是應編者邀請而寫,反映作者在有關領域內已經取得了系統性成果并在國際上享有一定的聲望與學術地位,因此對國外知名期刊發表的綜述性論文應該給以高于一般研究論文的評價。2002年,俞茂宏教授在著名力學期刊《Applied Mechanics Reviews》上獨撰發表了關于強度理論研究進展的論文,引用的參考文獻達1 163篇之多[2]。這篇論文已由北京工業大學彭一江教授翻譯成中文[3],于2004年發表于《力學進展》。俞茂宏教授的成就使中國學者在材料強度理論研究方面已占有一席之地,在人們熟知的特雷斯卡、馮米澤斯、莫爾、庫侖等外國人名之后,首次出現了中國人的名字——俞茂宏。

在工程實際中,圓筒和球殼具有非常廣泛的運用,如充壓氣瓶、傳動筒缸體、壓力容器和高壓管道等。近年來,圓筒演變成套管,球殼發展為球罐,已成為港口及深海工程中發展起來的一種新型結構,在我國沿海地區得到了大量運用。眾多學者已對圓筒和球殼的極限載荷進行了大量研究,例如:俞茂宏對薄壁壓力容器的強度與壁厚進行了設計,還給出了承受內部壓力厚壁圓筒的彈性極限壓力和塑性極限壓力的統一解[4];Lin等在充分考慮套管拉壓強度差、中間主應力、材料硬化、屈強比對套管全壁屈服擠毀壓力影響的基礎上,根據統一強度理論推導出均勻外壓下套管全壁屈服擠毀壓力的統一算法[5],此外,還給出了計算高抗擠套管擠毀強度的公式[6];Law等給出了預測高屈強比套管中爆炸壓強的23種方法以及預報失效應變的6種方法[7];Güven分析了不同極限強度對厚壁壓力容器塑性應變的影響[8];Sun等提出了僅承受外載荷時石油套管擠毀強度的計算公式[9],但公式中許多系數不精確,不能完全模擬套管擠毀的復雜機理;Xu等運用統一強度準則對承受內壓厚壁圓筒的安定性進行了分析[10];趙德文等為使馮米澤斯屈服準則線性化,在Haigh-Westergaard應力空間,將特雷斯卡屈服函數與雙剪應力屈服函數相加并取其平均屈服函數作為平均屈服準則,給出了平均屈服準則的數學表達式、屈服軌跡與單位體積塑性功率表達式,計算了當拉壓強度比α=1與中間主應力系數b=1/3時的廣義雙剪準則典型特例[11],還在π平面上取特雷斯卡屈服軌跡與雙剪應力屈服軌跡之間誤差三角形的幾何中線確定屈服軌跡,建立了Haigh-Westergaard應力空間的應力方程,計算了當α=1和b=0.4時的廣義雙剪準則的特例[12],并且將α=1和b=0.4時的廣義雙剪準則應用于內壓薄壁圓筒和球殼的塑性極限分析,獲得了極限載荷的解析解[13];翟越等采用俞茂宏統一強度理論,分析了高壓薄壁圓筒在三向應力狀態下的極限荷載,得出了統一解形式[14];Jin等基于統一強度準則對內壓作用下薄壁管道的塑性失效進行了分析,并考慮強度差異效應和強度準則對爆破壓力的影響,得到了兩端封閉薄壁長圓管道的爆破壓力解析解[15];李子豐討論了統一強度理論在桿管柱力學中的適用性,建立了具有強度差異效應材料的安全應力域[16]。

通過對上述研究內容的分析發現:①大多數文獻忽略了圓筒和球殼的徑向正應力σr,即認為σr=0,將三向應力狀態處理為二向應力狀態,不符合實際;②現有文獻或使用俞茂宏統一強度理論的第一式,或使用第二式,而事實上,俞茂宏統一強度理論有2個數學表達式,應用時必須分析單元體的應力狀態,嚴格論證適用于哪一個判別式。對于薄壁圓筒,應該會同時用到這2個數學表達式。

本文考慮了圓筒和球殼的徑向正應力σr,在求解薄壁圓筒的彈性極限壓強和最小壁厚時,按照俞茂宏統一強度理論,根據參數滿足的條件,同時采用第一式和第二式;在求解厚壁圓筒的縱向極限承載能力時,區分了鋼管的橫截面面積與核心混凝土的橫截面面積;求解了球殼的彈性極限壓強和最小壁厚;通過實例計算與分析,得到了各設計變量對極限參數的影響規律。

1　薄壁圓筒的彈性極限壓強

當鋼管的壁厚t遠小于它的內直徑d時,稱為薄壁圓筒。若封閉的薄壁圓筒所受內壓強為p,則徑向壓應力

σr=-p

(1)

在筒壁的縱向截面上環向正應力

(2)

圓筒橫截面上的軸向拉應力

(3)

最大主應力、中間主應力、最小主應力分別為

(4)

(5)

σ3=σr=-p

(6)

俞茂宏在1961年提出的雙剪屈服準則適用于拉壓強度相同的材料。雙剪屈服準則的2個數學表達式為

(7a)

(7b)

式中:σt為抗拉強度。

俞茂宏在1985年提出了廣義雙剪強度理論,該理論的2個數學表達式為

(8a)

(8b)

式中:α為拉壓強度比。

俞茂宏在1991年提出了主應力形式的統一強度理論。統一強度理論將復雜應力的常用變量從主應力轉換為主剪應力,并按照3個主剪應力中只有2個獨立量的規律,提出雙剪的思想,構造了2個雙剪正交八面體的單元體模型。最大主剪應力、2個中間主剪應力[17-18]分別為

(9)

(10)

(11)

作用在3個主剪應力面上的3個正應力為

(12)

(13)

(14)

統一強度理論的數學建模方程為

τ13+bτ12+β(σ13+bσ12)=C,

τ12+βσ12≥τ23+βσ23

(15a)

τ13+bτ23+β(σ13+bσ23)=C,

τ12+βσ12≤τ23+βσ23

(15b)

式中:b為中間主應力系數;β和C為材料常數,由試驗確定。

對于單向拉伸試驗,最大主應力、中間主應力、最小主應力依次為

σ1=σt;σ2=σ3=0

(16)

將式(9)、(10)、(12)、(13)和(16)代入式(15a),可得

(1+b)(1+β)σt=2C

(17)

對于單向壓縮試驗,最大主應力、中間主應力、最小主應力依次為

σ1=σ2=0;σ3=-σc

(18)

式中:σc為抗壓強度。

將式(9)、(11)、(12)、(14)和(18)代入式(15b),得

(1+b)(1-β)σc=2C

(19)

由式(17)與式(19)相等,得[19]

(20)

式中:α=σt/σc。將式(20)代入式(17),得

(21)

將式(9)～(14)和式(20)、(21)代入式(15a),得

(廣義拉伸應力狀態)

(22a)

將式(9)、(11)、(12)、(14)、(20)和(21)代入式(15b),得

(廣義壓縮應力狀態)

(22b)

在式(22a)和(22b)中,σ2為中間主應力,故b稱為中間主應力系數。

按照式(22a),現假設

(23)

將式(23)的第二式代入第一式消去σ1,可得中間主應力的臨界值

(24)

按照式(22b),亦可假設

(25)

將式(25)的第二式代入第一式消去σ1,也可得中間主應力的臨界值,結果與式(24)相同。

將式(22a)、(22b)和式(24)合寫成一個數學表達式,得

(26)

由式(24),可得Kolupaev綜合變量[20-21]

(27)

俞茂宏統一強度理論可以充分反映出中間主應力對材料屈服或破壞的影響[22],如圖1所示。從圖1a可見,圖中最上面的一條曲線(b=1)為雙剪理論的極限面,最下面的一條曲線(b=0)為單剪理論的極限面,俞茂宏統一強度理論覆蓋了從單剪到雙剪的全部區域。圖1b和1c皆表明:俞茂宏統一強度理論可得到分段線性的中間主應力σ2的效應,這種效應是非單調的;在分段直線的首末兩點,最大主應力近似相等。在圖1d中,第三強度理論對應一六角形曲線,第四強度理論對應一橢圓曲線。

(28)

成立,將式(4)～(6)代入式(28),得

(29)

將式(4)～(6)代入式(22a),得

(30)

由式(30),可得到薄壁圓筒的彈性極限壓強

(31)

為了確保圓筒在軸壓時不發生局部屈曲,壁厚不能太小。由式(30),可得到薄壁圓筒的最小壁厚

(32)

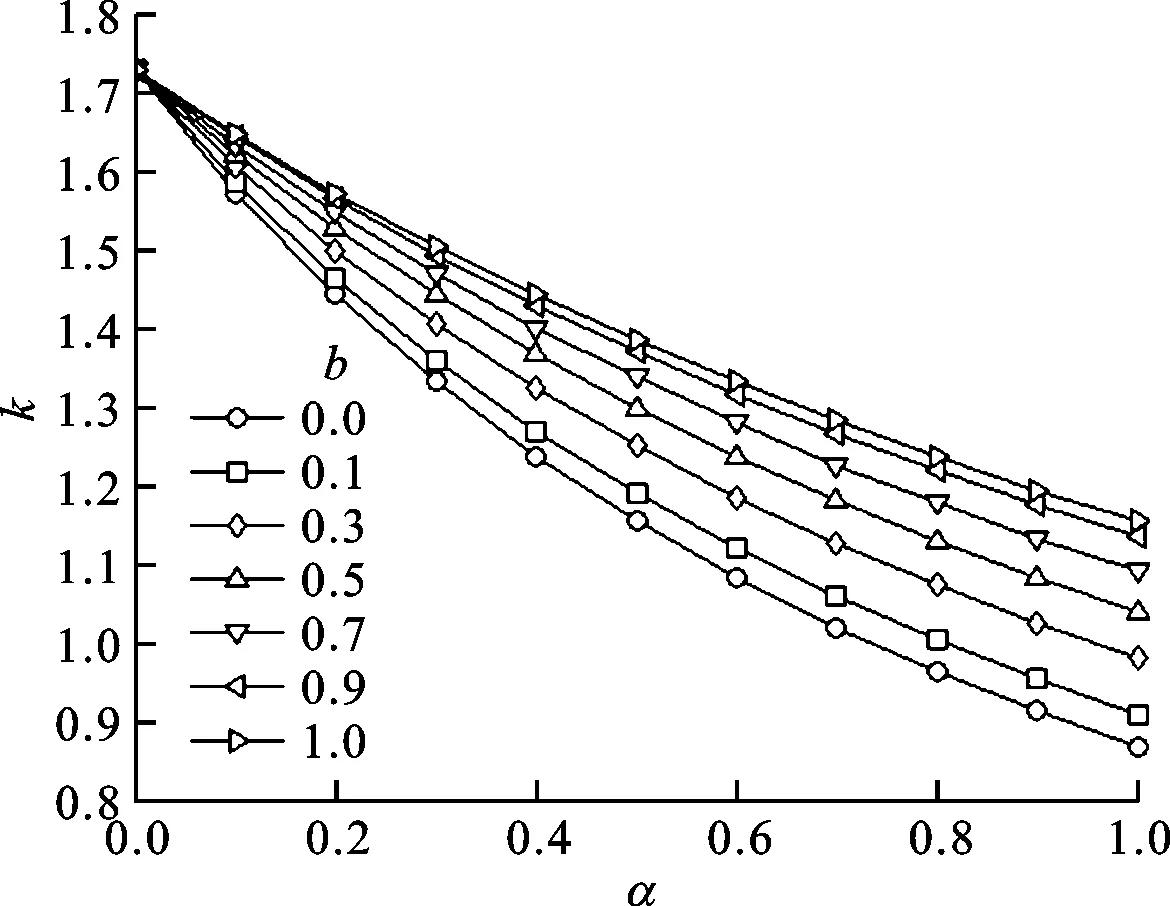
(a)Kolupaev綜合變量

(b)α=1和σ3/σt=0.2時的最大主應力

(c)α=1和b=1時的最大主應力

(d)第三強度理論與第四強度理論對應的曲線圖1　由俞茂宏統一強度理論獲得的曲線

(33)

成立,將式(4)～(6)代入式(33),得

(34)

將式(4)～(6)代入式(22b),得

(35)

由式(35),可得到薄壁圓筒的彈性極限壓強

(36)

由式(35),可得到薄壁圓筒的最小壁厚

(37)

2　厚壁圓筒的縱向極限承載能力

厚壁圓筒受內壓強p時,其塑性極限內壓強

(38)

式中:r為鋼管的內半徑;R為鋼管的外半徑。

塑性極限內壓強在鋼管上派生的縱向極限力

(39)

式中:π(R2-r2)為鋼管的橫截面面積;πr2為核心混凝土的橫截面面積。

將式(38)代入式(39),得

(40)

在核心混凝土上有接觸應力σ3,由于σ3的作用單元體將向周圍膨脹,于是引起周圍材料對它的約束應力σ2和σ1。鋼管混凝土軸心受壓構件中由于鋼管對混凝土的約束作用,使核心混凝土處于軸向壓縮和側向均勻圍壓的三向應力狀態[23],三軸受壓核心混凝土的縱軸向抗壓強度

R0=Ra+Kpp

(41)

式中:Ra為圓柱體混凝土在單軸受壓時的抗壓強度;K為側壓效應系數。

將式(38)代入式(41),得

R0=

(42)

縱軸向抗壓強度在核心混凝土上派生的縱向極限力

P0=πr2R0

(43)

將式(42)代入式(43),得

(44)

鋼管和混凝土組成圓筒,故厚壁圓筒的縱向極限承載力

P=Ps+P0

(45)

將式(40)和(44)代入式(45),得

P=

(46)

套箍混凝土是配有密排的螺旋式箍筋、焊接環形箍筋、橫向方格鋼筋網和鋼管等各種套箍的混凝土。各種形式的套箍對其所包圍的核心混凝土能起到側向約束的作用,使之處于三軸受壓的應力狀態而具有較高的抗壓強度和較大的極限壓縮變形,此即混凝土的套箍強化。套箍指標是影響鋼管混凝土短柱極限承載能力的重要綜合因素,套箍指標[24]為

(47)

由式(47)得

(48)

3　球殼的彈性極限壓強

若球殼所受內壓強為p,則徑向壓應力

σr=-p

(49)

用包含直徑的平面把球殼分成2個半球,包含直徑的任意截面上皆無切應力,且沿壁厚上的正應力都相等。最大主應力、中間主應力、最小主應力依次為

(50)

(51)

σ3=σr=-p

(52)

式(50)～(52)使以下不等式恒成立

(53)

將式(50)～(52)代入式(22b),得

(54)

由式(54),可得到球殼的彈性極限壓強

(55)

更值得一提的是,式(55)不包含中間主應力系數b,能夠消去b的原因在于,由式(50)和(51)得σ1=σ2,從而在式(22b)中約去了b。

由式(54),可得到球殼的最小壁厚

(56)

經典的第四強度理論的屈服準則為

(57)

將式(50)～(52)代入式(57),得

(58)

由式(58),可得到經典的第四強度理論的彈性極限壓強

(59)

由此可見,當α=1時,俞茂宏統一強度理論的式(55)退化成非線性第四強度理論的式(59)。

4　圓筒和球殼極限載荷的實例分析

4.1　薄壁圓筒彈性極限壓強的影響因素

對于一承受內壓p的薄壁壓力容器,鋼管內直徑d=2 000 mm,低碳鋼材料的抗拉強度σt=200 MPa,壁厚t=10 mm,取安全因數n=1.5[25],其彈性極限壓強的變化規律如圖2所示。

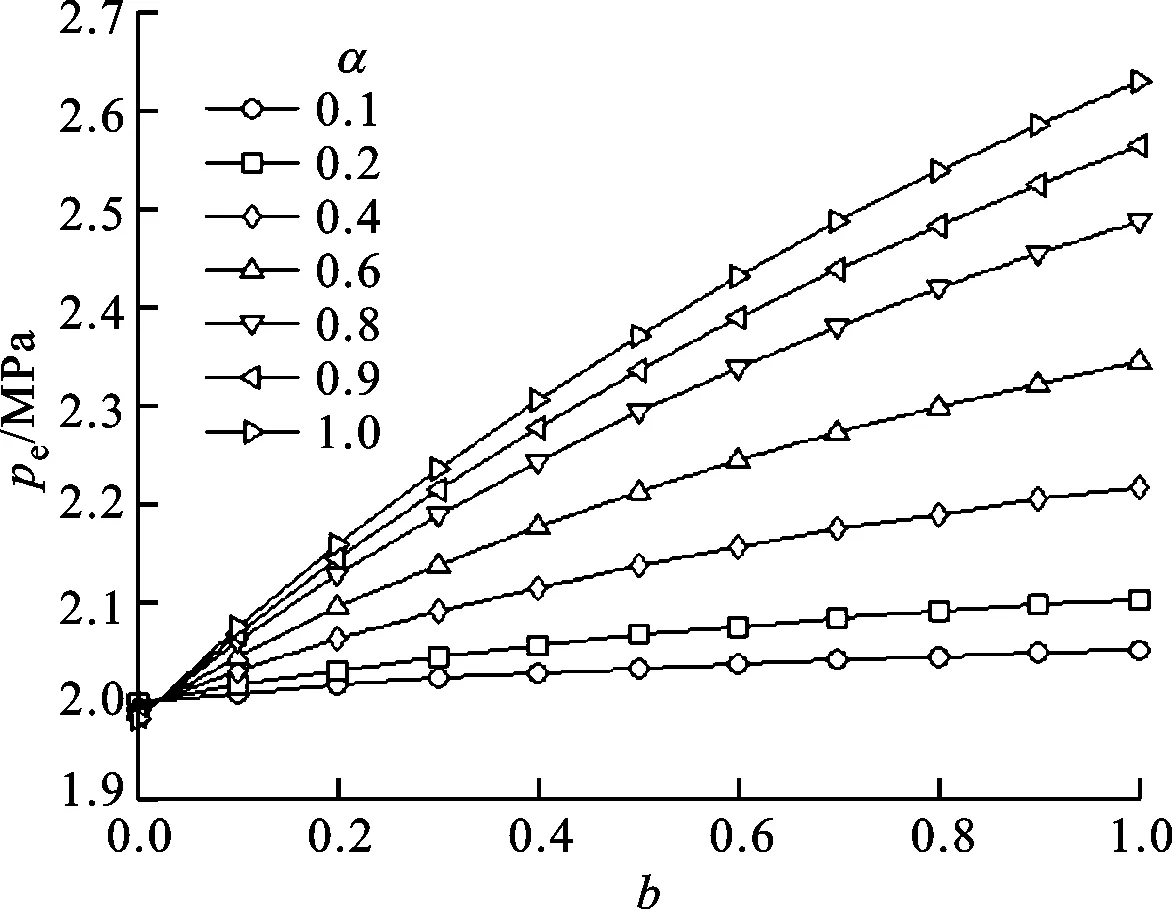
(a)彈性極限壓強與中間主應力系數b的關系

(b)彈性極限壓強與拉壓強度比α的關系

(c)本文方法與強度理論得到的彈性許用壓強圖2　薄壁圓筒彈性極限壓強的變化規律

在圖2a和2b中,當α≤50/51=0.980 4時,采用式(31);當α≥50/51=0.980 4時,采用式(36);當α=0.980 4時,2個公式計算的結果相同。由圖2a可以看出,薄壁圓筒的彈性極限壓強隨中間主應力系數的增大而增大。由圖2b可以看出:當中間主應力系數很小時,薄壁圓筒彈性極限壓強隨拉壓強度比的增大而略微減小;當中間主應力系數較大時,彈性極限壓強隨拉壓強度比的增大而增大。由圖2c可以看出,本文的彈性許用壓強小于文獻[4]的,說明本文的計算結果偏于安全。

4.2　薄壁圓筒最小壁厚的影響因素

對于一承受內壓p=1.6 MPa的薄壁壓力容器,鋼管內直徑d=2 000 mm,低碳鋼材料的抗拉強度σt=200 MPa,取安全因數n=1.5,其最小壁厚的變化規律如圖3所示。

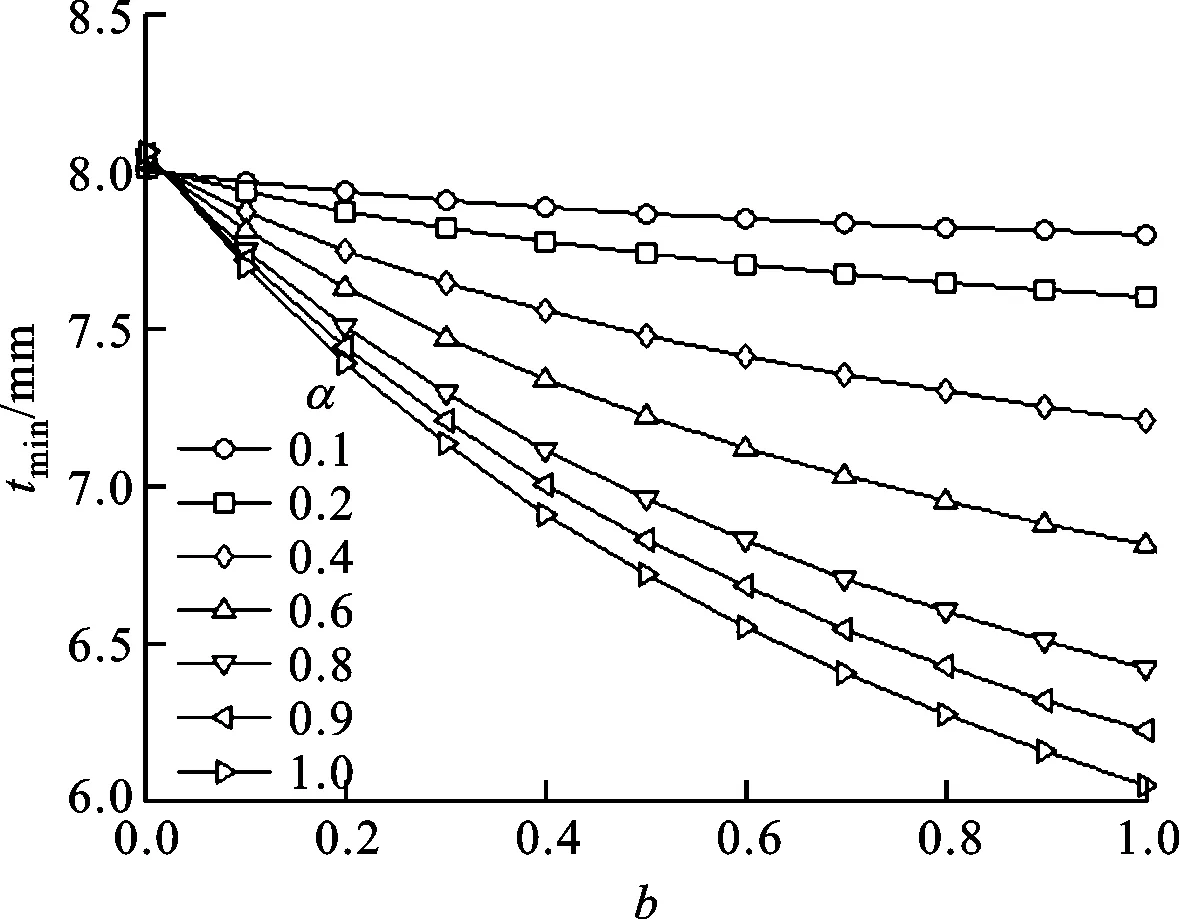
(a)最小壁厚與中間主應力系數b的關系

(b)最小壁厚與拉壓強度比α的關系

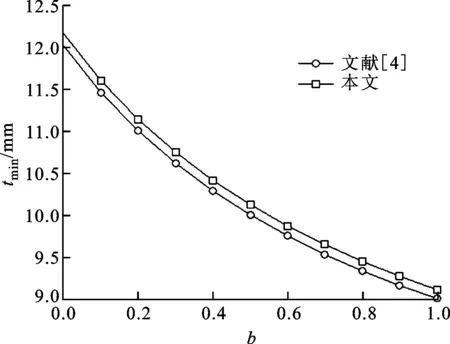
(c)本文方法與強度理論得到的許用最小壁厚圖3　薄壁圓筒最小壁厚的變化規律

由圖3a可以看出,薄壁圓筒最小壁厚隨中間主應力系數的增大而減小。由圖3b可以看出:當中間主應力系數很小時,薄壁圓筒最小壁厚隨拉壓強度比的增加僅有微小的增加;當中間主應力系數較大時,薄壁圓筒最小壁厚隨拉壓強度比的增大而減小。由圖3c可以看出,本文的許用最小壁厚大于文獻[4]的,說明本文的計算值偏于安全。

4.3　厚壁圓筒極限載荷的影響因素

保持理論研究與試驗研究的相對獨立性,使它們更客觀,這是國際上關于材料強度理論研究的一種共識[26]。取α=1和b=1/2時,本文計算的厚壁圓筒縱向極限承載力與試驗數據[27]的比較情況見表1,從中能夠看出,本文縱向極限承載力的計算值與試驗數據之間的相對誤差在-7.498 5%～7.106 0%的范圍內。

表1　縱向極限承載力的試驗值[27]、計算值及其誤差

Φt:套箍指標試驗值;Φd:套箍指標計算值;e:Φd與Φt之間的相對誤差;Pt:縱向極限承載能力試驗值(取平均值);Pd:縱向極限承載能力計算值;ω:Pd與Pt之間的相對誤差。

2、4號試件縱向極限承載力的變化規律分別如圖4、圖5所示。由圖4a和5a可知,縱向極限承載力隨中間主應力系數的增大而增大。由圖4b和5b可知:當中間主應力系數較小時,縱向極限承載力隨拉壓強度比的增大而減小;當中間主應力系數較大時,縱向極限承載力隨拉壓強度比的增大而增大。

由圖2a、3a、4a和5a可知,多條曲線相交于同一點(其橫坐標為b0),橫坐標均為中間主應力系數b,圖例中的變量皆為拉壓強度比α,表明在此同一交點的左右兩側(即bb0),縱坐標與拉壓強度比α之間的單調增減關系發生了突變。根據式(31)可得

從圖1a、2b、3b、4b和5b可以看出,多條曲線相交于同一點(其橫坐標為α=0),橫坐標均為拉壓強度比α,圖例中的變量皆為中間主應力系數b,即當α=0時,縱坐標不依賴于中間主應力系數b,見式(27)、(31)、(32)和(46)。

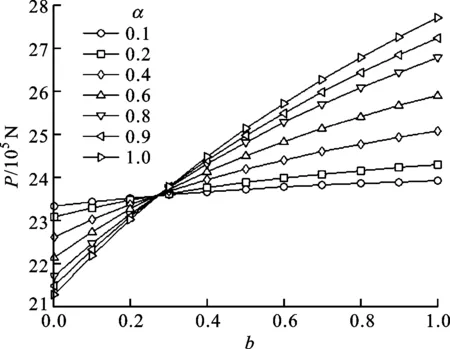
(a)縱向極限承載力隨中間主應力系數b的變化

(b)縱向極限承載力隨拉壓強度比α的變化圖4　厚壁圓筒2號試件縱向極限承載力的變化規律

(a)縱向極限承載力隨中間主應力系數b的變化

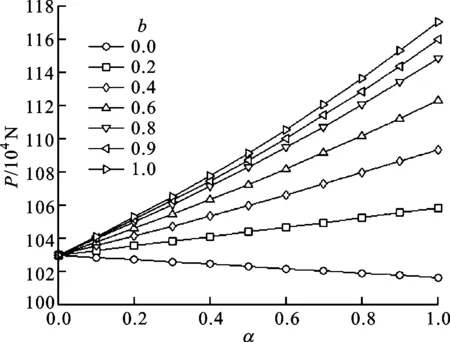
(b)縱向極限承載力隨拉壓強度比α的變化圖5　厚壁圓筒4號試件縱向極限承載力的變化規律

為研究徑厚比的增大對塑性極限內壓強的影響,現引入塑性極限內壓強的相對減小量

%,i=1,2,3,…

(60)

式中:ppi和pp,i+1分別為徑厚比增加前、后的塑性極限內壓強。

當α=1時,1號試件的徑厚比對塑性極限內壓強pp的影響如圖6所示。由圖6可知:厚壁圓筒塑性極限內壓強隨徑厚比的增大而逐漸減小;塑性極限內壓強的相對減小量Rd隨徑厚比的增大越來越小,且不同b值對應的2條曲線重合。

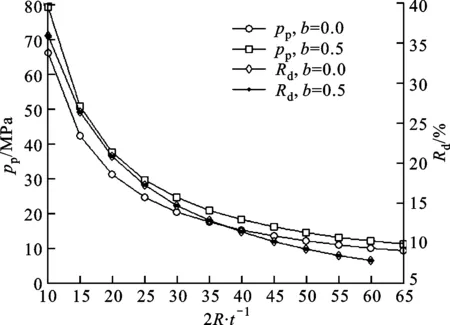
圖6　　　　厚壁圓筒1號試件的塑性極限內壓強與徑厚比的關系

為研究套箍指標的提高對縱向極限承載力的影響,現引入縱向極限承載力的相對提高量

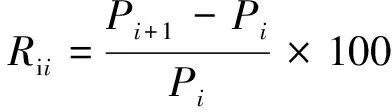
(61)

式中:Pi和Pi+1分別為套箍指標增加前、后的縱向極限承載力。

當α=1時,4號試件的套箍指標對縱向極限承載能力的影響如圖7所示。由圖7可知:套箍指標越高,厚壁圓筒縱向極限承載力就越大,表明提高套箍指標可以加強鋼管對核心混凝土的約束作用;隨套箍指標的提高,縱向極限承載能力的相對提高量逐漸變小。

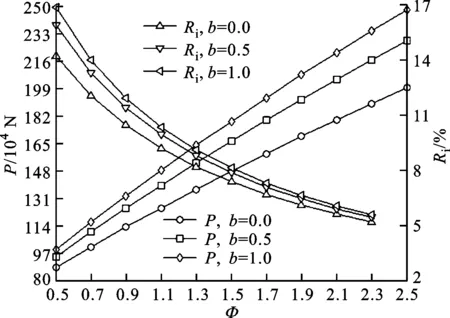
圖7　　　　厚壁圓筒4號試件的縱向極限承載力與套箍指標的關系

4.4　球殼彈性極限壓強的影響因素

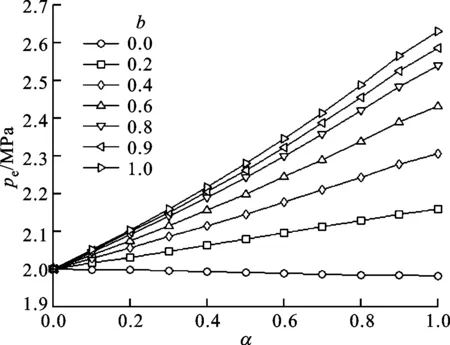
一承受內壓p的圓球形容器的內直徑d=2 000 mm,低碳鋼材料的抗拉強度σt=200 MPa,壁厚t=10 mm。拉壓強度比對彈性極限壓強的影響如圖8所示,可以看出球殼彈性極限壓強隨拉壓強度比的增大線性減小。

圖8　球殼彈性極限壓強與拉壓強度比的關系

4.5　球殼最小壁厚的影響因素

一承受內壓p=1.6 MPa的圓球形容器的內直徑d=2 000 mm,低碳鋼材料的抗拉強度σt=200 MPa。拉壓強度比對最小壁厚的影響如圖9所示,可以看出球殼最小壁厚隨拉壓強度比的增大而線性增大。

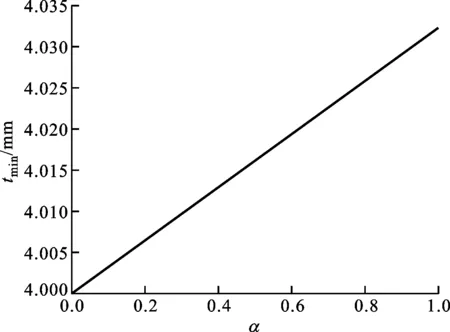
圖9　球殼最小壁厚與拉壓強度比的關系

5　結　論

本文考慮了圓筒和球殼的徑向正應力,按照俞茂宏統一強度理論求解了薄壁圓筒的彈性極限壓強和最小壁厚,并根據鋼管的橫截面面積與核心混凝土的橫截面面積,求解了厚壁圓筒的縱向極限承載能力,所得結論如下。

(1)薄壁圓筒彈性極限壓強隨中間主應力系數的增大而增大。當中間主應力系數很小時,薄壁圓筒彈性極限壓強隨拉壓強度比的增大而略微減小;當中間主應力系數較大時,薄壁圓筒彈性極限壓強隨拉壓強度比的增大而增大。

(2)薄壁圓筒最小壁厚隨中間主應力系數的增大而減小。當中間主應力系數很小時,薄壁圓筒最小壁厚隨拉壓強度比的增大僅有微小的增大;當中間主應力系數較大時,薄壁圓筒最小壁厚隨拉壓強度比的增大而減小。

(3)增加中間主應力系數或套箍指標都將增大厚壁圓筒的縱向極限承載能力。當中間主應力系數較小時,厚壁圓筒縱向極限承載能力隨拉壓強度比的增大而減小;當中間主應力系數較大時,厚壁圓筒縱向極限承載能力隨拉壓強度比的增大而增大。厚壁圓筒塑性極限內壓強隨徑厚比的增大而逐漸降低。厚壁圓筒縱向極限承載能力的計算值與試驗數據之間的相對誤差為-7.498 5%～7.106 0%。

(4)球殼彈性極限壓強隨拉壓強度比的增大而減小,球殼最小壁厚隨拉壓強度比的增大而增大,但球殼的彈性極限壓強和最小壁厚皆與中間主應力系數無關。

(5)本文所給出的公式可為承受內壓強的圓筒和球殼的分析計算提供一定的理論依據。

參考文獻:

[1]范文, 俞茂宏, 鄧龍勝. 巖土結構強度理論 [M]. 北京: 科學出版社, 2017: i.

[2]YU Maohong. Advances in strength theories for materials under complex stress state in the 20th century [J]. ASME Applied Mechanics Reviews, 2002, 55(3): 169-218.

[3]俞茂宏. 強度理論百年總結 [J]. 彭一江, 譯. 力學進展, 2004, 34(4): 529-560.

YU Maohong. Advances in strength theories for materials under complex stress state in the 20th century [J]. PENG Yijiang (translation). Advances in Mechanics, 2004, 34(4): 529-560.

[4]俞茂宏. 強度理論新體系: 理論、發展和應用 [M]. 2版. 西安: 西安交通大學出版社, 2011: 123-132, 145-148, 152-165.

[5]LIN Yuanhua, DENG Kuanhai, SUN Yongxing, et al. Through-wall yield collapse pressure of casing based on unified strength theory [J]. Elsevier Petroleum Exploration and Development, 2016, 43(3): 506-513.

[6]LIN Yuanhua, SUN Yongxing, SHI Taihe, et al. Equations to calculate collapse strength for high collapse casing [J]. ASME Journal of Pressure Vessel Technology, 2013, 135(4): 041202.

[7]LAW M, BOWIE G. Prediction of failure strain and burst pressure in high yield-to-tensile strength ratio linepipe [J]. Elsevier International Journal of Pressure Vessels and Piping, 2007, 84(8): 487-492.

[8]GüVEN U. Effects of different limit strength on plastic strains of thick walled pressure vessels [J]. Elsevier International Journal of Pressure Vessels and Piping, 2013, 104: 37-42.

[9]SUN Yongxing, LIN Yuanhua, WANG Zhongsheng, et al. A new OCTG strength equation for collapse under external load only [J]. ASME Journal of Pressure Vessel Technology, 2011, 133(1): 011702.

[10] XU Shuanqiang, YU Maohong. Shakedown analysis of thick-walled cylinders subjected to internal pressure with the unified strength criterion [J]. Elsevier International Journal of Pressure Vessels and Piping, 2005, 82(9): 706-712.

[11] 趙德文, 劉相華, 王國棟. 依賴Tresca和雙剪應力屈服函數均值的屈服準則 [J]. 東北大學學報(自然科學版), 2002, 23(10): 976-979.

ZHAO Dewen, LIU Xianghua, WANG Guodong. Yield criterion based on the mean function of Tresca and twin shear stress yield functions [J]. Journal of Northeastern University(Natural Science), 2002, 23(10): 976-979.

[12] 趙德文, 謝英杰, 劉相華, 等. 由Tresca和雙剪應力兩軌跡間誤差三角形中線確定的屈服方程 [J]. 東北大學學報(自然科學版), 2004, 25(2): 121-124.

ZHAO Dewen, XIE Yingjie, LIU Xianghua, et al. New yield equation based on geometric midline of error triangles between Tresca and twin shear stress yield loci [J]. Journal of Northeastern University(Natural Science), 2004, 25(2): 121-124.

[13] 趙德文, 張雷, 章順虎, 等. 用GM屈服準則解析薄壁筒和球殼的極限載荷 [J]. 東北大學學報(自然科學版), 2012, 33(4): 521-523, 532.

ZHAO Dewen, ZHANG Lei, ZHANG Shunhu, et al. Limit load of thin-walled cylinder and spherical shell with GM yield criterion [J]. Journal of Northeastern University(Natural Science), 2012, 33(4): 521-523, 532.

[14] 翟越, 魏雪英, 計琳, 等. 薄壁圓筒在雙剪統一強度理論下的統一解 [J]. 長安大學學報(建筑與環境科學版), 2004, 21(3): 1-3.

ZHAI Yue, WEI Xueying, JI Lin, et al. Unified limit solutions for thin wall cylinder based on twin shear unified strength theory [J]. Journal of Chang’an University(Architecture & Environment Science Edition), 2004, 21(3): 1-3.

[15] JIN Chengwu, WANG Lizhong, ZHANG Yongqiang. Strength differential effect and influence of strength criterion on burst pressure of thin-walled pipelines [J]. Springer Applied Mathematics and Mechanics(English Edition), 2012, 33(11): 1361-1370.

[16] 李子豐. 統一強度理論在桿管柱力學中的適用性和具有SD效應材料的安全應力域 [J]. 石油學報, 2016, 37(12): 1537-1542.

LI Zifeng. Applicability of unified strength theory in tubular mechanics and safety stress field of the material with SD effect [J]. Acta Petrolei Sinica, 2016, 37(12): 1537-1542.

[17] 劉鴻文, 林建興, 曹曼玲. 材料力學: Ⅰ [M]. 6版. 北京: 高等教育出版社, 2017: 225-228.

[18] 俞茂宏, 李建春. 新土力學研究 [M]. 武漢: 武漢大學出版社, 2017: 104-105.

[19] 俞茂宏, 昝月穩, 徐栓強. 巖石強度理論及其應用 [M]. 北京: 科學出版社, 2017: 146-147.

[20] YU Maohong, XIA Guiyun, KOLUPAEV V A. Basic characteristics and development of yield criteria for geomaterials [J]. Elsevier Journal of Rock Mechanics and Geotechnical Engineering, 2009, 1(1): 71-88.

[21] YU Maohong, KOLUPAEV V A, LI Yueming, et al. Advances in unified strength theory and its generalization [J]. Elsevier Procedia Engineering, 2011, 10: 2508-2513.

[22] 俞茂宏, 楊松巖, 劉春陽, 等. 統一平面應變滑移線場理論 [J]. 土木工程學報, 1997, 30(2): 14-26, 41.

YU Maohong, YANG Songyan, LIU Chunyang, et al. Unified plane-strain slip line field theory system [J]. China Civil Engineering Journal, 1997, 30(2): 14-26, 41.

[23] 丁敏, 汪友弟, 代春輝, 等. 鋼管混凝土軸心受壓構件的徐變預測模型及其徐變性能分析 [J]. 工程力學, 2017, 34(6): 166-177.

DING Min, WANG Youdi, DAI Chunhui, et al. Creep calculation and behavior analysis of concrete-filled steel tubular member under axial compression [J]. Engineering Mechanics, 2017, 34(6): 166-177.

[24] 錢稼茹, 李寧波, 紀曉東, 等. 外方內圓復合鋼管高強混凝土柱抗震性能試驗研究 [J]. 建筑結構學報, 2013, 34(5): 96-104.

QIAN Jiaru, LI Ningbo, JI Xiaodong, et al. Experimental study on seismic behavior of composite-sectioned high strength concrete filled steel tubular columns [J]. Journal of Building Structures, 2013, 34(5): 96-104.

[25] 俞茂宏. 材料力學 [M]. 2版. 北京: 高等教育出版社, 2015: 325-327, 364-367.

[26] 俞茂宏. 雙剪理論及其應用 [M]. 北京: 科學出版社, 2016: iv.

[27] 王卓. 厚、薄壁鋼管混凝土軸壓短柱承載力的統一解 [J]. 廣東建材, 2009, 25(6): 16-19.

[本刊相關文獻鏈接]

田紅亮,董元發,鐘先友,等.圓錐微凸體在粗糙表面接觸分析中的應用.2017,51(11):71-78.[doi:10.7652/xjtuxb2017 11011]

周曉松,梅志遠,張焱冰.夾芯復合材料T型接頭彎曲疲勞損傷機制及剩余強度試驗研究.2017,51(9):125-130.[doi:10.7652/xjtuxb201709018]

方斌,張進華,洪軍,等.聯合載荷作用下高速角接觸球軸承快速計算方法及接觸角分析.2017,51(6):115-121.[doi:10.7652/xjtuxb201706019]

方斌,張進華,洪軍,等.聯合載荷作用下高速角接觸球軸承快速計算方法及接觸角分析.2017,51(6):115-121.[doi:10.7652/xjtuxb201706019]

付曦,張俊紅,寇海軍,等.復雜載荷下軸流壓氣機葉片疲勞損傷數值研究.2017,51(5):149-155.[doi:10.7652/xjtuxb 201705021]

王慶朋,張力,尚會超,等.考慮應變硬化的混合彈塑性接觸模型.2016,50(2):132-137.[doi:10.7652/xjtuxb201602022]