運動的獨立性對于解決復雜曲線問題的誤區與反思
——基于物理核心素養的創新人才培養實踐經驗與啟示

陳 斌

（福州第三中學，福建 福州 350001）

一、運動的獨立性在物理教學中常見的誤區

運動的合成與分解是解決復雜曲線問題的一種重要方法，如何把復雜的曲線運動分解為已知的簡單運動是解決曲線運動問題的關鍵和難點，而這個過程的核心思想則依賴于運動的獨立性。例如，在司南版《必修2》中指出，“一個復雜運動可以視為若干互不影響的獨立的分運動”，并以平拋運動為例，通過實驗說明小球“在豎直方向上的運動與水平方向上的運動互不影響，是相互獨立的運動”。但是對于任何分運動是否具有獨立性并沒有說明，而是在教材中指出“這就是運動的獨立性”。受此影響，許多教師在平時教學過程中，往往僅通過幾類典型模型學生進行運動獨立性的引導，以至于大部分的學生在無意識中都形成了“任何一個運動的兩個分運動之間均具有獨立性”的刻板印象。這種刻板印象的形成，不僅讓學生在遇到一些復雜題目的時候很容易陷入思維定勢從而找不出破題要點，更重要的是，僅通過個別案例得到的結論不假思索地推廣成一個普遍性規律和原則，很容易讓學生喪失獨立思考和嚴密邏輯思維的能力，對于創新人才的培養是極為不利的。

因此，需要對“運動的獨立性”進行更深入地分析，以發掘其更深刻的內部規律！

二、運動的獨立性分析

（一）典例分析

2011年福建省理綜卷第22題考查了帶電粒子在復合場中的運動，尤其是對學生理解與運用運動的合成與分解，提出了比較高的要求。該題就運動的獨立性問題而言，是一道有代表性的題目，限于篇幅，文章主要就第（2）問進行討論。

（2011福建）（2）只改變入射粒子初速度的大小，發現初速度大小不同的粒子雖然運動軌跡（y—x曲線）不同，但具有相同的空間周期性，如圖乙所示；同時，這些粒子在y軸方向上的運動（y—t關

Ⅰ．求粒子在一個周期T內，沿X軸方向前進的距離S。

Ⅱ．當入射粒子的初速度大小為V0時，其y—t圖像如圖丙所示，求該粒子在y軸方向上做簡諧運動的振幅Ay，并寫出y—t的函數表達式［1］。

解析 對于第（2）問的兩個問題，可以按照牛頓運動定律列出一般式：

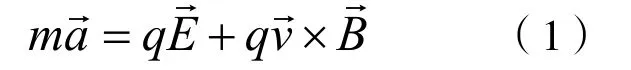
將帶電粒子沿x和y兩個方向分別列運動方程：

比較（2）（3）兩式發現，水平方向的運動包含了豎直方向的運動分量，豎直方向也是如此，這表明兩個方向上的分運動之間是相互影響的，這個結果與所謂的“運動的獨立性”是相違背的。此時如果要求出x和y的隨時間函數關系就需要去求解復雜的微分方程。

將（2）式對t求導并帶入（3）式vy，消去，得到關于vx一元微分方程：

（二）運動獨立性適用條件

上述分析表明，運動的獨立性是有前提條件的，它是建立在分運動各自滿足獨立方程，彼此之間沒有耦合項的基礎上，因此并不存在“運動的獨立作用原理”一說。實際上，通過查閱相關文獻會發現“運動的獨立作用原理” 來源于對力的獨立性的錯誤推廣，同時也是錯誤地把運用矢量分解研究問題的方法當作運動獨立性原理的依據。［2］

在弄清楚了運動的獨立性之后，就可以明白常見的物理模型中諸如平拋、帶電粒子在勻強電場中的偏轉，各個運動方向彼此無耦合項，在解題過程中其相關運動過程的物理量，例如加速度、速度、位移等，均可以分解到適宜的方向上，彼此之間相互獨立。但是對于類似文章所涉及的帶電粒子在復合場中的偏轉，又或者空氣阻力不能忽略的拋體運動等，一般情況下各運動分量之間是相互關聯的，雖然依然可以運用運動的合成與分解的方法進行求解，但在實際求解過程中則要求解復雜的微分方程，此時往往需要通過一些巧妙的方法找到相互獨立且比較簡單的分運動加以簡化計算。

（三）巧用運動獨立性解決復雜曲線問題

當然，如果學會巧用運動的獨立性，對于解題就會產生明顯的效果。還是以上述高考題為例，這里介紹一種巧用運動獨立性解題的方法。

必須指出的是，第二種方法雖然巧妙地將合運動分解為兩個相對簡單且獨立的分運動，但是這并不意味這對每一種復雜運動都適用。但是考慮到第一種方法在計算上的復雜性，也明確了出題者在命題時候一般會給出這種可以獨立分解的情況，那就可以給我們啟發，如果在進行運動的合成與分解之前先對運動獨立性進行分析，找到消除耦合項的約束條件，很多時候就可以像本題一樣找到快速解決問題的突破口。

三、運動獨立性分析對于教育教學的啟示

筆者認為，教學的邏輯與思維的邏輯、學科的邏輯應當是一致的，對于結構性很強的物理學科，更應體現科學的邏輯性，這才是中學生應該具備的核心素養。

這就要求，在進行運動合成與分解這部分內容教學時，應注意厘清合運動與分運動之間內在的關系，是建立在物理矢量在物理學中是以矢量運算法則、直角坐標、極坐標、自然坐標、球坐標、柱坐標等一整套數學體系基礎上表達出來的結果。［4］在教學過程中不能簡單將平拋或蠟塊等實驗的結果作為分運動獨立性的依據，而要引導學生思考為什么運動的合成與分解要提出獨立性要求，什么情況下能夠滿足獨立性要求。要深入挖掘如何分解才能夠滿足“簡便”這一教學過程中的重要邏輯樞紐，而分運動的獨立性正是在這一邏輯下的自然延伸，就如在案例分析中，正是考慮到分運動的獨立性，才可以避開求解繁瑣的微分方程，從而達到“簡便”的目的。學生知識邏輯的形成，尤其需要教師依據物理學的學科結構以及學生認知結構不斷去滲透與構建。

學生科學思維能力的形成，是培養創新人才最核心的要素之一。從學生知識建構的邏輯性出發，克服運動獨立性教學過程中的一些常見誤區，這是對基于核心素養的創新人才實踐的一種有益探索。

［1］福建理科綜合能力測試物理試題部分及參考答案［J］． 中學物理教學參考，2011（7）．

［2］楊習志，劉勁松．運動具有獨立性原理嗎［J］．物理教學，2015（11）．

［3］胡宗仁．“配速法”及其應用［J］,中學物理，2011（1）．

［4］胡揚洋．對“運動的獨立性”與“力的獨立作用原理”的再認識——兼論“平拋運動”教學的邏輯［J］．物理通報，2013（7）．