抓本質(zhì)悟思想 提升數(shù)學素養(yǎng)

謝秀蘭

（長樂區(qū)教師進修學校，福建 長樂 350200）

《義務(wù)教育數(shù)學課程標準（2011年版）》教學建議部分明確提出：“數(shù)學思想蘊涵在數(shù)學知識形成、發(fā)展和應(yīng)用的過程中，是數(shù)學知識和方法在更高層次上的抽象與概括。”由此，數(shù)學思想應(yīng)成為小學數(shù)學課堂教學的具體目標而加以落實，這就要求一線教師要研讀教材，努力挖掘提煉隱含于教材知識技能中的數(shù)學思想，讓數(shù)學思想顯現(xiàn)出來，抓住數(shù)學知識和數(shù)學思想兩條主線，并駕齊驅(qū)，促進學生數(shù)學素養(yǎng)的提升。如果說數(shù)學知識是數(shù)學的軀干，那么數(shù)學思想就是數(shù)學的靈魂，怎樣才能引領(lǐng)學生深入到數(shù)學的“靈魂深處”呢？筆者結(jié)合平時的聽課與思考，與大家作個交流。

一、在釋疑解惑處，領(lǐng)悟數(shù)學思想

著名物理學家李政道博士說：“什么是學問？就是要學怎樣問，就是學會思考問題。”［1］問題是數(shù)學的心臟，一切思維都是從問題開始的，正如愛因斯坦所言：“提出一個問題往往比解決一個問題更為重要。”因而，教師要注重培養(yǎng)學生的問題意識，鼓勵學生大膽質(zhì)疑問難，讓學生在質(zhì)疑問難中主動思考，積極求知，在思維碰撞中釋疑解惑，領(lǐng)悟數(shù)學思想方法，學會思考，學會學習。

例如，2017年10月29日，筆者在福州倉山小學有幸聆聽了浙江省特級教師顧志能老師執(zhí)教的四年級數(shù)學拓展課《九宮格的秘密》。上課伊始，顧老師播放《射雕英雄傳》視頻片段，從情境中引入探究問題：用1—9九個數(shù)字，放入九個格子中，要求無論橫的豎的斜的加起來的和都是15。學生明確題目要求后，自主擺卡片，顧老師展示了三位學生的擺法（如圖1、圖2、圖3），以及《射雕英雄傳》中黃蓉的口訣“二四為肩，六八為足，左三右七，載九履一，五居中間”以及郭靖擺的九宮格（如圖4），顧老師進一步引導學生觀察對比，并通過上下、左右交換和課件旋轉(zhuǎn)溝通不同方法之間的聯(lián)系。為了讓學生明白原理，顧老師說：“你們有什么想問的？”鼓勵學生質(zhì)疑問難，教師選擇有價值的問題板書在黑板上：①中間數(shù)為什么是5？②橫的豎的斜的，加起來的和為什么是15？③共有多少種擺法？④四個角都是雙數(shù)，單數(shù)可以嗎？對于第①個問題“中間數(shù)為什么是5？”換一種說法就是“中間數(shù)用其他數(shù)可以嗎？”，顧老師讓學生用“6”做實驗，先嘗試擺一擺，并請一個學生上黑板擺，可學生怎么擺都不成，這時顧老師及時引導，不能這么光做實驗，要動腦思考，能不能只拿一張卡片就能打敗這個問題？一語驚醒夢中人，學生從無序擺進入了有序思考，拿出卡片“9”，邊擺邊說明理由，不管9放哪格，與6的和是15，再加一個數(shù)就超過15了，所以中間擺“6”不行。顧老師緊追著問，中間擺“7”行嗎？學生稍作思考：那更不行了，9與7的和都超過15了，由此看來，比5大的數(shù)都不行了！顧老師繼續(xù)引導，那比5小的數(shù)行嗎？能不能也憑一張卡片就能打敗這個問題？學生通過嘗試、推理，得出比5小的數(shù)都不行。最后，顧老師小結(jié)，比5大的不行，比5小的也不行，就只能填“5”了，這過程就叫作推理。

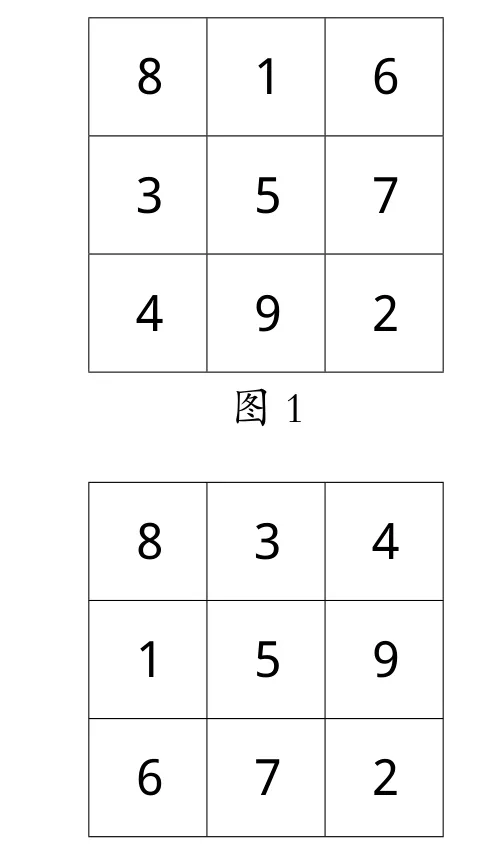
圖3

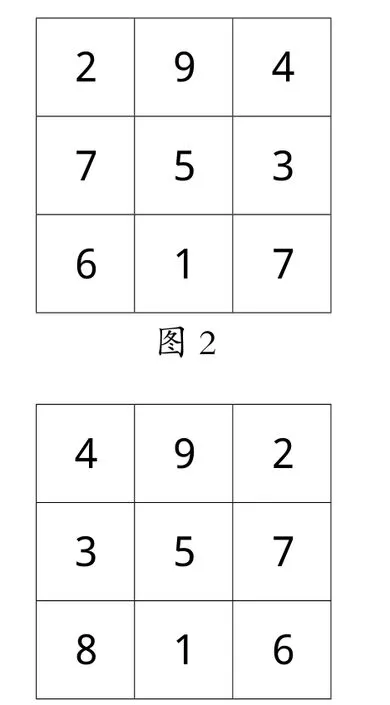
圖4

在“五居中間”的探秘過程中，顧老師把1—9九個數(shù)字分為“5”與“非5”兩類，通過擺“比5大的數(shù)”與“比5小的數(shù)”都不行，來證明只能擺“5”，讓學生體會反證法思想；顧老師先讓學生用“6”做實驗，從學生無序擺中引導學生思考，能否只拿一張卡片就能打敗這個問題，運用了舉例驗證的方法，讓學生體會有序思考的思想；以“6”作為例子，讓學生推想“7、8、9”行不行？以“比5大的數(shù)”不行，推想“比5小的數(shù)”行不行？讓學生領(lǐng)悟推理思想的魅力，學生在釋疑解惑中學會思考、學會學習，思維能力和數(shù)學素養(yǎng)都得到了提升。

二、在親歷過程中，體驗數(shù)學思想

數(shù)學思想方法總是伴隨著數(shù)學知識發(fā)生、發(fā)展的過程而顯現(xiàn)出來的，因而，教師應(yīng)想方設(shè)法讓學生親歷知識的形成過程，在過程中充分感知、體驗，加深對知識本質(zhì)的理解，同時對知識背后蘊含的數(shù)學思想方法有更深刻的體驗，從而提升學生的數(shù)學素養(yǎng)。

例如，人教版二年級上冊第六單元“7的乘法口訣”一課，許多教師以為教學乘法口訣只是為了快捷計算，于是，“熟記口訣”和“用口訣計算”便成了課堂教學的核心目標。其實，在看似簡單的乘法口訣教學中，卻蘊含著十分豐富的數(shù)學思想方法，需要教師們努力挖掘。曾聽過一位教師是這么設(shè)計的：以白雪公主和7個小矮人拼擺七巧板的童話引入，學生在欣賞和數(shù)數(shù)中明確了每個美麗圖案都是由7塊板拼成的，接著，教師借助數(shù)軸這個直觀模型，動態(tài)地呈現(xiàn)小矮人在數(shù)軸上站隊的畫面，并且每站上一個小矮人，就在落腳處點上一個點，標上相應(yīng)的數(shù)字或方框（如圖5），學生通過觀察小矮人站隊的全過程，清楚地看出數(shù)軸上的點與板塊數(shù)之間的一一對應(yīng)關(guān)系，“幾個7”的表象便清晰地呈現(xiàn)在學生頭腦中，為寫出乘法算式，理解乘法口訣的來源和含義奠定了基礎(chǔ)，學生從中感受到數(shù)形結(jié)合思想和一一對應(yīng)思想。當教師編出口訣“一七得七”后，讓學生說說這句口訣的含義，然后放手讓學生繼續(xù)編制口訣，并同桌互相說說每一句乘法口訣的含義，即說清每一句乘法口訣是“哪兩個數(shù)相乘的積是多少”，學生在遷移學習中，真實地經(jīng)歷著口訣的編制過程，加深了對口訣的理解，而口訣的理解又可幫助學生記憶口訣，提高有意記憶能力，同時，充分感受著類比推理思想的魅力。

圖5

三、在回顧梳理中，深化數(shù)學思想

數(shù)學知識具有很強的邏輯性和完整性，而小學數(shù)學教材的編排，充分考慮并尊重知識的難易度、小學生的心智特點與思維路徑漸進的特點，采取循序漸進、螺旋上升的形式編排。［2］因此，教師在實際教學時，不能只關(guān)注一冊教材的內(nèi)容、一個例題的教學目標，而應(yīng)該對同一個主題的教學內(nèi)容進行系統(tǒng)梳理，溝通新舊知識間的縱橫聯(lián)系，讓學生在感悟數(shù)學思想的同時，對某類知識有個系統(tǒng)全面的認識。

例如，2017年10月28日，筆者在福州倉山小學有幸聆聽了江蘇省特級教師周衛(wèi)東老師執(zhí)教的《確定位置》，周老師創(chuàng)設(shè)了以“救援故障船”的現(xiàn)實情境引入，扣人心弦，學生如臨其境，課堂氛圍緊張而熱烈，點燃了學生救援的責任和學習的熱情，效果非常好。當學生通過大膽猜想、自主探索，明白“方向、角度、距離”是確定位置的三要素后，周老師提出質(zhì)疑：“三個條件必須缺一不可嗎？”接著，他出示信息：1.南偏西，讓學生上臺在屏幕上圈出可能的區(qū)域；再出示信息。2.南偏西25度，讓學生上臺比劃一下可能在哪？最后出示信息。3.12千米，讓學生在屏幕上指出來。在這個質(zhì)疑驗證環(huán)節(jié)中，周老師采用層層遞進、步步追問的方式，讓學生在比劃中加深認識，如果只告訴方向，就只能確定物體可能在哪個“面”上，加上角度后就能確定它在一條“線”上，再告訴距離就能找到這個“點”。很好地溝通了“面、線、點”與“方向、角度、距離”之間一一對應(yīng)關(guān)系，感悟數(shù)形結(jié)合思想和模型思想，讓學生深刻認識到“確定位置”的過程本質(zhì)即是“由面到線，再到點”，學生的空間觀念、思維能力也得到鍛煉與提高。在課末，周老師還引領(lǐng)學生回憶確定位置的知識在小學階段一共接觸過幾次？然后大屏幕呈現(xiàn)一年級時學習的“上下前后左右、排第幾”；四年級學習的“第幾排第幾個，用數(shù)對表示”；今天學習的“用方向、角度、距離確定位置”。從一維到二維，用數(shù)對表示到學會用三要素確定位置，學生在回顧梳理中體會新舊知識的聯(lián)系，在感悟類比思想與模型思想的同時，實現(xiàn)對知識結(jié)構(gòu)的整體把握，學生的數(shù)學素養(yǎng)也得以提升。

四、在習題創(chuàng)編中，內(nèi)化數(shù)學思想

習題是例題的延伸和拓展，往往蘊含著豐富的知識、思想和方法，需要教師巧用、活用，把習題中所蘊含的數(shù)學思想方法挖掘出來，最大限度地發(fā)揮每道習題的功效，讓學生在操練中拓寬思路，感悟思想，掌握方法，提升素養(yǎng)。

例如，人教版三年級下冊“長方形、正方形面積的計算”一課，福清實小的林老師到長樂實小進行校際交流時，課尾設(shè)計的一道練習題給筆者留下深刻印象：“在方格紙中畫出面積是12平方厘米的長方形，要求先在頭腦中想象是怎樣的長方形？然后再畫出來。”學生呈現(xiàn)了三種情況：①長12，寬1；②長6，寬2；③長4，寬3。這時，教師利用課件，把長方形從①變成②再變成③，并鼓勵學生再想象，長方形的長和寬還可以是怎樣的？學生通過課件直觀演示與大腦想象，看到了長方形長、寬的變化，而面積不變，函數(shù)思想和極限思想深深地烙印在頭腦中，學生的思維能力、空間想象能力、數(shù)學素養(yǎng)都得到了培養(yǎng)與提升。

又如，人教版二年級上冊“乘法的初步認識”，在經(jīng)歷多個加數(shù)相同的加法算式可以改寫成乘法算式之后，有位教師把練習九第10題進行改造，設(shè)計了一組練習：

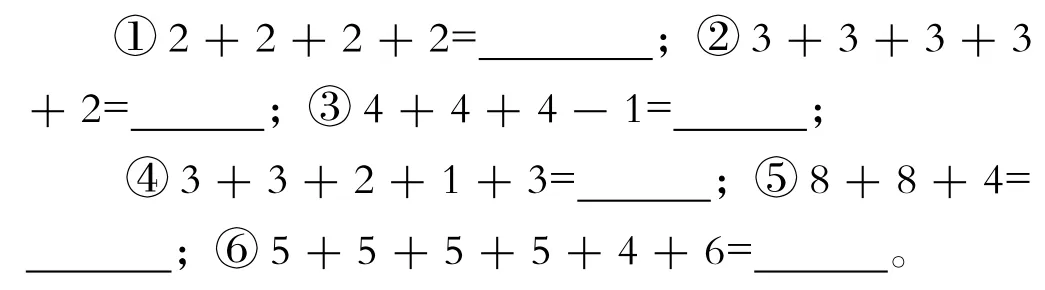
這6道題表面上看，好像只有第①題能改寫成乘法算式。于是，教師激發(fā)學生思考：哪些算式可以改寫成含有乘法的算式？哪些算式通過一些變動也能改寫成乘法算式？在教師的啟發(fā)下，學生把②③寫成了乘加、乘減的算式；學生通過觀察交流，發(fā)現(xiàn)可以把④⑤⑥中的一些數(shù)通過合并、拆分、調(diào)整等方法來改寫。學生從不能改寫到能改寫，打破思維定勢，抓住乘法意義的本質(zhì)，自覺尋找“加數(shù)相同”這個關(guān)鍵，既加深學生對乘法意義的理解，又從中領(lǐng)悟到變中不變的數(shù)學思想方法。

史寧中教授說：“數(shù)學思想是統(tǒng)領(lǐng)整個數(shù)學及數(shù)學學習的思想，是數(shù)學學科的基石。”［3］教師只有認真研讀教材，在觸及數(shù)學知識本質(zhì)的同時挖掘數(shù)學思想，雙線并聯(lián)共進，才能使課堂教學因顯現(xiàn)數(shù)學思想而有更高的立意，才能使學生發(fā)展成為具有時代氣息的有數(shù)學眼光和數(shù)學思想的人。

［1］席青城．如何培養(yǎng)學生提問意識［EB/OL］．［2017-10-10］． http ：//www．xzbu．com/9/view-5242578．html．

［2］劉延革．宏觀視角下分析和把握教材［J］．小學數(shù)學教師，2017（5）：76．

［3］史寧中．數(shù)學思想概論（第1輯）：數(shù)量與數(shù)量關(guān)系的抽象［M］．長春：東北師范大學出版社，2008．