巧用“變式教學”解高中數學疑惑

蔡汶劍

（漳州市第三中學，福建 漳州 363000）

章建躍在《數學教育心理學》中提到：變式就是變更對象的非本質特征的表現形式，變更觀察事物的角度或方法，以突出事物的本質特征，突出那些隱蔽的本質特征。這就要求教師在教學過程中，善于改造題目，充分利用一題多解，讓學生從不同的角度出發，對題目本身進行相應地理解以及挖掘。另一方面，也要求教師在教學過程中，循序漸進地對題目進行不斷地變式，由淺入深，讓學生充分討論以及探究，以便更好地答疑解惑。

一、變式教學的作用

所謂“變式教學”，是指教師從教學目標出發，設計一系列層層相扣的問題，由易到難，層層遞進，不斷地改變思考的角度，讓學生可以充分獨立思考，思維得到發散的一種教學方法。從2016年福建高考使用全國卷以來，數學文理科的難度和梯度都有所提升，很多題目必須深入理解才能真正得到答案，這就要求教師在教學過程中，加強題目的變式訓練，針對一題多解和一題多變，利用變式技巧將題目簡便化以及直觀化。巧用變式，讓學生對知識體系結構更加地清楚明了，也有助于學生自主探究能力的提升。

二、不同教學過程中的變式設計

變式教學中，教師要遵循針對性原則。所謂針對性原則是指從教學對象的實際認知發展水平出發，對于新授課、習題課、復習課列舉不同的變式題型以及方法。新授課的變式主要以完成教學目標為主，變式主要從教學目標出發；習題課的變式可以適當增加數學思想和方法；復習課的變式除了習題課的元素，還要注意發散思維，讓學生找出題目與題目之間的聯系與區別。另外，變式更要從教學對象出發，例如在高二文理分科之后，文科教學中，變式的難度和深度要明顯淺顯于理科，對于文科的學生，不宜一下子難度增加過大，對于一題多解的題目，可以結合代數法和幾何法從旁佐證再進行變式。

新授課是一種傳授新內容、講解新知識的授課。其在教學過程中，所占比重最大，學生主要通過新授課的教學，掌握新知識，聯系舊知識。學生對于新知識的掌握程度好壞主要取決于新授課，這就要求教師指導學生如何銜接新舊知識。下面以選修4-4的《極坐標系與參數方程》為例，例舉一題進行變式。

此題意在讓學生掌握極坐標系、參數方程、直角坐標方程之間的互化，作為新授課，此題的題干以及求解的兩個問題很好地體現了互化的問題，并且此題還跟以前所學習過的解析幾何進行了銜接，讓學生利用數形結合進行求解。在此基礎上，教師可以將再進一步進行變式。

例2：在直角坐標系XOY中，直線L的參數方程為（t為參數）在極坐標系（與直角坐標系XOY取相同的長度單位，且以原點O為極點，以x軸正半軸為極軸）中，圓C的方程為P＝4cosθ

（1）求圓C在直角坐標系中的方程；（2）若圓C與直線L相切，求實數a的值

習題課是通過對題目的講解實現學習效果的評價,以學生作業和練習為主要目的的授課。在習題課中，通過對習題的理解和練習，鞏固新知識，拓展新問題，展開剖析，讓學生結合教材知識點，提取相關的信息，遷移知識，構建體系，強化方法和規律技巧。讓學生學會思考、學會分析，舉一反三。所以，習題課的課時雖然不多，但在課堂教學中起著舉足輕重的作用。

此題是求三角函數最值的問題，教師在學生掌握三角函數化一公式的基礎上進行講解，并通過數形結合讓學生直觀上看出函數的最大值以及最小值。在此基礎上，可再加入二倍角公式的應用，以及換元的思想，逐步加深，讓學生在充分理解三角函數公式的基礎上，強化數形結合的思想。

復習課是以總結知識規律，總結答題規范和方法技巧，總結學習方法，進行反思的授課。所以復習不是簡單的重復，需要在原有的基礎上進行總結，挖掘教材、拓展教材以加深理解。

三、不同教學對象的變式設計

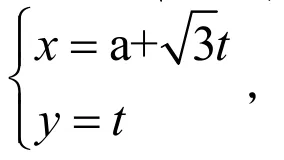
下面以立體幾何——2017年全國卷I第17題為例，提出教師針對不同教學對象如何設置不同的變式設計：

在高中階段，立體幾何是必修二的內容，教學對象為所有的高中生。立體幾何是歷年高考的重要考點，學生在初中只接觸過平面幾何的內容，對于立體幾何的內容是完全陌生的。但到了高中階段，學生的思維能力得到迅速發展，空間想象能力和抽象邏輯思維也得到很大的提高。在必修二的內容中，立體幾何適用于所有的學生，但到了高二文理分科之后，理科在必修二的基礎之上，多了空間直角坐標系的內容，于是理科生有更多的方法來解答立體幾何，并且相對于文科生，理科生的空間想象能力略高于文科生，因此在本題的設置中要抓住文理科的共同點和不同點進行相應的變式。

高考中，立體幾何的線線垂直、線面垂直、面面垂直的性質定理是重點也是難點。并且此內容是必修二的內容，在文理分科之前學生都應掌握理解，因此，在此題第一問的設計上，可從文理科的公共點出發設置疑問，如下：

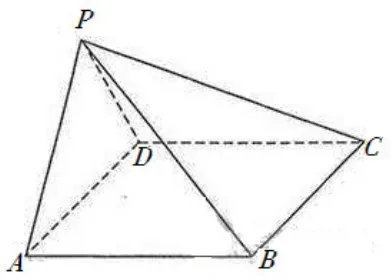
例6：如圖，在四棱錐P-ABCD中，AB//CD，且∠BAP=∠CDP=90°

證明：平面PAB⊥平面PAD

在第二問的設置上，可從學生的接受程度進行變式，文科的題目可從表面積、體積、高等問題提出疑問，理科的題目可在文科的基礎上，再增加線面所成的角、二面角的夾角大小問題進行變式。因此，第二問的設置上，文科可變式為：

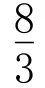
而對于理科，可將第二問變式為：

（2）若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值。

此題目的設置主要是針對文理科學生學習的接受程度，知識的掌握程度不同，而將題目的問題進行變式。對于文科而言，如何利用體積轉化為底面積、高、側面積等是學生需要掌握的重點，同時也是一大難點。很多學生立體感比較強，可以借助高來求解，而對于立體感較弱的學生，則可通過等體積法得到求解。對于理科而言，在選修中多了空間坐標系，于是，更多的學生會選擇建系的方法，從而把看似復雜的問題簡單化。教師在教學過程中，要針對近幾年全國卷的特點，分析文理差異，在此類型中多做變型和拓展，也可將錐變式為球或者柱再讓學生加以練習。

在教學過程中，教師要從教學目標出發，研究教學對象，提出合適的變式教學的內容。在變式教學過程中，如何把握變式教學的數量、質量、梯度是教師今后應該加強和提高的地方。巧用變式教學，讓學生主動參與教學過程中，體現其主體地位，可激發學習熱情，更可以提高學生的素質能力，起到答疑解惑的作用。

［1］孟令奇,張德利.跨文化視角下的中國數學教育特點探析——到底什么是中國式的數學教學［J］.數學教育學報，2013（12）.

［2］肖凌戇.數學教育要以理性思維育人——我的數學教學主張［J］.中國數學教育，2016（5）.

［3］劉勤，何長林.去其浮華，挖掘數學教育的本質——一堂高三“等差數列復習課”的教學實錄與改進［J］.數學教學通訊，2015（12）.