數(shù)學(xué)分析中數(shù)學(xué)結(jié)構(gòu)的層次關(guān)系

高婷婷，張明會(huì)

（隴南師范高等專科學(xué)校，甘肅成縣742500）

數(shù)學(xué)分析中數(shù)學(xué)結(jié)構(gòu)的層次關(guān)系

高婷婷，張明會(huì)

（隴南師范高等專科學(xué)校，甘肅成縣742500）

在對結(jié)構(gòu)思想概括介紹的基礎(chǔ)上，進(jìn)一步揭示了整個(gè)數(shù)學(xué)體內(nèi)的結(jié)構(gòu)層次關(guān)系。提出整個(gè)數(shù)學(xué)是建立在集合的基礎(chǔ)上。首先是集合，一旦在集合的元素之間引進(jìn)了一些關(guān)系，集合的元素就有了自己的個(gè)性和特征，然后再根據(jù)關(guān)系的性質(zhì)，在集合上形成結(jié)構(gòu)。

數(shù)學(xué)分析；數(shù)學(xué)結(jié)構(gòu)；層次；分析

1 數(shù)學(xué)結(jié)構(gòu)的層次框架

布爾巴基在集合上首先建立了三個(gè)基本結(jié)構(gòu)：即代數(shù)結(jié)構(gòu)、序結(jié)構(gòu)和拓?fù)浣Y(jié)構(gòu)，并稱它們?yōu)槟附Y(jié)構(gòu)。然后，在母結(jié)構(gòu)的基礎(chǔ)上，根據(jù)“親緣”關(guān)系，交叉產(chǎn)生新的邊緣結(jié)構(gòu)；或者由二個(gè)以上母結(jié)構(gòu)聯(lián)合產(chǎn)生復(fù)合結(jié)構(gòu)；或者在一個(gè)母結(jié)構(gòu)上加上一些公理產(chǎn)生新的子結(jié)構(gòu)。這樣通過結(jié)構(gòu)的反復(fù)交叉、復(fù)合、變換，形成了各種各樣的數(shù)學(xué)分支，從而就形成一個(gè)有內(nèi)部結(jié)構(gòu)的整個(gè)數(shù)學(xué)世界。

布爾巴基以三個(gè)母結(jié)構(gòu)為中心，按照結(jié)構(gòu)交叉、復(fù)合、變換，將整個(gè)數(shù)學(xué)系統(tǒng)由一個(gè)分支發(fā)展到另一個(gè)分支，由一個(gè)層次延伸到另一個(gè)層次，一直延伸到未開墾的處女地。其結(jié)構(gòu)層次框圖如圖1所示。

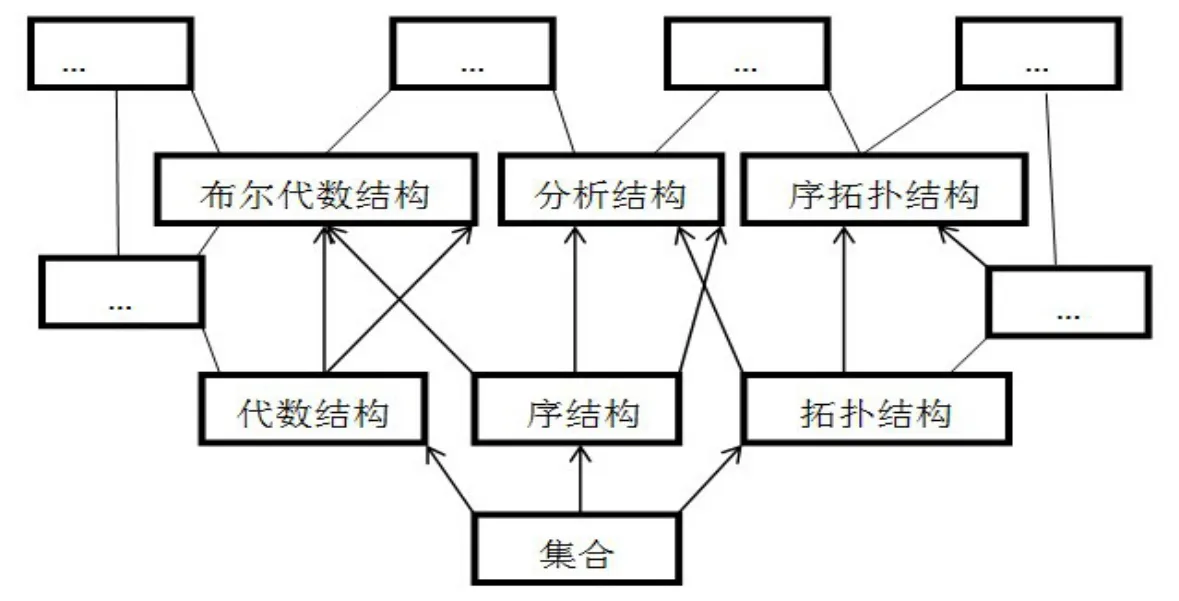
圖1 布爾巴基數(shù)學(xué)結(jié)構(gòu)層次圖

2 母結(jié)構(gòu)簡介

由于母結(jié)構(gòu)是整個(gè)數(shù)學(xué)結(jié)構(gòu)的核心，又是實(shí)數(shù)R結(jié)構(gòu)的基礎(chǔ)，所以揭示實(shí)數(shù)R結(jié)構(gòu)的特征之前，必須對三個(gè)基本結(jié)構(gòu)有所了解。

2.1 代數(shù)結(jié)構(gòu)

集合上建立了運(yùn)算（來自數(shù)量關(guān)系），就能夠從兩個(gè)元素生出第三個(gè)元素，從而在此基礎(chǔ)上就產(chǎn)生了代數(shù)結(jié)構(gòu)。具體地講，由離散對象、代數(shù)運(yùn)算及其公理組所構(gòu)成的結(jié)構(gòu)系統(tǒng)統(tǒng)稱為代數(shù)結(jié)構(gòu)。例如，大家熟知的群、環(huán)、域、線性空間等。下面僅就域的結(jié)構(gòu)為例作簡要介紹。

L(T)：＜R；+，?＞滿足下列公理：

L1:R中的所有元素關(guān)于代數(shù)運(yùn)算“+”滿足結(jié)合律，即

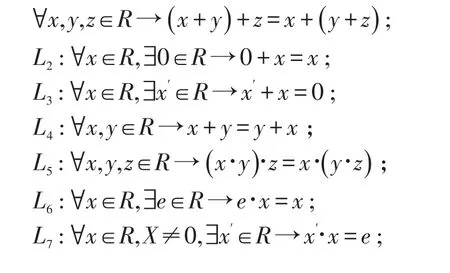
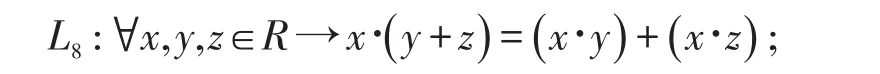
則稱代數(shù)結(jié)構(gòu)＜R；+，?＞為域。

2.2 序結(jié)構(gòu)

集合中某些元素有先后順序關(guān)系（來自時(shí)間觀念），從而在此基礎(chǔ)上就產(chǎn)生了序結(jié)構(gòu)。具體地講，由集合中的序關(guān)系及其公理組所構(gòu)成的數(shù)學(xué)結(jié)構(gòu)稱為序結(jié)構(gòu)。例如，數(shù)的大小關(guān)系，生物的親緣長幼關(guān)系，類的包含關(guān)系等。下面就全序和半序結(jié)構(gòu)分別作簡要介紹。

2.2.1 全序結(jié)構(gòu)

L(T):＜A；R＞如滿足下列公理：

L1：A中的元素關(guān)于關(guān)系R具有“自反性”，即

x∈A→xRx；

L2：A中的元素關(guān)于關(guān)系R具有“反對稱性”，即

?x,y∈A,若 xRy且 yRx，則 x=y；

L3：A中的元素關(guān)于關(guān)系R具有“傳遞性”，即

?x,y,z∈A,若 xRy且 yRz，則 xRz；

L4:A中的任意兩個(gè)元素關(guān)于關(guān)系R具有“可比性”，即

三種可比性關(guān)系中有且僅有一種成立。所以可比性亦稱“三歧性”或“三分律”。則稱數(shù)學(xué)結(jié)構(gòu)＜A；R＞為全序結(jié)構(gòu)。

例如，自然數(shù)集N,關(guān)于關(guān)系“≤”滿足全系公理，所以數(shù)學(xué)結(jié)構(gòu)＜N；≤＞是一個(gè)全序結(jié)構(gòu)。

2.2.2 半序結(jié)構(gòu)

L(T):滿足全序結(jié)構(gòu)前三條公理的數(shù)學(xué)結(jié)構(gòu)＜A；R＞稱為半序結(jié)構(gòu)。

顯然，半序集再加上可比性就是全序集。正因?yàn)榘胄蚣艑捔艘螅赃m應(yīng)范圍就比全序集廣。

2.3 拓?fù)浣Y(jié)構(gòu)

所謂拓?fù)浣Y(jié)構(gòu)，就是用來描述集合元素的連續(xù)性、分離性、臨近、邊界（這些概念來自空間經(jīng)驗(yàn)）性質(zhì)的數(shù)學(xué)結(jié)構(gòu)。

由于拓?fù)浣Y(jié)構(gòu)是指能夠描述極限和連續(xù)性的那種數(shù)學(xué)結(jié)構(gòu)，而極限和連續(xù)性又是建立在領(lǐng)域概念的基礎(chǔ)上的，因此，為了在一般意義上進(jìn)行拓?fù)涓拍睿环N比較直觀而較簡單的辦法是引進(jìn)鄰域和鄰領(lǐng)域結(jié)構(gòu)。

L1：A中的每一個(gè)元素x在鄰域集B中至少有一個(gè)包含它的鄰域ux，即

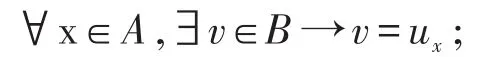
L2:A中的任一個(gè)元素在B中的任何兩個(gè)鄰域之交仍是該元素在B中的一個(gè)鄰域，即

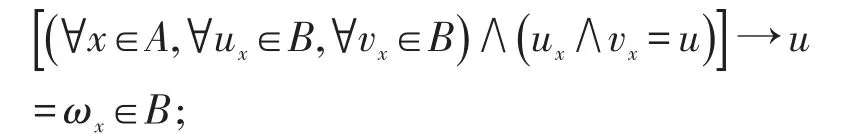
L3:若V是A的一個(gè)子集，而A中元素x的一個(gè)鄰域ux又是v的子集，則v必是B中x的一個(gè)鄰域，即

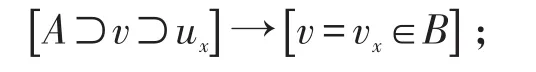
L4：A中任何一個(gè)元素x的任何一個(gè)鄰域ux中必含有x的一個(gè)鄰域vx,使得當(dāng)A中的元素y∈vx時(shí)，總有 vy∈vx，即

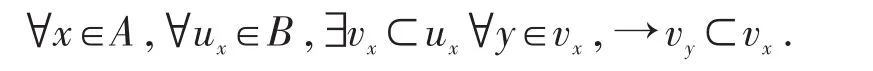
根據(jù)上述四條公理，就能保證在數(shù)學(xué)分析的論域內(nèi)任一點(diǎn)x，能選取一連串越來越小的鄰域使之以點(diǎn)x為極限。因此，鄰域公理系統(tǒng)可以導(dǎo)致極限概念。正是由于鄰域公理系統(tǒng)能描述極限和連續(xù)，而拓?fù)渥儞Q正好是研究在變換下連續(xù)性不變的那種變換。所以，人們亦稱公理系統(tǒng)為拓?fù)浣Y(jié)構(gòu)。

On the Hierarchical Relationship of Mathematical Structure in Mathematical Analysis

GAO Tingting，ZHANG Minghui
(Longnan Normal College Department of mathematics,Gansu 742500，China)

This paper in the structure thought is summarized and introduced based on,further reveals the whole mathematics in vivo hierarchy.Put forward the mathematics is built on the basis set.First is set,once between the elements of the set introduced some relationship,elements of the set have their own personality and characteristics,and then according to the nature of the relationship,in the collection structure formation.

mathematical analysis;mathematical analysis;structural level;analysis

郝安林）

0151.2

A

1673-2928（2018）02-0093-02

D01:10.19329/j.cnki.1673-2928.2018.02.026

2017-01-03

高婷婷，女，甘肅禮縣人，隴南師范高等專科學(xué)校講師，研究方向：基礎(chǔ)數(shù)學(xué)。