無差別原則相關悖論多解的本質意義
——以酒水悖論、貝特朗悖論為例

趙　曼

(1.中國社會科學院研究生院， 北京　102488； 2.澳大利亞國立大學, 堪培拉　ACT0200)

一、無差別原則

無差別原則是邏輯解釋確定初始概率的基本原則。古典概率論的基礎是伯努利(Jakob Bernoulli)的“不充足理由原則”(The Principle of Non-sufficient Reason)，即在某一條件下的任意一個隨機事件，我們如果沒有足夠的理由認為他們其中的某些情況比另外的一些情況更有可能發生，那么就認為它們應該具有相等的概率。對于古典概率論的邏輯解釋就是依據此原則來確定基本事件的概率的。凱恩斯(John Maynard Keynes)將這一解釋的核心內容稍加修正后稱為“無差別原則”(The principle of indifference)[1]。然而，有時使用這個原則會導致邏輯悖論的出現。拉普拉斯(Pierre-Simon Laplace)就給出了下面的例子：假定一位女士投擲硬幣，雖然不知道硬幣會偏向哪一面但是被告知硬幣是有偏向性的，現在要求這位女士說出投擲后這枚硬幣正面向上的概率[2]。由于她對這枚硬幣更可能哪一面向上的問題是完全不知道的，那么她根據無差別原則判斷出這個硬幣正面向上和反面向上的概率相等，均是1/2。可是，既然她已經知道這枚硬幣是有偏向性的，那么她也可以判斷這枚硬幣正面向上的概率不是1/2。這兩種不同的思路就會帶來悖論，也就是說如果用P表示這枚硬幣正面向上的概率，那么我們就會有兩種相反的答案：P=1/2和P≠1/2。由無差別原則所導致的邏輯悖論層出不窮，而這些悖論被統稱為無差別原則悖論。如果要使用無差別原則來對概率的結論進行測度，就不得不對產生的悖論進行更多的思考。顏青山提到，根據不同的性質對無差別原則悖論進行區分：投擲硬幣的悖論等劃分為離散情形，貝特朗悖論、酒水悖論等劃分為連續情形[3]。下面我們將從兩個極具代表性的無差別原則悖論，即酒-水悖論和隨機弦悖論出發，審視同為連續情形的兩個悖論是否由于誤用了無差別原則而導致多解，同時分析在這兩個悖論下得到多解的本質原因是否相同。

二、酒水悖論及其多解分析

酒水悖論是說，假設有一瓶酒和水的混合液體，對于這瓶混合液體我們只知道其中兩種液體的比值不會超過3∶1，至于兩者之間哪個多，哪個少以及其他的信息一概不知道。由此，我們能夠確定酒對于水的比例落在區間[1/3，3]，也就是說 1/3≤酒/水≤3，但是這個比例到底在區間的哪個點上，我們并沒有辦法確定。由無差別原則可得，酒對水的比例的概率是均勻地分布在[1/3，3]這個區間的。因此，酒對于水的比例不超過2的概率也是均勻分布在 [1/3，2] 區間的。于是，可以得到下面的式子：

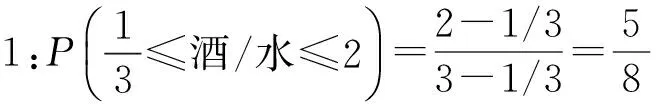
同理，可以知道水對酒的比例也是在區間[1/3，3]，即1/3≤水/酒≤3，并且其概率也是均勻地分布在該區間。那么，水對酒的比例不小于1/2的概率均勻地分布在區間 [1/2，3]。可以得到下面的式子：

酒對水的比例在區間[1/3，3]不大于2和水對酒的比例在區間[1/3，3]不小于1/2描述的是同一個事件。但是，通過以上的分析可知，使用無差別原則得到的兩個概率值卻是截然不同的，顯然15/16≠5/8，這就產生了悖論。

接下來我們來分析所得概率值的錯誤原因。當計算酒對水的比例不超過2的概率時，得到公式1，其中分子2-1/3和分母3-1/3不能直接進行比的運算。因為分子分母都分別是酒水比值的減法運算，上下得到的兩個差值的基準是不一樣的，因此對差值直接進行比的運算就是毫無道理的。研究的出發角度不同，就會產生不同的結果，看似產生了悖論，實則酒水悖論中的兩個結果都是錯誤的。如果想要正確地自始至終地運用無差別原則，那么就要找到一個不變的基準。筆者發現不管什么時候，V水+V酒=V這個等式都是不會發生變化的，因為不管比例如何它們總的體積是一瓶。也就是說隨著酒水比例的變化，它們相應的體積也就發生了變化(此處討論的時候，假設的前提是它們的體積不會因為相容而使得V發生微小的變化)。那么這個概率式子應該是這樣的：

其中V水1表示的是酒∶水=1∶3時候的V水；V水2表示的是酒∶水=2∶1時候的V水；V水3表示的是酒∶水=3∶1時候的V水。通過上述形象的概率式子，不難發現如此的比值，分子分母是不能互相抵消掉V水的，因為只有V水+V酒=V是不變的，其他的都是變量，酒水在不同的比值下，作為參照的水的體積已經發生了變化，那么在上式中，V水1≠V水2≠V水3是不能夠相互抵消的。所以說在區間內，隨著酒水兩者比值的變化，V水在不斷發生變化。同理，水對酒的比例不小于1/2的概率得到的公式2的計算方法也是錯誤的。

由以上兩種算法得到的兩個概率值均是不正確的，所以一直以來學者們認為這是個悖論問題，實則兩個都是不正確的算法。筆者嘗試將這個問題的分析形象化，同時求得酒水問題正確的概率值。如圖1—圖4所示：首先酒和水的總體積V是不變的，并且兩種液體的比值不會超過3∶1，于是我們來討論酒對水的比例不超過2的時候體積V是如何分配和變化的。圖1表示的是，酒∶水的最小比例1∶3；圖2表示的是，酒∶水的比例2∶1；圖3表示的是，酒∶水的比例不超過2時可變化的體積Vx；圖4表示的是，酒∶水的最大比例3∶1。通過圖形，我們可以清楚地看到，酒的可變體積在Vx表示的范圍內，一旦這個變化范圍內的酒的體積確定了，那么隨之水的比例也就得以確定了。所以，筆者認為由無差別原則可知，酒對水的比例在區間[1/3，3]時，酒的可變體積Vx在變化范圍 [1/4V，3/4V]是均勻無差別的，當酒對于水的比例不超過2時，酒的可變體積Vx在變化范圍 [1/4V，2/3V]是均勻無差別的。

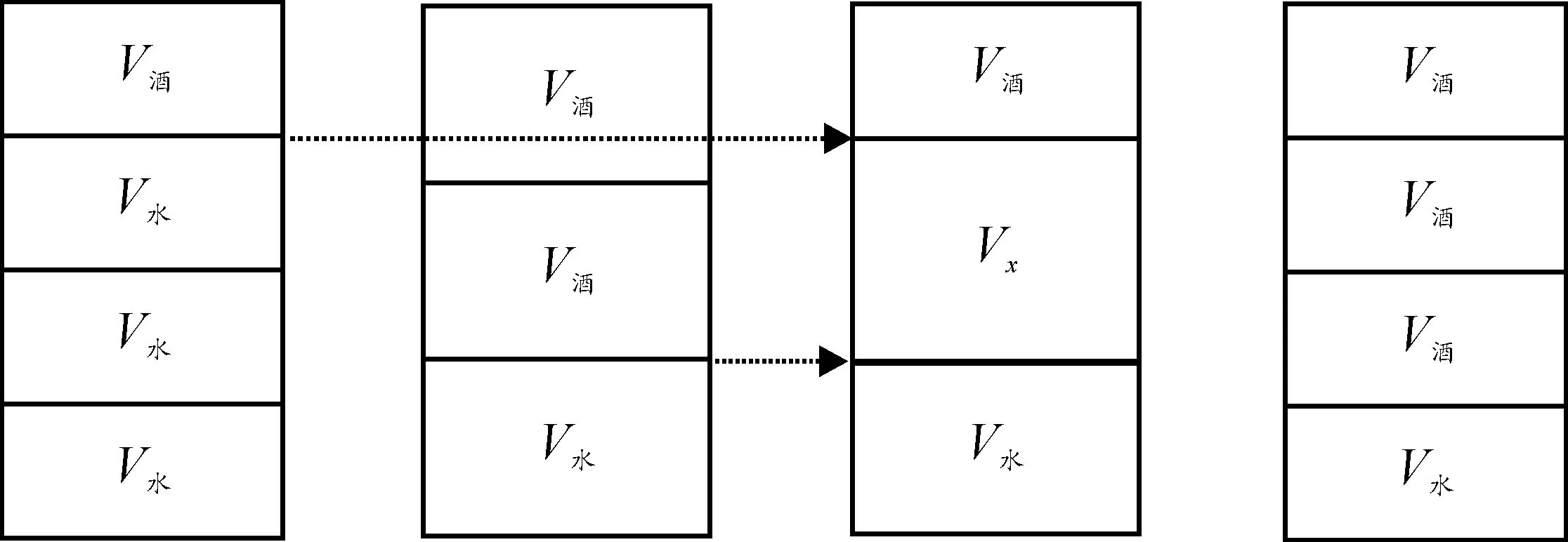
圖1 圖2 圖3 圖4

通過以上圖解，酒對于水的比例不超過2的概率可以得到：

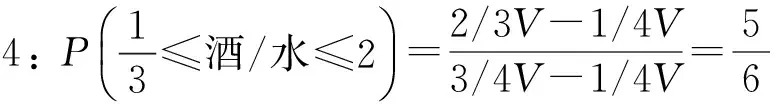
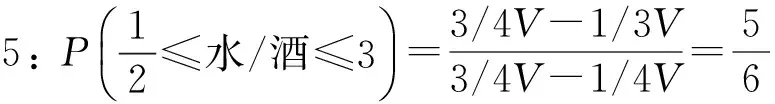
我們得到了兩個相同的結果，5/6就是酒水問題正確的概率值。

酒水問題中通過運用無差別原則得到了兩個不同的解，且得到的兩個解均是錯誤的。導致多解錯誤的本質原因就是在運用無差別原則的整個過程中，對酒水或水酒比例的概率運用了無差別原則，雖然分子分母單獨拿出來討論時，酒水或水酒比例在區間內都是均勻分布的，但是因為它們沒有選取到一個不變的基準，所以在運算的過程中將分子分母上不同的變量當作同一變量進行約分，就會得到一個看似正確實則錯誤的答案，然后說兩個錯誤的解產生了悖論就沒有意義了。筆者嘗試性地將不變的V作為基準，且考慮到酒水或水酒的體積比在區間內是均勻分布的，所以可以對Vx運用無差別原則，從而得到正確且統一的答案。

三、貝特朗悖論及其多解分析

約瑟夫·路易斯·貝特朗(Joseph Louis Bertrand)在其著作中構設了一個幾何概率悖論：“在一個圓內任意選一條弦，這條弦的弦長長于這個圓的內接等邊三角形的邊長的概率是多少？”[4]貝特朗就提出的這個問題從3個可行的角度給出了3個不同的概率值。下面我們就貝特朗給出的3種經典的解進行逐個分析，并對存在的其他的解舉一例來分析(圖5—圖7)。

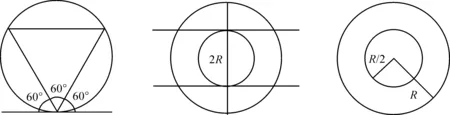
圖5 圖6 圖7

第一種答案，從端點方面來思考，如圖5所示。從圓周上選取的兩個端點來繪制連接為弦。通過想象，內接等邊三角形不停地旋轉，當它的頂點與其中一條弦的一端重合，另一端位于三角形另外兩個頂點之間的圓弧上時構成的弦比三角形的邊長長。也就是圓內接等邊三角形的夾角為60°，那些弦長長于內接等邊三角形邊長的弦一定都落在了三角形頂角的60°范圍內。而從頂點出發落于頂角以外的弦的弦長都比等邊三角形的邊長要短。我們沒有理由說明從三角形頂點出發的弦的另一端點在圓周上的某一個點而不是其他點，所以應用無差別原則可以得到(是弦與圓切線的夾角)：

公式6：P1=P(60°<θ<120°)=60°/180°=1/3

Martin設計了試驗驗證第一種答案的概率值[5]。任取一個圓，在圓的中心點位置固定一個類似于轉盤樣子的微調器，將兩個分別獨立旋轉的結果標記，作為弦的兩個端點；然后將實驗結果記錄；計算記錄下的結果，滿足的弦得到的概率值是趨近于1/3。

在這種解法中，先固定一點作為弦的一端，然后在圓周上隨機選取另外一點作為弦的另一端。陳作清將此方法擴展后提出，兩個端點在圓上均是隨機地進行選擇，通過幾何計算仍舊可以得到1/3的概率[6]。得到P1概率值的前提是將弦的兩個端點確定弦作為隨機弦的選取方式，也就是滿足條件的弦的另一端的范圍所在的弧長是圓周長的1/3，該種解法其本質是“隨機端點”即對端點在圓周上分布運用了無差別原則。

第二種答案，從半徑方面來思考，如圖6所示。在圓的一條半徑上隨機選擇一個點，過該點構造一條垂直于此半徑的弦，改點即是弦中點。圓內弦長長于內接等邊三角形邊長的那些弦的中點到該圓圓心的距離要小于該圓半徑的一半，弦中點到圓心距離來看，上、下半圓內分別可以劃分出兩部分1/2R的區域(圓半徑為R)。當弦中點到圓心的距離大于1/2R時的弦的弦長均小于內接等邊三角形的邊長。我們無法說明弦的中點在半徑的某一點上而不在其他點上，根據無差別原則可以得到：

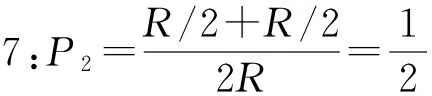
Edwin T.Jaynes給出了一個實驗來驗證第二種答案的概率值[7]。將一個直徑5英寸的圓畫在地板上，然后從某個固定的點將掃把枝隨機地拋擲，對128次成功拋擲的實驗結果進行計算，在誤差允許的范圍內得出的概率值為1/2。

在這種解法中，先要選取一條半徑，然后在半徑上任取一點作為弦中點。得到概率值的前提是將用弦中點確定弦的方式作為隨機弦的選取方式，其本質是“隨機半徑”即對弦中點在半徑上隨機分布運用了無差別原則。

第三種答案，從弦中點方面來思考，如圖7所示。在大圓內任意選取一個點作為弦的中點。在大圓的內接等邊三角形內再畫出一個三角形的內接圓，分別與三角形三邊相交。由數學知識我們可以得到這兩個圓是同心圓，且小圓的半徑為1/2R即大圓半徑的一半(大圓半徑為R)。當弦中點在小圓內時，對應的那些弦的弦長長于等邊三角形的邊長。反之，當弦中點在小圓外時，弦長必然小于邊長。我們沒有理由說弦的中點落在小圓內的某一點而不是其他的點，所以依據無差別原則可以得到：

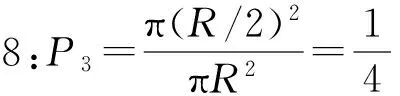
Martin用試驗來驗證第三種答案的概率值[5]。在材質上畫出一個圓，將整個圓用蜜糖覆蓋，從而引得蒼蠅隨機地落在蜜糖范圍內。蒼蠅首次落下的點作為一條弦的弦中點。反復記錄后，整理計算滿足條件的弦長出現的概率，得到的概率值是趨近于第三種答案的1/4。

在這種解法中，不作任何假設，直接任取一點作為弦中點。得到P3概率值的前提是將弦的中點在大圓內隨機分布等價為隨機弦的選取方式，其本質是“隨機中點”即對弦中點運用了無差別原則。

通過分析，我們可以發現貝特朗在悖論中給出的3種經典答案均得到了可操作性的真實實驗的驗證，且3種答案在各自運算的過程中從不同方面分別運用了無差別原則。

陳曉平[8]在吉利斯[7]對使用無差別原則提出限制條件的觀點上進一步給出了線性無差別條件：如果參數θ在一個區間的概率分布是無差別的，且Φ=f(θ)是一次函數，那么可以得到Φ在相應的區間的概率分布也是無差別的。我們從圖像上就可以更清晰地看到：如圖8所示，當θ在橫坐標的區間[a，b]勻速運動的時候，它投射到任何一條斜線上的點在相應的區間[a，b]也是勻速運動的，如果投射到的不是斜線而是曲線上的話，如圖9所示，在曲線上的動點就不再是勻速運動了。所以，要想θ和f(θ)使用無差別原則就需要它們之間的關系是線性的。

圖8 圖9

按照陳曉平的觀點，在第一種答案里，除三角形頂點外的另一弦端點與頂點處圓切線的夾角形成的角度和弦中點到圓心的距離之間是三角函數關系，不是一階線性的，所以該答案的計算錯誤地運用了無差別原則。而在第三種答案里，弦中點到圓心的距離與其中點分布的圓的面積之間是二階的函數關系，也不是一階線性的，所以也是錯用了無差別原則而得到的錯誤答案。筆者認為其實不然，3種答案分別是將無差別原則運用于端點在圓周上分布時、弦中點在半徑上分布時、弦中點在圓內分布時得到的。分別運用無差別原則時均沒有產生錯誤，所以導致貝特朗悖論的本質原因并不是無差別原則的錯誤運用。那么究竟是什么導致的悖論呢？其實，是對所提出的問題審讀時對隨機選取弦的方式理解不同才導致了不同的結果，即前提不同。P1值時，端點是隨機分布的，但此時對應的弦在圓內分布卻是不均勻的。P2值時，弦在圓內是隨機分布的。P3值時，弦中點是隨機分布的但此時對應的弦在圓內分布卻是不均勻的。筆者對于貝特朗悖論多解下隨機分布的情況將另行討論，此處集中討論應用無差別原則導致的相關悖論問題。

對于貝特朗悖論的研究，有很多學者從不同角度給出了多種答案，現分析其中一例(圖10)。

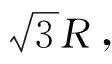
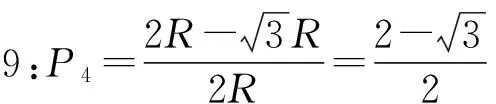
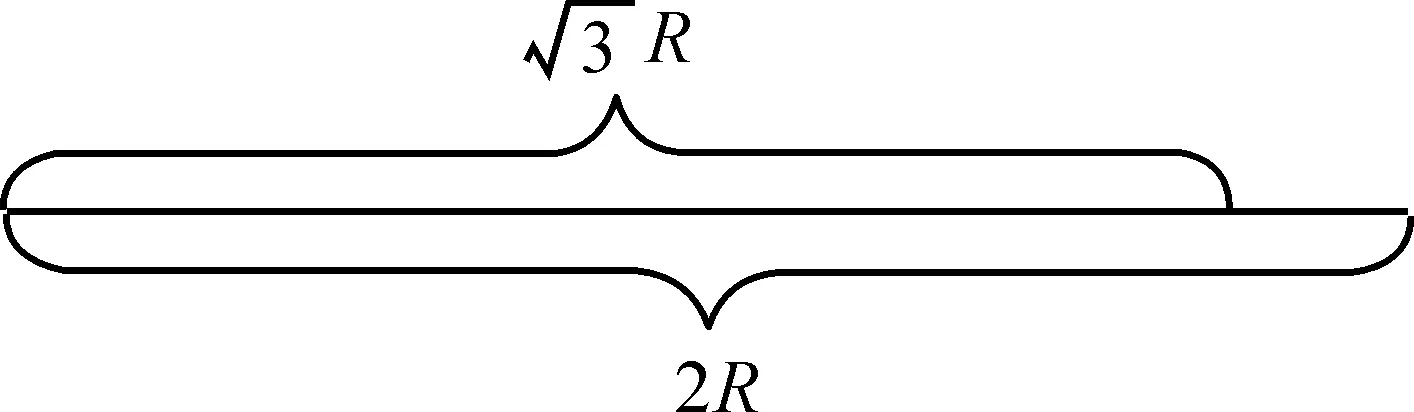
圖10

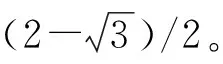
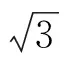
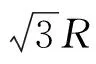
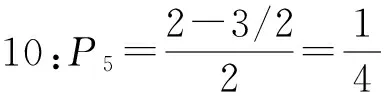
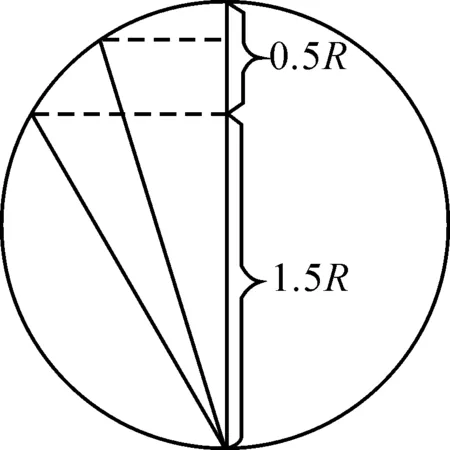
圖11

對于第四種答案提出的多種模型以及第五種答案，均是通過降維，用一維線段長度來計算。這類算法是對問題的過度抽象，這導致對應的實際模型會有無數種情況，所以計算結果已經完全脫離了題目本身在二維坐標下構建模型的含義，再討論是否合理地運用了無差別原則也就顯得沒有意義了。這是完全不同于原有的3種經典解答的，經典的3種解答都正確運用了無差別原則，也都分別從自身角度解釋了自己對隨機弦的理解，雖然答案不一樣，產生了悖論，但每一種答案都對應了一個準確的概率值，可以用實際實驗進行模擬驗證。第一種算法的1/3對應的是：弦的兩個端點在圓周上是隨機無差別分布的“隨機弦”概率值；第二種算法的1/2對應的是：目前學者們普遍認為的弦在圓內隨機無差別分布的隨機弦概率值；第三種算法的1/4對應的是：弦中點在圓內隨機無差別分布的“隨機弦”概率值。雖然產生了悖論，但是學者們爭論的焦點在于何為隨機弦，當隨機弦的定義得到統一和廣泛認可后，悖論自然就會消除。筆者的分析對于無差別原則的重新認識有一定的啟發，可以鞏固使用無差別原則的合理性。

四、結束語

概率的邏輯解釋是以無差別原則作為基本原則來確定初始的概率。對于無差別原則相關的悖論研究有利于鞏固概率邏輯解釋的基礎。本文對無差別原則悖論中的酒水悖論和貝特朗悖論的多解進行分析解讀，詮釋酒水問題是由于在運用無差別原則時沒有前后統一的一個不變的基準而導致的悖論。而貝特朗問題其本質并不是由于錯用無差別原則導致的悖論，而是對原有問題轉化為不同算法時采用了不同的前提假設。對于貝特朗悖論中，無論是經典的3種算法給出的各自對應的隨機分布，還是第四、五種答案中轉化采用的降至一維的解法等，其產生悖論的本質都不應該是對無差別原則的質疑，不論是在這5種算法還是在延伸的更多的算法中，都少不了對原有問題的轉化。將問題轉化確定后，在計算過程中正確運用無差別原則的前提下，還需要確定在同一個前提下的相關量之間如何進行正確的轉化，而不能反復多次對不同的參數濫用無差別原則。貝特朗悖論的解決關鍵在于如何對隨機弦定義進行統一，當弦的隨機選取被統一和廣泛認可后，會避免在轉化過程中誤用或濫用無差別原則等很多問題，悖論也就隨之消失。本文是對這類悖論的剖析，是從結果出發，發現悖論產生的本質原因，并圍繞無差別原則在整個計算過程中的合理性進行分析。本研究對無差別原則的重新認識以及對鞏固概率邏輯解釋的基礎都有一定意義。

參考文獻：

[1]KEYNES J M.A treatise on probability[M].Cambridge ：Cambridge University，Courier Corporation，1921：45.

[2]LAPLACE P S.Essai philosophique sur les probabilités[M].[S.l]:[s.n.],1814:320-340.

[3]顏青山.酒水悖論的幾何化解決[J].科學技術哲學研究，2015(3):1-4.

[4]BERTRAND J.Calcul des probabilités[M].Paris:Gauthier-Villars，1889:4-5.

[5]GARDNER M.The second scientific American book of mathematical puzzles and diversions[M].Chicago:University of Chicago Press,1987:223-226.

[6]陳作清.關于貝特朗奇論的新見解[J].西北民族大學學報(自然科學版)，1998(1):64-65.

[7]JAYNES E T.The well-posed problem[J].Foundations of Physics，1973，3(4):477-492.

[8]陳曉平.無差別悖論及其解決[J].邏輯學研究，2013(1):49-71.

[9]李文明.關于貝特朗悖論的探索與進展[J].中學數學研究 (華南師范大學版),2013(3):47-50.