一類具有預防控制的傳染病模型研究

閆婷婷

（晉中職業技術學院，山西 晉中 030600）

傳染病是人類疾病中不可避免且廣泛存在的一種疾病，因其種類繁多危害性大且情況各異，所以人類對傳染病的研究一直在深入且細化。通過數學模型對傳染病的傳播過程、病齡結構、預防控制進行細化分析研究，做出疾病控制的有效措施。

在辛京奇等文中基于經典的具有常數輸入率和雙線性傳染率的SIR模型，建立一類具有接種的SIR-V傳染病模型，得到了基本再生數，并證明了全局漸近穩定性[1]。楊亞莉等討論了一類具有接種和因病死亡的SIS-V傳染病模型的全局穩定性[2]。本文主要討論一類具有預防接種的傳染病模型，分析其平衡點的類型及無病平衡點和有病平衡點的全局穩定性。

1 模型的建立

如式（1）所示為一種具有預防接種的傳染病模型，

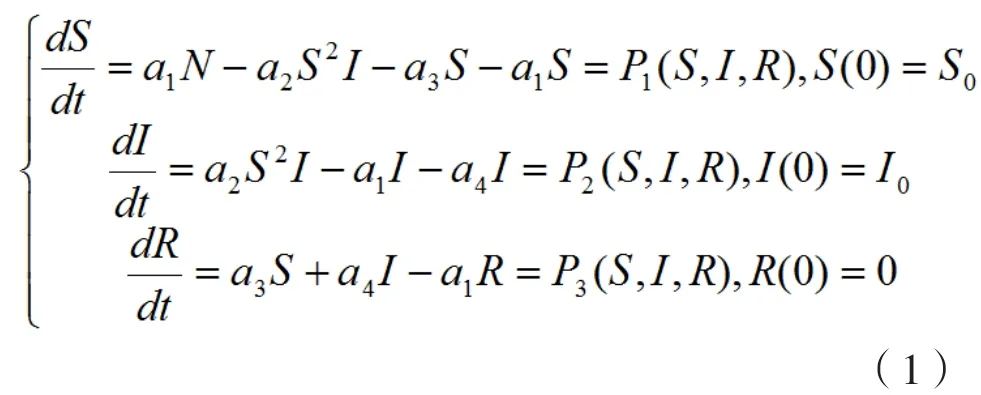
其中S(t)表示t時刻易感染者數量，I(t)表示t時刻染病者數量，R(t)表示t時刻恢復者數量。N =S +I+R 表示總人口數量，a1表示出生率與死亡率的差值，a2表示染病率，a3表示接種率，a4表示恢復率。

引理1常數變量公式

2 系統的平衡點分析

定理1 總人口數量N是不變的。

證明 由于 N =S +I +R ，故有

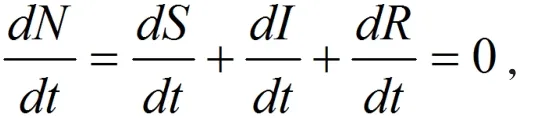
因此N是不變的，即 N= N0。

定理2系統（1）的解是有界的。

證明 因S(t)，I(t)，R(t)均表示人口數量，故S(t)，I(t)，R(t)≥0，又 N =S +I +R，再利用定理1知

系統（1）的平衡點應滿足方程組

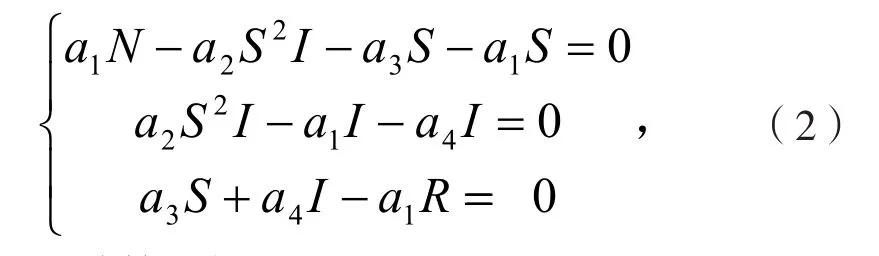
經計算，知（2）有兩個解

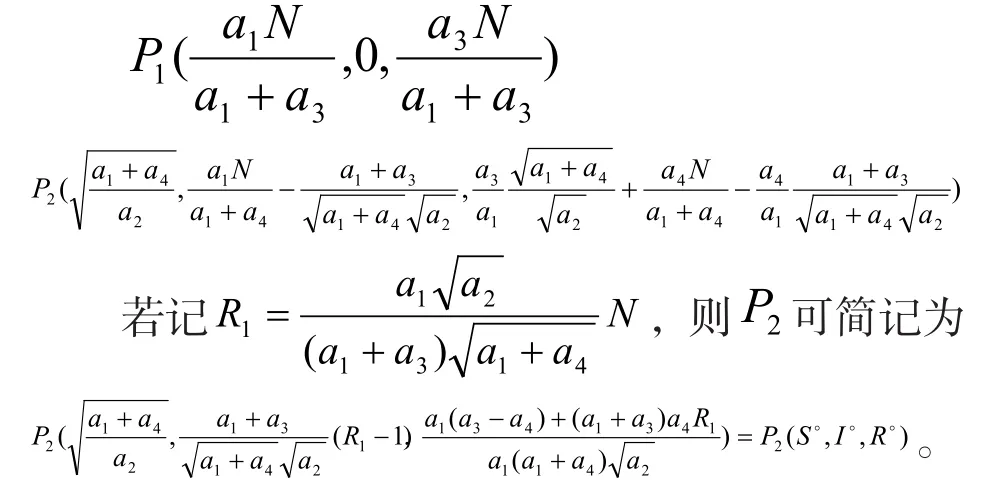
設P(S?,I?,R?)為系統（1）的任意一個平衡點，則（1）在P處的線性近似系統的特征方程為

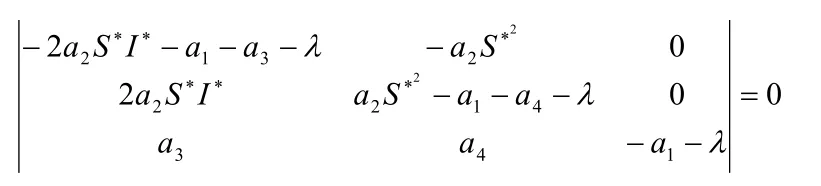
因此系統（1）在1P處的特征方程為：

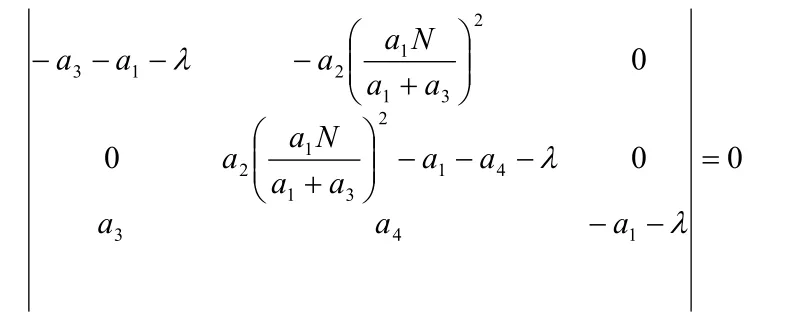
經計算解得

當 R1＜1時， λ2＜0，因此當 R1＜1時，為穩定的平衡點；

當 R1＞1時， λ2＞0，因此，當 R1＞1時，P1為不穩定的平衡點。

當 R1＞1，P2為正的平衡點，符合實際情況，系統（1）在P2點處的特征方程為;

特征根 λ1=-a1＜0，剩下的兩特征根應滿足方程

化簡，得

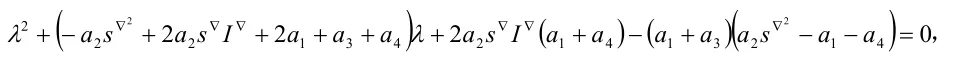
進一步化簡，得

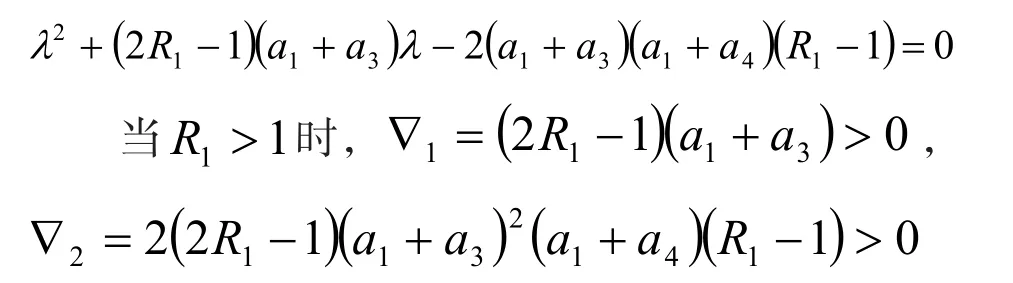
故由引理4知，P2為穩定的平衡點。

定理3 當 R1＜1時，系統（1）的平衡點 P1是穩定的；當 R1＞1時，平衡點 P1是不穩定的，但平衡點P2是穩定的。

3 平衡點的全局穩定性

定理4 當 R1＜1時，系統（1）的平衡點 P1是全局漸近穩定的。

由Bendixson判定知，系統（1）在G內無閉軌，又知當 R1＜1時，在G內只有一個平衡點 P1是穩定的，故 P1點是全局穩定的。

由于（1）中的兩個方程不含R，故也可以考察（1）的前兩個方程構成的子系統：

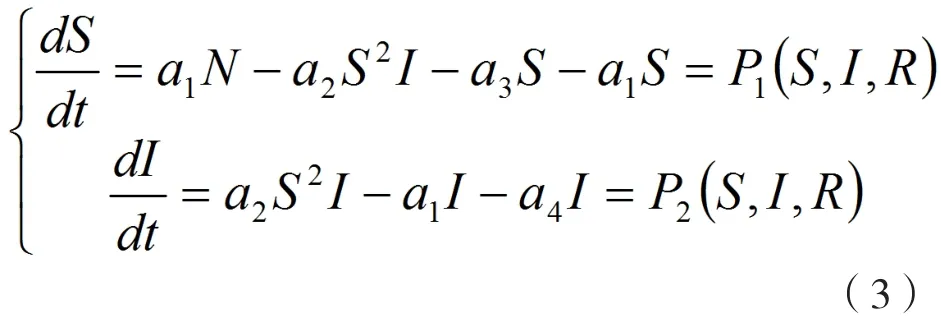
（3）的平衡點應滿足方程組

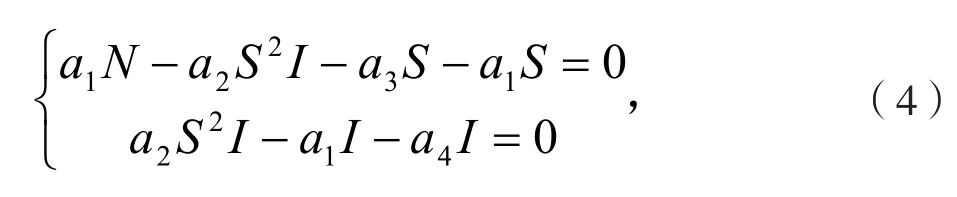
經計算知（4）有兩個解

（3）在 Q (S?,I?)處的線性近似系統的特征方程為

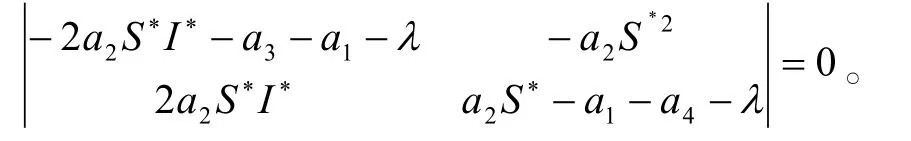
因此（3）在Q1處的特征方程為：

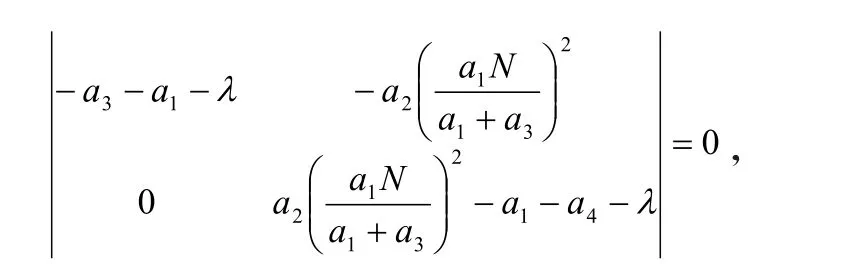
解得 λ1= -(a1+a3)＜ 0，

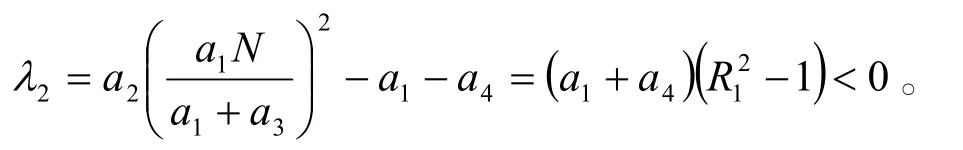
因此可見當 R1＜1時， λ2＜0，因此Q1為穩定的平衡點。當 R1＞1， λ2＞0，Q1為不穩定的平衡點。

系統（3）在Q2處的特征方程為

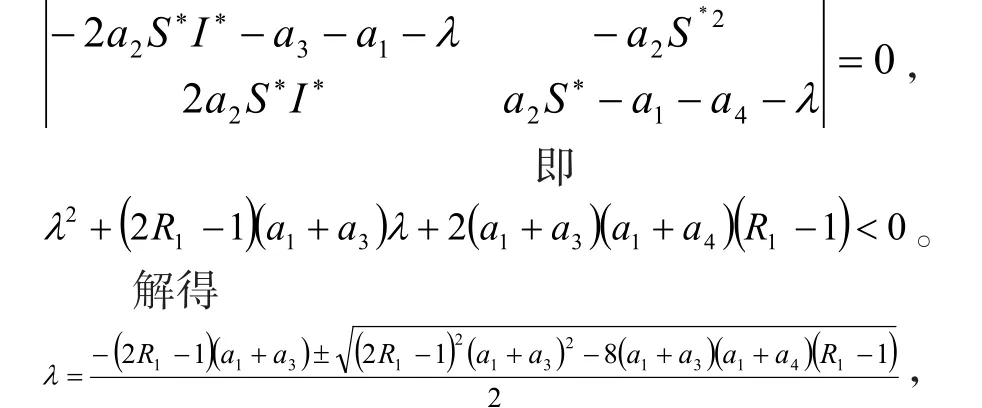
顯然，從上式可以看出，當 R1＜1時，有特征根λ ＜0，故Q2為穩定的平衡點。

即有如下的結論：

定理5 當 R1＜1時，（3）的平衡點Q1是穩定的；當 R1＞1時，Q1是不穩定的，但Q2是穩定的。

定理6 對于系統（1）當 R1＜1時，有

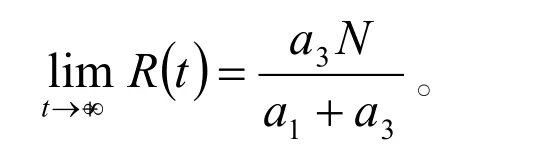
證明 當 R1＜1時，Q1是全局穩定的，因此有

將上式代入系統（1）中，有如下的極限方程

利用常數變量公式解得

又因R(0)=0，故C=0，即

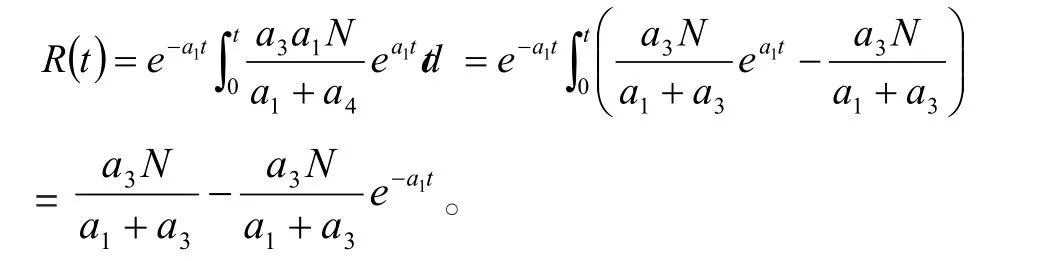
從上述分析可以看出，當 R1＜1時，該傳染病根本不會傳播開來。但 R1＞1時，該傳染病將會流行開來，因此，需要通過降低R1的值來控制。

4 結論

本文主要討論了一類具有預防接種的傳染病模型，利用常數變量公式及Bandixson判定法進行了理論研究，分析了其平衡點類型，得到了無病平衡點和有病平衡點的全局穩定性。當基本再生指數小于1時，該傳染病根本不會傳播開來。但基本再生指數大于1時，該傳染病將會流行開來，因此，需要通過降低R1的值來控制傳染病的流行。

[1] 辛京奇，王文娟.一類帶有接種的SIR傳染病模型的全局分析[J].數學的實踐與認識，2001,(20):71-76.

[2] 楊亞莉，李建全，張吉廣.一類帶有接種的傳染病模型的全局性分析[J].西北大學學報，2009,(5):729-731+749.