基于預(yù)期的報童問題研究
文 平,龐慶華
(1.常州工學(xué)院數(shù)理化工學(xué)院,江蘇 常州 213022; 2.河海大學(xué)企業(yè)管理學(xué)院,江蘇 常州 213022)
1 引言
一個標(biāo)準(zhǔn)的隨機存貨管理模型是單階段報童問題。自從Arrow等[1]開始關(guān)注該問題之時,報童問題得到了來自各領(lǐng)域?qū)W者的廣泛研究。與之同名的故事是這樣講的,早晨報童必須決定從報社訂多少報紙。他所遇到的難題是他并不知道有多少顧客要買他的報紙,假如他訂的報紙?zhí)啵麑⒂锌赡芤驗閳蠹堎u不出去而遭受損失,假如他訂的太少,也有可能失去獲得額外利潤的機會。這種經(jīng)典的單階段存貯問題被稱為報童問題。報童問題在企業(yè)管理中經(jīng)常會碰見,商業(yè)企業(yè)的訂貨量問題,生產(chǎn)企業(yè)的產(chǎn)出量問題都可歸結(jié)為與報童問題,因此對報童問題的研究非常重要[2-3]。
經(jīng)典的報童模型是建立在風(fēng)險中性的假設(shè)基礎(chǔ)之上的,認為報童會選擇一個使期望利潤達到最大的訂貨量。然而,實證表明實際訂貨量往往偏離經(jīng)典報童模型的最優(yōu)訂貨量,而且,大部分實證結(jié)果還表明報童傾向于訂購比經(jīng)典報童模型的最優(yōu)訂貨量少的貨物。為了解釋這種現(xiàn)象,學(xué)者們從不同角度對報童問題進行了研究。Eeckhoudt和Gollier[4]在期望效用理論框架下討論了風(fēng)險厭惡的報童的訂貨量,并對影響訂貨量的各個因素進行了比較靜態(tài)分析,Arikan和Fichtinger[5]也做了類似研究工作。文平[6]則在Kahneman與Tversky[7-9]提出的預(yù)期理論(Prospect Theory)框架下對報童問題進行了討論,他的研究表明訂貨量不僅與價格等因素有關(guān)還與報童的損失厭惡程度有關(guān),并且損失厭惡使得訂貨量比經(jīng)典報童模型的訂貨量少。Gotoh和Takano[10]利用條件在值風(fēng)險討論了報童問題。Wang等[11-12]同樣將損失厭惡運用于報童問題模型中,他發(fā)現(xiàn)假如短缺成本不被忽略,損失厭惡的報童的訂貨量要比經(jīng)典的報童的訂貨量要多。類似的,曹兵兵等[13]針對溫度敏感型的產(chǎn)品研究發(fā)現(xiàn),考慮損失厭惡的報童的訂貨量往往高于經(jīng)典報童中該產(chǎn)品的訂購量。不過Wang和曹兵兵用的效用函數(shù)與文平所用的效用函數(shù)不同,自然所得研究結(jié)果也不相同。Fabian[14]假設(shè)報童是基于預(yù)期的損失厭惡的人,他認為報童的參照點是以往的利潤數(shù)據(jù),在這些假設(shè)下,他推出報童的訂貨量要比經(jīng)典報童模型的訂貨量少。Xu Xinsheng等[15]研究發(fā)現(xiàn)在CVaR環(huán)境下,損失厭惡的報童的訂貨量可能高于也可能低于經(jīng)典報童的訂貨量。Vipin和Amit[16]研究發(fā)現(xiàn)損失厭惡可以顯著改善效用函數(shù)模型在預(yù)測合理行為方面的性能。此外,劉作義和查勇[17],劉詠梅等[18],張艷霞等[19]也在預(yù)期理論框架下對報童問題進行了較深入的討論,周艷菊等[20]則用預(yù)期理論研究了兩產(chǎn)品報童問題。
2006年,Koszegi與Rabin[21-22]提出了參照依賴偏好理論,這是對決策理論的進一步發(fā)展。從前的經(jīng)濟、管理模型絕大部分是在期望效用理論框架下構(gòu)建的。自預(yù)期理論建立以來,部分經(jīng)濟、管理問題則轉(zhuǎn)而用該理論進行討論,報童問題也不例外。正如前文所述,報童問題的討論也經(jīng)過了上述過程。Koszegi與Rabin[21-22]的參照依賴偏好理論被提出后,已經(jīng)開始被用于一些經(jīng)濟、管理問題的研究中,并且得到了一些比較好的結(jié)果。本文就準(zhǔn)備改變了以往的研究模式轉(zhuǎn)而用Koszegi與Rabin[21-22]的參照依賴偏好理論對報童問題進行研究。研究主要集中在下面幾個方面,一是求得報童問題的最優(yōu)訂貨量;二是討論報童問題解的性質(zhì);三是對涉及報童訂貨量的諸要素的進行必要的比較靜態(tài)分析。
2 參照依賴偏好理論
對于無風(fēng)險收入x與參照點r,Koszegi與Rabin[21-22]給出的效用函數(shù)為:u(x)=m(x)+μ(m(x)-m(r))。他們稱m(x)為內(nèi)在的消費效用函數(shù),稱μ(m(x)-m(r))為參照依賴的獲得-損失效用。顯然,如果收入低于參照點,獲得-損失效用為負效用,收入高于參照點的獲得-損失效用才為正效用。Koszegi與Rabin[21-22]進一步將參照依賴的效用擴展至隨機情形。
設(shè)X表示隨機收益,其分布函數(shù)為F(x),又設(shè)Y為隨機參照點,其分布函數(shù)為G(y),Koszegi與Rabin[21-22]給出的參照依賴的效用定義如下。
U(X|Y)=?u(x|y)dG(y)dF(x)
(1)
這里,u(x|y)=m(x)+μ(m(x)-m(y)),其中,m(x)為連續(xù)可導(dǎo)且單調(diào)遞增的消費效用函數(shù),μ(x)為獲得-損失效用函數(shù)。μ(x)滿足下列特點。
A0.μ(x)為二階可導(dǎo)的連續(xù)函數(shù)且μ(0)=0;
A1.μ(x)為嚴(yán)格單調(diào)遞增的;
A2.若y>x>0,則μ(y)+μ(-y)<μ(x)+μ(-x);
A3.當(dāng)x>0時,μ″(x)≤0;當(dāng)x<0時,μ″(x)≥0;
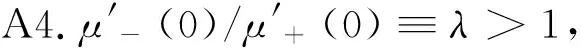
根據(jù)Koszegi和Rabin[21-22]有關(guān)論述,為討論問題方便起見,可以做幾個假設(shè)。首先,m(x)可以被看作是線性的,即m(x)=x;第二,可以用一個分段線性函數(shù)來描述獲得-損失效用函數(shù),即:
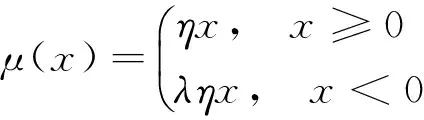
(2)
這里,λ與η為非負常數(shù)。參數(shù)λ表示損失厭惡程度,它控制著決策者關(guān)于損失和獲得的態(tài)度。如果λ等于1,決策者是損失中性的;如果λ大于1,決策者是損失厭惡的;如果λ小于1,決策者是損失偏好的。η表示獲得-損失效用在決策中的重要性,它越大獲得-損失效用在決策中起的作用越大,反之,消費效用在決策中起的作用越大。
3 報童模型
3.1 經(jīng)典報童問題的最優(yōu)解
在報童問題中,報童必須在面對隨機需求的前提下選擇一個訂貨量q。設(shè)X為某一階段的隨機需求,其分布函數(shù)為F(x),其概率密度函數(shù)為f(x)。隨機需求X為一非負的隨機變量,它定義在區(qū)間I=[a,b]上,這里0≤a
g(q,X)=(p-s)min(q,X)-(c-s)q
(3)
分析該問題的傳統(tǒng)方法假設(shè)報童是風(fēng)險中性以及損失中性的決策者,報童以最大化預(yù)期利潤為目標(biāo),報童的期望利潤為:

(4)
預(yù)期利潤對q求導(dǎo)并讓該導(dǎo)數(shù)等于零,從而有:
(p-s)F(q)=p-c
(5)
故最優(yōu)訂貨量q*為:
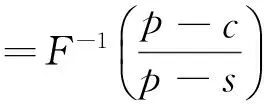
(6)
這就是經(jīng)典報童問題的最優(yōu)解。
3.2 基于預(yù)期的報童模型
根據(jù)Koszegi與Rabin[21-22]的參照依賴偏好理論,報童總的效用由兩部分組成:內(nèi)在的消費效用和獲得-損失效用。內(nèi)在的消費效用等于報童的期望利潤,獲得-損失效用通過利潤與參照點的比較得到。Koszegi與Rabin[21-22]認為報童的參照點由報童關(guān)于利潤的理性預(yù)期決定,也就是說可以選取報童的利潤本身作為報童的參照點,Abeler[24]與Ericson和Fuster[25]支持了理性預(yù)期作為參照點的觀點。這時,報童的效用用Koszegi與Rabin[21-22]的表示方法可以表示為U(g|g)。為討論參照依賴的效用為U(g|g)的具體形式,先介紹一個定義和一個引理,該引理及其證明詳見Koszegi與Rabin[21]。
定義1 設(shè)X的分布函數(shù)為F(x),X到自身的距離S(X)為:
S(X)=?|x-y|dF(x)dF(y)
引理1 假設(shè)消費效用函數(shù)m(x)為線性函數(shù),獲得-損失效用函數(shù)μ(x)為分段線性函數(shù),其函數(shù)形式如(2)式所示。則對于任意收益X,它的參照依賴的效用為:
(7)
在消費效用函數(shù)為線性函數(shù)以及獲得-損失效用函數(shù)為分段線性函數(shù)假設(shè)下,根據(jù)引理1,報童關(guān)于利潤的參照依賴的效用為:
(8)
其中,利潤g的形式如(3)式所示。這時,
為求得參照依賴的效用最大值,U(g|g)對q求一階導(dǎo)數(shù)得到:
U′(g|g)=(p-c)-(p-s)F(q)-η(λ-1)(p-s)F(q)(1-F(q))
(9)
令一階導(dǎo)數(shù)為零得到:
(p-c)-(p-s)F(q)-η(λ-1)(p-s)F(q)(1-F(q))=0
(10)
這就是基于預(yù)期的報童的訂貨量所滿足的條件,特別如果損失厭惡系數(shù)λ=1,報童的訂貨量q為:
(11)
此時,基于預(yù)期的報童的最優(yōu)訂貨量即為經(jīng)典報童問題的最優(yōu)訂貨量。下面討論基于預(yù)期的報童的訂貨量所具有的性質(zhì)。
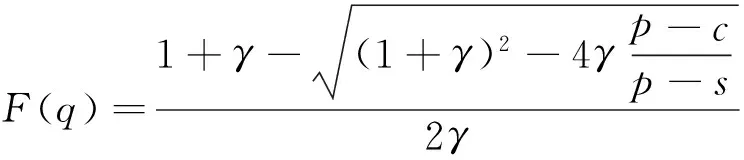
證明:方程(10)可以視為關(guān)于F(q)的一元二次方程,該方程經(jīng)過整理變形得到:
(12)
其求根判別式為:

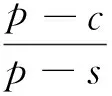
所以,方程(12)總存在實數(shù)解,即基于預(yù)期的報童的最優(yōu)訂貨量存在。
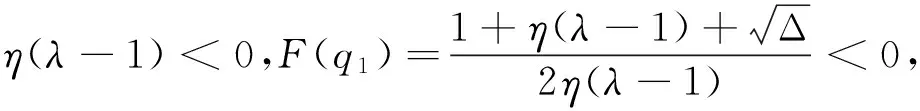
由性質(zhì)1可以看出,以預(yù)期利潤為參照點的報童問題仍然存在唯一的最優(yōu)訂貨量。這就意味著以預(yù)期利潤為參照點的報童問題不但符合決策者的實際決策情況,而且總能找到一個使報童總效用最大化的最有訂貨量。性質(zhì)1同時也表明在實際工作中,如果零售商(報童)具有損失厭惡,其訂購決策是以預(yù)期利潤為參照點,那么其最優(yōu)的訂貨量可以根據(jù)F(q)的表達式進行確定。另外從性質(zhì)1的證明過程可以得到一個副產(chǎn)品,不妨用引理2加以表述。
引理2.無論正數(shù)λ,η取何值,基于預(yù)期的報童的最優(yōu)訂貨量滿足1+η(λ-1)-2η(λ-1)F(q)>0。
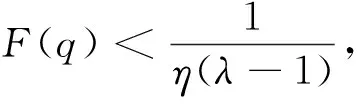
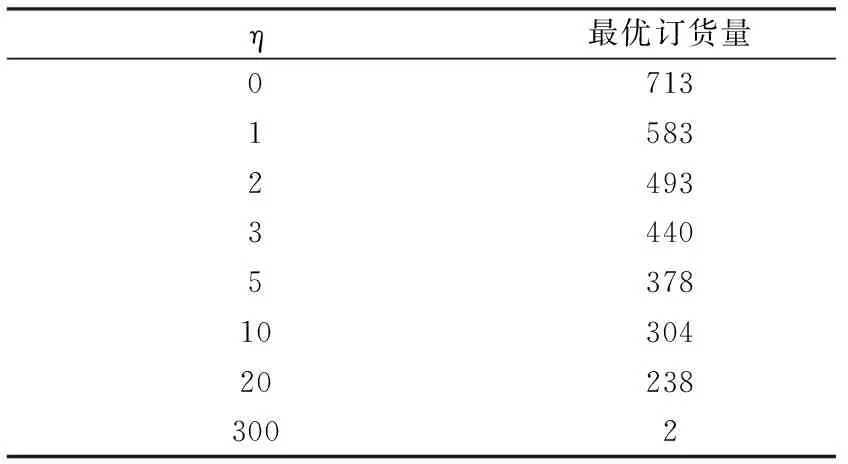
性質(zhì)2. 若λ>1,基于預(yù)期的報童訂貨量嚴(yán)格小于利潤最大化的報童的訂貨量,即q 由引理2知道1+η(λ-1)-2η(λ-1)F(q)>0,故?q/?λ<0。 性質(zhì)2說明當(dāng)報童是損失厭惡的決策者時,基于預(yù)期的報童的訂貨量小于經(jīng)典報童問題的訂貨量,而且隨著損失厭惡系數(shù)λ的增加而減少。損失厭惡系數(shù)λ越大,報童的訂貨量就越小;損失厭惡系數(shù)λ越小,報童的訂貨量就越大。當(dāng)λ趨近于正無窮時,報童的訂貨量趨于貨物銷售量的下限a;當(dāng)λ趨近于1時,報童的訂貨量則趨近經(jīng)典報童問題的訂貨量q*。所以,當(dāng)損失厭惡系數(shù)λ在區(qū)間(1,+∞)內(nèi)變化時,基于預(yù)期的報童的訂貨量則從經(jīng)典報童問題的訂貨量q*逐步減少到貨物銷售量的下限a。這意味隨著報童對損失厭惡程度的提升,如果以預(yù)期利潤為其決策參照點,則損失對其帶來的負效用影響越來越大。在負效用影響下,零售商(報童)為了取得縮小實際利潤與預(yù)期利潤之間的差距,其將逐漸降低自己的訂貨量。 性質(zhì)3.若λ<1,基于預(yù)期的報童訂貨量嚴(yán)格大于利潤最大化的報童的訂貨量,即q>q*。而且?q/?λ<0。 性質(zhì)3說明當(dāng)報童是損失偏好的決策者時,基于預(yù)期的報童的訂貨量大于經(jīng)典報童問題的訂貨量,而且基于預(yù)期的報童的訂貨量隨著損失厭惡系數(shù)λ的增加而減少。性質(zhì)3意味著當(dāng)報童具有損失偏好時,如果以預(yù)期利潤為其決策參照點,此時報童的獲得-損失效用為正效用,其訂貨量越多,帶給自身的正效用越大。在此情形下,基于預(yù)期的報童訂貨量將會大于利潤最大化的報童的訂貨量。從實際問題來看,這說明在零售商(報童)具有損失偏好時,相對于自己的所失,其往往更注重自己的所得,因此其往往會加大訂貨量,這與現(xiàn)實情形是一致的。 性質(zhì)4.基于預(yù)期的報童訂貨量具有下列特點。 (2)當(dāng)γ→+∞時,F(xiàn)(q)→0; (3)當(dāng)γ→-∞時,F(xiàn)(q)→1。 可以利用性質(zhì)1直接得到性質(zhì)2的結(jié)論,這里免證。γ趨近于0,則λ趨近于1或者η趨近于0,說明如果報童是損失中性的或者報童只考慮消費效用,報童的訂貨量趨近于經(jīng)典報童問題的訂貨量。該性質(zhì)的第二條說明極端的損失厭惡的報童或者只考慮獲得-損失效用的報童的訂貨量趨近于貨物銷售量的下限;與之相反,極端的損失喜好的報童的訂貨量趨近于貨物銷售量的上限。 性質(zhì)5. 若λ>1,基于預(yù)期的報童訂貨量嚴(yán)格小于利潤最大化的報童的訂貨量,而且?q/?η<0;若λ<1,基于預(yù)期的報童訂貨量嚴(yán)格大于利潤最大化的報童的訂貨量,而且?q/?η>0。 該性質(zhì)說明如果報童是損失厭惡的,隨著獲得-損失效用在決策中的作用的增加,報童的訂貨量將逐漸減少。反之,如果報童是損失喜好的,隨著獲得-損失效用在決策中的作用的增加,報童的訂貨量將逐漸增加。 性質(zhì)6.設(shè)q為基于預(yù)期的報童在面對隨機需求X的訂貨量,Y=cX+d,Q為基于預(yù)期的報童在面對隨機需求Y的訂貨量。在其他參數(shù)不變的條件下,Q=cq+d。 該性質(zhì)說明如果隨機需求呈線性變化時,基于預(yù)期的報童的訂貨量也呈現(xiàn)相應(yīng)的線性變化。 性質(zhì)7.基于預(yù)期的報童的訂貨量隨價格p的增加而增加,即?q/?p>0。 證明:(12)式兩邊同對p求偏導(dǎo)數(shù)得到: 解之得到: 由引理2知道1+η(λ-1)-2η(λ-1)F(q)>0,所以?q/?p>0。 性質(zhì)7說明貨物的銷售價格越高,報童的訂貨量越大。單位價格p越大,報童的訂貨量越接近于貨物銷售量上限b,這一點從(10)式也可以看出;反之,p越小,報童的訂貨量越小;特別取p=c,根據(jù)(10)式可知F(q)=0,報童的訂貨量等于貨物銷售量的下限a。從性質(zhì)7也可以看出,在報童以預(yù)期利潤為其決策參照點時,隨著銷售價格的增高,訂貨量的增加將進一步提高其獲得-損失的正效用,對于具有損失厭惡的報童來說擴大訂貨量是其最優(yōu)選擇。因此在實際工作中,為了使得具有損失厭惡的報童能夠擴大訂購量,在市場銷售價格難以改變情況下,可以通過降低批發(fā)價格來提高報童的獲得-損失正效用,這也是企業(yè)在生產(chǎn)經(jīng)營中常常用到的策略。 性質(zhì)8.基于預(yù)期的報童的訂貨量隨s的增加而增加,即?q/?s>0。 證明:(12)式兩邊同對s求偏導(dǎo)數(shù)得到: 性質(zhì)8說明報童訂貨量隨s單調(diào)遞增。s越大報童因賣不出去遭受的損失越小,報童的訂貨量自然越大,特別當(dāng)s=c時,顯然方程(12)的解為F(q)=1,即q=b,也就是報童的訂貨量達到貨物銷售量的上限b。性質(zhì)8說明了從產(chǎn)品的殘值與報童訂貨量之間的關(guān)系,因此從另一方面來說,為了使得具有損失厭惡的報童能夠擴大訂購量,在市場銷售價格和批發(fā)價格難以改變情況下,可以通過對報童銷售期末的剩余產(chǎn)品給予一定的補貼,這意味提高了剩余產(chǎn)品的殘值,從而提高報童的獲得-損失正效用,這也是在現(xiàn)實生活中我們常常可以看到生產(chǎn)企業(yè)會對其銷售商給予相應(yīng)補貼,提高銷售商加大訂購量的積極性。 性質(zhì)9.基于預(yù)期的損失厭惡的報童的訂貨量隨c的增加而減少,即?q/?c<0。 證明:(12)式兩邊同對c求偏導(dǎo)數(shù)得到: 這個結(jié)論是顯然的。成本c在s到p之間變化,前面討論過當(dāng)c=s時,報童的訂貨量為貨物的銷售上限b;當(dāng)c=p時,由(12)式可知:F(q)=0,即q=a。所以,當(dāng)成本c從s變到p時,報童訂貨量從b變到a。在報童具有損失厭惡時,成本的增加意味著在同等情形下其利潤將變低,報童以期望利潤為決策參照點時,其獲得-損失效用將變小,故其訂貨量將降低。性質(zhì)9說明,在企業(yè)生產(chǎn)經(jīng)營中,應(yīng)該整合有關(guān)業(yè)務(wù)流程,優(yōu)化資源配置,減少一切不必要的支持,有效降低成本,進而能夠擴大自身利潤。 從上述得到的結(jié)論可以看出,在報童具有損失厭惡時,以其預(yù)期利潤為決策參照點,能夠有效預(yù)測和解釋報童訂購決策行為,從而為企業(yè)的運營管理提供決策支持和理論指導(dǎo)。與文平[6]不同的是,本文是在假定需求為連續(xù)隨機變量情況下進行研究的;Wang等[11-12]和曹兵兵等[13]盡管考慮了報童的損失厭惡,但在設(shè)置報童決策參照點時大都選擇了一個固定數(shù)值,不像本文選擇報童預(yù)期利潤這樣的一個隨機變量,因此這些文獻得到了與本文不同的研究結(jié)論,究其原因是由于效用函數(shù)的不同;在Xu Xinsheng等[15]中,由于對報童損失厭惡的定義不同,且是在CVaR下研究損失厭惡對報童訂貨量的影響,因而得到的結(jié)論與本文存在差異。因此,對照已有研究成果來看,本文的研究參照了依賴偏好理論,特別是選取了報童的預(yù)期利潤作為其決策參照點,在此情形下研究了報童的損失厭惡對其訂貨量的影響,使得對報童問題的研究更加符合現(xiàn)實情況,得到的研究結(jié)論能夠解釋理論研究與現(xiàn)實情況之間出現(xiàn)的偏差,從而利用研究得到的結(jié)論更為有效地指導(dǎo)現(xiàn)實工作。 假設(shè)產(chǎn)品的隨機需求服從均值為600標(biāo)準(zhǔn)差為200的正態(tài)分布,即X~N(600,2002)。假如貨物的單位購入成本為3元,貨物的單位售價為8元,貨物的單位殘值為1元,即p=8,c=3,s=1。由性質(zhì)1可知,基于預(yù)期的報童的最優(yōu)訂貨量除了受單位購入成本、貨物的單位售價、貨物的單位殘值等客觀因素決定外還受損失厭惡程度、獲得-損失效用在決策中的重要性等主觀因素的影響。下面分別討論損失厭惡程度、獲得-損失效用在決策中的重要性這兩個因素對報童的最優(yōu)訂貨量的影響。 為討論損失厭惡程度對報童的最優(yōu)訂貨量的影響,先固定獲得-損失效用在決策中的重要性。通常情況下,人們在決策時既要考慮消費效用函數(shù)又要考慮獲得-損失效用,不妨設(shè)這兩者具有相同的重要性,即η=1,損失厭惡程度依次取1、2、3、5、10、20、50、500時基于預(yù)期的報童的最優(yōu)訂貨量如表1所示。 表1 不同損失厭惡程度下報童的訂貨量 由表1可以看到,隨著損失厭惡程度的提高報童的最優(yōu)訂貨量隨之下降,這與性質(zhì)2的結(jié)論是一致的。 當(dāng)討論獲得-損失效用在決策中的重要性對報童的最優(yōu)訂貨量的影響時,則與前者相反,需要固定損失厭惡程度。不妨假設(shè)損失厭惡程度為2,即λ=2,獲得-損失效用在決策中的重要性依次取0、1、2、3、5、10、20、300時基于預(yù)期的報童的最優(yōu)訂貨量如表2所示。由表2可以看到,隨著獲得-損失效用在決策中的重要性的提高,如果報童是損失厭惡的,報童的最優(yōu)訂貨量也會下降,這與性質(zhì)5的結(jié)論是一致的。但是如果報童是損失喜好的,隨著獲得-損失效用在決策中的重要性的提高,報童的最優(yōu)訂貨量反而會提高。 表2 不同決策權(quán)重下報童的訂貨量 報童問題是現(xiàn)實生活中常見的決策問題,對它的研究討論有助于管理者做出科學(xué)的、有效的決策。本文利用Koszegi與Rabin的參照依賴偏好理論對報童問題進行了研究,不僅求得基于預(yù)期的最優(yōu)訂貨量而且討論了最優(yōu)解的性質(zhì)。研究發(fā)現(xiàn),基于預(yù)期的報童的最優(yōu)訂貨量不僅與貨物銷售的概率分布、價格等因素有關(guān)還與報童的損失厭惡程度有關(guān)。如果報童是損失厭惡的,報童的訂貨量要小于經(jīng)典報童問題的訂貨量,而且其訂貨量隨著損失厭惡系數(shù)λ的增加而減少。如果報童是損失偏好的,報童的訂貨量則大于經(jīng)典報童問題的訂貨量,而當(dāng)報童是損失中性時,報童的最優(yōu)訂貨量即為經(jīng)典報童問題的最優(yōu)訂貨量。這些與先前研究的大部分實證結(jié)果是一致的。需要說明的是,損失厭惡在以前也被用于報童問題的研究中,但報童利潤參照點的選取大都為零利潤或者某一個固定的數(shù)值。本文根據(jù)Koszegi與Rabin的思想,選取報童的預(yù)期作為報童利潤的參照點,將報童利潤的參照點從常數(shù)變?yōu)橐粋€隨機變量,這些都為報童問題的研究提供了新的視野。 對報童問題的研究還可以在以下幾個方面進行一些有意義的探索。一是在報童參照點的選取上,本文是將報童的預(yù)期作為報童利潤的參照點,能否選擇別的參照點以及如何在這些參照點下討論報童問題將是值得去做的工作。二是報童問題顯然與決策理論息息相關(guān),近幾十年來,新的決策理論特別是新的風(fēng)險決策理論不斷出現(xiàn),在新的決策理論下討論報童問題也將是一個有意義的工作。 [1] Arrow K J, Harris T, Marschak J. Optimal inventory policy[J]. Econometrica, 1951, 19(2): 250-272. [2] 陳杰, 唐萍, 高騰. 帶有多元馬氏需求的多產(chǎn)品報童模型[J]. 中國管理科學(xué), 2017, 25(2): 57-67. [3] 張永, 張衛(wèi)國, 徐維軍. 無統(tǒng)計信息假設(shè)下的多階段報童決策[J]. 中國管理科學(xué), 2015, 23(5): 107-116. [4] Eeckhoudt L, Gollier H. The risk-averse (and prudent) newsvendor[J]. Management Science , 1995, 41(1): 786-794. [5] Arikan E, Fichtinger J. The risk-averse newsvendor problem under spectral risk measures: A classification with extensions [J]. European Journal of Operational Research, 2017, 256(1):116-125. [6] 文平. 損失厭惡的報童—預(yù)期理論下的報童問題新解[J]. 中國管理科學(xué), 2005, 13(6):64-68. [7] Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk[J]. Econometrica,1979, 47(5): 263-291. [8] Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty[J].Journal of Risk and Uncertainty ,1992, 23(4): 297-323. [9] Tversky A, Kahneman D. Rational choice and the framing of decisions[J]. Journal of Business, 1986, 35(6):251-278. [10] Gotoh J,Takano Y. Newsvendor solutions via conditional-value-at-risk minimization[J]. European Journal of Operational Research, 2007, 179(9):80-96. [11] Wang C X,Webster S. The loss-averse newsvendor problem[J]. Omega, 2009, 37 (4):93-105. [12] Wang C X,Webster S, Suresh N C. Would a risk-averse newsvendor order less at a higher selling price? [J]. European Journal of Operational Research, 2009, 196(8):544-553. [13] 曹兵兵, 樊治平, 尤天慧, 等. 考慮損失規(guī)避的溫度敏感性產(chǎn)品定價與訂貨聯(lián)合決策[J]. 中國管理科學(xué), 2017, 25(4): 60-69. [14] Fabian H. The expectation-based loss-averse newsvendor [J].Economics Letters, 2013, 120(11):429-432. [15] Xu Xinsheng, Meng Zhiqing, Shen Rui, et al. Optimal decisions for the loss-averse newsvendor problem under CVaR[J]. International Journal of Production Economics, 2015, 164(6): 146-159. [16] Vipin B, Amit R K. Loss aversion and rationality in the newsvendor problem under recourse option [J]. European Journal of Operational Research, 2017, 261(2):563-571. [17] 劉作義,查勇. 行為運營管理:一個正在顯現(xiàn)的研究領(lǐng)域[J]. 管理科學(xué)學(xué)報, 2009,12(4):64-74. [18] 劉詠梅, 彭民, 李立. 基于前景理論的訂貨問題[J]. 系統(tǒng)管理學(xué)報, 2010, 19(5):481-490. [19] 張艷霞, 趙晉, 霍佳震. 基于定常風(fēng)險的報童問題風(fēng)險分析. 中國管理科學(xué), 2013, 21(S): 485-494. [20] 周艷菊, 應(yīng)仁仁, 陳曉紅. 基于前景理論的兩產(chǎn)品報童問題研究[J]. 管理科學(xué)學(xué)報, 2013, 16(11): 17-30. [21] K?szegi B, Rabin M. Reference-dependent risk attitudes[J]. American Economic Review, 2007, 97(10): 1047-1073. [22] K?szegi B, Rabin M. A model of reference-dependent preferences[J]. Quarterly Journal of Economics, 2006, 121(7):1133-1165. [23] Sprenger C. An endowment effect for risk: Experimental tests of stochastic reference points[J]. Journal of Political Economy, 2015, 123(6):1456-1499. [24] Abeler J A. Reference points and effort provision[J]. The American Economic Review, 2011, 101(2): 470-492. [25] Ericson K M, Fuster A. Expectations as endowments: Evidence on reference-dependent preferences from exchange and valuation experiments[J].The Quarterly Journal of Economics,2011,126(4): 1879-1907.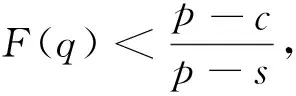
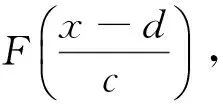
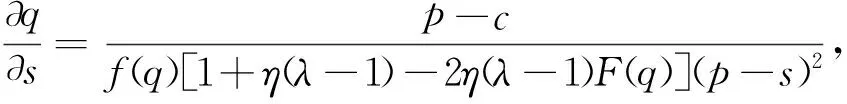

4 算例分析

5 結(jié)語

