高中數(shù)學(xué)中的平面向量數(shù)量積概念分析

王洋洋

（北京師范大學(xué)〈珠海〉附屬高級中學(xué)，廣東 珠海）

高中數(shù)學(xué)平面向量數(shù)量積模塊知識的學(xué)習(xí)見于必修四教材中，在此之前，物理學(xué)科教學(xué)中已經(jīng)接觸了平面向量的概念，有關(guān)數(shù)學(xué)平面向量的學(xué)習(xí)更為理論化、系統(tǒng)化，因此掌握平面向量數(shù)量積概念以解決實際數(shù)學(xué)問題成為教學(xué)重點，這就需要數(shù)學(xué)教師提出有效應(yīng)用策略，從本質(zhì)上來剖析平面向量數(shù)量積概念中的三種形式和相互之間的關(guān)系。

一、重視運算，理解向量本質(zhì)

數(shù)量積是向量的一種運算，而運算的法則就蘊含在平面向量數(shù)量積中，涉及數(shù)量積的定義、幾何含義、坐標(biāo)運算等形式，想要從本質(zhì)上解決平面向量數(shù)量積問題，就要對概念中包含的各種指示加以深化。向量屬于大小和方向同時俱存的量，是矢量，這一特征的掌控是概念理解的基礎(chǔ)。高中教材中給出的平面向量數(shù)量積定義為：兩個向量a，b，夾角為θ，那么|a||b|cosθ叫作a和b的數(shù)量積。表面定義看起來比較簡單，但是想要學(xué)生充分理解這一概念，并且做到靈活運用具有一定的難度，這需要教師在實際解決問題時重視向量運算的講解，以便引導(dǎo)學(xué)生正確把握向量計算中的規(guī)律，夯實向量基礎(chǔ)功底，以便為解決更為復(fù)雜的向量數(shù)量積問題打下堅實的基礎(chǔ)。因此教師可以從以下例題為切入點，為學(xué)生展示出向量知識的活用。

例1：有兩個相互垂直的單位向量m，n，滿足關(guān)系式a-b=-8m+16n，a+b=2m-8n，求出 a·b。

根據(jù)題目給出的條件，明白該題目的目的是幫助學(xué)生理解單位向量，并且對向量進行簡單運算，首先利用單位向量m和n，可以將兩個向量a和b分別求出，化簡a=-3m+4n，b=5m-12n，因此可以得出 a·b=（-3m+4n）（5m-12n）=-63。以上例題屬于基礎(chǔ)的向量知識，可以根據(jù)學(xué)生掌握知識情況適當(dāng)提高題目難度，以進一步提升向量深度。

二、利用圖形，掌握向量

高中數(shù)學(xué)分析平面向量數(shù)量積概念時，不能僅僅局限于單純講解向量定義和客觀規(guī)律有關(guān)的知識點，還應(yīng)該學(xué)會利用圖形，有時能發(fā)揮意想不到的效果，讓學(xué)生更加全面系統(tǒng)地理解向量知識在實踐中的應(yīng)用。

例2：已知三角形ABC中（如下圖所示），AB和AD相互垂直，而且求出向量的值。

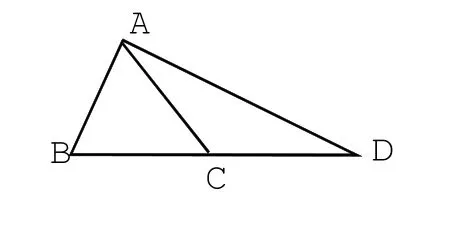
平面向量和三角函數(shù)相結(jié)合的題目是高考中的難點和重點內(nèi)容，想要順利解決此類題目，學(xué)生就必須熟練各種向量的運算技巧，而且還要對三角函數(shù)的多種形式轉(zhuǎn)換完全掌握。根據(jù)題目數(shù)形結(jié)合思想，列出以下演算過程這種根據(jù)圖形來做出向量夾角cosθ可以聯(lián)系三角函數(shù)中角的轉(zhuǎn)化，需要學(xué)生耐心、細(xì)心和用心，觀察圖形更加明確向量的方向指示。

三、通過坐標(biāo)，積極探索

利用坐標(biāo)來解決問題是由參考的圖形的幾何性質(zhì)決定的，建立坐標(biāo)系能夠準(zhǔn)確使用坐標(biāo)表示向量。根本難點在于坐標(biāo)系的建立需要準(zhǔn)確，箭頭方向要具體。從此進入平面向量數(shù)量積概念的學(xué)習(xí)中，兩個數(shù)值之間相乘必然會得到數(shù)值，然而多數(shù)學(xué)生在平面向量數(shù)量積的概念中容易和平面向量相混合，存在誤區(qū)的學(xué)生會將數(shù)量積概念認(rèn)為是兩個向量的相乘也應(yīng)該是向量，而不會在公式中得出大小和方向，由于兩個向量的模和兩個向量之間的夾角的余弦值相乘，最后得到的是數(shù)，因此這種情況才是數(shù)量積而并非向量。少數(shù)學(xué)生對于數(shù)量積和向量兩者之間的混合歸根結(jié)底是對數(shù)量積認(rèn)識不到位，概念理解不夠徹底，從而缺乏應(yīng)用意識和應(yīng)用能力，對此首先要讓學(xué)生在理解概念的基礎(chǔ)上多加訓(xùn)練題目，這是對數(shù)學(xué)中基本概念和定義的掌握，需要注意的是平面向量數(shù)量積是數(shù)不是向量，根據(jù)字面理解最后的乘積必然是數(shù)而并非其他形式。

綜上所述，平面向量數(shù)量積系統(tǒng)概念主要包括定義、幾何意義和坐標(biāo)運算等多個層面。通過概念的應(yīng)用可以理解為數(shù)量積是一個系統(tǒng)才能，學(xué)生在分析概念的基礎(chǔ)上最終形成的結(jié)果必然是要掌握本質(zhì)知識，靈活運用各種概念解決存在的問題。因此作為高中數(shù)學(xué)教師，需要注重概念的分析教學(xué)，并且通過概念分解讓學(xué)生提高認(rèn)識，從而提高數(shù)學(xué)學(xué)科文化素養(yǎng)，和形成改革下高考要求相符合，同時促進數(shù)學(xué)學(xué)科的完善。