基于VW-PCA的盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)故障診斷

郝用興， 劉玉洋,*， 周建軍， 周 洋， 鄭淑娟， 雷 超

(1. 華北水利水電大學(xué)機(jī)械學(xué)院， 河南 鄭州 450045; 2. 盾構(gòu)及掘進(jìn)技術(shù)國家重點(diǎn)實(shí)驗(yàn)室， 河南 鄭州 450001)

0 引言

盾構(gòu)是一種集機(jī)械、電子、液壓等學(xué)科高度融合的大型工程裝備，液壓系統(tǒng)是盾構(gòu)的主動(dòng)力系統(tǒng)。由于現(xiàn)場(chǎng)地質(zhì)條件復(fù)雜，使得液壓設(shè)備性能不穩(wěn)定，沖擊振動(dòng)造成的裝配精度下降、密封件與其配件相互磨損、油液污染、液壓油黏度下降等問題導(dǎo)致液壓系統(tǒng)故障頻發(fā)，帶來嚴(yán)重后果[1]。為確保盾構(gòu)掘進(jìn)過程中安全可靠地運(yùn)行，及時(shí)消除故障隱患，需要對(duì)其進(jìn)行及時(shí)有效的故障診斷。

在盾構(gòu)液壓系統(tǒng)的故障診斷研究方面，文獻(xiàn)[2]將Fisher判別模型應(yīng)用到液壓系統(tǒng)的故障診斷中，證實(shí)了該判別法的實(shí)用性。文獻(xiàn)[3]提出將改進(jìn)的Elman神經(jīng)網(wǎng)絡(luò)算法應(yīng)用于盾構(gòu)故障預(yù)測(cè)系統(tǒng)，并通過工程實(shí)例數(shù)據(jù)驗(yàn)證了該算法的可行性。文獻(xiàn)[4-6]提出將主元分析(PCA)引入到盾構(gòu)液壓系統(tǒng)的故障診斷中，并闡述了其具體應(yīng)用。文獻(xiàn)[7-8]也驗(yàn)證了主元分析模型(PCA)應(yīng)用在故障診斷領(lǐng)域的有效性。傳統(tǒng)診斷模型認(rèn)為每個(gè)系統(tǒng)變量對(duì)于構(gòu)建算法模型有著同樣的作用，這使得各系統(tǒng)變量有著相同的權(quán)值，導(dǎo)致算法模型受到大量無關(guān)信息的影響，增加了從采集信息中獲取故障分類信息的困難程度，無法滿足盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)故障診斷的正確性要求。因此，本文采用變量加權(quán)(VW)算法優(yōu)化傳統(tǒng)主元分析(PCA)模型，并將變量加權(quán)主元分析模型(VW-PCA)引入到盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)的故障診斷中，從而突出主元分析模型(PCA)中各數(shù)據(jù)變量對(duì)不同故障類型的貢獻(xiàn)程度，提高PCA故障診斷的性能。以天津軌道交通φ6 450 mm土壓平衡盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)作為研究對(duì)象，通過AMESim軟件仿真刀盤液壓驅(qū)動(dòng)系統(tǒng)模型及6類故障特征，確定VW-PCA算法模型，獲得各類故障檢測(cè)數(shù)據(jù)的權(quán)值向量，利用已知正常檢測(cè)數(shù)據(jù)構(gòu)建的PCA模型確定控制閾值判斷系統(tǒng)是否發(fā)生故障，再用測(cè)試樣本加以驗(yàn)證VW-PCA算法模型的故障診斷正確性。

1 VW-PCA算法

1.1 VW算法

通常容易提取系統(tǒng)正常運(yùn)行狀態(tài)下各個(gè)變量的監(jiān)測(cè)數(shù)據(jù)，當(dāng)運(yùn)行過程中某一時(shí)刻系統(tǒng)監(jiān)測(cè)值超過控制閾值時(shí)，判斷系統(tǒng)出現(xiàn)故障。此時(shí)通過對(duì)系統(tǒng)各變量賦予不同權(quán)值向量就能夠突顯各個(gè)變量對(duì)故障的影響程度，也可明顯區(qū)別不同種類故障的特征。變量加權(quán)方法有多種，基于SPE和Hotelling’sT2統(tǒng)計(jì)量的貢獻(xiàn)圖就是一種使用廣泛的變量加權(quán)方法。盡管貢獻(xiàn)圖計(jì)算簡(jiǎn)單，但是仍然需要先驗(yàn)知識(shí)來解釋獲得的貢獻(xiàn)圖[9]。文獻(xiàn)[10]指出在變量加權(quán)的數(shù)學(xué)算法中，偏F值是一種較好的加權(quán)方法。偏F值是通過完全借鑒正常運(yùn)行數(shù)據(jù)求得任意故障的權(quán)值向量，也可看作是將正常數(shù)據(jù)樣本與故障數(shù)據(jù)樣本如何分類的問題。令D0∈Rn0×m，Dk∈Rnk×m,其中：k=1,2,…,c;k代表某故障樣本數(shù)據(jù)或正常樣本數(shù)據(jù)；c表示故障種類個(gè)數(shù)總和。對(duì)于任意系統(tǒng)變量xi，其偏F值就是表征數(shù)據(jù)樣本中添入這一變量對(duì)于精確區(qū)分正常數(shù)據(jù)與故障數(shù)據(jù)的貢獻(xiàn)程度。其定義為：

(1)

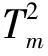
(2)

式中：b0、bk分別為正常類數(shù)據(jù)D0∈Rn0×m和故障類數(shù)據(jù)Dk∈Rnk×m的均值向量；Dk是組合矩陣D0DkT的協(xié)方差陣。

(3)

1.2 VW在主元分析(PCA)上的應(yīng)用

設(shè)采集n次過程數(shù)據(jù)，對(duì)每次采集數(shù)據(jù)都有m個(gè)采集點(diǎn)(變量)，依次用X1,X2,…,Xm表達(dá)，得到初始的資料數(shù)據(jù)矩陣：

X=X1X2…Xmn×m。

(4)

主元分析方法是將討論這m個(gè)變量對(duì)反映整個(gè)系統(tǒng)狀態(tài)信息的問題變?yōu)閷ふ襪個(gè)變量之間存在的線性關(guān)系問題，得到相互獨(dú)立新的組合變量F1,F2,…,Fk(k≤m)，能充分體現(xiàn)原變量所包含的信息。主元分析常規(guī)處理是對(duì)X作正交變換，得到原變量間的線性組合

(5)

滿足每個(gè)主元的系數(shù)平方和為1，即

(6)

主元之間相互獨(dú)立，即無重疊的信息。所以

cov(Fi,Fj)=0i≠j；i,j=1,2,…,m。

(7)

主元間的方差逐次減小，重要程度逐次降低，即

Var(F1)≥Var(F2)≥…≥Var(Fm)。

(8)

由以上各條件得到綜合變量F1，F(xiàn)2，…，F(xiàn)m依次為初始變量的第1,2,…,m個(gè)主元，且每一主元在總體方差中的占比逐次減小。而在現(xiàn)實(shí)應(yīng)用研究中，常選用式(8)中方差較大的前p個(gè)組合變量代替原m個(gè)系統(tǒng)變量，實(shí)現(xiàn)降維的功能。

本文基于刀盤液壓系統(tǒng)，構(gòu)建VW-PCA數(shù)學(xué)模型，故障診斷的基本模型見圖1。

圖1 基于VW-PCA的故障檢測(cè)流程Fig. 1 Flowchart of fault diagnosis based on VW-PCA

為實(shí)現(xiàn)盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)故障診斷，需要將原始已知正常數(shù)據(jù)樣本進(jìn)行主元分析，得到正常數(shù)據(jù)類的Hotelling’sT2的控制限(閾值)，同時(shí)將正常數(shù)據(jù)類與已知各故障數(shù)據(jù)類組合處理得到每一類故障的加權(quán)向量，用各故障類的權(quán)值向量去處理測(cè)試故障樣本數(shù)據(jù)，得到測(cè)試數(shù)據(jù)類的Hotelling’sT2的值，根據(jù)該值判斷測(cè)試數(shù)據(jù)是否發(fā)生故障。

2 變量加權(quán)主元分析(VW-PCA)診斷步驟

2.1 建立已知正常數(shù)據(jù)類的PCA模型

(9)

(10)

(11)

3)利用Q貢獻(xiàn)圖法獲得主元的數(shù)量和相應(yīng)的特征向量。

(12)

在工程應(yīng)用中，以累積貢獻(xiàn)率≥85%選取主元個(gè)數(shù)，即認(rèn)為這些主元素可以體現(xiàn)全部的系統(tǒng)運(yùn)行狀態(tài)。

4)計(jì)算出正常數(shù)據(jù)類的Hotelling’sT2的控制限(閾值)。

(13)

式中Λ為按λ1>λ2>…>λm順序排列的對(duì)角陣。

2.2 建立測(cè)試數(shù)據(jù)類的PCA模型

(14)

利用已求得的特征向量帶入加權(quán)處理后的測(cè)試故障數(shù)據(jù)得到新的主元

(15)

2)算出測(cè)試數(shù)據(jù)類的Hotelling’sT2數(shù)值與2.1節(jié)確定的控制限比較，確定系統(tǒng)是否發(fā)生故障。

3 盾構(gòu)刀盤液壓驅(qū)動(dòng)系統(tǒng)仿真分析

3.1 液壓系統(tǒng)仿真建模

液壓系統(tǒng)是盾構(gòu)工作時(shí)的主動(dòng)力系統(tǒng)，按照盾構(gòu)運(yùn)轉(zhuǎn)時(shí)液壓系統(tǒng)各部分功能不同，可將液壓系統(tǒng)分為刀盤驅(qū)動(dòng)、盾構(gòu)推進(jìn)、管片拼裝機(jī)、螺旋輸送系統(tǒng)等多個(gè)子液壓系統(tǒng)[12]。不同的盾構(gòu)子液壓系統(tǒng)對(duì)應(yīng)著不同的液壓元件組成和控制方式，但是各個(gè)子系統(tǒng)均由基本液壓系統(tǒng)組成，包含了液壓泵、換向閥、液壓缸或液壓馬達(dá)等基本液壓元件。

本文以天津軌道交通φ6 450 mm土壓平衡盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)為研究對(duì)象，針對(duì)刀盤驅(qū)動(dòng)液壓系統(tǒng)故障發(fā)生的特征機(jī)制，研究基本液壓系統(tǒng)的故障診斷方法，然后應(yīng)用到盾構(gòu)液壓系統(tǒng)的各個(gè)子系統(tǒng)的故障診斷中。盾構(gòu)刀盤驅(qū)動(dòng)系統(tǒng)是盾構(gòu)的重要組成部分，承擔(dān)驅(qū)動(dòng)刀盤旋轉(zhuǎn)切削開挖面土體以及攪拌密封艙內(nèi)土體的任務(wù)，具有功率大、功率變化范圍寬、結(jié)構(gòu)復(fù)雜等特點(diǎn)[13]。由于盾構(gòu)刀盤是由多組液壓馬達(dá)驅(qū)動(dòng)組成，而每組馬達(dá)實(shí)現(xiàn)的功能和液壓驅(qū)動(dòng)回路的結(jié)構(gòu)特點(diǎn)基本相同，因此為了便于液壓系統(tǒng)模擬仿真，減少仿真工作量[14]，將所選液壓系統(tǒng)進(jìn)行簡(jiǎn)化，僅選取1組液壓馬達(dá)驅(qū)動(dòng)液壓回路仿真，如圖2所示。系統(tǒng)的工作原理如下： 液壓泵提供動(dòng)力，壓力油經(jīng)過三位四通電磁換向閥進(jìn)入雙向液壓馬達(dá)，驅(qū)動(dòng)馬達(dá)旋轉(zhuǎn)，經(jīng)過齒輪減速器驅(qū)動(dòng)盾構(gòu)刀盤轉(zhuǎn)動(dòng)完成土體的切削，溢流閥控制驅(qū)動(dòng)過程中的系統(tǒng)壓力。采用轉(zhuǎn)動(dòng)負(fù)載模型和轉(zhuǎn)動(dòng)摩擦轉(zhuǎn)矩模型來模擬盾構(gòu)刀盤旋轉(zhuǎn)掘進(jìn)過程中所受到的阻力[15]。

圖2 盾構(gòu)刀盤液壓驅(qū)動(dòng)系統(tǒng)簡(jiǎn)化圖

Fig. 2 Simplified diagram of hydraulic driving system of shield cutterhead

以圖2為仿真對(duì)象，采用AMESim軟件建立盾構(gòu)刀盤驅(qū)動(dòng)系統(tǒng)仿真模型，通過修改關(guān)鍵參數(shù)仿真液壓系統(tǒng)故障。主要仿真參數(shù)設(shè)置見表1。

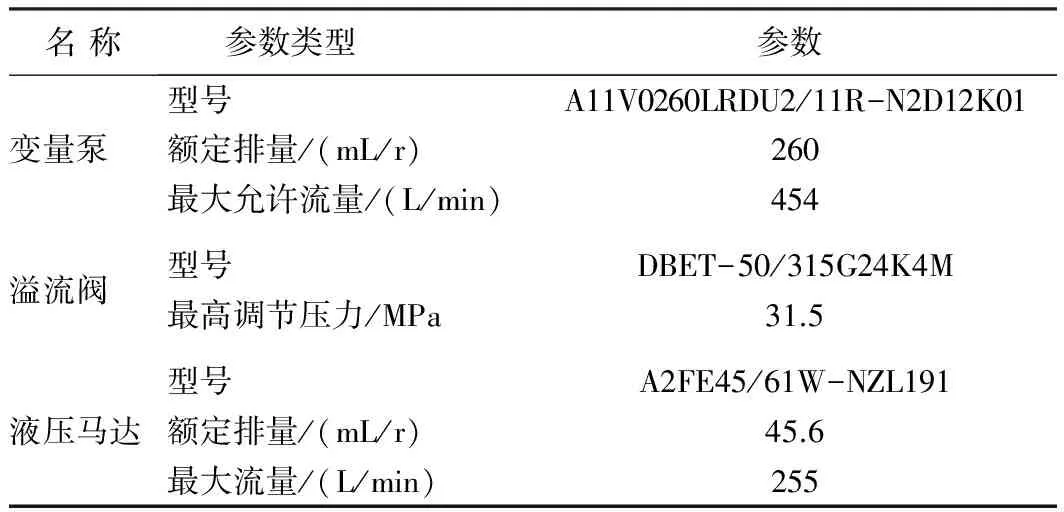
表1 仿真參數(shù)Table 1 Simulation parameters

3.2 故障仿真

本文以刀盤驅(qū)動(dòng)系統(tǒng)作為多變量統(tǒng)計(jì)的故障診斷對(duì)象，其中有壓力、流量、振動(dòng)、溫度、馬達(dá)轉(zhuǎn)速、刀盤轉(zhuǎn)速和摩擦轉(zhuǎn)矩等物理量顯示刀盤驅(qū)動(dòng)系統(tǒng)的運(yùn)行狀況。在圖2所示的液壓回路簡(jiǎn)圖中，AMESim仿真軟件可以直接檢測(cè)到液壓泵工作壓力、液壓泵實(shí)際流量、溢流閥進(jìn)口壓力、液壓馬達(dá)出口壓力、刀盤轉(zhuǎn)速、轉(zhuǎn)動(dòng)摩擦轉(zhuǎn)矩和轉(zhuǎn)動(dòng)負(fù)載轉(zhuǎn)矩等12個(gè)檢測(cè)變量的實(shí)時(shí)值，檢測(cè)變量名稱如表2所示。

表2 檢測(cè)變量Table 2 Diagnosis variables

液壓系統(tǒng)因其各部分液壓元件內(nèi)部結(jié)構(gòu)構(gòu)造復(fù)雜和各回路間耦合作用，使得系統(tǒng)故障產(chǎn)生的準(zhǔn)確位置難以檢測(cè)。但大多故障是由于沖擊振動(dòng)造成的裝配精度下降、密封件與其配件的相互磨損、油液污染、液壓油黏度下降等引起的泄漏故障。同時(shí)，溫升過高導(dǎo)致油液黏度下降及換向閥電磁鐵故障在隧道盾構(gòu)施工過程中也較為常見。因此，在實(shí)際的地鐵施工過程中，盾構(gòu)液壓系統(tǒng)的故障類型繁多，為減少故障仿真的工作量，僅選取液壓泵內(nèi)泄漏、由系統(tǒng)溫升導(dǎo)致的液壓油液黏度下降、換向閥電磁鐵失效等6種故障特征進(jìn)行研究，故障名稱及仿真參數(shù)如表3所示。

表3 故障描述Table 3 Fault descriptions

仿真實(shí)驗(yàn)采取閉環(huán)控制，采樣間隔為10 s，采集1類正常樣本(D0)和6類故障樣本(D1、D2、D3、D4、D5、D6)，每一類樣本個(gè)數(shù)均為800。在MATLAB R2014b軟件環(huán)境下將數(shù)據(jù)導(dǎo)入故障診斷算法模型中，將800組正常數(shù)據(jù)樣本(D0)中的后250組數(shù)據(jù)作為正常類的測(cè)試數(shù)據(jù)，再從6類故障樣本(共4 800組)中隨機(jī)選取150組作為故障類的測(cè)試數(shù)據(jù)，共同組成測(cè)試數(shù)據(jù)集(共400組)。同時(shí)，將剩余正常數(shù)據(jù)樣本(共550組)和剩余6類故障樣本(共4 650組)作為訓(xùn)練數(shù)據(jù)集(共5 200組)，計(jì)算出每一類故障對(duì)應(yīng)各變量的加權(quán)向量，同時(shí)得出正常數(shù)據(jù)類的主元模型。

3.3 仿真結(jié)果與分析

將400組測(cè)試數(shù)據(jù)集分別用傳統(tǒng)PCA算法和變量加權(quán)主元分析算法(VW-PCA)進(jìn)行處理。結(jié)果如圖3所示。

(a) 傳統(tǒng)PCA算法

(b) VW-PCA算法

從圖3中可以看出： 采用傳統(tǒng)PCA算法，前250組正常類的測(cè)試數(shù)據(jù)均未超過閾值，但150組故障測(cè)試數(shù)據(jù)中僅有少量超過閾值，與預(yù)期檢測(cè)效果差距較大，在實(shí)際應(yīng)用中容易出現(xiàn)漏報(bào)； 而采用同樣的測(cè)試數(shù)據(jù)，用1.1節(jié)中變量加權(quán)(VW)的方法處理150組故障測(cè)試數(shù)據(jù)，與傳統(tǒng)PCA算法測(cè)試結(jié)果相比較，易知150組故障數(shù)據(jù)基本都在控制線(閾值)以上，診斷結(jié)果準(zhǔn)確率非常高。

為直觀比較傳統(tǒng)PCA算法與VW-PCA算法在盾構(gòu)刀盤液壓驅(qū)動(dòng)系統(tǒng)故障診斷中的準(zhǔn)確率，分別統(tǒng)計(jì)6類故障數(shù)據(jù)在2種不同算法模型下的準(zhǔn)確率，統(tǒng)計(jì)結(jié)果如表4所示。

表4 VW-PCA與PCA算法故障診斷準(zhǔn)確率對(duì)比

Table 4 Comparison of fault diagnosis accuracy between PCA algorithm and VW-PCA algorithm %

故障類型PCA診斷準(zhǔn)確率VW-PCA診斷準(zhǔn)確率D15993D27995D36489D46690D55791D67294

從表3可以很直觀地看出，假設(shè)各個(gè)系統(tǒng)變量對(duì)于構(gòu)建PCA模型有相同權(quán)重時(shí)，系統(tǒng)診斷正確率低，然而變量加權(quán)主元模型VW-PCA能夠顯著提高系統(tǒng)診斷的正確率，最大可提高50%以上。同時(shí)變量加權(quán)(VW) 能夠增強(qiáng)各系統(tǒng)變量對(duì)不同故障類型的貢獻(xiàn)程度，減少故障信號(hào)的漏報(bào)，提高液壓系統(tǒng)的故障診斷性能。因此，VW-PCA法能夠有效適用于刀盤驅(qū)動(dòng)液壓系統(tǒng)故障診斷。

4 結(jié)論與討論

對(duì)盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)故障及時(shí)有效的診斷是保障盾構(gòu)掘進(jìn)過程安全可靠運(yùn)行的重要環(huán)節(jié)。以天津軌道交通φ6 450 mm土壓平衡盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)作為仿真實(shí)驗(yàn)?zāi)Ｐ瓦M(jìn)行研究，結(jié)果表明： 在盾構(gòu)液壓系統(tǒng)診斷方面，變量加權(quán)主元分析模型(VW-PCA)相比于傳統(tǒng)的主元分析模型(PCA)具有更高的準(zhǔn)確率，診斷效果更佳。

將變量加權(quán)與主元分析算法模型結(jié)合起來，能夠成功實(shí)現(xiàn)盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)的故障診斷，降低故障的漏報(bào)率。但VW-PCA診斷模型僅能判斷出液壓系統(tǒng)是否發(fā)生故障，而無法判斷出液壓系統(tǒng)的具體故障類型。為完善盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)故障診斷方法的研究理論，應(yīng)在此基礎(chǔ)上進(jìn)一步研究液壓系統(tǒng)故障類型的識(shí)別方法。

[1] 劉保杰, 楊清文, 吳翔. 液壓系統(tǒng)故障診斷技術(shù)研究現(xiàn)狀和發(fā)展趨勢(shì)[J]. 液壓氣動(dòng)與密封, 2016(8): 68.

LIU Baojie, YANG Qingwen, WU Xiang.Current research and development trend of fault diagnosis technology for hydraulic system[J].Hydraulics Pneumatics & Seals, 2016(8): 68.

[2] TAO X C, LU C, LU C, et al. An approach to performance assessment and fault diagnosis for rotating machinery equipment[J]. EURASIP Journal on Advances in Signal Processing, 2013(1): 1.

[3] JIA D Q, SHI B H. Research of shield machine fault prediction system based on improved Elman network algorithm[C]// Proceedings of the 33rd Chinese Control Conference. Shanghai:[s.n.], 2014.

[4] 黃克, 趙炯, 周奇才, 等. 基于多變量統(tǒng)計(jì)過程監(jiān)控的盾構(gòu)故障診斷[J]. 中國工程機(jī)械學(xué)報(bào), 2012, 10(2): 222.

HUANG Ke, ZHAO Jiong, ZHOU Qicai, et al. Fault diagnosis on shield machines based on multivariable statistical process monitoring[J]. Chinese Journal of Construction Machinery, 2012, 10(2): 222.

[5] 文巧鈞. 基于狀態(tài)空間模型的復(fù)雜動(dòng)態(tài)過程監(jiān)測(cè)方法研究[D]. 杭州： 浙江大學(xué), 2015.

WEN Qiaojun. State space model based approaches for complex dynamic process monitoring[D]. Hangzhou: Zhejiang University, 2015.

[6] 李衛(wèi)東. 應(yīng)用多元統(tǒng)計(jì)分析[M]. 北京: 北京大學(xué)出版社, 2015.

LI Weidong. Applied multivariate statistical analysis[M]. Beijing: Peking University Press, 2015.

[7] 高會(huì), 李彥平. 基于殘差主元分析的多變量系統(tǒng)故障診斷方法及應(yīng)用[J]. 沈陽大學(xué)學(xué)報(bào)(自然科學(xué)版), 2016, 28(2): 141.

GAO Hui, LI Yanping. Multivariate system fault diagnosis methods and its applications based on residual principal component analysis [J].Journal of Shenyang University (Natural Science), 2016, 28(2): 141.

[8] BAKDI A, KOUADRI A, BENSMAIL A. Fault detection and diagnosis in a cement rotary kiln using PCA with EWMA-based adaptive threshold monitoring scheme[J]. Control Engineering Practice, 2017, 66: 64.

[9] 何小斌. 基于統(tǒng)計(jì)學(xué)方法的自適應(yīng)過程監(jiān)控與故障診斷[D]. 上海： 上海交通大學(xué), 2009.

HE Xiaobin. Adaptive process monitoring and fault diagnosis based on statistical methods[D]. Shanghai: Shanghai Jiao Tong University, 2009.

[10] TRENDAFILOV N T, JOLLIFFE I T. DALASS: Variable selection in discriminant analysis via the LASSO[J]. Computational Statistics & Data Analysis, 2007, 51(8): 3718.

[11] 朱志潔, 張宏偉, 韓軍, 等. 基于PCA-BP神經(jīng)網(wǎng)絡(luò)的煤與瓦斯突出預(yù)測(cè)研究[J]. 中國安全科學(xué)學(xué)報(bào), 2013, 23(4): 45.

ZHU Zhijie, ZHANG Hongwei, HAN Jun, et al. Prediction of coal and gas outburst based on PCA-BP neural network[J]. China Safety Science Journal, 2013, 23(4): 45.

[12] 陶建峰, 劉成良. 全斷面巖石隧道掘進(jìn)機(jī)液壓技術(shù)研究現(xiàn)狀[J]. 液壓與氣動(dòng), 2015(6): 1.

TAO Jianfeng, LIU Chengliang. Review of technical research for hydraulic system of tunnel boring machine[J]. Chinese Hydraulics & Pneumatics, 2015(6): 1.

[13] 李喜蓮. 盾構(gòu)刀盤驅(qū)動(dòng)液壓系統(tǒng)及其功率自適應(yīng)控制方法研究[D]. 杭州： 浙江大學(xué), 2007.

LI Xilian. Hydraulic system for cutterhead of shield based on self-adaptive power control method[D]. Hangzhou: Zhejiang University, 2007.

[14] ZHANG L, WU X, SKIBNIEWSKI M J. Simulation-based analysis of tunnel boring machine performance in tunneling excavation [J]. Journal of Computing in Civil Engineering, 2015, 30(4): 3.

[15] 楊華勇, 趙靜一. 土壓平衡盾構(gòu)電液控制技術(shù)[M]. 北京： 科學(xué)出版社, 2013.

YANG Huayong, ZHAO Jingyi. Electro-hydraulic control technology for EPB shield [M]. Beijing: Science Press, 2013.