電流自適應控制抑制開關磁阻電機轉矩脈動

黨選舉， 苗茂宇， 姜 輝， 伍錫如， 李 珊

(1.桂林電子科技大學 電子工程與自動化學院，廣西 桂林 541004；2.桂林電子科技大學 教學實踐部，廣西 桂林 541004)

開關磁阻電機為雙凸極變磁阻電機，轉子極既無繞組亦無永磁體，定子極繞有集中繞組，其運動由定、轉子間氣隙磁阻的變化產生，具有結構簡單、效率高、運行穩定可靠、成本低廉、易于維護等諸多優點。然而其雙凸極結構、電磁特性的高度非線性和強耦合性，導致其運行時轉矩脈動較大，由轉矩脈動導致的噪聲和振動問題嚴重制約其應用和發展。故開關磁阻電機轉矩脈動抑制成為近年來研究的熱點。

為了抑制轉矩脈動，國內外學者進行了多方面的研究，并取得大量研究成果。主流研究方向大體可以分為電機結構和控制策略兩個部分，在電機控制策略方面常用轉矩分配函數法(Torque Sharing Function,TSF)和直接轉矩控制法(Direct Torque Control,DTC)。其中轉矩分配控制多應用于抑制SRM(Switched Reluctance Motor)轉矩脈動[1]，該策略通過合適的分配函數，使轉矩在換相期間平滑過渡，加以合適的控制策略可使SRM輸出轉矩平穩跟蹤給定參考轉矩。文獻[2]對比分析了直接轉矩控制和轉矩分配控制兩種控制策略的控制效果，在磁鏈特性未知的情況下，TSF的控制效果更明顯；文獻[3]分別以線性TSF和余弦TSF控制設計各相轉矩，分析分配函數的不同對控制效果的影響；文獻[4]提出轉矩-電流的非線性模型，提高了模型的準確性，但是未給出未知參數的具體辨識過程；文獻[5]提出電流分配(Current Sharing Function,CSF)和磁鏈分配(Flux Linkage Sharing Function,FSF)控制策略，實現對電流或磁鏈的直接滯環控制，避開直接尋找轉矩-電流的非線性關系，控制靈敏度高；文獻[6]引入有限差分擴展卡爾曼濾波(Finite-Difference Extended Kalman Filter,FDEKF)預測轉速，實現無速度傳感器魯棒控制，優化電機的控制結構；文獻[7]在傳統轉矩分配控制的基礎上引入迭代學習控制器，以轉矩偏差最小為控制目標，對參考電流進行迭代學習，有效抑制了SRM的轉矩脈動。

上述方案的主體控制思路均是從SRM轉矩-電流的非線性關系角度，避開或間接補償其非線性關系，但存在兩方面問題，一方面未給出非線性關系的具體辨識過程，另一方面未對參考電流進行實時的反饋補償，致使其非線性關系難以準確獲得，進而導致控制效果不佳的缺陷。

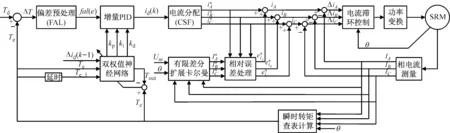
圖1 電流自適應控制抑制開關磁阻電機轉矩脈動系統框圖

1 基于雙權值神經網絡的SRM自適應電流控制算法

SRM是一個變結構、變參數的強非線性系統，難以獲得精確的數學模型。針對傳統轉矩分配控制的缺點，該文提出DWNN來辨識Δid和Te的非線性關系，進而求得對應參考電流，其控制結構如圖2所示。

Δid和Te的非線性關系在高維空間中為一張復雜曲面，改進后的DWNN可以根據需要自適應構造出不同類型的超曲面去逼近，有效克服經典神經網絡只能用單一類型曲面逼近的弊端。故相對而言，DWNN能夠更好地逼近SRM的非線性，其學習結構如圖3所示。

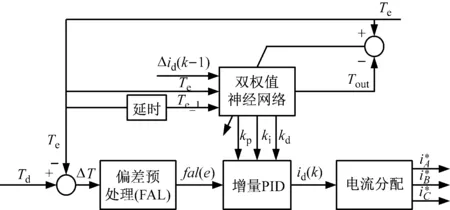
圖2 基于轉矩偏差的DWNN自適應PID控制結構

Fig.2 Structure of self-adaptive PID control of DWNN based on torque deviation

1.1 改進的DWNN的自適應PID控制

1.1.1 改進的DWNN

傳統DWNN隱含層輸出[8]為

圖3 DWNN的學習結構

(1)

式(1)存在兩點不足:①次冪b為固定值，無法根據需要自適應構造不同類型的超曲面，則控制的快速性及準確性降低；②兩種權值的次冪都為b，次冪b的改變同時改變兩種權值的大小，導致控制靈敏度降低。

該文針對其不足進行改進，加入次冪的自適應調整，改進后的神經元函數為

(2)

式中：hj為隱含層輸出函數；f(x)為激活函數；Tout為辨識網絡輸出轉矩；wij為方向權值；qij為核心權值；vj為輸出權值；bij為可調整的次冪；該文取a=0.1，m=1。

辨識器的性能指標函數為

(3)

根據梯度下降法，輸入方向權值、核心權值、輸出權值及次冪bij的迭代算法為

(4)

式中：η為權值調整學習率；ηb為次冪調整學習率。

1.1.2 增量自適應PID的控制

參考電流id(k)為DWNN自適應PID控制算法的輸出u(k)，以DWNN辨識的轉矩偏差最小為目標進行權值調整，進而調整增量PID的三個系數kp、ki、kd，求出控制量的增量Δu(k)，與k-1時刻的控制量u(k-1)疊加，可求得控制量u(k)，經典的增量式PID公式為

u(k)=u(k-1)+Δu(k)

(5)

Δu(k)=kp(e(k)-e(k-1))+kie(k)+

kd(e(k)-2e(k-1)+e(k-2))

(6)

式中:e(k)為k時刻的轉矩偏差。

該文引入非線性函數對轉矩偏差進行預處理，使控制器實現理想的控制方式，即“小誤差，大增益，大誤差，小增益”[9]，具體計算公式[10]為

(7)

式中:α為非線性因子;δ為線性區間長度。取

(8)

由上可知，經偏差預處理后的增量PID變為

(9)

增量PID系數kp、ki、kd的調整采用梯度下降法，選取性能指標函數為

(10)

經偏差預處理后，kp、ki、kd的迭代算法為

(11)

(12)

式中:k時刻的控制量增量Δid(k)未知，由于采樣時間短，故用k-1時刻的增量Δid(k-1)近似代替，由此帶來的計算誤差可以通過學習率的調整來進行修正。

1.2 電流分配函數的選擇

常用的轉矩分配函數有直線型、指數型、正弦型和立方型四種，綜合比較四種分配函數的運算量和控制效果，該文選擇立方分配函數。

立方分配函數的數學表達式為

(13)

其中:θ為轉子位置角;θon為開通角;θov為換相重疊角。

(14)

2 基于有限差分擴展卡爾曼濾波預測電流的前饋補償控制

2.1 基于FDEKF預測電流的總體設計

為實現對參考電流的實時控制，該文提出了參考電流的前饋補償控制，通過FDEKF一步預測出電流，將其與DWNN輸出的參考電流之差疊加到參考電流，控制輸出電流逼近參考電流，進而使輸出轉矩穩定在給定的參考轉矩附近，間接抑制SRM的轉矩脈動。其基本框架如圖4所示，在電機單相導通的情況下，電機模型相對較準確，如果噪聲為已知高斯噪聲，則FDEKF可實時捕捉SRM的非線性特性，準確預測出非線性電流。

圖4 基于FDEKF預測電流的前饋補償控制結構

Fig.4 Structure of feed-forward compensation control based on the FDEKF to predict current

SRM的相電流、轉速和角度的狀態方程為

(15)

2.2 基于FDEKF的電流預測

A、B、C三相電流的預測過程類似，該文以B相電流預測為例，詳細介紹FDEKF預測電流的實現流程[11]。取狀態量Xm=[Imwθ]T，令m=B,則XB的預測過程為

(1) 濾波初始化

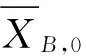
式中：Q為過程激勵噪聲協方差矩陣；R為觀測噪聲協方差矩陣。

(2) 狀態及相應誤差協方差陣的預測

XB,k+1/k=f(XB,k/k)+ωk

(16)

式中：ωk為過程激勵噪聲矩陣；XB,k/k為第k次狀態預測值；f(x)為狀態轉移函數，由式(15)可得。

用一階中心方差得出誤差協方差矩陣為

(17)

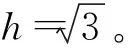
(3) 測量值預測

YB,k+1/k=HXB,k+1/k

(18)

式中：H為觀測矩陣。

(4) 卡爾曼增益計算

KB=PB,k+1/kHT(HPB,k+1/kHT+R)-1

(19)

(5) 狀態預測值及協方差矩陣的更新

(20)

式中：YB,k+1為實際測量值；I為單位陣。

(6) 協方差矩陣的Choleskey分解

SXB,(k+1/k+1)={chol(PB,k+1/k+1)}

(21)

同理，取m=A或m=C可推出

XA,k+1/k+1=XA,k+1/k+KA(YA,k+1-YA,k+1/k)

(22)

XC,k+1/k+1=XC,k+1/k+KC(YC,k+1-YC,k+1/k)

(23)

式中:XA,k+1/k和XC,k+1/k分別為狀態XA和XC的預測值，借鑒式(16)求得；YA,k+1/k和YC,k+1/k為狀態XA和XC的預測測量值，借鑒式(18)求得；KA與KC分別為狀態XA和XC的卡爾曼增益，借鑒式(19)求得。

由上可知，FDEKF預測的三相電流為

(24)

以轉子位置角θ為參考，在單相導通區，按上述方法求得單相導通電流即可，在換相區，求得導通相和關斷相電流即可，其余相電流值為0，無需預測。

2.3 參考電流的前饋補償

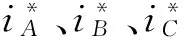
(25)

前饋補償后得到三相控制電流iA、iB和iC為

(26)

3 仿真驗證與分析

為驗證該文所提控制策略的有效性，在Matlab/Simulink仿真環境下，對開關磁阻電機控制系統進行建模，加入控制算法進行仿真研究。其中，電機模型為采用12/8極結構的SRM非線性模型[12]，電機模型的主要參數選擇如表1所示。

3.1 SRM的控制性能指標

SRM的控制性能指標選擇轉矩脈動系數[13]，其定義為

(27)

表1 SRM的主要參數

式中：Tmax為SRM的最大瞬時轉矩；Tmin為SRM的最小瞬時轉矩；Tav為SRM的平均轉矩。

3.2 仿真結果對比

該文對傳統轉矩分配控制進行仿真，結果如圖5所示，可知轉矩脈動較大，轉矩脈動系數為46.42%。圖6為基于轉矩偏差的DWNN自適應PID的控制結果，轉矩脈動明顯減小，穩態時轉矩脈動系數可達2.56%。電流自適應控制抑制SRM轉矩脈動的控制結果如圖7所示，可知SRM的輸出轉矩能夠快速平穩的跟蹤給定轉矩，系統響應快，轉矩超調量和轉矩脈動都很小，穩態時轉矩脈動系數為1.65%。綜合對比見表2，該文所提電流自適應控制抑制SRM轉矩脈動控制策略的控制效果明顯，有效減小轉矩脈動。

圖8為傳統轉矩分配控制下的單相參考電流；圖9為電流自適應控制抑制SRM轉矩脈動的單相參考電流波形，對比可知，處理后的參考電流具有SRM的非線性特性，在一定程度上修正了非線性電感不可測所導致的控制偏差，大幅度減小了轉矩脈動。

圖5 傳統轉矩分配(TSF)控制的轉矩波形

Fig.5 Torque waveform of traditional TSF control

圖6 基于轉矩偏差的DWNN自適應PID控制的轉矩波形

Fig.6 Torque waveform of self-adaptive PID control of DWNN based on torque deviation

圖7 電流自適應控制抑制SRM轉矩脈動的轉矩波形

Fig.7 Torque waveform of torque ripple suppression of SRM based on current self-adaptive control

圖8 傳統轉矩分配控制的電流波形

圖9 電流自適應控制抑制SRM轉矩脈動的電流波形

Fig.9 Current waveform of torque ripple suppression of SRM based on current self-adaptive control

表2 轉矩脈動系數對比

4 結 論

該文以傳統轉矩分配為基礎，為改善系統動態性能，加入偏差預處理，實現“小誤差，大增益，大誤差，小增益”的控制，以此為基礎設計了DWNN自適應PID的電流控制，得到三相參考控制電流，并采用FDEKF一步預測電流，構成參考電流的前饋補償控制，實現SRM轉矩的平滑輸出，達到抑制SRM轉矩脈動的目的。仿真結果表明，該文所提電流自適應控制抑制開關磁阻電機轉矩脈動的控制策略，穩態時輸出轉矩快速地收斂到給定轉矩，大幅減小轉矩脈動。

[1] CHOI C, KIM S, KIM Y, et al. A new torque control method of a switched reluctance motor using a torque-sharing function[J]. IEEE Transactions on Magnetics, 2002, 38(5):3288-3290.

[2] SUN Q, WU J, GAN C, et al. Investigation of direct torque control and torque sharing function strategy for switched reluctance motor applications[C]∥ International Conference on Electrical Machines and Systems. Pattaya: IEEE, 2015：864-868.

[3] KURIAN S, NISHA G K. Torque ripple minimization of SRM using torque sharing function and hysteresis current controller[C]∥ International Conference on Control Communication & Computing India. Trivandrum: IEEE, 2015：149-154.

[4] YE J, BILGIN B, EMADI A. An offline torque sharing function for torque ripple reduction in switched reluctance motor drives[J]. IEEE Transactions on Energy Conversion, 2015, 30(2):1-10.

[5] WANG J J. A common sharing method for current and flux-linkage control of switched reluctance motor[J]. Electric Power Systems Research, 2016, 131:19-30.

[6] OUDDAH N, LOUKKAS N, CHAIBET A, et al. Experimental evaluation of second sliding modes observer and extended Kalman filter in a sensorless robust control of switched reluctance motor for EV application[C]∥Control and Automation. Torremolions: IEEE, 2015:986-992.

[7] 黨選舉, 肖逢, 林誠才. 基于電流迭代優化的SRM總轉矩TSF閉環控制[J]. 電氣傳動, 2015, 45(8):41-46.

DANG Xuanju, XIAO Feng, LIN Chengcai. Closed loop control of total torque TSF for switched reluctance motor based on current iteration optimization[J]. Electric Drive, 2015, 45(8): 41-46.

[8] 曹宇. 雙權值人工神經網絡用于數據擬合的研究[D]. 北京：中國科學院半導體研究所, 2002:1-45.

[9] 韓京清. 從PID技術到“自抗擾控制”技術[J]. 控制工程, 2002, 9(3):13-18.

HAN Jingqing. From PID to "active disturbance rejection control technique"[J]. Control Engineering of China, 2002, 9(3): 13-18.

[10] 劉福才, 陳鑫, 賈亞飛,等. 模糊自抗擾控制器在撓性航天器振動抑制中的應用[J]. 振動與沖擊, 2015,34(9):9-14.

LIU Fucai, CHEN Xin, JIA Yafei, et al. Application of fuzzy auto disturbance rejection controller in flexible spacecraft vibration suppression[J]. Journal of Vibration and Shock, 2015,34(9): 9-14.

[11] WU C, HAN C. Strong tracking finite-difference extended Kalman filtering for ballistic target tracking[C]∥IEEE International Conference on Robotics & Biomimetics. Sanya: IEEE, 2007:1540-1544.

[12] 王宏華. 開關磁阻電動機調速控制技術[M]. 2版.北京：機械工業出版社, 2014:1-264.

[13] DOWLATSHAHI M, NEJAD S M S, MOALLEM M, et al. Torque ripple reduction of switched reluctance motors considering copper loss minimization[C]∥IEEE International Conference on Industrial Technology. Busan: IEEE, 2014:858-865.