斜拉橋橫向減震振動臺試驗

易 江， 孫平寬， 李建中

(1.同濟大學 土木工程防災國家重點實驗室，上海 200092；2.中國公路工程咨詢集團有限公司，北京 100089)

斜拉橋作為交通運輸的樞紐工程，其抗震性能一直得到關注和研究。在縱橋向，我國的斜拉橋普遍采用飄浮體系，并在塔梁間設置黏滯阻尼器進行減震，因而斜拉橋縱向的抗震性能一般較好。在橫橋向，為滿足正常使用下的性能要求，斜拉橋通常在塔梁間設置橫向抗風支座，結構橫向剛度較大；在地震作用下，結構橫向地震響應較大，結構可能出現損傷。如在1999年Chi-Chi地震中集鹿大橋的橋塔在橫向產生了嚴重震害[1]。因此，在高烈度地區，如何減小斜拉橋橫向地震反應成為斜拉橋抗震設計的重點。

彈塑性阻尼器具有穩定的滯回特性、較好的疲勞特性和易于更換等優點[2]。在正常使用狀態下，阻尼器不屈服，提供較大的彈性剛度來滿足抗風和使用荷載要求；在強震作用下，阻尼器產生屈服，通過塑性變形來耗散地震能量，達到減震的目的[3]。目前，國內已有數座斜拉橋采用彈塑性阻尼器來控制結構橫向地震響應[4-5]。

另一方面，在最近的數次大地震中，如1995年日本阪神地震、1999年臺灣集集地震和2008年汶川地震，都記錄到了一定數量的近場地震動[6]。與常見的遠場地震動相比，近場地震動通常含有長周期的速度脈沖、較大的速度峰值和豐富的長周期譜值成分，將會對斜拉橋產生顯著的影響[7]。近年來，一些學者對近場地震作用下斜拉橋的抗震性能進行了研究。Wesolowsky等[8]研究了大跨斜拉橋在近場地震作用下的響應特點及鉛擠壓阻尼器和黏滯阻尼器等裝置的減震效果；蔡茂江等[9]針對斜拉橋半漂浮體系分析了近場地震作用下黏滯阻尼器合理的參數。但這些研究多集中在近場地震作用對斜拉橋縱向地震響應的影響，還較少涉及到橫向地震響應。

為此，本文以一座高烈度區的獨塔斜拉橋為工程背景，設計并建造了一座1∶20縮尺比的微粒混凝土斜拉橋全橋模型，在同濟大學多功能振動臺實驗室對該模型進行了橫橋向振動臺試驗。試驗中分別采用了一條遠場地震動和一條近場地震動作為地震動輸入，探討了遠場和近場地震作用下彈塑性阻尼器對斜拉橋橫向地震反應的減震效果。最后，建立了振動臺試驗模型的有限元模型，將數值和試驗結果進行對比分析。

1 試驗模型設計

1.1 背景工程

背景工程為一座跨徑分布為230 m+230 m的獨塔斜拉橋，如圖1所示。該橋采用“A”型C50混凝土橋塔，塔高150 m，其中塔底至橫梁、橫梁至斜塔柱交叉點、塔柱交叉點至塔頂高度分別為34 m、72 m和44 m。過渡墩為門式框架雙柱墩，墩高34 m，混凝土材料為C40。加勁梁為全封閉流線型扁平鋼箱梁，梁高3.2 m，寬34 m。

(a)橋塔(b)鋼箱梁(c)全橋平面圖

圖1 某斜拉橋總體布置圖(單位：m)

Fig.1 Schematic of one cable-stayed bridge (unit: m)

1.2 模型設計

1.2.1 相似比

考慮到振動臺面尺寸及承載能力等條件，本試驗模型縮尺比最終確定為1∶20。模型中橋塔、橋墩等采用微粒混凝土、鍍鋅鐵絲和鐵絲網來模擬原型混凝土和鋼筋，混凝土構件彈性模量相似常數為0.3。主梁采用鋼材制作，彈性模量相似常數為1。為了考慮重力的影響，加速度相似常數取為1。應用量綱分析法推導其余物理量的相似常數，見表1。按照上述相似常數設計得到試驗模型總長為23 m，模型振動臺布置圖見圖2。

表1 模型相似常數

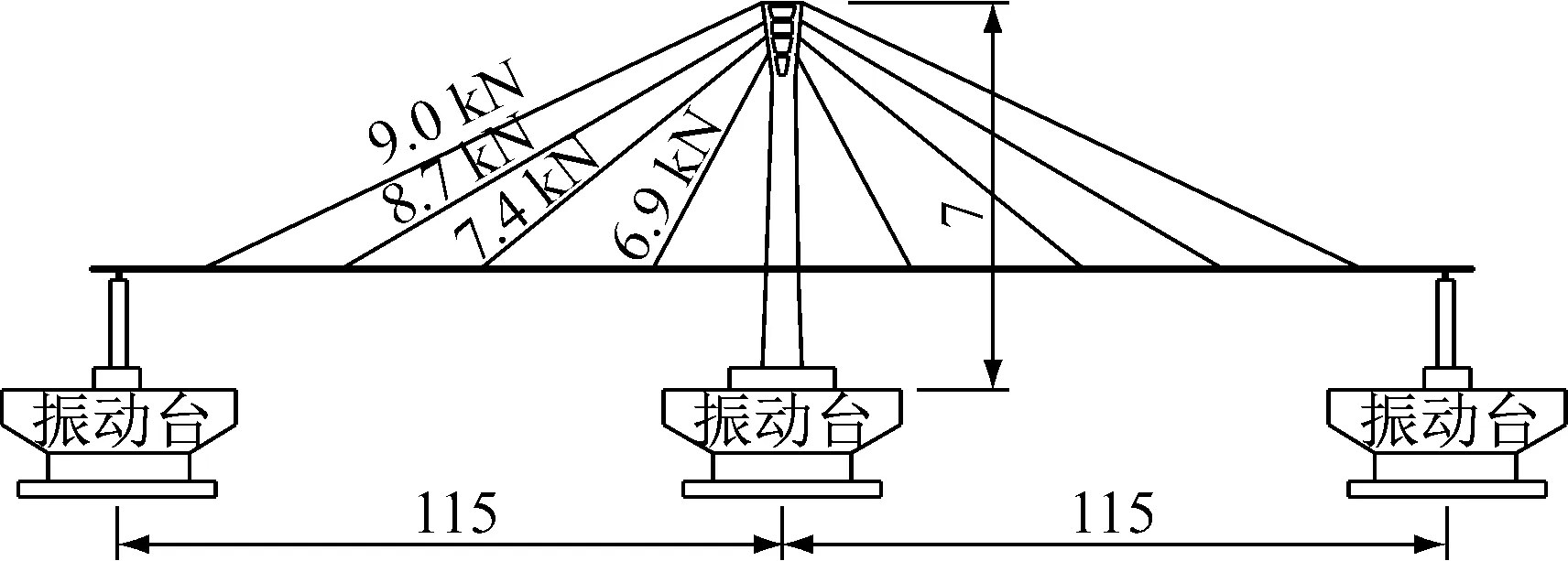
圖2 試驗模型振動臺布置圖(單位：m)

1.2.2 截面設計

若嚴格按1∶20幾何相似比，橋塔、主梁、墩柱等截面將會非常小，不利于模型加工以及后期安裝。為此，采用剛度等效原則進行截面設計，即保證橋塔、主梁、墩柱等截面的抗彎剛度嚴格相似，忽略了軸向剛度和抗扭剛度不能嚴格相似的影響[10]。橋塔和墩柱配筋依據抗彎能力和抗剪能力等效的原則進行設計。主梁采用空心矩形斷面，采用10 mm鋼板焊接拼裝。圖3給出了橋塔、主梁、墩柱截面設計圖。

斜拉索采用8 mm鋼絲繩模擬。為了滿足試驗模型索間距的構造要求，需要進行并索處理。并索步驟如下：①根據索間距構造要求將34對拉索縮減為8對，拉索在主梁上等間距分布；②將原型拉索豎向總分力均分至每根拉索，計算模型拉索索力，保證拉索豎向分力等效；③計算模型成橋線型，根據成橋線型與原橋一致的原則對索力進行微調。圖2中給出了模型最終成橋索力。

1.2.3 配重設計

在振動臺試驗中，結構本身慣性力通常是作用在結構上的主要荷載，試驗時需要滿足模型質量相似比。但依靠試驗模型自重是達不到根據相似比計算出試驗模型的理論質量，因而需要在對模型增加配重，各部位配重質量如表2所示。其中塔柱和墩柱的配重通過安裝配重箱來實現，箱中盛放24塊尺寸為15 cm×8 cm×5 cm的鑄鐵塊或鉛塊，單個鑄鐵塊或鉛塊質量分別為5 kg和7 kg。主梁配重采用成對的半圓鋼塊來實現，單個半圓鋼塊質量為25 kg。全橋振動臺試驗模型全貌見圖4。

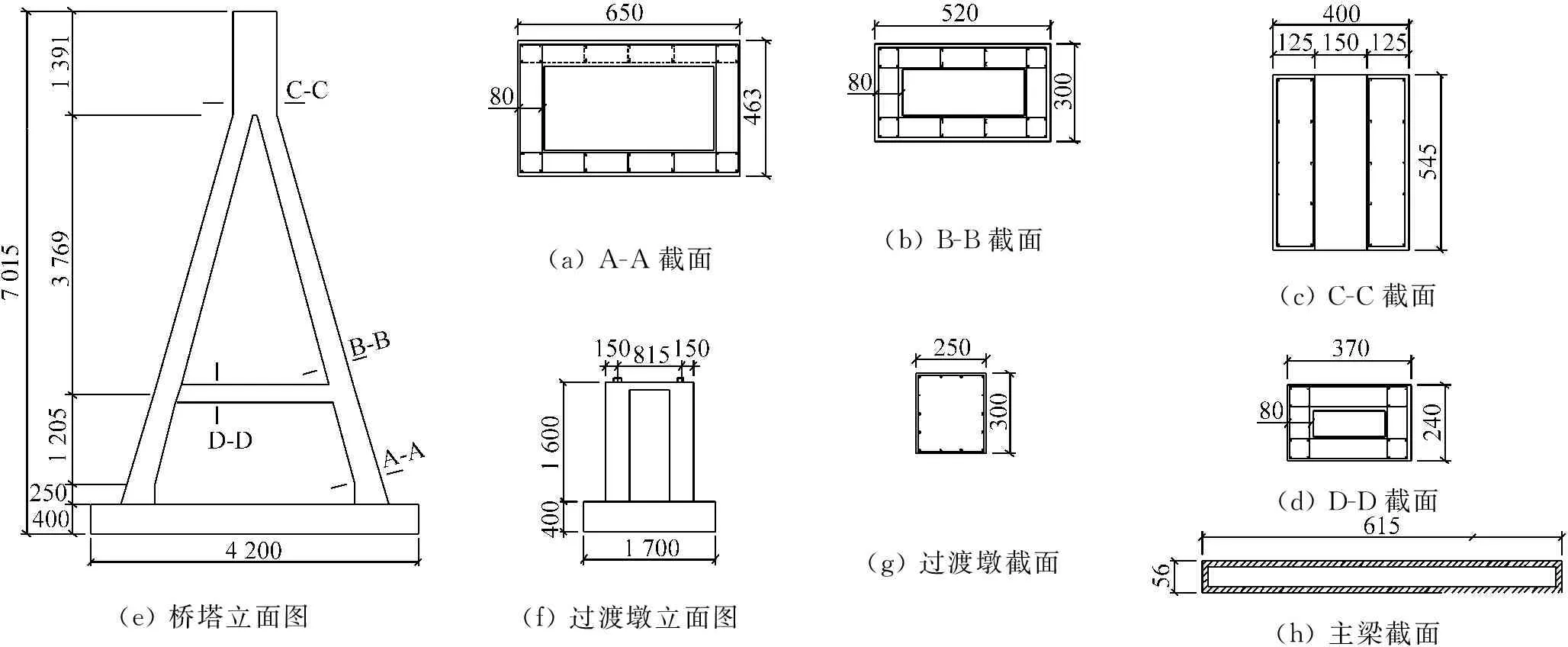
(e)橋塔立面圖(a)A-A截面(b)B-B截面(c)C-C截面(f)過渡墩立面圖(g)過渡墩截面(d)D-D截面(h)主梁截面

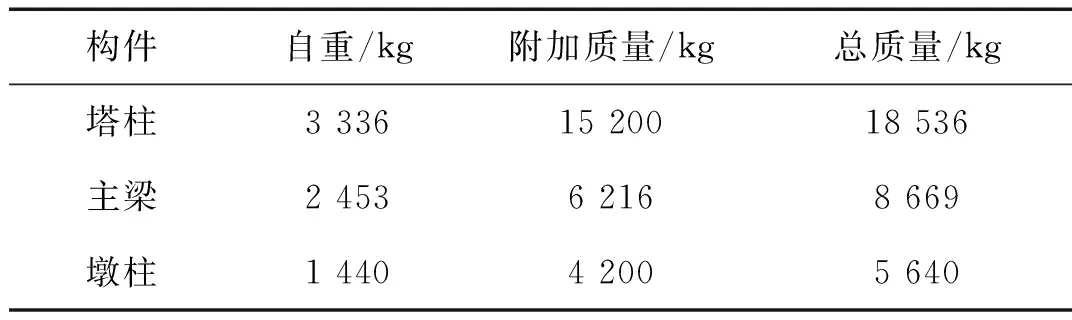
圖3 模型截面設計圖(單位：mm) Fig.3 Section design of tower model(unit：mm)

圖4 振動臺全橋試驗模型

1.2.4 彈塑性阻尼器設計

X型彈塑性阻尼器利用軟鋼的彈塑性特性滯回耗能，具有結構形式簡單,便于產品模數化等優點[11]。本試驗中采用X型彈塑性阻尼器作為減震裝置。X型彈塑性阻尼器設計時考慮屈服力和屈服位移與原型相似，細部尺寸如圖5所示。表3給出了彈塑性阻尼器的設計參數。

1.3 數據采集

本次試驗共有190個數據采集通道，采樣頻率為256 Hz。其中加速度計35個，位移計35個，應變片104個，力傳感器16個，具體分布見表4。

(a)

(b)

項目主塔處阻尼器過渡墩處阻尼器屈服力/kN5.251.875屈服位移/mm1.21.2屈后剛度比0.020.02極限位移/mm12.520

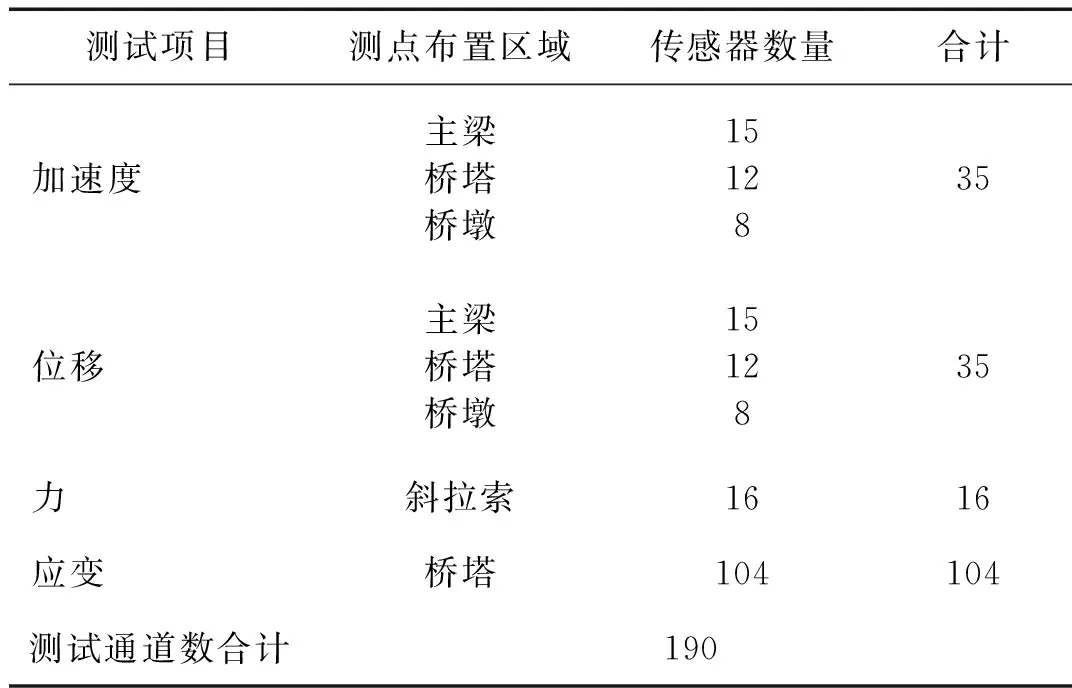
表4 全橋模型測點布置

2 試驗工況確定

2.1 橫向約束體系

塔梁、墩梁的連接方式對橋梁的靜、動力性能有很大的影響，地震作用下斜拉橋的受力和位移很大程度上取決于塔梁、墩梁間的連接方式[12]。本文考慮了如下兩種橫向約束方式對斜拉橋橫橋向地震響應的影響：①固定體系：塔-梁、墩-梁橫向固定約束；②阻尼體系：塔-梁、墩梁橫向采用彈塑性阻尼器連接。試驗沒有考慮樁土的相互作用，塔底、墩底均采用固接約束；縱橋向為半漂浮體系，采用滑動板式橡膠支座模擬縱向活動支座。

2.2 地震波

為研究近場、遠場地震作用下斜拉橋橫向地震響應，試驗分別采用一條遠場波和一條近場波對模型進行激勵。其中，遠場波是實橋場址處地震安全性評價報告提供的對應于E2概率水平(50年超越概率為2%)的人工擬合地震波，加速度峰值為0.4g；近場波選擇了1999年臺灣集集地震在TCU056測站記錄的實際地震波[13]，加速度峰值為0.349g。圖6給出了分別兩條波的加速度、速度時程曲線和反應譜。可見近場波包含了明顯的速度大脈沖和豐富的長周期譜值成分，代表了典型的近場地震動；而遠場波特征周期在0.4 s左右，代表了典型的中遠場地震動。

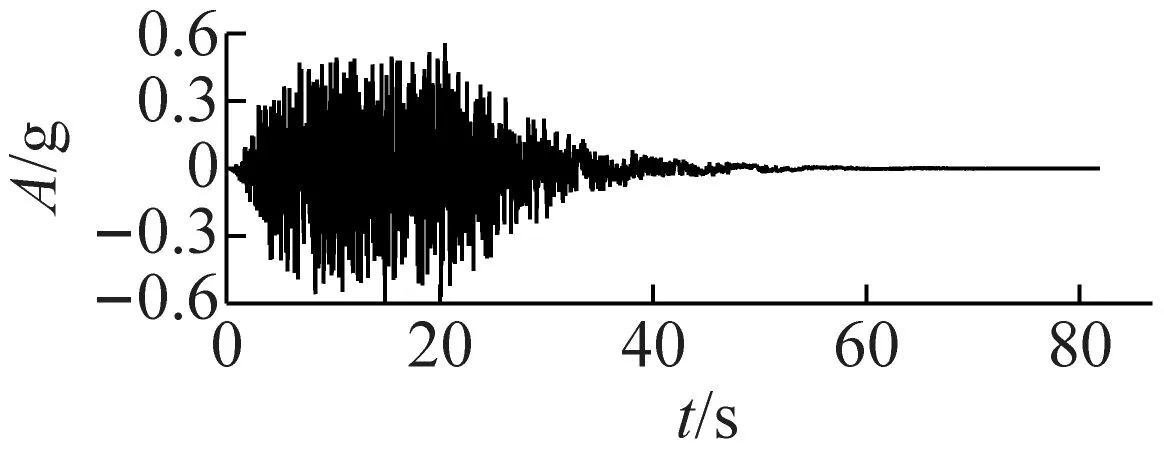
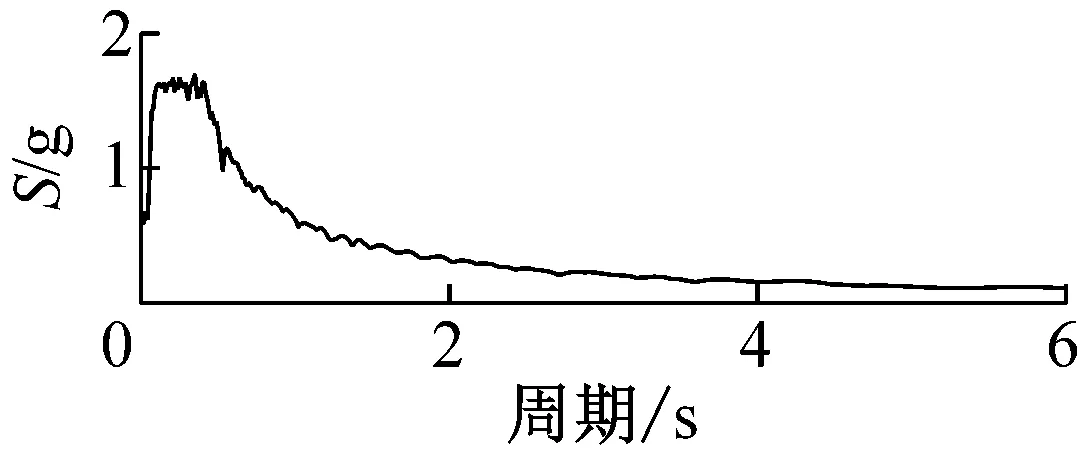
(a) 遠場波

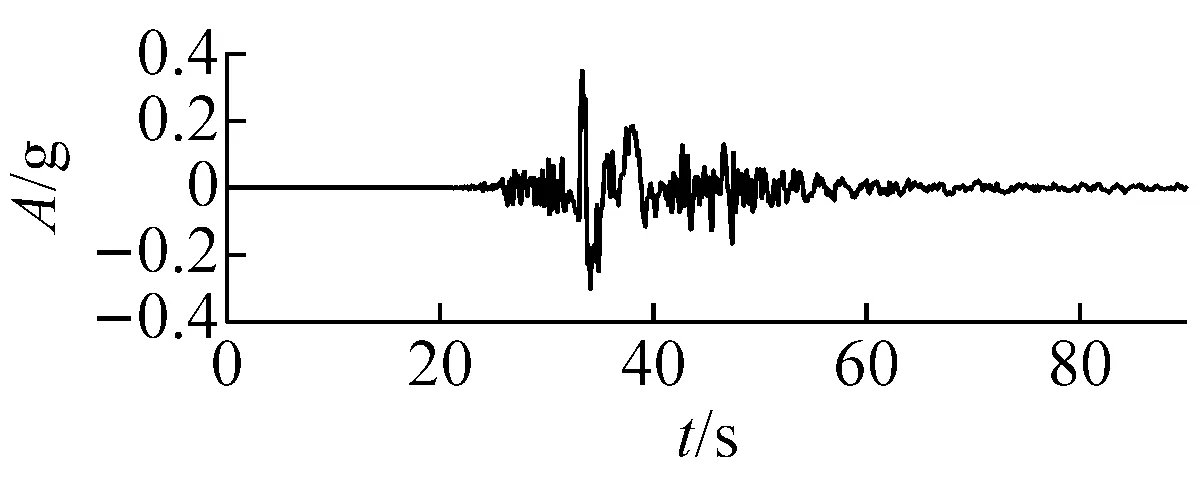
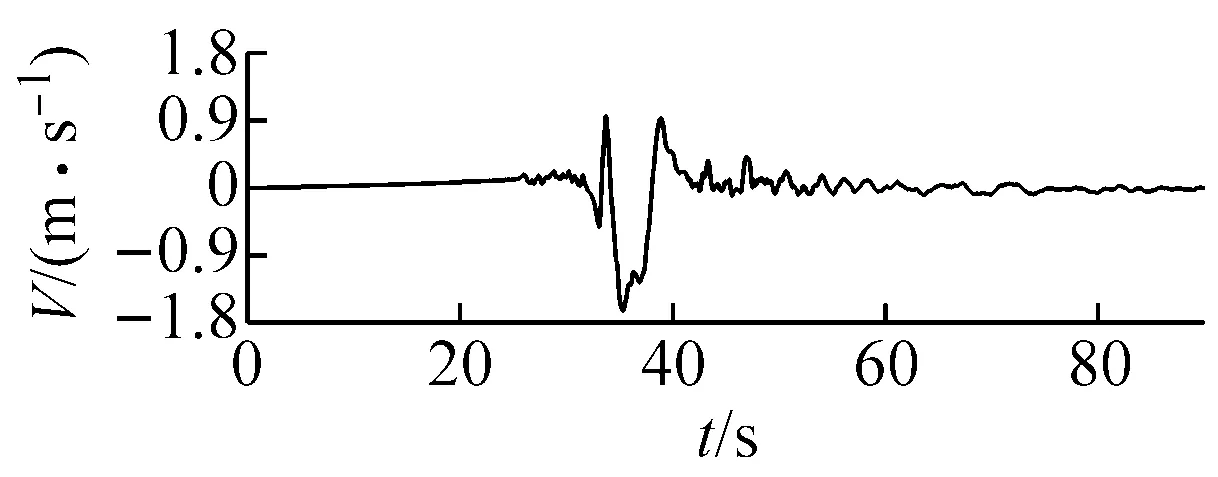
(b) 近場波

2.3 試驗工況

試驗中，分別對固定體系和阻尼體系進行兩條地震動加載試驗，試驗工況如表5所示。試驗中輸入遠場波的加速度峰值為0.1～0.4g，近場波的加速度峰值為0.1～0.3g。考慮到相似比關系，對輸入地震波的時間軸按照時間相似常數s=0.223 6進行壓縮。在每條地震波開始前和結束后均對模型進行白噪聲掃頻試驗，測量結構自振頻率等動力特征參數。

表5 試驗加載工況

3 試驗結果分析

3.1 動力特性

針對固定體系和阻尼體系，本試驗在不同地震動輸入前后均采用PGA=0.1g的白噪聲對試驗模型橫向進行掃頻試驗。以橋塔塔頂測點、橋塔處主梁測點的加速度反應對臺面白噪聲輸入信號做傳遞函數，得到傳遞函數的幅頻圖如圖7所示。通過圖7可以確定全橋模型的自振頻率，結果見表6。從表6可知，固定體系第一階為主梁橫向振動，主要是因為固定體系橫向擋塊與主梁沒有完全貼合，主梁橫向產生了小幅度振動。

(a) 固定體系

(b) 阻尼體系

Fig.7 Amplitude frequency diagram under white noise excitations

表6 自振頻率的比較

3.2 位移反應

圖8為遠場波和近場波輸入下(PGA=0.2g)固定體系和阻尼體系橋塔橫向位移沿塔柱高度的包絡圖。從圖8可以看出，在遠場波輸入下，阻尼體系塔柱位移響應均大于固定體系；在近場波輸入下，阻尼體系塔柱中部(2～5.5 m)位移響應比固定體系小，但塔頂位移比固定體系有所增大。

圖8 橋塔位移包絡圖(PGA=0.2g)

圖9給出了塔頂測點最大位移與輸入地震動加速度峰值PGA關系。圖9表明，在遠場波和近場波輸入下，固接體系和阻尼體系塔頂位移總體上均呈現隨輸入PGA的增大而線性增加的趨勢。對于相同的輸入PGA，遠場波作用下阻尼體系塔頂位移響應小于固定體系，而近場波作用下阻尼體系的塔頂位移大于固定體系。

圖9 塔頂最大位移隨臺面輸入PGA變化曲線

Fig．9 Incremental dynamic analysis curves of peak displacement of tower top

3.3 鋼筋應變響應

圖10給出了遠場波和近場波輸入下固定體系和阻尼體系塔底縱向鋼筋應變隨臺面輸入PGA的變化關系。從圖10可知，遠場波和近場波地震輸入下，阻尼體系塔底鋼筋應變均小于固定體系，表明近場和遠場地震輸入下彈塑性阻尼器均能有效減小橋塔的橫向地震響應。在遠場波輸入下，隨著輸入PGA的增加，阻尼體系塔底鋼筋應變相對于固定體系減小程度更明顯，當PGA=0.4g時，阻尼體系塔底鋼筋應變相對于固定體系減小了40%；在近場波輸入下，隨著輸入PGA的增加，阻尼體系對塔底鋼筋應變的減小程度基本不變，當PGA=0.3g時，阻尼體系塔底鋼筋應變約減小了10%。

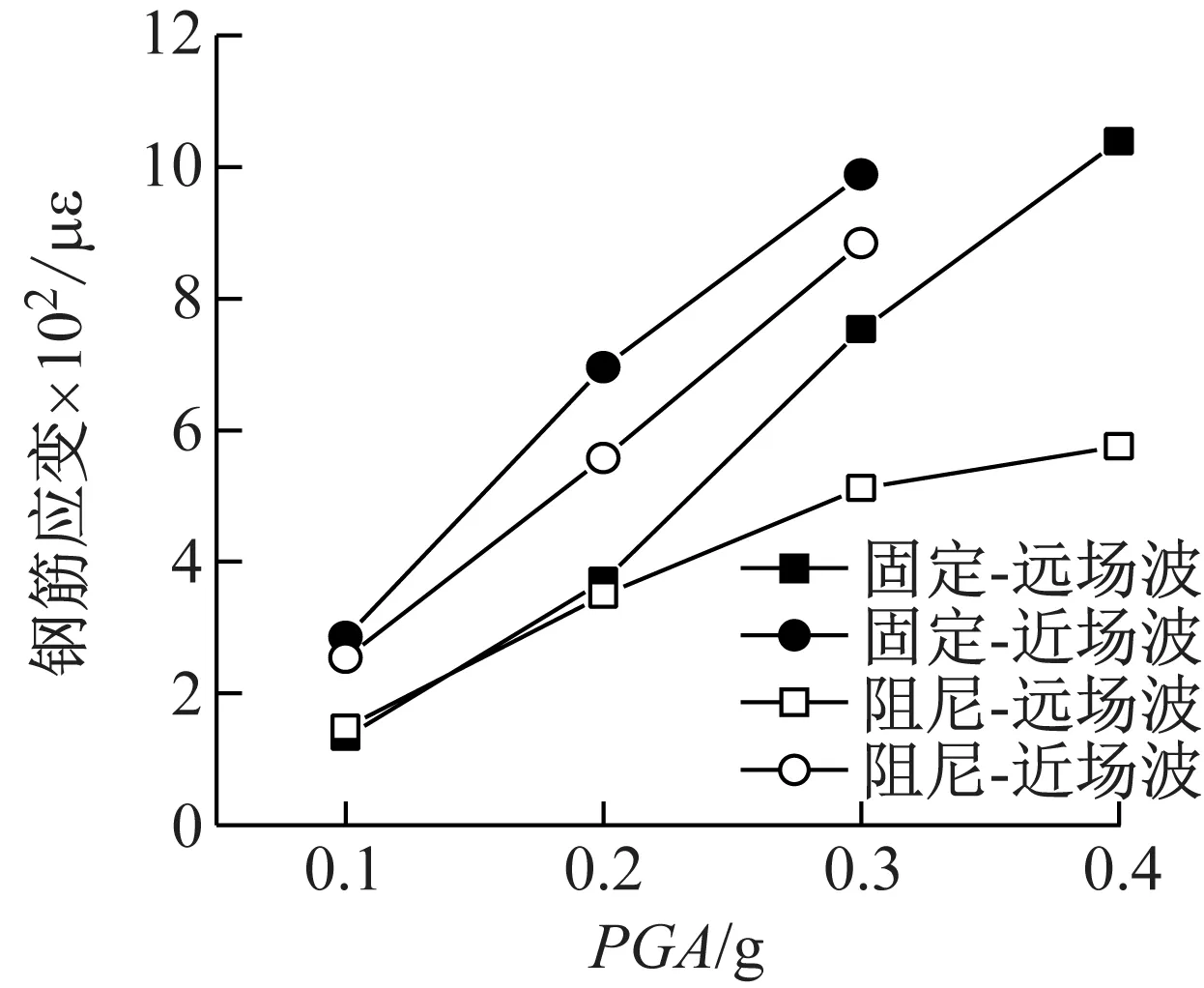
圖10 塔底鋼筋應變隨臺面輸入PGA的變化曲線

Fig.10 Incremental dynamic analysis curves of peak strains at tower bottom

3.4 阻尼器響應

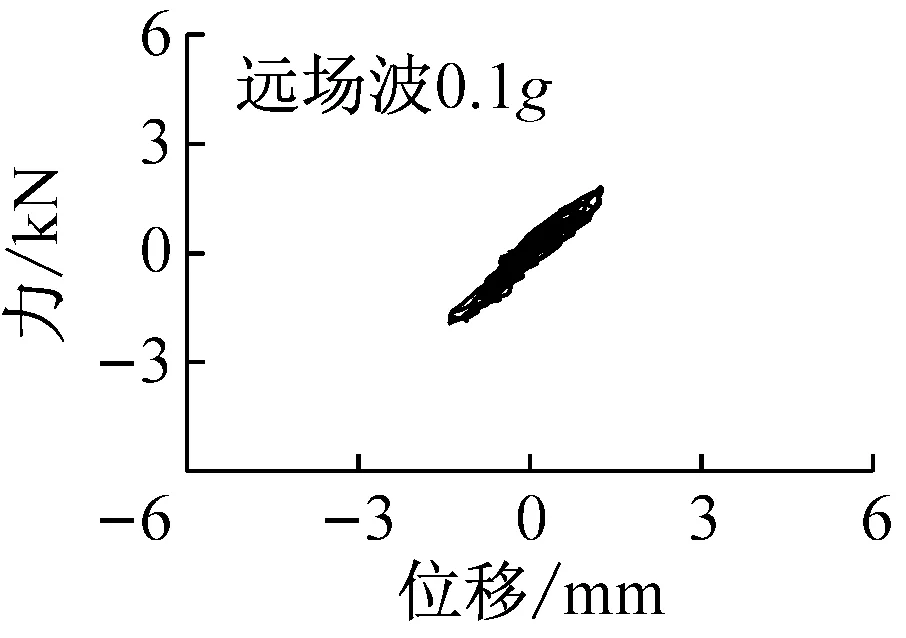
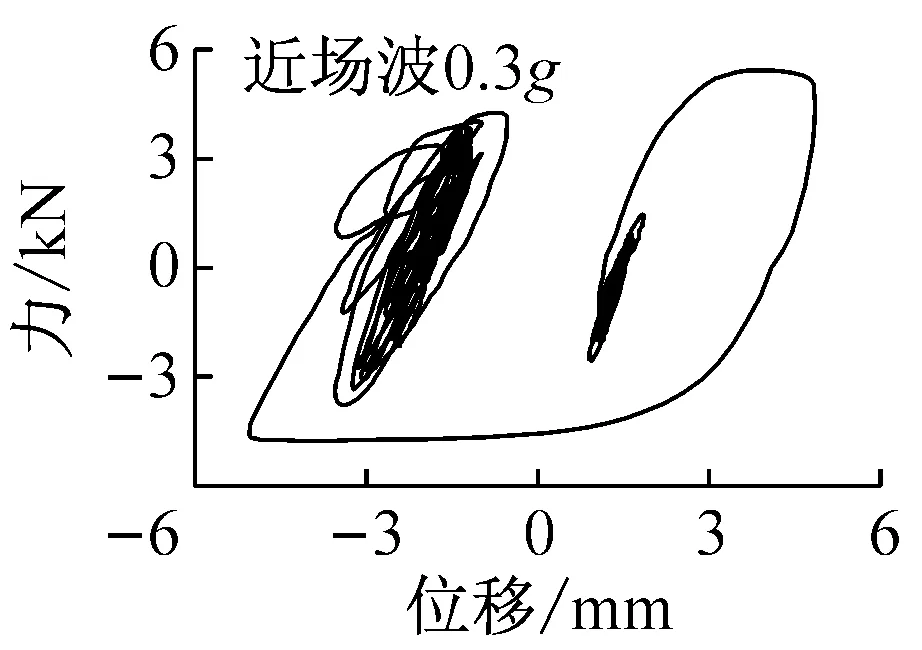
圖11給出了遠場波和近場波輸入下阻尼體系主塔處彈塑性阻尼器的滯回曲線，表7給出了各工況彈塑性阻尼器的地震響應。從圖11和表7可知，在遠場和近場波輸入下，當PGA較小時，阻尼器屈服程度較小，阻尼器變形、阻尼力和累計耗能均較小；隨著PGA的增大，阻尼器變形和累計耗能迅速增加，而由于阻尼器屈服，阻尼力增加不多。另外，圖11表明，在遠場波輸入下，滯回曲線包含了多個大面積滯回環，滯回環中心在原點附近，震后殘余變形較小，最大不超過0.25 mm。而在近場波輸入下，阻尼器變形較大，如在PGA=0.1g、PGA=0.2g和PGA=0.3g時阻尼器變形分別達到了遠場波作用時的3.6倍、4.3倍和4.6倍；同時滯回曲線出現了單個較大且不閉合的滯回環；當不閉合滯回環出現后，滯回環中心從原點轉移到其他位置，導致震后阻尼器出現較大的殘余變形，最大達到10.8 mm。

表7 彈塑性阻尼器的地震響應

3.5 數值與試驗結果對比

采用有限元軟件SAP2000，建立了背景工程的三維有限元模型。主塔、主梁、過渡墩均采用空間彈性梁單元模擬，考慮恒載軸力引起的幾何剛度影響；拉索采用空間桿單元模擬，采用Ernst等效彈模來考慮拉應力和自重垂度的影響，拉索與主梁、主塔均采用主從連接；塔-梁、墩-梁縱向均自由滑動，橫向根據固定體系或阻尼體系分別采用相應的連接方式；基礎固定約束。

(a)

(b)

(c)

(d)

(e)

(f)

(g)

圖12給出了PGA=0.2g時主梁位移時程曲線的振動臺實測值與數值模擬值對比圖；其中固定體系為跨中位置主梁位移響應，阻尼體系為中塔處主梁位移響應。從圖12可知：對于固定體系，數值結果與試驗結果有一定的誤差，主要原因是試驗時橫向擋塊與主梁有一定的間隙，數值模擬與試驗的邊界條件不完全相同；對于阻尼體系，數值結果與試驗結果較吻合，如在近場地震作用下數值模型較準確地反映了主梁的殘余位移。總體來看，有限元模型能較好地模擬地震和遠場地震作用下獨塔斜拉橋的橫向地震響應，可應用于獨塔斜拉橋橫向抗震設計。

(a) 固定體系-遠場波(0.2g)

(b) 固定體系-近場波(0.2g)

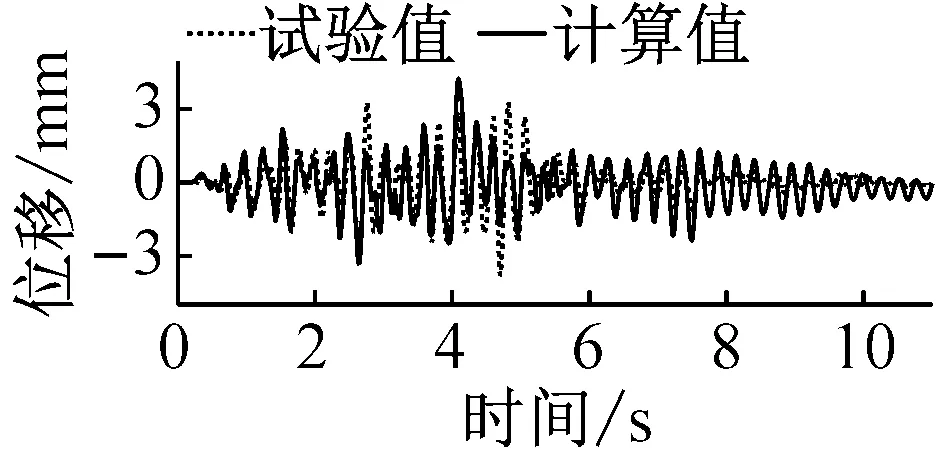
(c) 阻尼體系-遠場波(0.2g)

(d) 阻尼體系-近場波(0.2g)

4 結 論

以一座獨塔斜拉橋為研究對象，設計了1∶20大比例縮尺的全橋振動臺模型，進行了橫向固定體系和阻尼體系的振動臺模型試驗，研究了遠場和近場地震波輸入下阻尼體系的減震效果，主要結論如下：

(1) 在遠場波輸入下，阻尼體系塔頂位移相對于固定體系有所減小，而在近場波輸入下，阻尼體系塔頂位移有所增加。

(2) 在遠場波和近場波輸入下，阻尼體系塔底鋼筋應變響應均小于固定體系。其中，在遠場波輸入下，阻尼體系塔底鋼筋應變相對于固定體系最大減小了40%，而在近場波輸入下，阻尼體系鋼筋應變約減小了10%。

(3) 在遠場波和近場波輸入下，彈塑性阻尼器的變形和累計耗能均隨輸入PGA的增大而快速增加。在遠場波輸入下，阻尼器滯回曲線包含了多個較大的滯回環，加載完成后阻尼器殘余變形較小，可忽略不計；而在近場波輸入下，阻尼器滯回曲線出現一個較大但不閉合的滯回環，加載完成后阻尼器殘余變形較大。

(4) 通過比較主梁位移時程曲線的試驗結果和數值計算結果可以發現，數值結果與試驗結果較為接近、吻合較好。有限元模型可用于近場和遠場地震作用下獨塔斜拉橋的橫向抗震設計。

[1] CHANG K C, MO Y L, CHEN C C, et al. Lessons learned from the damaged Chi-lu cable-stayed bridge[J]. Journal of Bridge Engineering, 2004, 9(4):343-352.

[2] 徐艷紅．新型軟鋼阻尼器及其結構理論和試驗研究[D]．南京：東南大學，2013．

[3] 管仲國，李建中，朱宇. 彈塑性阻尼支座用于自錨式懸索橋減震設計[J]. 同濟大學學報(自然科學版), 2009, 37(1): 6-12.

GUAN Zhongguo, LI Jianzhong, ZHU Yu. Elastic-plastic energy dissipating bearing for seismic design of self-anchored suspension bridge with single tower[J]. Journal of Tongji University (Natural Science), 2009, 37(1): 6-12.

[4] 童申家，謝祥兵，袁世營, 等. 高烈度區斜拉橋橫向約束方案優化分析[J]. 土木建筑與環境工程, 2015, 37(4): 36-44.

TONG Shenjia, XIE Xiangbing, YUAN Shiying, et al. Optimal analysis of the lateral constraint systems for cable-stayed bridge in high intensity region[J]. Journal of Civil, Architecture & Environment Engineering, 2015, 37(4): 36-44.

[5] 王雷，梁立農，羅霞, 等. 柔梁矮塔斜拉橋抗震體系和減隔震措施研究[J]. 廣東公路勘察設計, 2015, 28(2): 13-18.

WANG Lei, LIANG Linong, LUO Xia, et al. Research on seismic system and seismic reduction and isolation measure of low pylon cable-stayed bridge with flexible girder[J]. Guangdong Highway Survey and Design, 2015, 28(2): 13-18.

[6] MAVROEIDIS G P, DONG G, PAPAGEORGIOU A S. Near-fault ground motions, and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems[J]. Earthquake Engineering & Structural Dynamics, 2004, 33(9): 1023-1049.

[7] 李勇，閆維明，陳彥江，等. 大跨斜拉橋的近斷層地震響應及減震控制[J]. 防災減災工程學報, 2010, 30(5): 479-486.

LI Yong, YAN Weiming,CHEN Yanjiang, et al. Seismic response analysis and control of long-span cable-stayed bridges under near-fault earthquakes[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(5): 479-486.

[8] WESOLOWSKY M J, WILSON J C. Seismic isolation of cable-stayed bridges for near field ground motions[J]. Earthquake Engineering & Structural Dynamics, 2013, 32(13): 2107-2126.

[9] 蔡茂江，徐艷，李建中. 近場地震輸入時斜拉橋黏滯阻尼器參數分析[J]. 上海應用技術學院學報(自然科學版), 2013, 13(1): 17-23.

CAI Maojiang, XU Yan, LI Jianzhong. Parametric study on the viscous dampers used for a cable-stayed bridge considering the near-fault earthquakes[J]. Journal of Shanghai Institute of Technology (Natural Science), 2013, 13(1):17-23.

[10] GAREVSKI M A, SEVERN R T. Damping and response measurement on a small-scale model of a cable-stayed bridge[J]. Earthquake Engineering & Structural Dynamics, 1993, 22(1): 13-29.

[11] VASSEGHI A. Energy dissipating shear key for precast concrete girder bridge[J]. Scientia Iranica, 2011, 18(3): 296-303.

[12] 葉愛君，胡世德，范立礎. 斜拉橋抗震結構體系研究[J]. 橋梁建設, 2002, 32(4): 1-4.

YE Aijun, HU Shide, FAN Lichu. Research on aseismic structural system of cable-stayed bridge[J]. Bridge Construction, 2002, 32(4): 1-4.

[13] MAVROEIDIS G P, PAPAGEORGIOU A S. A mathematical representation of near-fault ground motions[J]. Bulletin of the Seismological Society of America, 2003, 93(3): 1099-1131.