一種基于均方比值的人致結構振動加速度響應信號篩選方法

楊 娜， 胡浩然， 戴 璐

(北京交通大學 土木建筑工程學院，北京 100044)

在對人群激勵下樓板振動加速度響應信號進行分析時，人的突發行為(如突然的跑、跳)、監測儀器內部電流引起的噪聲以及其他因素都會引起采集到的信號偏離實際值，產生異常信號，如果異常的信號在預處理中沒有被剔除，會影響后續的振動評估以及其他相關工作的可靠性[1]。

目前常用的信號預處理包括以下幾個方面：①去除信號的趨勢項；②對信號進行平滑處理；③濾波；④對異常值進行剔除[2]。從處理方法上來看，可以分為頻域方法和時域方法，振動信號的時域特征表現為振幅、周期、相位等特性，其頻域特征表現為頻率、能量等特性[3]。常用的預處理方法包括最小二乘法，五點三次平滑法、高低通濾波、小波變化、拉依達準則、肖維勒準則、格拉布斯準則和狄克遜準則[4]等等。這些方法在一定程度上能還原信號的真實信息，但對于長時間監測的大量信號，僅僅通過普通的預處理并不能完全剔除異常信號，而未被剔除的異常信號會影響后續結構振動評估。

本文提出了一種進行信號篩選的參數和方法，該參數為人致振動響應加速度信號的均方根值和加權均方根值的比值，它可以對采集到的響應信號進行快速的篩選，剔除不是由人群荷載引起的信號。為了探究該參數的性質，本文對該參數的理論表達式進行了推導，建立有限元模型對人致樓板振動進行模擬，來驗證該參數的性質，并通過現場振動試驗，證明了該參數的性質在實際情況下的應用。

為了方便后文闡述，人致振動響應加速度信號的均方根值和加權均方根值的比值簡稱為均方比值。

1 人致樓板振動響應均方根值理論推導

為了探究均方比值的性質，本文將單人在樓板上原地踏步引起的樓板振動的理論解擴展到多人在樓板上原地踏步，并推導了響應均方根值以及加權均方根值的表達公式，并給出了均方比值的公式，分析結構參數和人群荷載的參數對結果的影響。

1.1 均方根值計算公式

人群荷載激勵下樓板振動響應的加速度信號均方根值和加權均方根值之比本質上是對信號的頻譜組成的評價，為了探討不同的參數對均方比值的影響，基于理論推導給出了理想狀況下的均方比值的表達式，可以直觀的看出各種參數對均方比值的影響。

對于采集到的加速度響應a=(a1,a2,…,an)，n為加速度響應信號的長度，其均方根值，加權均方根值的計算方法為

(1)

(2)

Ratio=RMS/RMSw

(3)

(4)

式中：RMS為均方根值;RMSw為加權均方根值;Ratio為均方根值與加權均方根值的比值，下文簡稱均方比值;W為ISO 2631中給定的加權函數;Pa為信號的功率譜密度。

1.2 人群作用下樓板的振動響應

為了簡化分析，本文通過單人在樓板上原地踏步推導出樓板在單人作用下的振動響應模型，經過等效人群系數放大得到人群作用下的結構振動響應。

單人在樓板上任意一點原地踏步引起(x0,y0)處的穩態響應為[5]

(5)

瞬態響應為

(6)

式中：n為樓板的振型階數;i為人行荷載階數;μr,n為(x0,y0)處的第n階樓板的振型系數;μe,n為單人作用位置的振型系數;ωp為行人行走基頻對應的圓頻率;ωn為第n階結構自振圓頻率;Mn為第n階結構質量;G為行人體重;αi為動荷載因子。

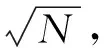
則N個人在樓板上原地踏步引起樓板在(x0,y0)處的穩態響應為

(7)

瞬態響應為

(8)

結構總響應為

1.3 人群作用下樓板振動響應均方根值

為了得到結構加速度響應的均方根值和加權均方根值，分別求取結構穩態響應和瞬態響應所對應的功率譜函數。理想情況下,穩態響應在頻率iωp/2π對應有功率譜密度值，瞬態響應在頻率為ωn/2π處對應有功率譜密度值。

穩態響應每階行人步頻對應的功率譜密度為[6]

(9)

瞬態響應每階模態頻率對應的功率譜密度為

(10)

式中:T為采樣時長，cosh函數的計算公式為

cosh(a)=(ea+e-a)/2，fn=ωn/2π，

fp=ωp/2π

人群荷載引起的結構振動響應加速度均方根值為

(11)

人群荷載引起的結構振動響應加速度加權均方根值為

(12)

均方根值和加權均方根值的比值為

(13)

由式(13)可以看出，均方比值不受人體重量、人數、分布的影響，表達式中只有Wi與人行走的頻率有關，但是根據現有研究[7]，人行走的頻率的分布比較集中，一般僅考慮與步行荷載頻率接近的單個模態的振動[8],對應的加權系數的波動不大，而且結構瞬態振動的響應比較大,Wi對總體結果產生的影響較小。下面將通過有限元模擬和現場試驗來證明上述結論。

2 人致樓板振動響應有限元模擬

通過進行有限元模擬的方式進一步驗證均方根值的性質，建立四面簡支的不同厚度樓板模型，并施加不同密度和分布的考慮人群密度和行走頻率相關的人群荷載，得到樓板振動響應信號，求取響應信號的均方比值，并對不同人群和樓板工況下的均方比值分布規律進行探討。

2.1 人群行走荷載模型與樓板模型

人群在樓板上行走的時候，可以簡化為多個單人豎向步行力荷載在樓板上連續的作用，本文通過有限元模擬建立了不同厚度的樓板，并施加了考慮人群密度與步行力參數隨機性的多種人群行走荷載，得到了不同工況下測點處的樓板加速度振動響應，并進行了均方比值分析。

單人行走豎向荷載可表示為

φi)

(14)

式中:G為人體重量,N;αi為第i階諧波的傅里葉系數;fp為人體行走頻率,Hz;φi為第i階諧波相位角;n為荷載的總諧波數。

步頻與步行速度的關系為[9]

v=0.175-0.057 5fp+0.349f2p

(15)

考慮人群密度的人群行走速度表達式為[10]

(16)

受人群密度影響的行走步頻計算公式為

(17)

將這些參數代入式(14)，即得到不同行人密度下人群步行力表達式。

建立如圖1所示樓板模型，樓板的尺寸是6 m×6 m，通過改變厚度來改變樓板的剛度。將樓板均勻的分為四個區域，在每個區域中心設置一個觀測點，樓板四面簡支[12]。人群工況P-A-B中，A代表人群行走密度，B代表人群在樓板上的分布區域，具體設置如表1所示。

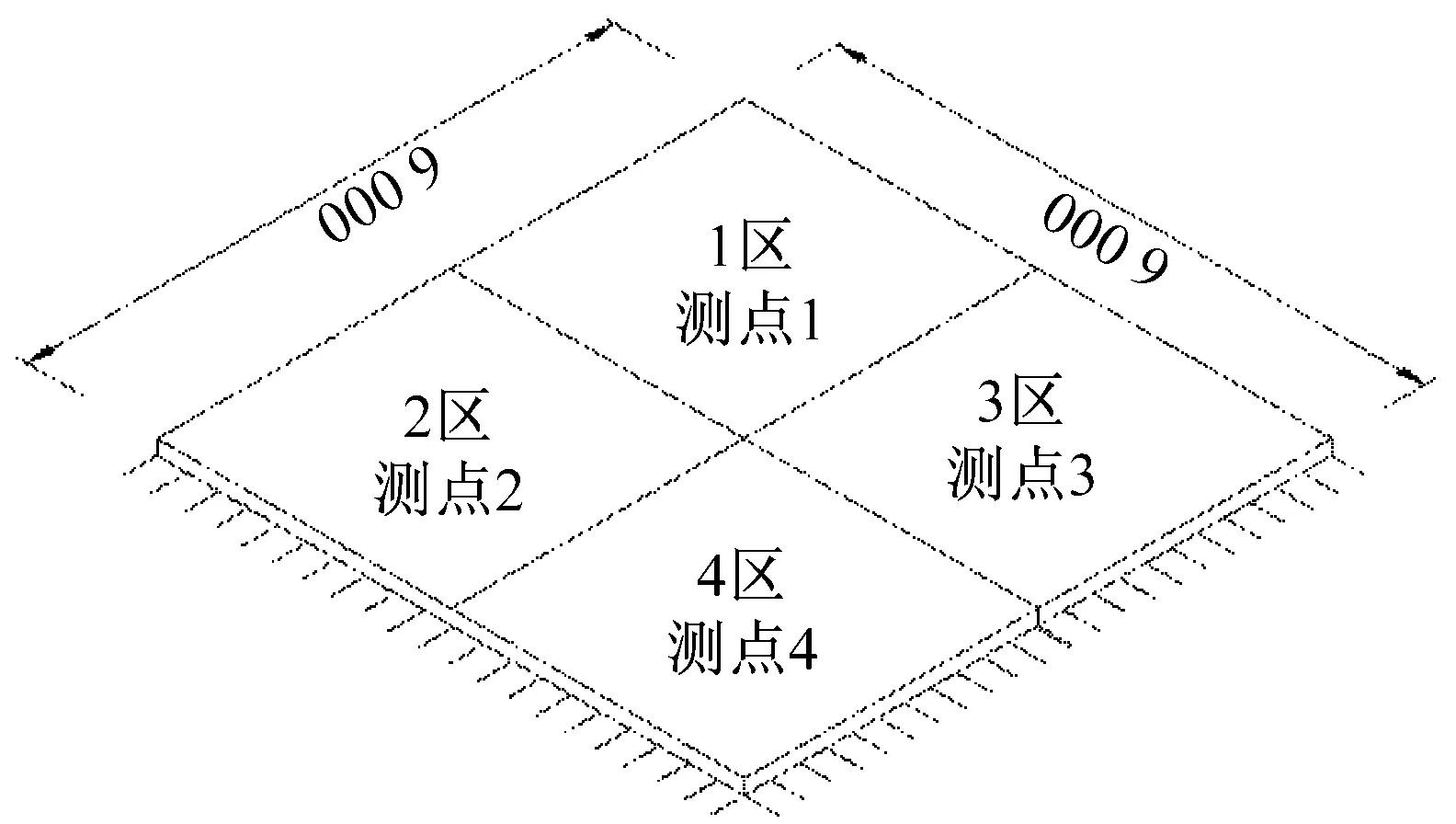
圖1 模擬樓板及分區

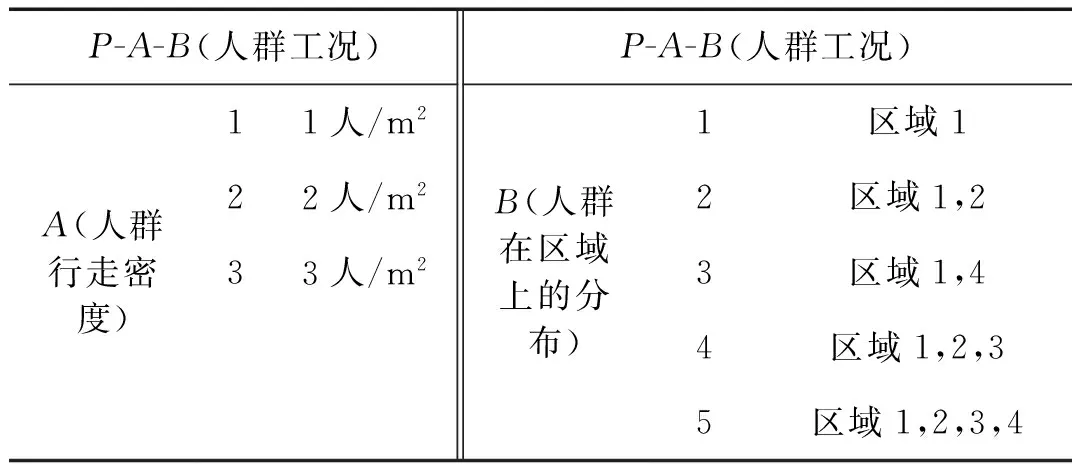
P-A-B(人群工況)P-A-B(人群工況)A(人群行走密度)11人/m222人/m233人/m2B(人群在區域上的分布)1區域12區域1,23區域1,44區域1,2,35區域1,2,3,4

樓板的厚度考慮兩種：F1代表100 mm厚的板，F2代表150 mm厚的板。樓板的彈性模量取40 GPa，泊松比取0.269，密度取2 000 kg/m3，采用Abaqus殼單元建立樓板模型，通過模態動力學分析模塊來進行動力分析，進行動力分析時考慮結構的前20階振型，樓板的阻尼比設為5%，在人群步行力作用下，采集四個觀測點位置處的振動加速度，采樣頻率為128 Hz，采樣時長為10 min。

樓板的前3階自振頻率如表2所示。

2.2 有限元模擬結果分析

計算了兩種厚度的樓板各15種人群行走工況下的均方比值，計算結果如圖2所示。

統計每種樓板每個測點在15種不同的人群工況下計算得到的均方比值的變異系數如表3所示。

表2兩種樓板的前3階自振頻率

Tab.2Thefirstthreenaturalfrequenciesofthetwokindsoffloor

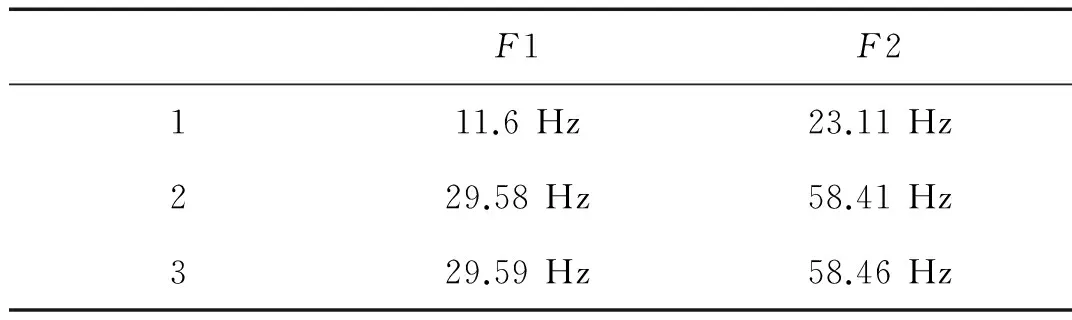
F1F2111.6Hz23.11Hz229.58Hz58.41Hz329.59Hz58.46Hz

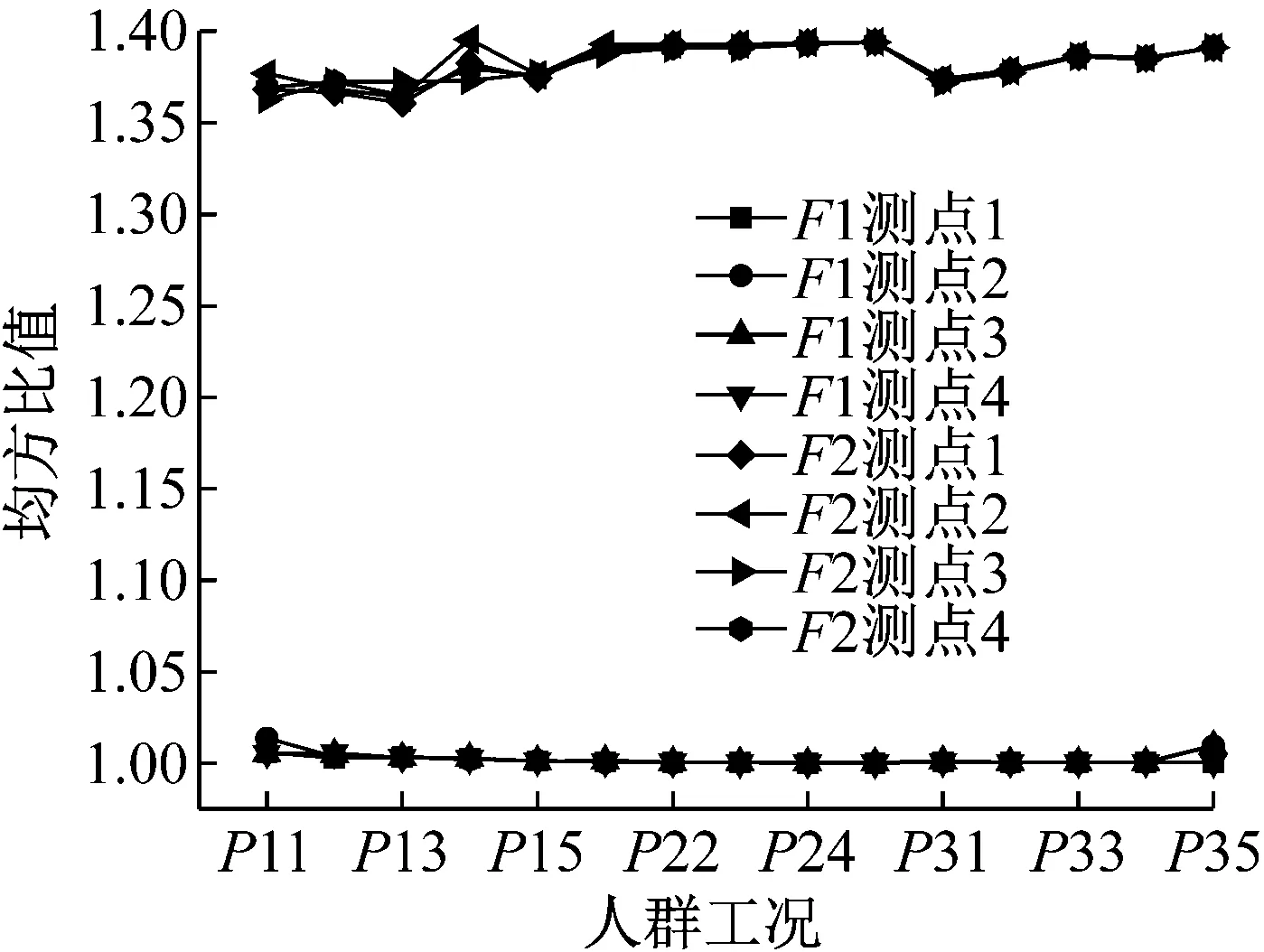
圖2 各個人群工況下樓板振動響應的均方比值

Fig.2 Ratio of the RMS of each floor vibration response of the different crowd cases

表3各個測點在不同人群工況下樓板振動響應的均方比值的變異系數

Tab.3Thecoefficientofvariationofeachsensorindifferentcrowdcases

F1F2測點12341234變異系數/%0.1590.3760.2560.1771.3111.3901.7911.487

如圖2和表3所示，每種樓板的各個測點在不同人群工況下的均方比值的變異系數很小，兩種厚度的樓板之間的均方根值差異較大，同一種厚度的樓板上的四個測點的均方根值差異較小。

有限元模擬的結果表明，結構振動響應的均方比值，受樓板自身振動特性的影響較大，基本不受作用在結構上的人群特性的影響。因此，在人群正常行走狀況下，同一個測點處測得的結構振動響應的均方比值應為一個定值，但考慮到實際信號采集過程中噪音以及其他人群行為的干擾，以及后續分析時的計算誤差等因素，實際計算出來的結構振動均方比值應在這個值上下微小浮動。

3 人致樓板振動響應實驗

理論推導和有限元模擬得到的振動響應均方比值的分析，都是理想狀況下的簡化結果，本文根據在某典型藏式古建木結構回廊處樓板進行的現場實驗，對實驗結果進行了均方比值分析，得到了在真實狀態中人群作用下樓板振動響應及其均方比值[13]。

3.1 人群荷載現場試驗

實驗區域為五跨樓板，加載區域如圖3所示，加速度計測點布置見圖4，在CZ1，CZ2，CZ5，CZ8，中底部各布置一個豎向加速度計,共計加速度計四個，并定義多種行走工況和跑步工況。

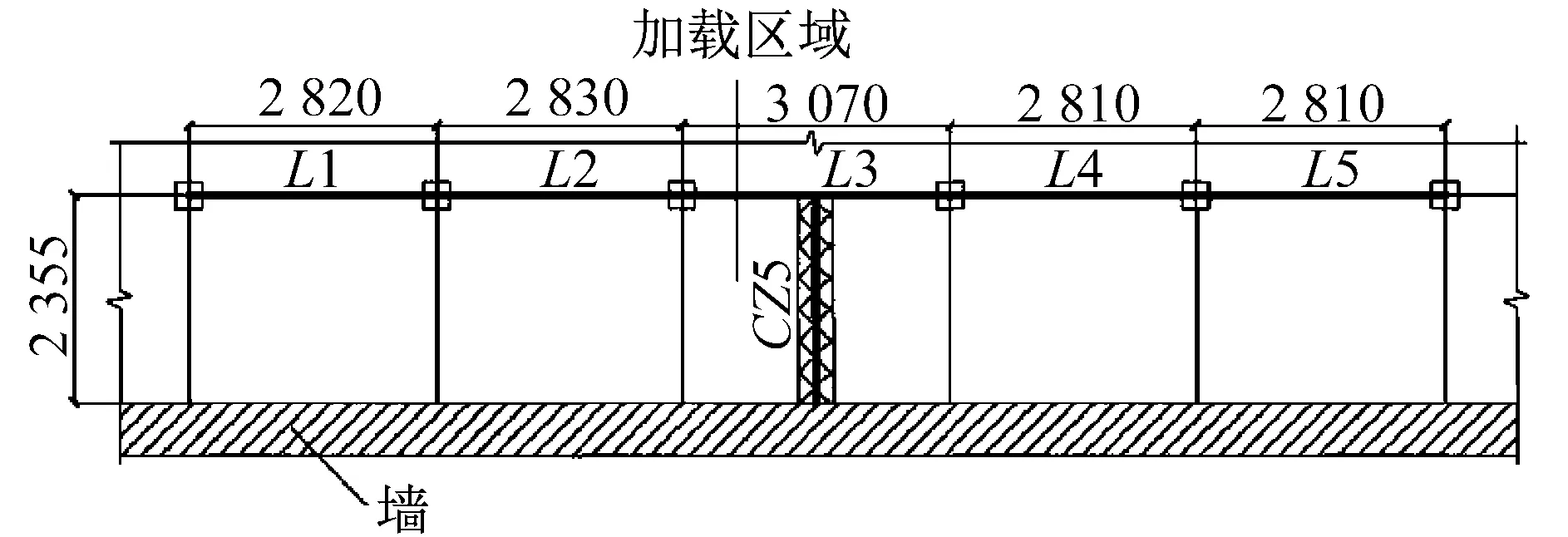
圖3 加載區域(L1～L5)

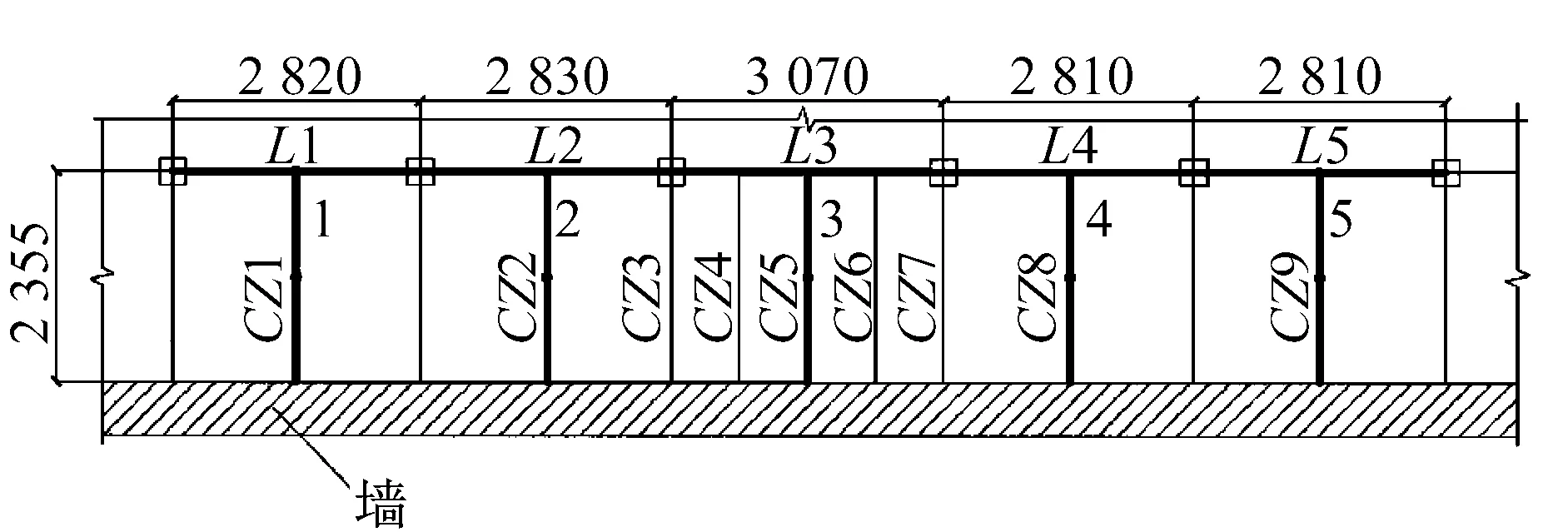
圖4 測點布置(1～4)

工況WA-B-C表示人群行走工況，工況RA-B-C表示人群跑步工況，A代表人群分布的區域，B代表人群分布的密度，C代表人群行走/跑步的頻率(見表4、表5)。

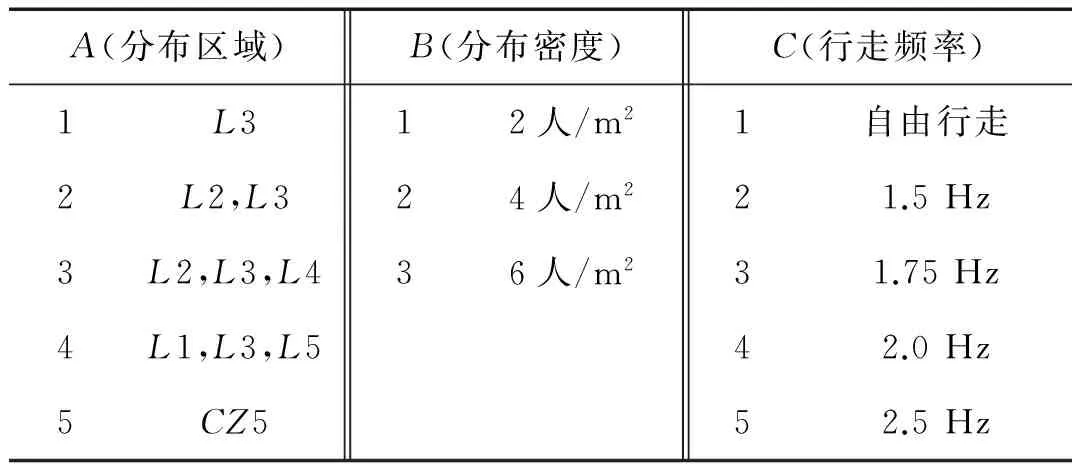
表4 人群行走工況

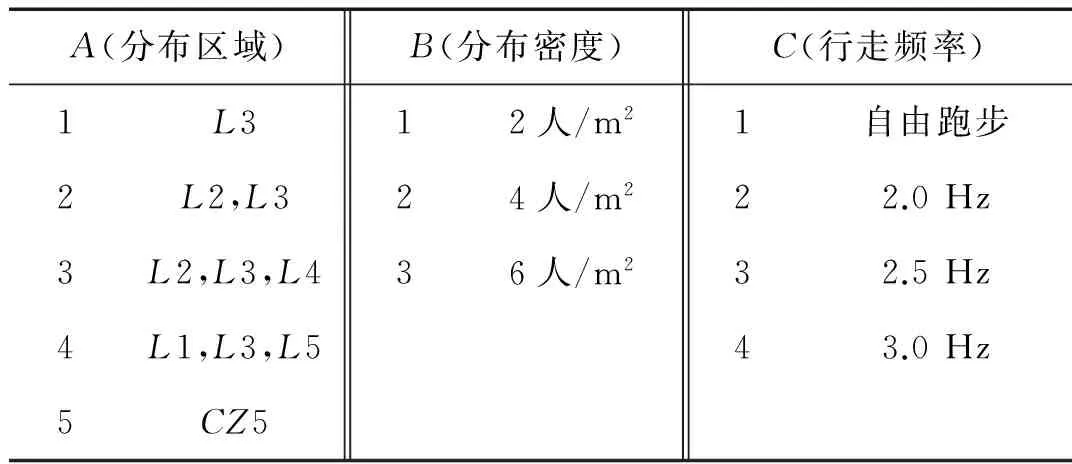
表5 人群跑步工況

表4和表5中：1/3稀疏人群(2人/m2)、2/3稀疏人群(4人/m2)、密集人群(6人/m2)。

由于行走和跑步在人致荷載施加方式上有本質上的差別，因此分別進行討論。

采用ISO規定的加權函數，計算每個測點在不同工況下的均方根值、加權均方根值及其比值。計算結果如圖5和圖6所示。

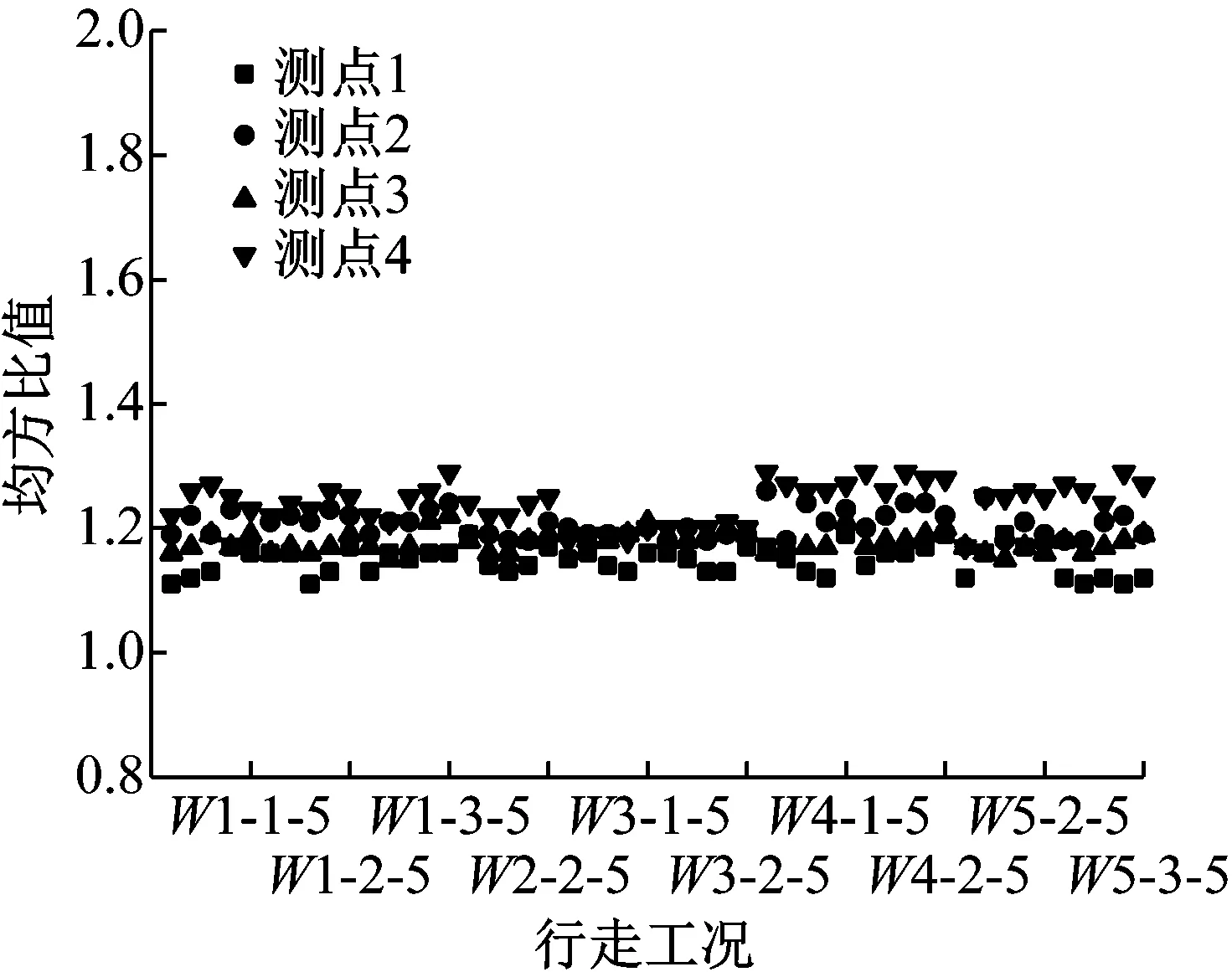
圖5 行走工況下各個測點均方比值

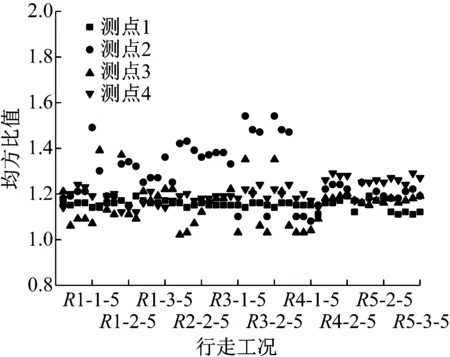
圖6 跑步工況下各個測點均方比值

由于試驗是在嚴格的監控下完成的，在試驗工程中，時刻監視著實驗者的動作是否是正常的行走動作或者跑步動作，并時刻關注著信號采集器收集到的振動信號，確保試驗過程中不產生任何的信號突變和信號漂移。因此可以認為，本次試驗采集到的結構響應信號都是由人致荷載引起的結構振動響應的真實反映。

3.2 均方比值合理分布區間確定

為了得到結構測點處均方比值分布的合理區間，先假設每個測點在不同人群工況下的實測均方比值服從正態分布，通過Kolmogorov-Smirnov檢驗，來檢測均方比值是否服從正態分布。檢驗中，顯著性水平α取0.05，h=0時表示在0.05的顯著性水平下，數據服從正態分布，h=1時表示在0.05的顯著性水平下拒絕該假設。p為該假設成立的概率。

檢驗的結果如表6和表7所示。

如表7所示，每個測點在不同人群工況下的實測均方比值服從正態分布。因此，我們可以根據各個測點處均方比值的分布來確定測點合理的均方比值分布區間,如表8所示。

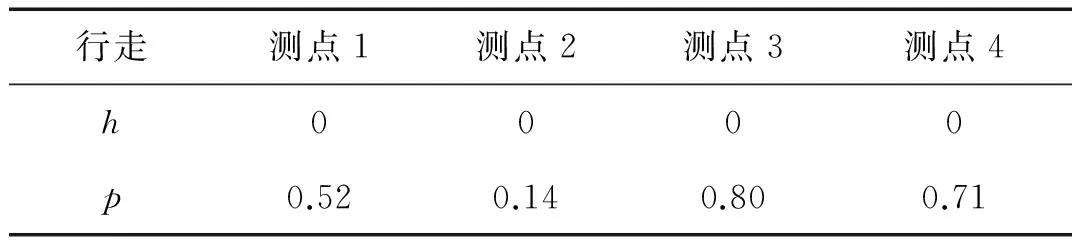
表6 行走工況下各個測點KS檢驗

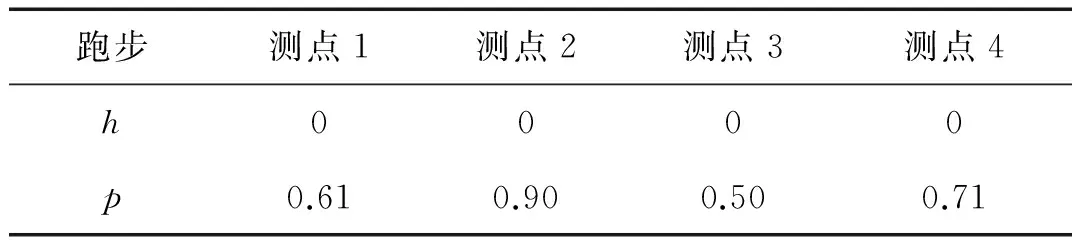
表7 跑步工況下各個測點KS檢驗

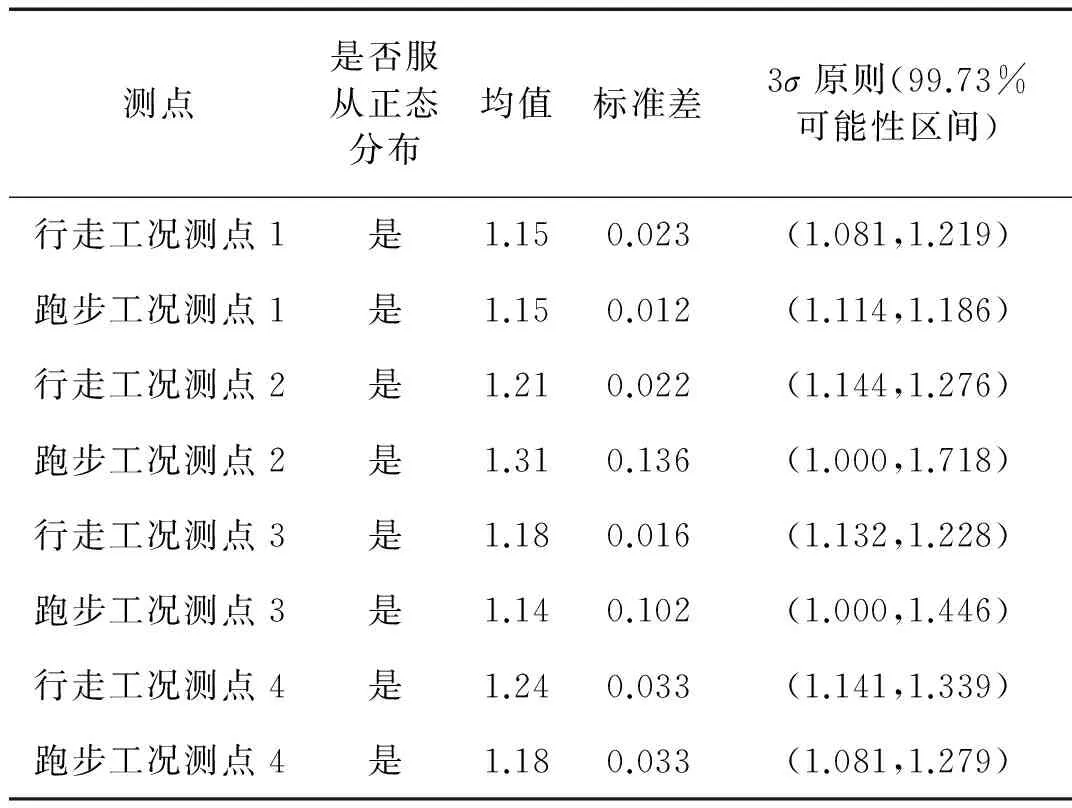
表8 人群行走試驗測點處均方比值區間

試驗中，設計了比較多的行走和跑步工況，可以涵蓋絕大多數情況下，游客在該建筑參觀時的真實行走情況，因此，根據試驗結果計算出的各個測點處的均方比值可以代表游客正常參觀時的振動響應均方比值。

然而在真實的長期監測中，無法向試驗中一樣，保證長期監測中采集到的每一條信號都是由人群引起的結構振動真實響應。在進行后續的振動分析評估中，為了快速篩選出有效的振動信號，可以用試驗中根據3σ原則計算出的每個測點處均方比值的合理區間對結構長期監測中信號進行篩選。

在確定測點處均方比值的分布區間后，對于該測點處監測到的加速度信號，如果該信號的均方比值在這個區間內，那么可以認為該信號是由人群的正常行為引起的，是監測到的有效信號，可以用該信號進行后續的振動分析和評價；如果監測到的信號的均方比值不在該區間內，則認為該信號是無效信號，不能用來進行后續的振動評價。即用該分布區間作為信號評價和篩選的標準。

4 結 論

本文提出了一種新的衡量人致樓板振動響應信號的參數，該參數是振動信號的均方根值和加權均方根值的比值，通過理論分析和有限元模擬對這個比值的性質進行了探討，并通過現場試驗和長期監測的數據驗證了參數的性質。主要結論如下：

(1) 結構同一位置在人群荷載作用下加速度數據的加權和未加權均方根值的比值，受人群數量，行走頻率和分布情況的影響較小，這個比值的數值，與測點處的結構形式、連接方式、材料等結構的本身性質有關。

(2) 通過現場的人群行走實驗可以確定關鍵位置的均方比值的合理分布范圍，對于該測點處采集到的人致振動響應監測數據，超出這個范圍的數據視為異常數據，應該剔除。該參數為篩選人群荷載作用下結構加速度響應數據提供了一定依據。

(3) 均方比值還可以用來區分不同頻段的激勵引起的振動響應。對于同一結構，不同頻段的激勵引起的振動響應的均方根值分布于不同的區域，可以通過均方比值的差別來區分不同激勵引起的響應信號。

(4) 該方法主要可以應用在人致振動長期監測中，大量振動信號的批量處理，可以通過簡單的人致振動試驗或者一部分長期監測信號確定結構人致振動均方比值的范圍，通過這個范圍可以對非人群荷載引起的振動信號進行快速批量剔除。可以提高工作效率以及振動評估的有效性。

[1] ANTONI J，RANDALL R B. Unsupervised noise cancellation for vibration signals: Part I-evaluation of adaptive algorithms[J]. Mechanical Systems and Signal Processing，2004，18(1): 89-101.

[2] 肖立波, 任建亭, 楊海峰. 振動信號預處理方法研究及其MATLAB實現[J]. 計算機仿真, 2010, 27(8):330-333.

XIAO Libo, REN Jianting, YANG Haifeng. Study on vibration signal pre-processing method based on MATLAB[J]. Computer Simulation, 2010, 27(8):330-333.

[3] 李舜酩, 郭海東, 李殿榮. 振動信號處理方法綜述[J]. 儀器儀表學報, 2013, 34(8):1907-1915.

LI Shunming, GUO Haidong, LI Dianrong. Review of vibration signal processing methods[J]. Chinese Journal of Scientific Instrument, 2013, 34(8):1907-1915.

[4] 賴素建, 靳曉雄, 彭為,等. 信號預處理中錯點剔除方法的研究[J]. 佳木斯大學學報(自然科學版), 2011, 29(3):333-336.

LAI Sujian, JIN Xiaoxiong, PENG Wei, et al. Research on the method to reject abnormal data in signal preprocessing[J]. Journal of Jiamusi University(Natural Science), 2011, 29(3):333-336.

[5] 潘寧. 人行荷載下樓板振動響應舒適度研究[D]. 北京:中國建筑科學研究院, 2012.

[6] 歐進萍. 結構隨機振動[M]. 北京:高等教育出版社, 1998.

[7] Mechanical vibration and shock-evaluation of human exposure to whole-body vibration—Part 1: general requirements: ISO 2631-1[S].[S.l.]: International Organication for Standardization，1997.

[8] 法永生, 李東, 孫翠華. 人行橋隨機人行荷載下的振動分析及其舒適度評價的新方法[J]. 振動與沖擊, 2008, 27(1):119-123.

FA Yongsheng, LI Dong, SUN Cuihua. A new method of vibration analysis and evaluation of comfortableness of footbridge under random pedestrian load[J]. Journal of Vibration and Shock, 2008, 27(1):119-123.

[9] BERTRAM J E A, RUINA A. Multiple walking speed-frequency relations are predicted by constrained optimization[J]. Journal of Theoretical Biology, 2001, 209(4): 445-453.

[10] VENUTI F,BRUNO L. An interpretative model of the pedestrian fundamental relation[J]. Comptes Rendus Mecanique,2007,335(4): 194-200.

[11] ZIVANOVIC S, PAVIC A, REYNOLDS P. Probability-based prediction of multi-mode vibration response to walking excitation[J]. Engineering Structures, 2007,29(6): 942-954.

[12] 陳雋, 葉艇, 彭怡欣. 行走激勵下樓蓋振動加速度反應譜研究[J]. 振動與沖擊, 2014, 33(24):1-7.

CHEN Jun, YE Ting, PENG Yixin. Acceleration responses pectrum of a long span floor under human walking load[J]. Journal of Vibration and Shock, 2014, 33(24):1-7.

[13] 郭婷. 藏式古建結構的人致荷載分析[D]. 北京:北京交通大學, 2009.