城市快速路交織區通行能力分析與仿真

寧波工程學院 浙江 寧波 315031

正文：

0 引言

沿著相當長的路段行駛的兩股或多股基本平行的同向交通流，不借助于交通控制設施運行，定義為交織。并且交織區交通流特性對于公路以及城市快速路合流以及分流區域的瓶頸消除有著至關重要的作用。其具體概念為當道路由合流區入口、輔助車道、分流區出口緊密相接時，或者當一條駛入匝道、一段輔助車道、一條駛出匝道緊密連接時，這兩種構成形式就形成了交織區。

由于交織區較基本路段相比較復雜，影響其通行能力因素眾多，以1950年美國《通行能力手冊》的發布拉開了學者們研究交織區的帷幕。HCM2000將交織區構型分成A、B、C三類，給出了在交織區構型、長度、車道數和流量比在不同情況下組合時的通行能力值。Lertworawanich等利用線性規劃理論來求解交織區通行能力。我國交通部門將交織區分成Ⅰ類、Ⅱ類、Ⅲ類，通過各種因素對交織區運行特性的影響分析，建立了其通行能力模型。任荔娜根據城市快速路車輛的動態運行規律，得到了交織區內車輛的行為特征及交通流特性，并依據此特征建立了基于元胞自動機的城市快速路交織區跟馳模型及換道模型。蔡雯娟通過定性和定量相結合的方法，分析交織區各個參數的分布規律并建立VISSIM模型，最終推算出設計車速為80km/h時的符合我國西安市駕駛員特征的城市快速路A類三車道交織區通行能力計算公式。

若直接采用實地調查的方式來建立模型，則需要大量的人力物力投入，且受到資金、技術等限制，而在模擬仿真中，交通流參數都是人為輸入設定，有時得出的結論與實際背道而馳。因而，本文利用VISSIM模型對交織路段進行仿真實驗，將理論模型所得出的數據與部分實測數據相結合，通過改變其輸入條件，將各種情況排列組合，得出在不同情況下的通行能力值，確立交織區通行能力模型，最后用寧波市區機場南路交織路段驗證此模型的準確性。

1 交織區通行能力影響因素

交織區在道路通行系統中占有重要地位，本文主要研究交織長度，交織車道數，交織區構型，交織流量比四個因素對通行能力的影響。

1.1 交織區長度

主路與匝道車輛在行駛過程交匯并變換一次車道行駛的距離稱為交織區長度。HCM2000認為，高速公路一般交織區長度應該在750m以下，由于其車輛類型以及屬性、行車類型均不同，所有城市快速路限速和長度一般低于高速公路。本文所研究的交織區長度為500m，對大多數城市快速路交織區來說，此長度下的通行能力較有借鑒意義。

1.2 交織車道數

交織車道數，即交織區段內的車道數，是供車輛完成交織行為的附加車道，一般用N表示。A類交織區中能被交織車輛使用的最大車道數是受限制的，每輛車最多使用車道數約為1.4個車道。我們一般都用車道數來衡量一條道路的通行能力，通常在其他影響因素都適宜的條件下，車道數越多代表通行能力越強，所以交織車道數可以作為影響交織區通行能力的一個重要影響因素。

1.3 交織區構型

交織區構型主要有A、B、C三類，A類交織區中兩個交織方向的所有車輛均進行一次變換車道行為;B類交織區是最主要的交織構型，可以有效承載較大交織交通量；C類交織區與B類較為相似，僅較于B類多一條直通車道。本文主要討論了A類交織區構型的通行能力。

1.4 交織流量比

交織流量比為交織流量與總交通量的比值。車輛在交織區中運行過程中存在交織行為，導致交織區內交通流車頭時距增加，導致交織區通行能力會比一般路段的通行能力小。因此，交織流量比是影響交織區通行能力的重要因素，有著舉足輕重的地位。

2 確定交織區通行能力模型

2.1 確定模型

由于城市快速路交織區長度大多均為500m，為了得出交織流量比與交織通行能力的關系，根據通行能力與交織區流量比的關系，采用當交織流量比為0.2、0.25、0.3、0.35、0.4時500米A類交織通行能力，并做出如下假設模型：

其中：C-----交織區通行能力

r-----交織流量比

a，b，d-----標定參數

3.利用VISSIM仿真

本節利用基于Vissim搭建的仿真平臺，構建通用A型交織區仿真路網進行仿真；在城市快速路交織區通行特性的基礎上標定仿真參數；基于以上兩點來得出仿真結果再由matlab進行數據趨勢擬合，與理論的模型進行對比分析，驗證理論模型的正確性。

3.1 仿真背景介紹

選取A類快速路交織區一般典型路段作為仿真實驗路段，該路段有一個交織區，由一個入口匝道和一個出口匝道構成，如圖3-1所示。該實驗路段交織區設定車道數為變量，主入進口車道數從兩車道開始變化，入口匝道與出口匝道數從單車道開始變化，實驗交織區長度作為變量將設置200米到500米作為變化范圍。

圖3-1 A類交織區仿真路網

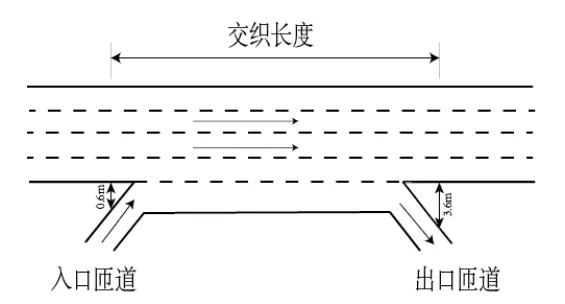
圖3-2 交織區路段示意圖

3.2 仿真軟件參數標定

1.仿真參數設置：本次仿真時間設置為1h，所以將VISSIM中仿真參數設置為3600仿真秒，考慮實際條件，將仿真精度設置為5，根據仿真經驗將隨機種子設置為42。

2.駕駛行為參數設置：①由于快速路交織區比其他路段更易發生交通問題，交通沖突較其他路段更多，所以應該將駕駛人的最大前視距離設置應由原本的250米增加到257米。②由于快速路交織區的車道變換相比于其他路段更加復雜，在VISSIM軟件內不加設置會導致車輛集中堵在下半段區域，所以需要對車輛車道變換模型進行修正，具體設置結果如圖3-3所示。

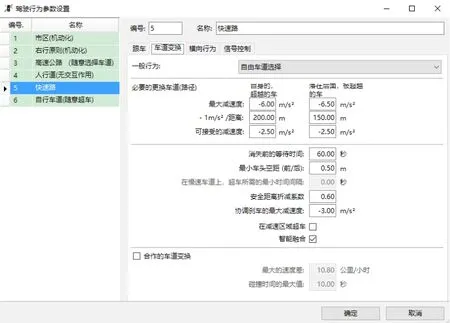
圖3-3 車道變換模型修正

3.變道位置設置：在輸入車輛后，經過多次仿真，發現未經設置時的車輛變道常發生在交織區下半部分（如圖3-4所示），與實際不符，實際調查中車輛變換應該大都發生在交織區前半段所以應該對車道變換距離進行更改。本次仿真將交織區下游的路段連接器的車道變換距離均修改為250m，緊急停車距離修改為10m。

圖3-4 初始仿真交織區變道位置圖

經過以上參數標定后，雖然無法做到與實際完全等同，但是比之前更加接近與實際情況，更加真實，使得車輛變道更合理有序。

3.3 仿真數據標定系數

在2、3、4車道情況下分別進行五組不同交織流量比的仿真，并得出相應的15組通行能力數據（如表3-1所示），將數據用于模型的系數標定，得出相應的系數。將上表數據引入模型，并標定系數：

表3-1不同交織流量比對應通行能力數據

其中：C —— 交織區通行能力

r —— 交織流量比

3.4 實測數據檢驗

根據寧波市機場路夏禹路立交北側的快速路交織區來驗證模型的適用性，其長度約500m，交織流量比2.5：7.5，車道數為3，并將這些參數輸入通行能力計算模型，可得通行能力計算結果為3993pcu/h，實際觀測值與模型得出的通行能力相差不超過5%，因此此通行能力計算模型是有適用性的。

4.結論

本文以典型A類快速路交織區為例，基于假定模型，運用Vissim軟件進行快速路交織區的仿真模擬，得到快速路交織區的通行能力并進行分析，得到如下結論：

(1)通過假設交織區通行能力模型，通過VISSIM仿真進行參數標定，分別得到2、3、4車道數下的三種通行能力模型，該模型能更好的模擬實際的交通狀況。

(2)對A類交織區進行VISSIM仿真模擬，在不同車道數下VR對該類交織區通行能力的影響進行分析。利用Matlab分別對車道數為2、3、4，交織長度為500m的情況進行擬合，獲得不同情況下的城市快速路交織區通行能力模型度。

(3)通過VISSIM仿真模擬，可以反映交織區的通行特性，通過仿真數據與實際數據相比較，認為該模型是具有一定的可行性與適用性的，擁有良好的實用價值。